INTRODUCTION
Il existe de nombreux sites très complets expliquant le fonctionnement d’une montre mécanique. Toutefois, malgré des efforts de vulgarisation méritants, beaucoup d’explications nécessitent un prérequis que n’ont pas forcément ceux qui abordent le sujet depuis peu. Une raison possible est que les explications ont tendance à s’appuyer sur des mécanismes existants sans forcément exposer pourquoi ces mécanismes ont été conçus ainsi.
Les explications données ici proposent une autre approche : supposons que nous souhaitions concevoir une montre mécanique à aiguille (analogique) simple. Comment faudrait-il procéder ?
Je parle bien de conception et pas de fabrication qui est un problème autrement complexe.
SUIVI DE VERSIONS
- Version 1.0, 2019 : version initiale.
- Version 1.1, 2022 : correction d'une erreur de calcul suite au signalement d'un internaute (variation sur une journée pour 1ms de décalage).
- Version 1.2, 2023 : réglage des mouvements de Paris avec un chronocomparateur.
- Version 1.3, 2023 : ajout du chronocomparateur PC-RM5.
PRINCIPES GENERAUX
Exposé du problème
On souhaite concevoir une montre destinée à être portée au poignet (donc, devant fonctionner dans toutes les positions et soumise à des accélérations), comportant une aiguille pour marquer les secondes (60 secondes en un tour d’aiguille), une autre pour les minutes (60 minutes pour un tour d’aiguille) et une autre pour les heures (12 heures pour un tour d’aiguille).
Afin de limiter les choix de conception, on prendra comme contrainte de faire fonctionner la montre à l’aide d’engrenages.
On adoptera également dans un premier temps une hypothèse simplificatrice dans laquelle les engrenages fonctionnent sans frottement.
Rappel sur les engrenages
Les engrenages ont cette merveilleuse faculté de pouvoir réduire ou multiplier la vitesse de rotation.
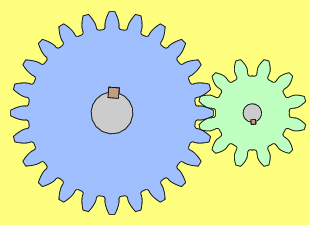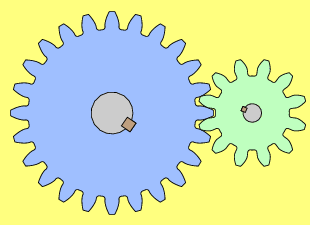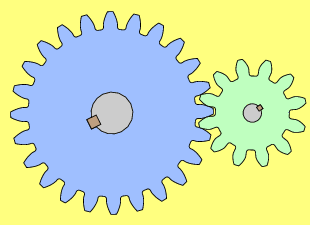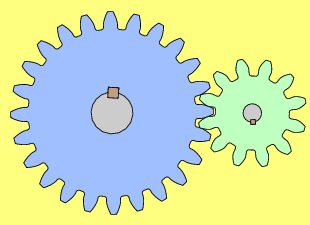
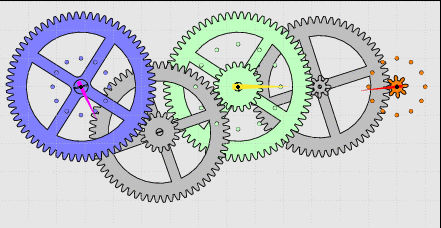
On appelle « engrenage d’entrée » (par exemple, le bleu dans l'animation ci-après), l’engrenage qui impulse une certaine rotation à une vitesse Ve et « engrenage de sortie » (par exemple, le vert dans l'animation ci-après), l’engrenage qui restitue une certaine rotation à une vitesse Vs.
On notera K, le rapport entre Ve et Vs : Vs = K x Ve
Si K est supérieur à 1, Vs sera plus grande que Ve d’un facteur K. L’engrenage de sortie tournera plus vite que l’engrenage d’entrée.
Si K est inférieur à 1, Vs sera plus faible que Ve d’un facteur K. L’engrenage de sortie tournera moins vite que l’engrenage d’entrée.
On montre que K = [Nombre de dents de l'engrenage d'entrée]/[Nombre de dents de l'engrenage de sortie]
Ainsi, si l’engrenage d’entrée comporte 10 dents et celui de sortie 100 dents, K = 10/100 = 1/10.
Donc Vs = K x Ve = 1/10 x Ve : l’engrenage de sortie ira 10 fois moins vite que l’engrenage d’entrée ou dit autrement, il faudra 10 tours de l’engrenage d’entrée pour que l’engrenage de sortie fasse 1 tour.
Si l’on inverse l’engrenage d’entrée et l’engrenage de sortie, on aura donc un engrenage d’entrée qui comportera 100 dents et un engrenage de sortie qui comportera 10 dents donc K = 100/10 = 10
Donc Vs = K x Ve = 10 x Ve : l’engrenage de sortie ira 10 fois plus vite que l’engrenage d’entrée ou dit autrement, lorsque l’engrenage d’entrée aura fait 1 tour, l’engrenage de sortie aura fait 10 tours.
On notera que le sens de rotation de l’engrenage de sortie sera inversé par rapport à l’engrenage d’entrée.
Pour connaitre le sens de rotation d’un engrenage de sortie lorsqu’on passe par une succession d’engrenages, il suffit de compter le nombre d’axes d’engrenages : s’il est pair (2, 4, 6…), l’engrenage de sortie tournera dans le sens inverse de l’engrenage d’entrée. S’il est impair (1, 3, 5, 7…), il tournera dans le même sens.
Aiguille des secondes et aiguille des minutes
Supposons que nous soyons en mesure de lancer une roue qui supporte l’aiguille des secondes à une vitesse telle qu’elle fasse un tour par minute. Puisque par hypothèse, il n’y a pas de frottement, cette aiguille tournera indéfiniment et fera toujours un tour par minute.
Nous souhaitons maintenant que lorsque cette aiguille a fait un tour (60 secondes), l’aiguille des minutes ait avancé d’une minute. Lorsque l’aiguille des secondes aura fait 60 tours (3600 secondes), l’aiguille des minutes aura donc avancé de 60 minutes soit une heure.
Mettons un engrenage (engrenage d’entrée) comportant, par exemple, 10 dents, sur la roue qui supporte les secondes. Mettons également un engrenage (engrenage de sortie) qui comporte 600 dents sur la roue qui supporte l’aiguille des minutes et qui est actionné par l’engrenage associé aux secondes.
Lorsque l’aiguille des secondes aura fait un tour complet (60 secondes), les 10 dents de l’engrenage associé aura également fait un tour complet.
Quant à l’engrenage associé aux minutes, il aura effectué :
K = 10/600 de tour soit 1/60 : l’aiguille des minutes aura donc avancé d’une minute mais dans le sens inverse de l’aiguille des secondes (nombre d’axes pair). Dans cet exemple, K vaut donc 1/60.
Ou encore, lorsque l’aiguille des secondes aura fait 60 tours, l’aiguille des minutes aura fait 60 x K = 60 x 1/60 = 60/60 = 1 tour.
Elle aura donc avancé de 60 minutes (1 tour) soit une heure, ce que l’on souhaite, mais toujours dans le sens inverse de l’aiguille des secondes.
Évidemment, avec cette approche, il y a au moins un problème, en plus de celui lié à l’inversion de sens : Faire un engrenage qui comporte 600 dents n’est pas simple et même si l’on ne s’occupe pas ici de construction, on se doute que ça prendra de la place dans une montre à porter au poignet.
La solution évidente est d’introduire un engrenage intermédiaire entre celui des secondes et celui des minutes ce qui permettra de faire tourner l’aiguille des minutes dans le même sens que l’aiguille des secondes (nombre d’axes impair). Et si l’on s’y prend bien, le nombre de dents de l’engrenage des minutes et de l’engrenage intermédiaire deviendra beaucoup plus raisonnable.
Pour alléger l’écriture, appelons ESec, l’engrenage des secondes, ESecMin, l’engrenage intermédiaire entre celui des secondes et celui des minutes et EMin, l’engrenage des minutes. Dans le même ordre d’idée pour la suite, on appellera EMinHeure l’engrenage intermédiaire entre celui des minutes et celui des heures et EHeure, l’engrenage des heures.
Sans faire spécialement un calcul, posons qu’ESecMin ait 60 dents.
K1 (le facteur K entre ESec et ESecMin) vaut donc 10/60 = 1/6 (réduction 1/6) : lorsqu’ESec qui a 10 dents aura fait un tour (donc 60 secondes), ESecMin aura fait 1x10/60 = 1/6 de tour mais dans le sens inverse d’ESec puisqu’il y a un nombre pair d’axes.
On veut que lorsqu’ESec aura fait 60 tours, EMin fasse un tour. Il nous faut donc maintenant calculer le coefficient K2 entre ESecMin et EMin.
Lorsqu’ESec fait 60 tours, ESecMin fait 60 x 1/6 de tours soit 60/6 = 10 tours.
Donc, lorsqu’ESecMin fait 10 tours (60 minutes), EMin doit faire 1 tour.
Associons un engrenage de 10 dents à ESecMin, cet engrenage étant solidaire de l’engrenage de 60 dents.
On veut que [nombre de tours d’ESecMin = 10] x [Nombre de dents = 10] / [Nombre de dents d’EMin] = 1 => Nombre de dents d’EMin = 100 et K2 est égal à 10/100 = 1/10 (réduction d’1/10).
Lorsque l’engrenage de 10 dents d’ESecMin aura fait 10 tours, EMin aura bien fait 1 tour et cette fois ci, dans le sens d’ESec puisque le nombre d’axe est impair.
Réaliser des engrenages de 60 dents ou 100 dents est plus raisonnable qu’un engrenage de 600 dents en termes d’encombrement.
On notera au passage que lorsqu’on a une succession d’engrenage, le facteur K global du « train d’engrenage » est égal au produit des facteurs K entre chaque paire d’engrenage.
Ainsi, dans le cas présent, KGlobal1 = K1 x K2 = 1/6 x 1/10 = 1/60. Ça semble correct : lorsqu’ESec (l’aiguille des secondes) a fait 60 tours, on veut qu’EMin (l’aiguille des minutes) fasse 1 tour !
Dans l'animation ci-dessous, ESec qui porte les secondes est le petit engrenage orange à droite, le premier engrenage gris en partant de la droite est ESecMin, l'engrenage vert qui porte les minutes est EMin.
Aiguille des minutes et aiguille des heures
Le même raisonnement s’applique entre les aiguilles des minutes supporté par EMin et celles des heures supportées par EHeure : on veut que lorsque l’aiguille des minutes fait 1 tour (60 minutes), l’aiguille des heures avance d’1/12 (1 heure sur un cadran de montre qui affiche 12 heures) et dans le même sens que l’aiguille des minutes.
Si l’on nomme K3, le facteur K entre EMin et EMinHeure et K4, le facteur K entre EMinheure et EHeure, on peut écrire que K3 x K4 = 1/12 = KGlobal2.
Pour résoudre cette équation, il nous faut fixer un des K. Posons K4 = ¼. Dans ce cas, K3 = 1/3 (1/4 x 1/3 = 1/12). On pourra prendre un engrenage de 10 dents pour l’un des engrenages d’EMinHeure et 40 dents pour EHeure. On pourra associer un engrenage de 30 dents à l’engrenage de 100 dents d’Emin et pour l’autre engrenage d’EMinHeure, mettre un engrenage de 10 dents.
KGlobal2 = K3 x K4 = (10/30) x (10/40) = (1/3) x (1/4) = 1/12
Et si l’on considère maintenant le train d’engrenage global entre les secondes et les heures, on a :
KGlobal = KGlobal1 x KGlobal2 = 1/12 x 1/60 = 1/720.
Lorsque l’aiguille des secondes fera 720 tours, l’aiguille des heures fera un tour complet. En effet, en une heure, l’aiguille des secondes a fait 60 rotations (60 mn). En 12 heures, elle doit donc faire 60 x 12 rotations soit 720 rotations.
On remarque qu’il peut y avoir plein de solutions possibles (en théorie, une infinité) pour calculer les différents facteurs K et donc déterminer les nombre de dents des différents engrenages.
En pratique, ce choix sera déterminé par la construction, c’est-à-dire, la capacité à réaliser des engrenages qui engrènent bien, ne soient pas trop grands, ne s’usent pas trop vite, etc. ce qui est une autre histoire…
Dans l'animation précédente, EMin qui porte les minutes est l'engrenage vert, EHeure qui porte les heures est l'engrenage bleu, l'engrenage gris entre les deux est EMinHeure.
Et bien voilà. Selon l’hypothèse simplificatrice où il n’y a pas de frottement, la montre est terminée. Il suffit de lancer la roue des secondes une bonne fois pour toute à la bonne vitesse et la montre marquera l’heure avec une précision qui ne dépendra que de l’impulsion initiale et ceci, pour une éternité.
Sauf que dans la réalité, il y a des frottements et qu’il va donc falloir les compenser en apportant en permanence une certaine quantité d’énergie pour entretenir le mouvement des roues qui supportent les aiguilles.
Énergie d’une montre mécanique
Pour information, le rendement de la transmission de puissance entre deux engrenages cylindriques à dentures droites comme on en trouve dans les montres est de l’ordre de 98%. Le rendement global de transmission est égal au produit des rendements entre les couples d’engrenages d’un train d’engrenage. Ce qu’il faut retenir, c’est qu’il est inférieur à 1.
Pour pallier à la perte d’énergie due aux frottements, il faudra apporter une énergie en compensation. Dans une montre mécanique, cet apport d’énergie est généralement produit par un ressort en spirale qui se trouve dans un barillet, choix de conception que nous retiendrons par la suite.
Une extrémité du ressort est solidaire de l’arbre de barillet. L’autre extrémité est fixée sur le bord intérieur de la face extérieure du barillet.
Pour tendre le ressort, on maintien fixe le barillet et on tourne l’arbre de barillet de façon à enrouler le ressort sur lui-même.
Pour détendre le ressort et fournir l’énergie à l’extérieur, on maintien fixe l’arbre de barillet et on laisse le barillet tourner sur lui-même grâce à la détente du ressort. Lorsque le ressort est détendu, le barillet s’arrête.
Pour transmettre cette énergie au reste de la montre, le barillet est lui-même un engrenage que l’on associera directement ou indirectement à l’engrenage des secondes.
En général, l’arbre de barillet comporte un axe carré sur lequel on peut fixer un engrenage. Ce dernier permet le remontage de la montre via un système de remontoir manuel ou automatique, on y reviendra. Un cliquet permet de bloquer cet engrenage, donc l'arbre de barillet dans un sens de rotation : l’arbre de barillet ne peut que tourner dans le sens du remontage. Le ressort ne peut se détendre que via le barillet qu’il fera tourner en lui transmettant son énergie.
Malheureusement, on ne sait pas produire un barillet en mesure de fournir un « couple » régulier au cours du temps.
Si on relie un barillet, dont le ressort a été préalablement tendu, au train d’engrenage que l’on a défini précédemment, on verra l’aiguille des secondes tourner rapidement (et avec elle, l’aiguille des minutes et des heures) puis de moins en moins vite au fur et à mesure que le ressort se détend, et ce, jusqu’à l’arrêt complet, l’énergie restante contenue dans le ressort n’étant plus en mesure de compenser les frottements.
On a donc une potentielle solution pour fournir de l’énergie à la montre mais à ce stade, on ne sait pas la fournir de façon régulière afin que l’aiguille des secondes avance en marquant effectivement les secondes. Il faudra donc trouver un moyen de réguler cet apport d’énergie.
Un autre point à prendre en compte est qu’en pratique, la taille du barillet ne lui permet pas de disposer d’un ressort en mesure d’emmagasiner beaucoup d’énergie. Au bout de quelques tours sur lui-même, le barillet aura délivré toute l’énergie de son ressort. Or, on souhaite qu’une montre puisse fonctionner « un certain temps » (disons, trente à quarante heures) sans que l’on ait à retendre le ressort.
Il faudra donc faire en sorte qu’une très faible rotation du barillet puisse provoquer une rotation importante de l’aiguille des secondes, (et donc des minutes et des heures).
Si par exemple, l’énergie contenue dans le barillet devient insuffisante pour mouvoir l’aiguille des secondes au bout de 5 tours et que l’on souhaite une autonomie de 40 heures, soit 2400 tours de l’aiguille des secondes (60 x 40 minutes), il faudra multiplier par 480 (2400 / 5) le mouvement du barillet.
On pourrait décider de multiplier par 960 ce qui permettrait de tenir 80 heures mais on se heurte à un autre problème : le couple transmis à travers une telle multiplication est divisé par le facteur de multiplication. En d’autre termes, si le couple a une valeur C en sortie de barillet, il aura une valeur de C / K au niveau de l’engrenage après multiplication, K étant égal au nombre de dents de l’engrenage d’entrée divisé par le nombre de dents de l’engrenage de sortie, c’est-à-dire, le facteur de multiplication ou de réduction définit précédemment. Cette relation est en fait une simplification de l’équation réelle. Elle suppose que les diamètres des engrenages sont proportionnels au nombre de dents ce qui est généralement une hypothèse vérifiée.
On remarque au passage que lorsque l’on réalise une réduction, on augmente le couple en sortie du train d’engrenages du facteur KGlobal définit précédemment (KGlobal étant dans ce cas inférieur à 1). Par contre, lorsque l’on réalise une multiplication, on diminue le couple en sortie du train d’engrenages de ce même facteur KGlobal (KGlobal étant dans ce cas supérieur à 1).
Pour conclure cette partie, on doit donc choisir un compromis entre le facteur de multiplication et le couple que l’on souhaite obtenir en fonction des frottements calculés ou constatés.
Base de temps
Puisque l’on ne dispose pas d’une source d’énergie constante et complètement maitrisée, on doit trouver un moyen pour la réguler.
On connait depuis longtemps les propriétés du pendule simple (une tige rigide de longueur l fixée sur un axe et qui supporte une masse M). Pour de petites oscillations, la période du pendule se calcule de la façon suivante :
T = 2 x π x √(l / g) où g en newton par kilogramme (N.kg−1), représente l'intensité du champ de pesanteur.
Cette propriété est utilisée dans les horloges pour réguler son mouvement et fonctionne plutôt bien même si on doit compter sur le fait qu’en pratique, l n’est pas constant en fonction de la température et g dépend de l’altitude.
De plus, de telles horloges doivent être placées dans des endroits stables afin de ne pas perturber le mouvement du pendule. Cette contrainte est incompatible avec la montre portée au poignet.
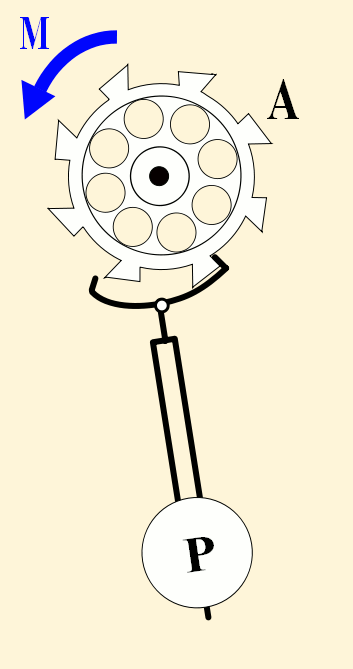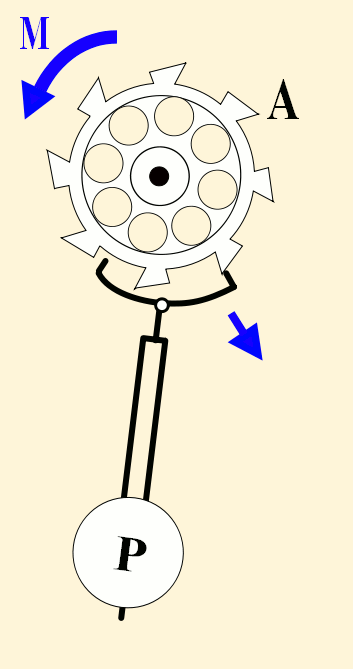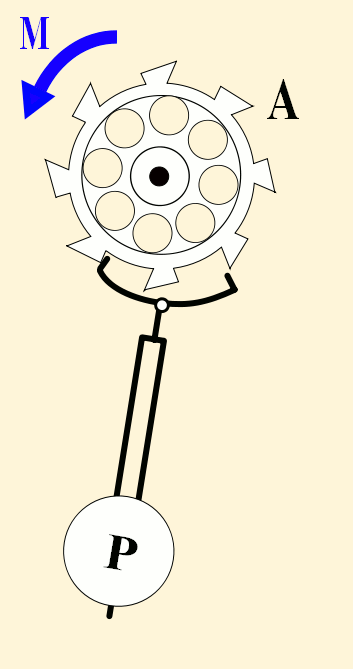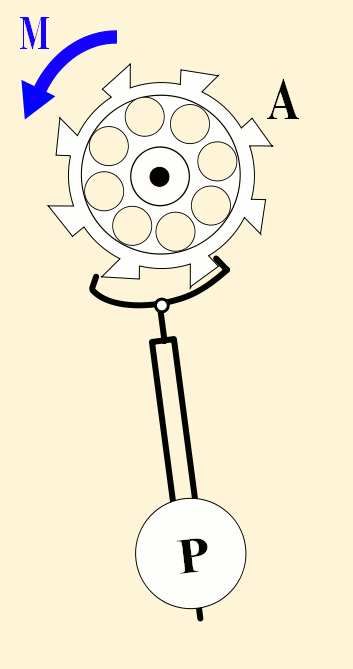
L'animation ci-dessous montre comment un mouvement d'horloge peut être régulé par un pendule et comment l'énergie est transmise à ce pendule.
On a réalisé au cours du temps un autre organe régulateur qui consiste en un volant d’inertie qui pivote autour d’un axe de rotation. Un ressort spiral (encore un) lui est accouplé et permet au volant d’inertie d’osciller autour d’un point d’équilibre.
Si l’on suppose qu’il n’y a pas de frottement, il suffit de donner une impulsion au volant d’inertie pour que celui-ci se mette à osciller. Il commence par tourner dans le sens de l’impulsion initiale, ce qui va comprimer (ou détendre) le ressort spiral. A partir d’un certain déplacement, la force du ressort spiral annulera l’impulsion initiale et fera tourner le volant d’inertie dans le sens opposé afin de le ramener à son point d’équilibre.
Arrivé au point d’équilibre, l’énergie cinétique accumulée par le volant d’inertie fait qu’il continuera son mouvement et dépassera ce point d’équilibre. Le ressort spiral va donc se détendre (ou se comprimer) ce qui aura pour conséquence de freiner le volant d’inertie, l’arrêter, et le ramener à son point d’équilibre. Et de nouveau, l’énergie cinétique acquise par le volant d’inertie fera qu’il dépassera ce point d’équilibre ce qui comprimera (ou détendra) le ressort spiral, et ainsi de suite.
La période d’oscillation autour du point d’équilibre est très stable dans le temps si l’ensemble est bien construit. On dispose donc de notre base de temps.
Il y a beaucoup de vocabulaire pour désigner ces oscillations et on peut vite s'y perdre. Les termes utilisés sont les suivants (lorsqu'il y a plusieurs désignations, elles sont séparées par des "/") :
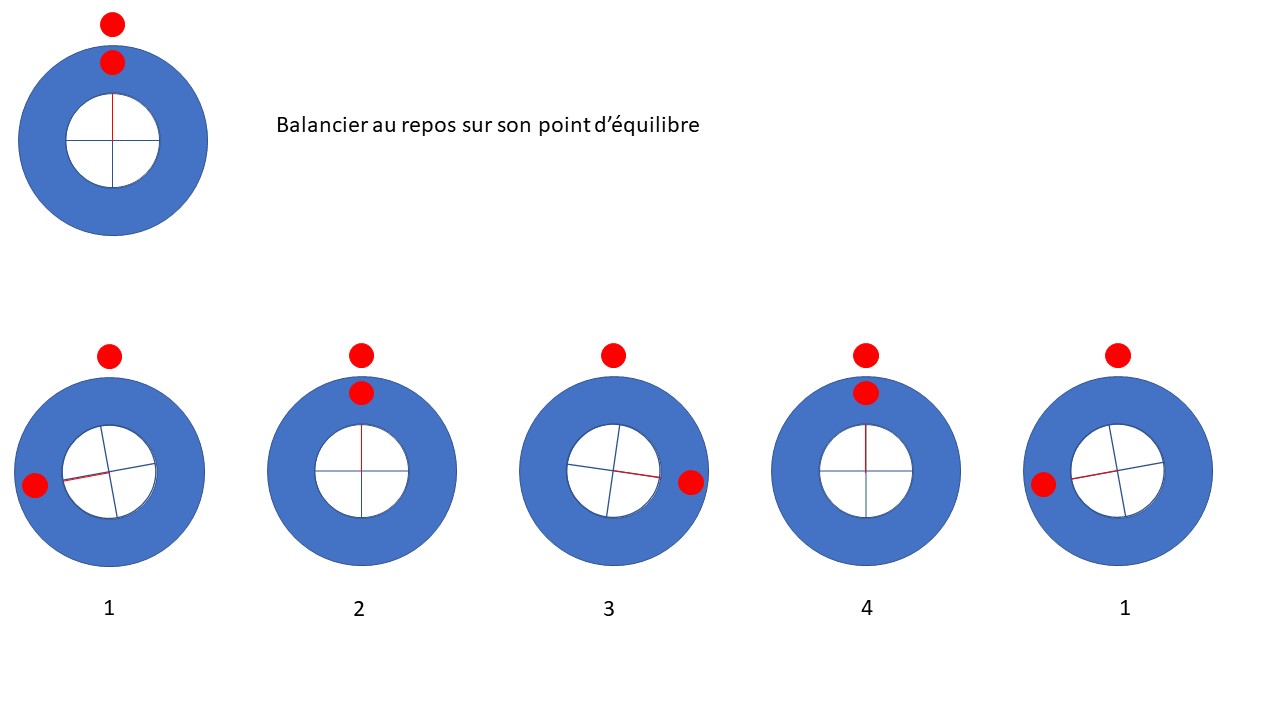
- Battements/ Alternances / oscillation / beat per hour : observez la figure au-dessous.
On y voit un balancier (c'est le nom de l'organe régulateur) au repos à son points d'équilibre marqué par le fait que les deux points rouge (celui sur le balancier et celui en dehors du balancier) sont face à face. C'est la position du balancier lorsqu'il ne bouge pas, parce que la montre n'est pas « remontée » par exemple. Cette position du balancier correspond à celle du ressort spiral lorsqu'il est complètement détendu. La vocation du ressort spiral, c'est de ramener le balancier à cette position qui est celle du point d'équilibre !
Faisons tourner le balancier vers la gauche (point rouge à gauche, position 1) puis lachons le. Le ressort spiral associé au balancier va le faire tourner vers la droite pour le ramener au point d'équilibre (position 2). Mais le balancier a une inertie et une fois qu'il sera passé devant ce point, il va continuer son mouvement vers la droite jusqu'à ce que le ressort spiral ait absorbé toute l'énergie du balancier (position 3).
Le ressort va donc tenter de ramener le balancier à sa position d'équilibre (position 4) mais pour les mêmes raisons que précédemment, une fois passé ce point, le balancier va continuer son mouvement vers la gauche jusqu'à ce qu'il se retrouve en position 1 (on suppose qu'il n'y a pas de frottements).
Cet aller et retour correspond à une séquence complète d'une oscillation du balancier ou un battement et on a constaté qu'il est passé deux fois devant son point d'équilibre. On verra par la suite que cet aller et retour génère deux chocs audibles, le fameux Tic Tac de la montre.
Le nombre de battement par heure est une caractéristique importante de la montre, qui dépend de sa fabrication et dans une certaine mesure, de sa précision. Des valeurs courantes vont de 18000 battements par heures jusqu'à 36000 battements par heures. - Fréquence / frequency : la fréquence se mesure en Hertz (nombre d'oscillations par seconde). La fréquence d'une montre est donc le nombre de battements par seconde. Fréquence de la montre = nombre de battements par heure / 3600.
- Période / period : par définition, la période est l'inverse de la fréquence et se mesure en seconde (c'est une durée). La période d'une montre vaut donc 1 / Fréquence de la montre.
- Demi-période : c'est évidemment la moitié de la période. Pourquoi s'intéresser à cette valeur ? Parce qu'elle permet de calculer simplement la durée minimale que peut compter une montre.
Supposons que le nombre de battements d'une montre vaille 18000 par heure. Sa fréquence est donc de 18000/3600 = 2,5Hz. Sa période vaut 1/2.5 = 400ms et sa demi-période vaut donc 200ms qui est donc la plus petite durée que va mesurer la montre. Généralement, on associe cette durée à l'aiguille des secondes. Cela veut dire que l'aiguille des secondes avancera de 200ms à chaque oscillation du balancier et il lui faudra avancer 5 fois pour mesurer une seconde.
Un chronomètre (start-stop) avec un tel battement pourra au mieux mesurer les temps au 1/5 de seconde.
Récapitulatif :
- Nombre de battements Bh par heure (nombre de « Tic » ou de « Tac ») par heure.
- Fréquence du battement Fs = Bh / 3600
- Période du battement en millisecondes (ms) avec P = 1/Fs (durée entre deux « Tic » ou entre 2 « Tac »)
- Durée D d’un « Tic » ou d’un « Tac » = P/2
Le tableau ci-dessous donne les valeurs des fréquences et périodes pour différents battements courants :
| Bh | Fs | P | D |
| 18000 | 2,5Hz | 400ms | 200ms |
| 21600 | 3,0Hz | 333ms | 166ms |
| 28800 | 4,0Hz | 250ms | 125ms |
| 36000 | 5,0Hz | 200ms | 100ms |
Maintenant que nous disposons de cette base de temps, il nous reste deux points à régler :
- Comment l’utiliser pour réguler le mouvement de la montre ?
- Comment lutter contre les frottements qui font perdre de l’énergie au balancier et qui finissent par l’arrêter à son point d’équilibre ?
Le secret pour le premier point réside dans le mécanisme dit « d’échappement ». Il en existe de plein de sortes et il n’est pas dans l’objet de cette introduction de les décrire tous. Je me contenterai de prendre l’exemple de l’échappement dit « à ancre suisse » (un des plus répandu) pour faire saisir le principe du dispositif.
On trouve plein de vidéo sur l’Internet montrant le fonctionnement de cet échappement. Je vous conseille de les regarder pour vous familiariser avec son mouvement.
Par contre, les explications sont parfois difficile à comprendre car en pratique, cet échappement réalise deux fonctions étroitement combinées et que ces deux fonctions sont le plus souvent décrites simultanément.
Pour ma part, je vais les expliquer l’une après l’autre ce qui me semble plus simple à appréhender.
Régulation d'une montre
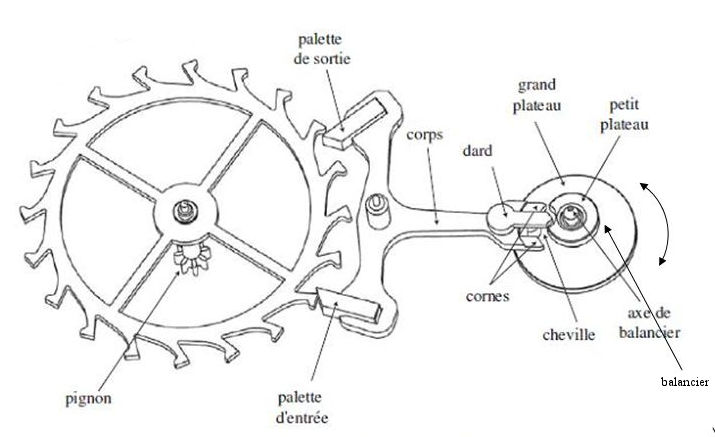
À gauche de l’illustration se trouve une roue ayant une forme un peu particulière que l’on appelle « roue d’échappement ». Il ne s’agit pas d’un engrenage au sens habituel du terme même s’il y a des dents, d’une forme un peu particulière cependant.
Notez également la présence de l’engrenage (pignon) associé à cette roue d’échappement.
Supposons que nous exercions une force sur ce pignon visant à faire tourner cette roue dans le sens horaire.
Considérez l’ancre avec ses palettes et son axe sans vous occuper de l’axe du balancier à droite.
Manipulons l’ancre de façon à ce que la palette dite « de sortie » se place profondément entre les dents de la roue d’échappement. Vous remarquerez alors que la palette dite « d’entrée » se trouve en dehors du chemin parcouru par ces mêmes dents.
La roue d’échappement elle-même est bloquée par la palette de sortie sur laquelle butte la dent qui se trouve à gauche de la palette de sortie.
Cette manipulation peut se faire en poussant le corps de l’ancre vers la gauche sur le schéma.
Poussons maintenant le corps de l’ancre vers la droite.
La palette de sortie va se dégager, laissant libre la dent qu’elle bloquait à sa gauche. Dans le même temps, la palette d’entrée va se placer dans l’espace libre entre deux dents de la roue d’échappement mais pas n’importe où dans cet espace libre : assez loin de la dent qui se trouve à sa gauche.
Du coup, la roue d’échappement qui cherche à tourner dans le sens horaire va pouvoir réaliser sa vocation : tourner. Mais pas longtemps. Car très vite, la dent qui se trouve à gauche de la palette d’entrée va se trouver bloquée par cette palette.
Poussons maintenant de nouveau le corps de l’ancre vers la gauche.
La dent qui se trouve bloquée par la palette d’entrée va se dégager. Pendant ce temps, la palette d’entrée va se placer dans l’espace libre entre deux dents de la roue d’échappement, mais pas n’importe où dans cet espace libre : assez loin de la dent qui se trouve à sa gauche.
Du coup, la roue d’échappement qui cherche à tourner dans le sens horaire va de nouveau pouvoir réaliser sa vocation : tourner. Mais pas longtemps. Car très vite, la roue qui se trouve à gauche de la palette de sortie va se trouver bloquée par cette palette.
Si vous êtes obstiné et patient, vous pouvez pousser alternativement et régulièrement à droite et à gauche le corps de l’ancre. L’ancre se déplacera d’un cran à chaque fois que vous changerez de sens et pas plus, pas moins, et selon le rythme que vous imposerez au mouvement de l’ancre.
Imaginons maintenant que ce ne soit pas vous qui manipuliez l’ancre mais la balance.
Observez la forme particulière de l’ancre à sa gauche et oubliez le dard. Il reste les deux cornes.
Observez maintenant le grand plateau. Ce plateau est solidaire de la balance. Une petite cheville est prévue pour se placer entre les deux cornes.
Lorsque la cheville va vers la droite, elle pousse le corps de l’ancre vers la droite puis elle continue son chemin.
Puisque le corps de l’ancre est allé sur la droite, la palette d’entrée s’est dégagée de la roue d’échappement tandis que la palette de sortie se place entre deux dents de la roue d’échappement.
Au bout d’un certain temps, la balance va inverser son sens de rotation. La cheville va revenir en allant vers la gauche. Elle va entrer dans les cornes de l’ancre et pousser l’ancre vers la gauche.
Puisque le corps de l’ancre est allé sur la gauche, la palette de sortie s’est dégagée de la roue d’échappement tandis que la palette d’entrée se place entre deux dents de la roue d’échappement.
Et à chaque fois que se produit cette inversion de sens, la roue d’échappement avance d’un cran, au rythme imposé par le balancier. Et comme notre balancier est l’organe régulateur, nous avons le moyen de réguler le reste de la montre : il suffit que le pignon de la roue d’échappement soit en liaison avec le train d’engrenage que nous avons décrit précédemment.
En général, le barillet fournit son énergie à l’engrenage des secondes et l’engrenage des secondes est relié à la fois au train d’engrenage qui actionne les aiguilles et à la roue d’échappement.
Entretien de la base de temps
Comme précédemment, nous avons négligé les frottements, en particulier, ceux qui s’appliquent au régulateur, c’est-à-dire, au balancier. Mais évidemment, ces frottements existent et il faut trouver le moyen d’entretenir le mouvement d’oscillation du balancier.
C’est là qu’intervient la deuxième fonction de l’ancre suisse : redonner de l’énergie au balancier.
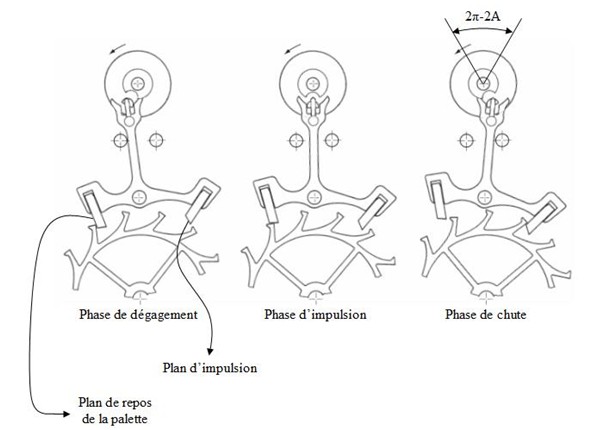
Cette énergie est transmise lors du dégagement des palettes. La forme particulière de la dent vient frotter contre la palette, sur son « plan d’impulsion », ce qui permet de transmettre l’énergie au balancier via la cheville.
Cette énergie fournie doit être supérieure (ou au pire égale) à l’énergie perdue à cause des frottements. En pratique, elle ne sera jamais suffisante pour faire « trop » tourner le balancier dont la période de rotation est par ailleurs fixe. C’est le ressort spiral qui se chargera d’absorber le surplus d’énergie éventuel.
Limitation des frottements
Et voilà, vous savez concevoir une montre. Comme dit précédemment, la construire est une autre affaire !
Tout d’abord, on a pu voir que les frottements étaient l’ennemi de la marche des trains d’engrenage ; l’énergie se perd dans ces frottements ce qui tend à arrêter le mécanisme.
Pour les limiter, les axes des engrenages doivent être très fins afin de diminuer leur surface de frottement avec ce qui les maintient dans la montre. Les axes sont maintenus par le corps de la montre qui est en général en métal, comme les axes eux-mêmes.
Métal sur métal, ce n’est pas très bon. Les frottements induits créent également une usure (du corps de la montre et des axes) ce qui amène à la détérioration définitive de la montre au bout d’un certain temps.
Pour limiter ce phénomène, les axes qui tournent le plus vite passent par des « coussinets » qui sont en « rubis » (jewels en anglais pour joyaux) afin de limiter les frottements et l’usure. Une lubrification adéquate permet encore de limiter ces frottements et donc l’usure. À noter que ce que l’on appelle rubis est en fait depuis le début du XXème siècle un matériau synthétique qui n’est pas du rubis mais aujourd’hui du corindon.
Certaines montres sont marqués 15, 18, 21, 32 rubis/jewels. On a souvent considéré que plus il y avait de rubis, meilleure était la qualité de la montre ce qui n’est pas faux mais n’est pas complètement vrai non plus.
Pourquoi autant de rubis ?
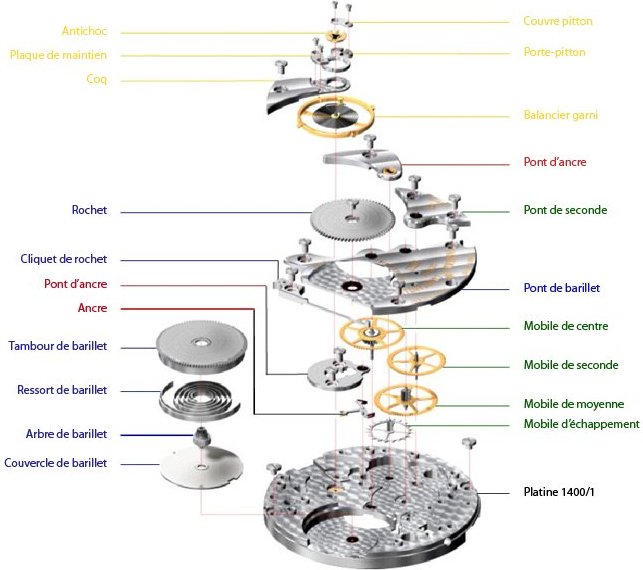
Le balancier tourne très vite et est un élément particulièrement fragile. Généralement, l’axe du balancier passe par deux rubis (pivots) et les extrémités de l’axe repose sur deux autres rubis (contre pivots) montés sur des suspensions. Le rôle de ces suspensions est d’absorber les chocs afin d’éviter la casse de l’axe du balancier. Ça fait 4 rubis.
L’échappement ainsi que la roue d’échappement sont également des pièces qui bougent beaucoup. Les axes sont donc également maintenus par des rubis. Cela fait 4 rubis de plus. Pour les montres plus recherchées, la roue d’échappement peut également être montée sur des contre pivots ce qui rajoute 2 rubis de plus. On n’en tiendra pas compte ici.
Dans les ancres suisses, les palettes sont en rubis ainsi que la cheville qui actionne l’échappement. Cela fait 3 rubis supplémentaires. A ce stade, on a donc 11 rubis. Ceux-ci sont les plus critiques.
En général, certains axes des trains d’engrenage (ceux qui tournent le plus vite) sont montés sur rubis. On peut donc avoir 4 à 6 rubis supplémentaires. Disons 4 ce qui nous fait 15 rubis, le standard pour les montres simples avec heures, minutes et secondes.
Et voici une photo d'un mouvement chinois Seagull.

FEMGA 45
Vous pouvez voir le détail d'un mouvement simple en suivant ce lien (FEMGA 45, mouvement pour montre de femme) avec les différentes versions, la façon de le démonter et de le remonter.
REMONTAGE AUTOMATIQUE
Exposé du problème
Comme nous l’avons vu précédemment, l‘énergie de la montre est contenue dans un ressort à l’intérieur du barillet. Périodiquement, il faut retendre ce ressort afin qu’il emmagasine l’énergie destinée à animer la montre.
Dans les montres à remontage manuel, un bouton, nommé « couronne » qui permet, via une tige de remontoir et d’un pignon de faire tourner l’arbre du barillet via un engrenage que l’on appelle le « rochet ». Cette action permet d’enrouler le ressort du barillet sur lui-même autour de l’arbre du barillet. Un cliquet permet d’éviter que l’arbre du barillet puisse tourner dans l’autre sens que celui du remontage.
Récupération d’énergie
L’invention d’un système de remontage automatique de la montre remonte à la fin du 18è siècle. Tout le monde n’est pas d’accord sur qui est l’inventeur. Ce que nous pouvons dire ici, c’est que le moment était venu que ce dispositif soit inventé, et sans doute, par plus d’une personne.
L’idée du remontage automatique consiste à utiliser le mouvement naturel du bras du porteur de la montre pour transmettre de l’énergie au barillet de la montre. Si l’on s’y prend bien, la montre est remontée en permanence tant que la personne est active. Lorsque la montre n’est pas portée ou que la personne est inactive, la « réserve de marche » de la montre permet de continuer à faire fonctionner la montre jusqu’à ce que son porteur soit de nouveau actif.
Une réserve de marche courante est de l’ordre de 35 à 40 heures. Elle correspond à la compression maximum du ressort dans le barillet. En pratique, cette réserve est moins importante.
A ce stade, il faut trouver un moyen de transmettre l’énergie incontrôlée produite par le mouvement naturel du bras au ressort du barillet.
Pour récupérer et canaliser cette énergie, le moyen le plus courant consiste à utiliser un rotor fixé au centre de la montre (sur sa face arrière) et dont l’extrémité comporte une masse.
Lorsque l’on bouge la montre, le rotor tourne autour de son axe, dans un sens ou dans un autre. Ce mouvement de rotation est ensuite transmis par une série d’engrenages (dont le premier est solidaire du rotor) au rochet associé à l’arbre du barillet ce qui « remonte » la montre.
La photo ci-dessous est celle d’une montre Oméga sur laquelle on distingue le rotor avec sa masse.

Parfois, le rotor n’est pas fixé au centre de la montre mais dans à autre endroit. C’est le cas de la montre Universal Polerouter présentée ci-après et de son Microtor. Le rotor est beaucoup plus petit que dans le cas précédent. Il peut être logé dans l’épaisseur du mécanisme ce qui permet de faire des montres plus plates. Je ne sais pas pourquoi cette approche ne s’est pas généralisée.

L’énergie que le rotor récupère est celle de l’accélération. Cette accélération provient du mouvement de votre bras et/ou de la force de gravité terrestre.
Comme elle est faible, il faudra augmenter le couple par un système d’engrenage qui réalisera une réduction (voir les chapitres précédents).
Transmission de l’énergie
Dans la présentation précédente, on a fait l’hypothèse que le rotor pouvait tourner dans un sens ou dans un autre. Le problème est que le remontage ne peut se faire que dans un sens : celui qui permet d’enrouler le ressort du barillet autour de l’arbre du barillet.
Lorsque le rotor tourne « dans le bon sens », il n’y a pas de problème. Le bon sens est défini ici comme étant celui qui fait tourner le dernier engrenage du train d’engrenage entre le rotor et le rochet dans le sens inverse du remontage.
On a un problème lorsque le rotor tourne dans le « mauvais sens ». Plusieurs techniques ou stratégies ont été mises en œuvre pour régler ce problème.
La première stratégie consiste à empêcher le rotor de tourner dans le mauvais sens. Cette approche permet de réaliser un système de remontage à moindre coût et il est efficace. Le mouvement 8205 de la société Miyota utilise cette approche.
La seconde stratégie consiste à mettre en place un inverseur de sens. Plusieurs techniques ont été imaginées pour ce faire et certaines sont relativement complexes d’un point de vue mécanique.
Le site horlogerie Suisse expose le principe d’un de ces inverseurs. Comme cette explication est très bien faite, je ne vais pas la détailler ici. Je n’en rappellerai que les principes au cas où la page viendrait à disparaitre.
L’engrenage sous le rotor est en contact avec deux engrenages particuliers que l’on appelle « roues à cliquet montées ». Une roue à cliquet montée comporte deux engrenages montés l’un sur l’autre. L’engrenage en contact avec celui du rotor que l’on appellera « engrenage supérieur » est plus petit que l’engrenage. L’engrenage inférieur est quant à lui en contact avec la deuxième roue à cliquet.
L’astuce est qu’entre l’engrenage inférieur et l’engrenage supérieur se trouve des cliquets qui sont montés de telle sorte que lorsque la roue supérieure tourne dans un sens, le cliquet entrainera la roue inférieure via un trou percé dans cette roue et que lorsque la roue supérieure tourne dans l’autre sens, le cliquet se dégagera du trou de la roue inférieure et glissera sur cette roue.
Une des roues supérieure entraine sa roue inférieure lorsque le rotor tourne dans un sens donné, l’autre roue supérieure entraine sa roue inférieure lorsque le rotor tourne dans l’autre sens.

Roue à cliquet
Une première roue est connectée au rochet via un train d’engrenage. C’est celle qui, pour le « bon sens » de rotation du rotor fait tourner le rochet également dans le bon sens. Lorsque le rotor tourne dans le bon sens, les cliquets permettent l’entrainement de la roue inférieure par la roue supérieure. Lorsque le rotor tourne dans le mauvais sens, la roue supérieure se désolidarise de la roue inférieure car les cliquets se désengagent.
Le même raisonnement s’applique pour la deuxième roue à cliquet pour le sens inverse de rotation du rotor (le « mauvais sens »). La seule différence est que cette deuxième roue n’est pas reliée au train d’engrenage qui va au rochet mais à la roue inférieure de la première roue à cliquet ce qui permet de réaliser une inversion de sens.
Il n’y a pas de risque de blocage du système car pour chaque sens de rotation du rotor, une des deux roues inférieure de la roue à cliquet sera toujours libre.
La réalisation mécanique est assez complexe ce qui entraîne un coût du système largement plus élevé que lorsque l’on ne gère qu’un seul sens de rotation.
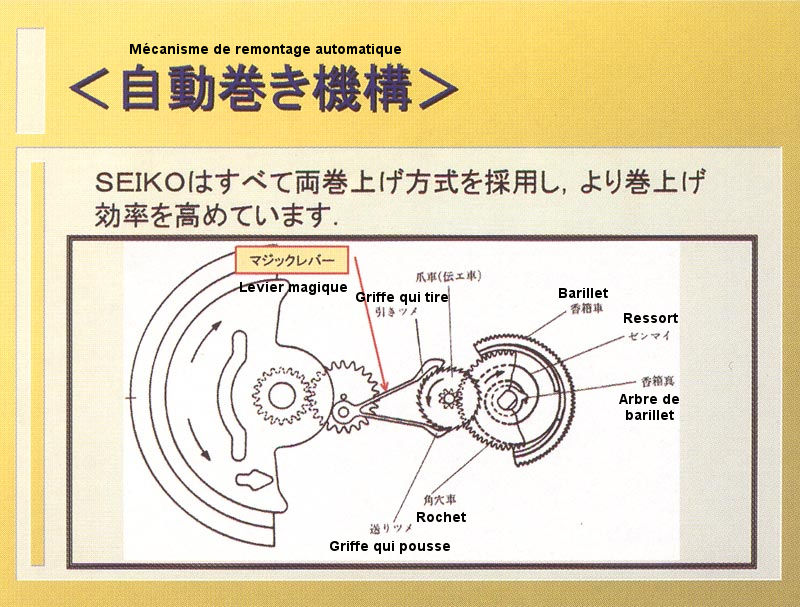
La firme Seiko a imaginé un autre mécanisme de transmission qui accepte les deux sens de rotation du rotor et qui est d’une grande simplicité et d’un faible coût. Certains considèrent que c’est une des raisons du succès de la marque. Je l’appellerai « pousse-tire » par la suite (son vrai nom est magic lever).
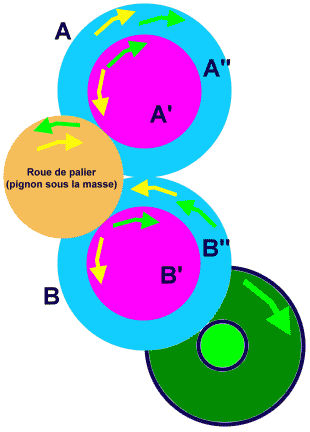
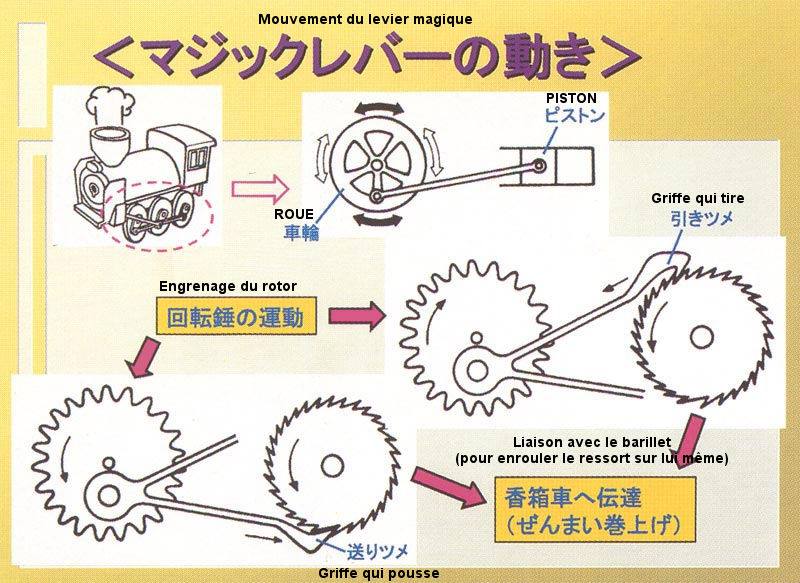
Imaginez une roue crantée autour de laquelle se trouvent deux petites griffes. L’une des griffes agrippe la roue crantée pour la faire tourner dans un sens, l’autre griffe fait de même pour la faire tourner dans l’autre sens. En d’autres termes, l’une des griffes pousse les crans dans un sens, l’autre griffe tire les crans dans l’autre sens. Pour expliquer ce mécanisme, Seiko fait une analogie avec le fonctionnement de la transmission d'une locomotive à vapeur.
Les leviers qui tiennent ces griffes sont reliés entre eux sur une rondelle. Cette rondelle est positionnée sur un axe se trouvant sur un engrenage. Mais cet axe est excentré par rapport à l’axe de l’engrenage.
Ainsi, lorsque l’engrenage tourne, les leviers vont réaliser un mouvement de va et vient. Par exemple, un des leviers montera lorsque l’autre descendra. Puis, au fur et à mesure que l’axe excentré tourne, le levier qui montait descendra alors que le levier qui descendait montera. Et ceci est vrai quel que soit le sens de rotation de l’engrenage qui porte l’axe excentré.
Lorsque le levier qui porte la griffe qui tire monte, la forme de la griffe fait qu’elle glissera sur la roue crantée. Par contre, l’autre griffe qui pousse agrippera cette roue et la fera tourner dans un sens, toujours le même.
Et inversement, lorsque le levier qui porte la griffe qui tire descend, la forme de la griffe fait qu’elle agrippera la roue crantée. Par contre, l’autre griffe qui pousse glissera sur cette roue.
Il n’y a pas besoin de pièces de grande précision ni de grande complexité pour réaliser ce mécanisme. Le seul défaut éventuel est qu’avec le temps, les griffes ou la roue crantée pourront finir pas s’user. Pour ma part, je n’ai pas vu beaucoup de cas d’usure, sauf sur des montres dont la roue crantée était grippée.
Une petite animation pour mieux comprendre :

En cliquant sur l'image, vous pouvez voir une animation en 3D du Magic Lever par C. Yamahata sur sketchfab.com
REGLAGE D'UNE MONTRE
Il existe une foule de sites et de documents très bien faits pour expliquer comment fonctionnent les montres, en particulier, les montres à échappement à ancre suisse. J'en donne quelques uns dans le corps du documents. Je n'ai donc mis ici que le strict minimum pour comprendre le fonctionnement et l'usage des chronocomparateurs.
Préambule
Le chronocomparateur est un appareil qui est utilisé pour mesurer la régularité du mouvement d’une montre et son exactitude par rapport à ses spécifications. Le but est de permettre le réglage de la montre afin de minimiser son avance ou son retard et éventuellement, l’égalité de la durée entre le Tic et le Tac et ce, quel que soit la position de la montre (horizontale, penchée, verticale, retournée…).
Pour comprendre comment fonctionne un chronocomparateur, il est utile de faire quelques rappels sur les échappements.
Bruits de battements
Tout d'abord, un peu de lecture sur quelques sites parmi d'autres :
- horlogerie-suisse
- Un document de Witschi très complet.
Un Tic ou un Tac génère un « bruit de battement » qui se fait en trois étapes :
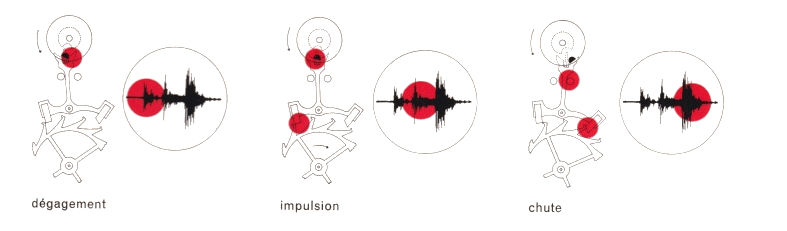
Tiré du manuel utilisateur du Vibrograf B200
- Le dégagement : la cheville de plateau (ou ellipse) heurte l’entrée de la fourchette. On nommera T1 le temps auquel se produit le dégagement.
- L’impulsion : une dent de la roue d’échappement sur le plan d’impulsion entre en contact avec une levée. On nommera T2 le temps auquel se produit l’impulsion.
- La chute : chute de la dent de la roue d’échappement sur l’autre levée. On nommera T3 le temps auquel se produit la chute.
Chacune de ces étapes crée un choc qui est détecté par le capteur.
Il est conseillé d’utiliser le choc généré par le dégagement comme point de départ de la mesure.
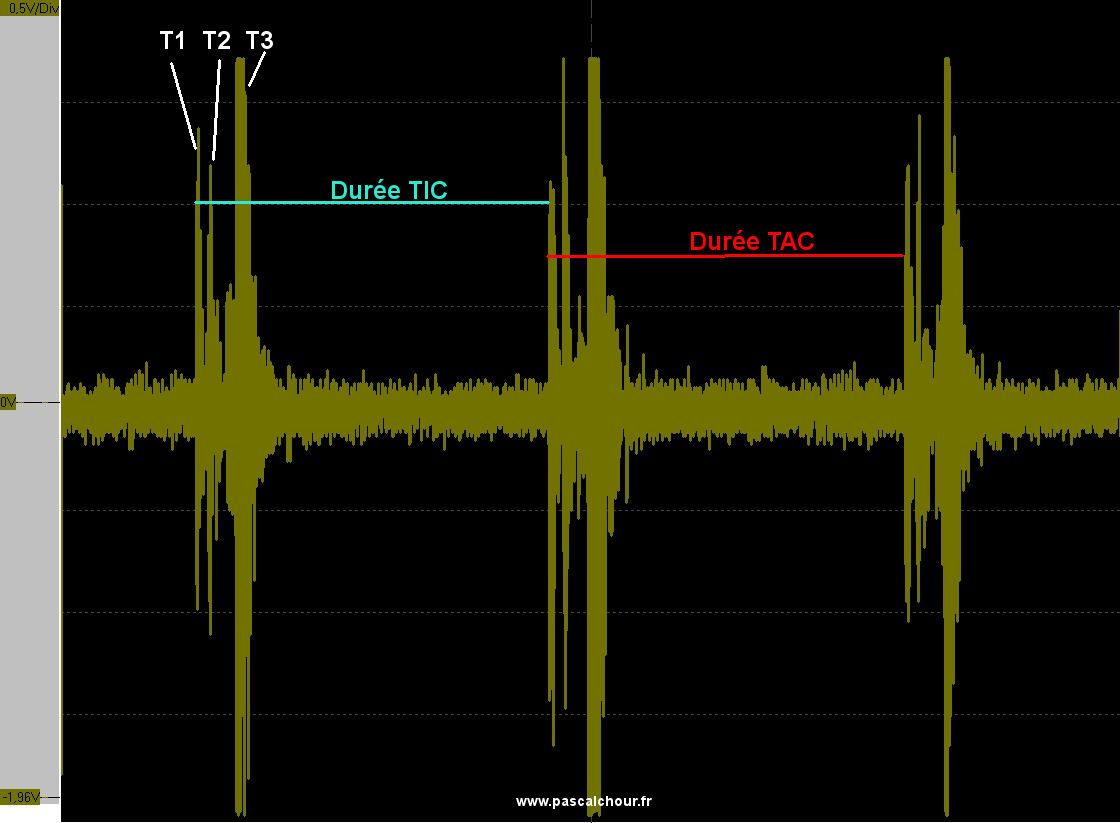
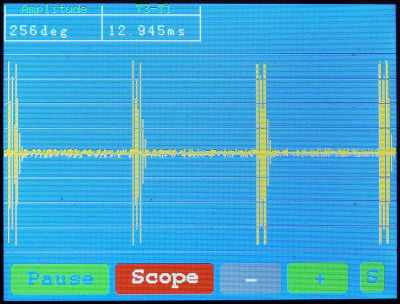
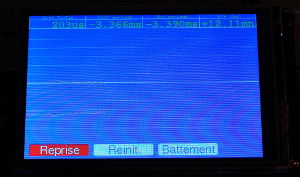
Exemple d'oscillogramme avec PC-RMx
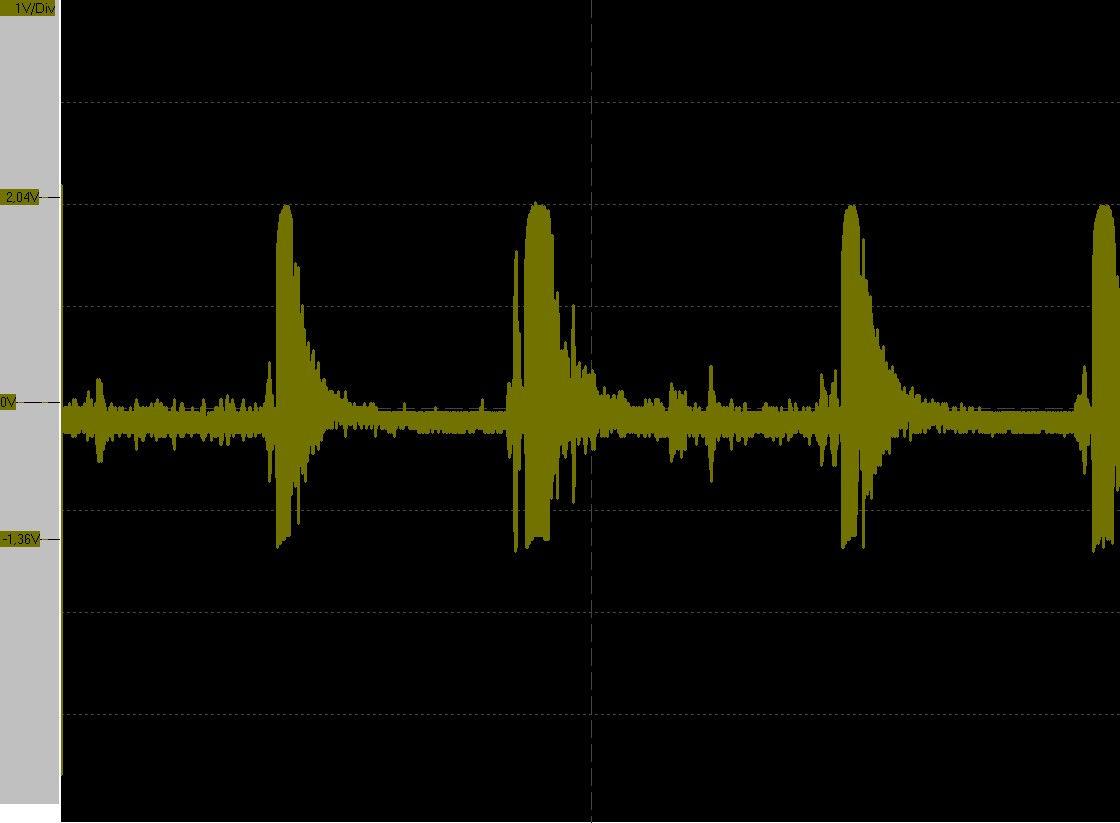
Bruits parasites
Sur une montre en mauvais état, il peut se produire d’autres chocs parasites. Un cas typique est celui du dard qui touche le plateau et qui produit un choc entre un Tic et un Tac. Il va de soi que dans ce cas, la mesure du chronocomparateur risque d’être perturbée et que l’on ne peut rien attendre de fiable de la mesure. D’ailleurs, pour faire simple, on ne peut régler une montre que si elle est en bon état. Mais le fait même que le chronocomparateur puisse être perturbé lors de son fonctionnement peut permettre dans certains cas d’identifier un défaut de la montre qui devra être réparé avant que l’on puisse entreprendre son réglage.
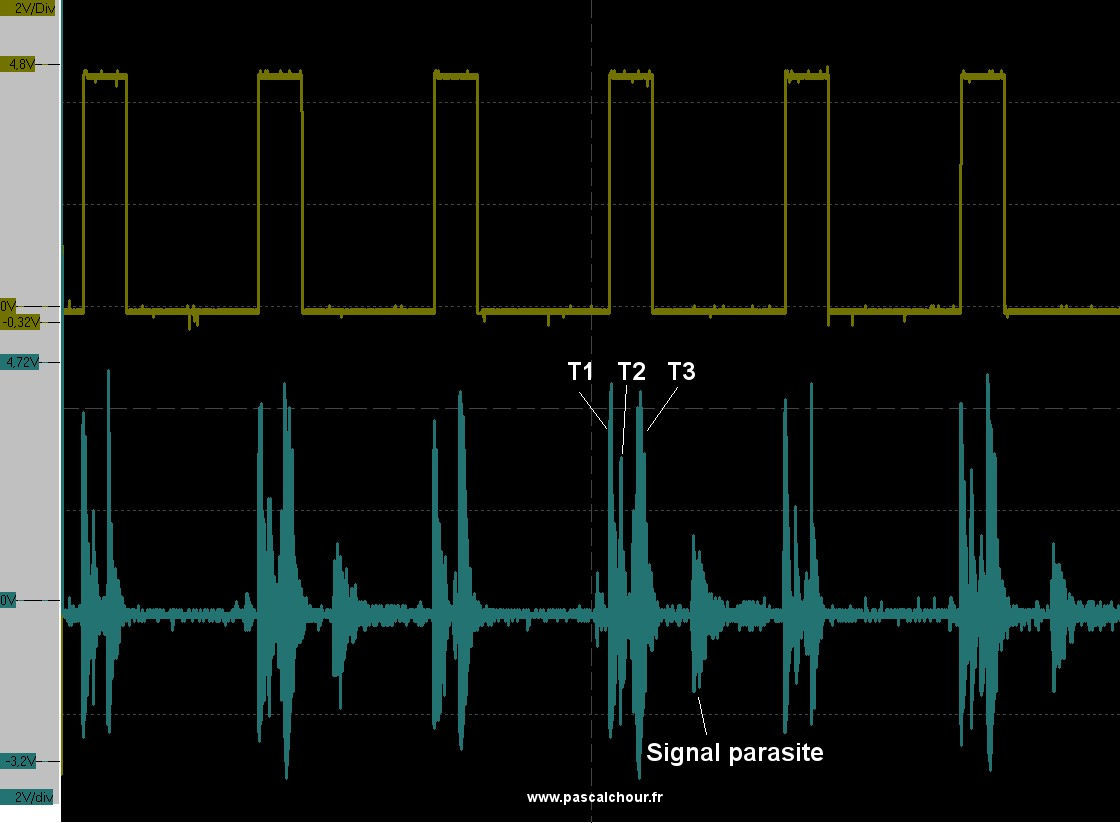
Signal bleu : signal de la montre avec signal parasite
Signal jaune : signal généré pour le chronocomparateur (PC-RM1)
Amplitude
Certains chronocomparateurs peuvent également mesurer en degrés l’amplitude du mouvement du balancier. Une amplitude insuffisante peut être le signe que la montre a besoin d’être lubrifiée. Les amplitudes courantes vont de 270° à 310°. Pour réaliser cette mesure, il est nécessaire de pouvoir mesurer le temps entre T1 et T3 et de connaitre l’ « angle de levée » du mouvement. Cet angle doit être entré en paramètre en degrés pour le calcul.
T = T3-T1 correspond au temps qu’il a fallu pour parcourir l’angle de levée (51° est une valeur usuelle). De manière générale, plus T3-T1 est grand, moins l’amplitude est importante. Si « n » est le nombre de battements par heure (18000, 21600…), alors la relation est la suivante tavec T en secondes) :
Amplitude = (3600 * AngleDeLevée)/(T*Pi*n)
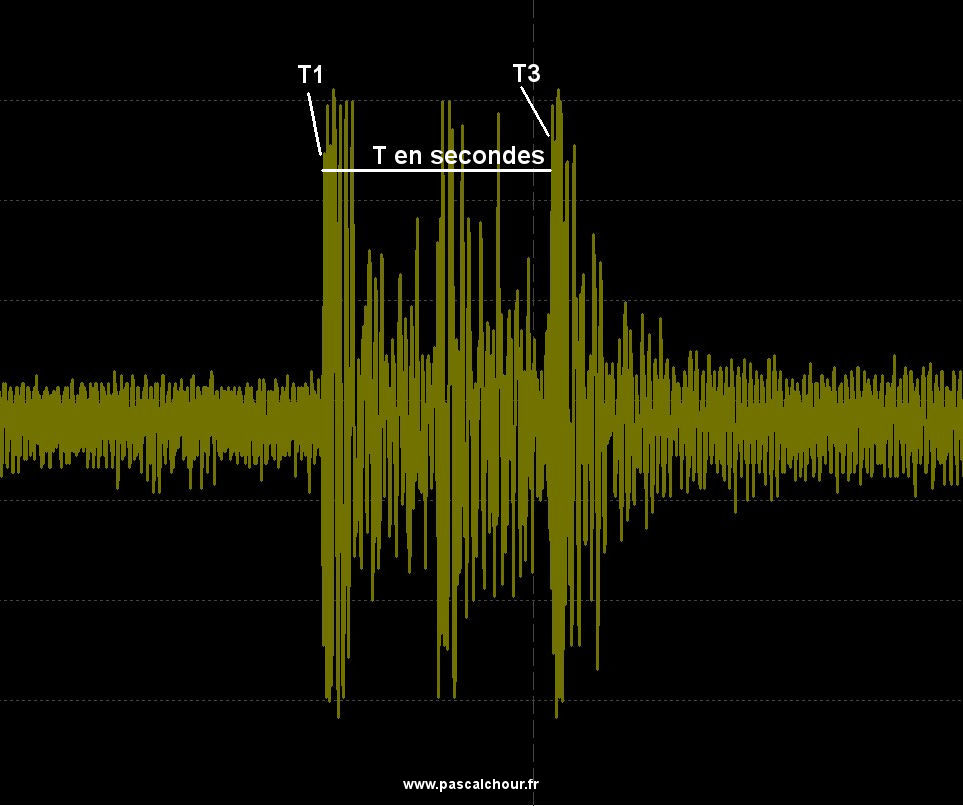
Mesure de l'amplitude. Dans cet oscillogramme, le signal est saturé
ce qui explique que tous les chocs sont au même niveau de tension.
Réglages
Les principales données de mesure étant définies, et la montre étant supposée en bon état (nettoyée, lubrifiée, pas de défauts), son réglage est assez simple. Les chronocomparateurs modernes affichent directement les valeurs en plus ou en moins par rapport aux valeurs attendues. Il y en a pour l'essentiel deux :
- Durée de la période (durée du Tic et du Tac) : pour une montre qui bat à 18000 coups par heure, la durée d'une période est de 400ms. En général, le
chronocomparateur affiche le nombre de millisecondes signé en plus ou en moins de la durée de la période attendue. Par exemple, -2ms signifie que la période mesurée est
inférieure de 2ms par rapport à celle attendue (dans l'exemple donné ici, la période mesurée est donc de 398ms).
Il faut alors agir sur la raquette d'avance retard pour minimiser cet écart.
Pour mémoire, une différence de 1ms (en valeur absolue) sur la période donnera un écart journalier (toujours pour une montre qui bat 18000 coups par heure) de :1x10-3x18000x24 = 432 secondes par jour soit 7mn.
Avant de faire le réglage, on aura intérêt à laisser le chronocomparateur acquérir suffisament de valeurs afin de travailler sur une moyenne de durée de périodes significative. Ce réglage doit être fait pour toutes les positions de la montre. Il faut parfois arriver à un compromis.
- Différence de durée entre un Tic et un Tac : une différence significative (plusieurs ms) de durée entre un Tic et un Tac signifie que le
balancier au repos n'est pas parfaitement en ligne avec l'ancre et l'axe de la roue d'ancre pour une ancre suisse.
Lorsqu'il est présent, le réglage se fera en agissant sur le porte-piton mobile. S'il est fixe, c'est plus compliqué...
Montre à quartz
A priori, il n'y a rien à régler dans une montre à quartz. Toutefois, on peut vouloir vérifier sa marche. Un chronocomparateur peut également mesurer la précision de la montre en captant le battement du passage des secondes. Un exemple ci-dessous sur une montre chonomètre Seiko avec un mouvement 7T32.
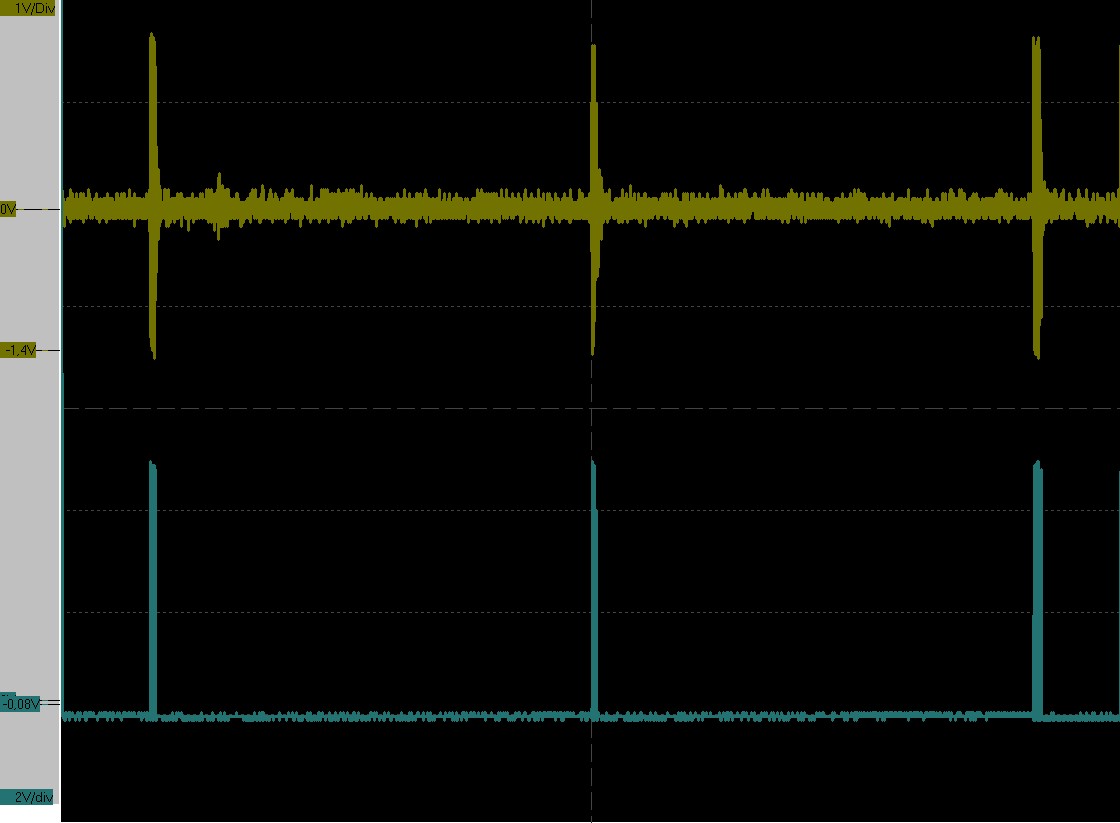
Chaque division en abscisse correspond à 200ms et il y a 5 divisions entre deux impulsions.
Même mesure mais avec le chronomètre en marche.
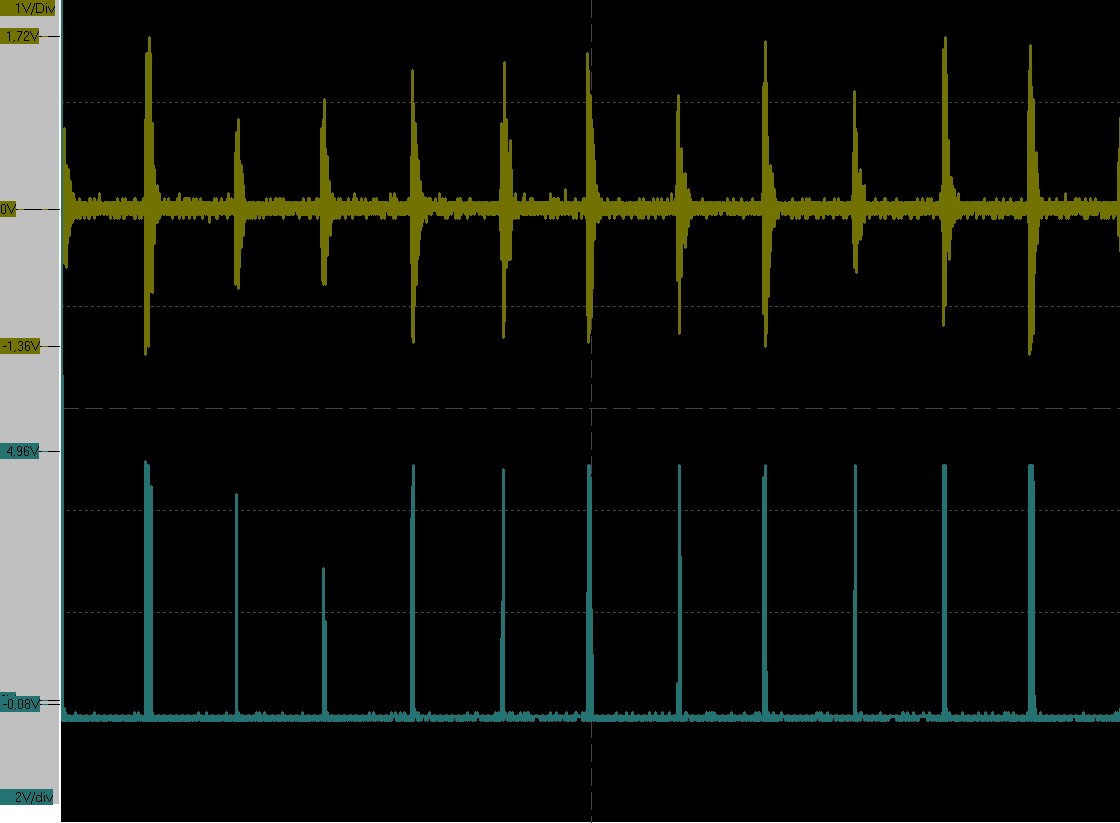
Il y a une division de 200ms entre chaque impulsion. Le chonomètre mesure effectivement au cinquième de seconde.
REGLAGE PENDULES (mouvement de Paris et autres)

Le réglage d'une pendule à balancier avec un chronocomparateur type PC-RM4 peut se faire d'une façon similaire à celui d'une montre, moyennant l'utilisation d'un capteur adapté. Encore faut-il connaitre la période d’oscillation de la pendule. Et puisqu’on parle de chronocomparateur, on parlera plutôt de son nombre de battements (le nombre de TIC et de TAC) par heure qui vaut en général deux fois le nombre d’oscillations par heure.
Et si on ne dispose pas d'un chronocomparateur comme PC-RM4, on pourra se rabattre sur PC-RM5 qui est plus simple à construire, très peu coûteux et dédié aux horloges.
Plusieurs sites très bien fait abordent ce point. En voici deux qui m’ont été utiles :
- Le Garde-Temps de Jean Claude Sulka, maître horloger.
- Le mouvement de Paris.
Quelques constantes
Pour les calculs qui suivent, on a besoin de connaitre quelques constantes :
- g est l’accélération de la pesanteur (typiquement, 9,802 ms-2).
- Pi = le nombre π (environ 3,1416)
- Pouce français : 27,048mm
- Ligne française : 2,254
La méthode la plus sûre
On calcule le facteur de démultiplication entre la la roue d’échappement et la roue de centre afin de connaitre le nombre d’alternances (liées au nombre de dents de la roue d’échappement) qui sont nécessaires pour que la roue de centre fasse un tour complet. Cette méthode donne directement le nombre de battements par heures. Voir par exemple https://sulka.fr/bal/ pour plus de précisions (et sinon, la présente page pour calculer les facteurs de démultiplication/multiplication).
L’ennui est qu’il faut compter le nombre de dents des roues et des pignons ce qui est fastidieux et impose en général le démontage du mécanisme.
Note : pour le comptage des dents des roues, j’applique la roue sur un papier, je passe un crayon autour de la roue puis je compte les dents en les marquant sur le papier.
Connaissant le nombre de battements par heure, on peut calculer la longueur du balancier en mm :
Lg = (3600 / (BatHeure x 2 x Pi))² x g x 1000
Une fois que l’on dispose du nombre de battements, le réglage avec un chronocomparateur du type de PC-RM4 est immédiat.
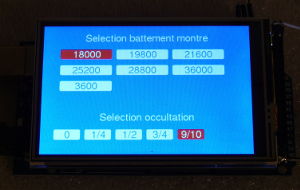
- On entre le nombre de battements.
- On positionne au mieux la lentille en fonction de la longueur calculée du balancier.
- On effectue la mesure du battement réel.
- Le chronocomparateur indique l’écart du battement réel par rapport au battement attendu (en plus ou en moins).
- On descend la lentille (l’horloge avance) ou on monte la lentille (l’horloge retarde) de façon à minimiser cet écart et on revient en 3 jusqu’à ce qu’on ait obtenu un écart le plus faible possible.
Une méthode approximative
Certaines pendules à mouvement de Paris comportent une inscription en pouces et lignes de la longueur du balancier (entre le point d’accroche et le centre de la lentille) ce qui peut donner une idée de sa période d’oscillation. Malheureusement, plusieurs éléments font que cette longueur n’est qu’une approximation et dépend de plusieurs paramètres qui ne peuvent être pris en compte. Mais on a déjà une approximation. Le calcul se fait de la façon suivante :
Si P est le nombre de pouces et L le nombre de lignes, la longueur Lg du balancier en millimètre vaut :
Lg = P x 27,048 + L x 2,254
Exemple : pour P=6 et L=8, on aura une longueur de balancier d’environ 180mm
Le nombre de battements approximatif par heure vaut :
BatHeureApprox = (3600) / (2 x Pi x (lg/(1000*g))-2)
Exemple : pour Lg = 180mm, on aura un nombre de battements par heure d’environ 4229.
On paramètre alors le chronocomparateur avec cette valeur, on règle la lentille à la longueur indiquée et on peut mesurer l’écart de l’horloge par rapport à ce qui est attendu. Sauf que comme le calcul du battement n’est qu’une approximation (d'où son nom : BatHeureApprox), cet écart sera faux. Alors comment faire ?
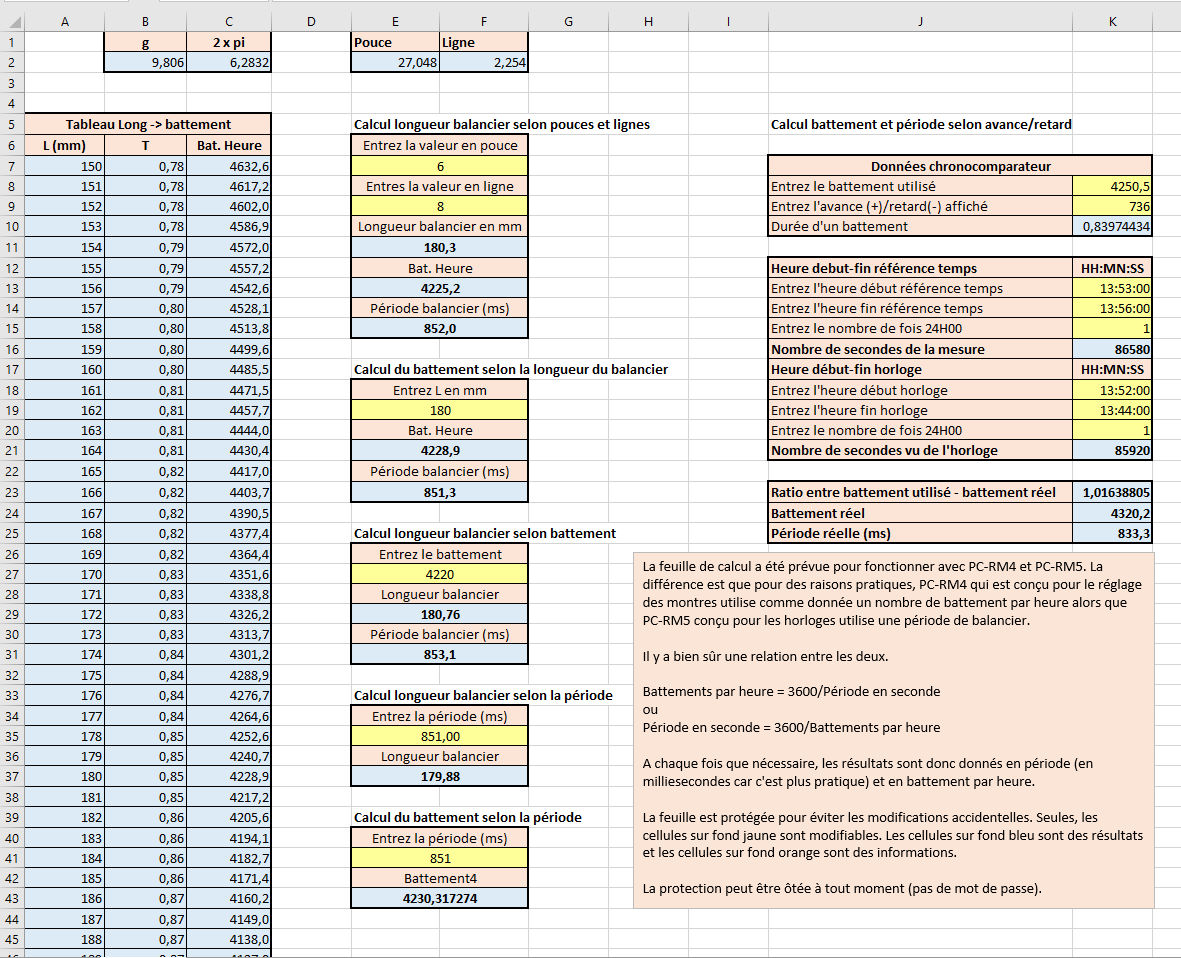
Dans ce qui suit, on a à la fois les équations et un exemple réel. A noter que BatHeureApprox vaut 4250,5 dans cet exemple.
On note l'heure de la pendule à régler en fonctionnement et l'heure d'une référence de temps (une montre à quartz par exemple). On suppose pour l'exemple que l'horloge indique 13H52 et la montre 13H53.
Au bout d'un certain temps (disons plus que 12H00, idéalement, 24H00), on note l'avance ou le retard entre la pendule et la montre ainsi que l'heure de la montre. On suppose pour l'exemple que la pendule indique 13H44 et la montre 13H56. Cela veut dire qu'en 24H03mn (soit 86580 secondes que l'on note Dureemesure), la pendule a réellement retardé de 12mn soit ARRéel=-660 secondes (signe moins car il s'agit d'un retard).
On calcule le nombre de secondes écoulées sur la durée de la mesure mais du point de vue de l'horloge que l'on note Dureehorloge. Il s'agit de la différence entre l'heure relevée à la fin de la mesure (13H44 dans l'exemple) et l'heure du début de la mesure (13H52 dans l'exemple).Donc, Dureehorloge = 85920 secondes dans l'exemple choisi.
On note l’avance (+) ou le retard (-) ARChrono par jour affiché par le chronocomparateur. On suppose que le chronocomparateur affiche que la pendule avance de 12mn16s sur 24H00 ce qui fait ARChrono=736 secondes.
Pour que la pendule affiche la même heure que le temps de référence, il aurait fallu qu'elle fasse plus de battements (si elle retarde) ou moins de battements (si elle avance) que la valeur que l'on a choisie. Le ratio entre la valeur réelle et la valeur choisie vaut :
Ratio=Dureemesure/(Dureehorloge-ARChrono)
Il faut prendre en compte l'avance/retard ARChronoaffiché par le chronocomparateur. Si le chronocomparateur considère que la pendule avance par rapport au battement choisi, il faut retirer ce temps (sur 24H00). Il faut l'ajouter si le chronocomparateur considère que a pendule retarde.
Avec les valeurs prises en exemple, Ratio=86580/(85920-736)=1,01638805
A partir de cette information, on peut calculer la durée réelle d'un battement DureeBat qui vaut donc :
BatHeure=BatHeureApprox x Ratio
Avec les valeurs prises en exemple, BatHeure = 4250,5 x 1,01638805 = 4320,15
Evidemment, il faut tenir compte du fait que les valeurs mesurées entre l'horloge et la référence de temps sont à +/-1mn de chaque côté ce qui introduit une incertitude dans le résultat. Néanmoins, le réglage au chronocomparateur de l'horloge utilisé pour l'exemple donne des résultats proches de la valeur nominale (la valeur pour cette horloge était effectivement 4320).
Vous trouverez ici une petite feuille Excel pour faciliter les calculs. Les valeurs par défaut sont celles de la pendule prise en exemple.
Une méthode plus simple
Pour les personnes pressées, il y a plus simple que la méthode précédente. On la reprend en partie jusqu’à noter la différence de temps entre le temps de référence (une montre à quartz par exemple) et l’horloge à régler. Supposons que cette différence soit égale à DiffRef sur 24H00. Par ailleurs, on lit la valeur de l’avance-retard ARChrono (également sur 24H00) sur le chronocomparateur.
Si on pose ARvisé = -ARChrono+DiffRef, alors il suffit de régler la position de la lentille du balancier jusqu’à ce que le chronocomparateur affiche ARvisé dans la rubrique « avance-retard ».
Quelques exemples numériques (les avances sont notées avec un signe +, les retards avec un signe -) :
| DiffRef | ARchrono | ARvisé |
| +8mn | -2mn10s |
ARvisé=-8mn-2mn10s=-10mn10s Comme la pendule avance de 8m, il faut la faire retarder de 8mn. Mais comme le chronocomparateur indique qu’avec le battement courant, elle retarde de 2mn10s, alors la pendule sera bien réglée lorsqu’on lira -10mn10s sur le chronocomparateur. |
| -8mn | +2mn10s |
ARvisé=8mn+2mn10s = +10mn10s Comme la pendule retarde de 8m, il faut la faire avancer de 8mn. Mais comme le chronocomparateur indique qu’avec le battement courant, elle avance de 2mn10s, alors la pendule sera bien réglée lorsqu’on lira +10mn10s sur le chronocomparateur. |
| -8mn | -2mn10s |
ARvisé=8mn-2mn10s = +5mn50s Comme la pendule retarde de 8m, il faut la faire avancer de 8mn. Mais comme le chronocomparateur indique qu’avec le battement courant, elle retarde de 2mn10s, alors la pendule sera bien réglée lorsqu’on lira +5mn50s sur le chronocomparateur. |
| +8mn | +2mn10s |
ARvisé=-8mn+2mn10s = -5mn50s Comme la pendule avance de 8m, il faut la faire retarder de 8mn. Mais comme le chronocomparateur indique qu’avec le battement courant, elle avance de 2mn10s, alors la pendule sera bien réglée lorsqu’on lira -5mn50s sur le chronocomparateur. |
Ensuite, afin de connaitre la valeur du battement, il sera possible de régler le battement du le chronocomparateur par dichotomie jusqu'à ce que l'AR affiché soit nul, voire, utiliser une commande du chronocomparateur qui calcule automatiquement la valeur du battement pour obtenir un AR nul.
.
Capteurs pour les mesures
Le chronocomparateur PC-RM4 permet sans modification d'utiliser divers capteurs pour les mesures.
Un capteur piezo très simple
Le plus simple à faire est un capteur piezo que l'on peut fixer directement sur la pendule par une pince crocodile.
A l'oscilloscope, le signal est très net. Avantage, il s'agit d'un capteur peu coûteux (1 ou 2€ ?)
Cliquez sur la vignette pour avoir plus de précisions sur ce capteur.

Un capteur optique (très compliqué)
On peut aussi réaliser un capteur optique. Dans le cas présent, une photodiode est occultée à chaque fois que le balancier passe devant elle. La source lumineuse est un laser ce qui permet d'avoir un faisceau très fin compatible avec la largeur des tiges de balancier.
Cliquez sur la vignette pour avoir plus de précisions sur ce capteur qui est dédié aux mouvements de Paris.
Un autre capteur optique (plus simple)

Ce capteur optique reprend le principe du précédent mais est beaucoup plus simple à réaliser si l'on dispose d'une imprimante 3D et n'est pas dédié à un mouvement particulier. Comme le précédent, une photodiode est occultée à chaque fois que le balancier passe devant elle. La source lumineuse est un laser ce qui permet d'avoir un faisceau très fin compatible avec la largeur des tiges de balancier.
Cliquez sur la vignette pour avoir plus de précisions sur ce capteur.
CHRONOCOMPARATEURS
Les chronocomparateurs décrits ci-après sont visibles sur ce site et peuvent facilement être réalisés par un amateur. Tous les schémas et logiciels sont publiés sur les pages correspondantes.
Le chronocomparateur PC-RM4
Malgré des performances très supérieures à PC-RM1 ou PC-RM3, son prix est du même ordre de grandeur que PC-RM3 (disons, entre 50€ et 100€ selon ce que vous avez en stock chez vous).
Le chronocomparateur PC-RM4 permet de mesurer la différence entre la durée d’un Tic et d’un Tac, la durée d’une Tic et d’un Tac et les valeurs moyennes de ces durées sur l’ensemble de la mesure. Il estime également l’avance et le retard par jour de la montre en fonction de ces durées. Enfin, il peut calculer l'amplitude du balancier.
Il affiche également l’évolution des durées des Tic et des Tac sous forme graphique. Cette possibilité permet de détecter d’éventuelles anomalies de fonctionnement, comme par exemple, une irrégularité des durées qui serait périodique.
Cet affichage graphique permet également de se rendre compte immédiatement de l’impact d’un réglage ou des différences de fonctionnement en fonction de la position de la montre.
Il propose une fonction « oscilloscope » qui permet de visualiser le signal transmis par le capteur ce qui peut faciliter la détection d’anomalies. C'est dans cette fonction qu'est affichée l'amplitude du mouvement.
Il dispose d'une entrée pour des capteurs non-amplifiés (typiquement, des capteurs piezo) et d'une entrée pour capteurs amplifiés. Une alimentation de 5V est fournie sur cette entrée pour ces capteurs. Pour avoir des idées de capteurs pouvant être plus ou moins facilement fabriqués, voir la page sur PC-RM2.
La résolution de chaque mesure est de 25ns. Dans le cas le plus défavorable, la résolution sur 24heures est de l’ordre de 21ms par jour pour une montre qui bat à 18000 coups par heure.
Le chronocomparateur PC-RM5 (pour horloges)
Ce chronocomparateur a été conçu pour faciliter le réglage des horloges à balancier. Son prix est très abordable (de l'ordre de 20 à 30€ en 2023) et il est très simple à réaliser.
Sa précision est moins élevée que celle de PC-RM4 mais elle est plus que suffisante et sa facilité d'utilisation fait qu'aujourd'hui, c'est celui que j'utilise pour le réglage des horloges à balancier.
Il n'y a qu'un seul écran et quelques fonctions permettant de mesurer la période courante du balancier, la comparer à une valeur de réference (que l'on peut saisir) et il est en mesure d'afficher la période mesurée, la différence entre un aller et retour et l'avance-retard sur 24H00.
Il utilise des capteurs optiques (laser ou infra-rouge) dont vous trouverez plusieurs réalisation sur cette page.
Le chronocomparateur PC-RM1
 Le chronocomparateur PC-RM1 permet de mesurer la différence entre la durée d’un Tic et d’un Tac, la durée d’une Tic et d’un Tac et les valeurs moyennes de ces durées sur l’ensemble de la mesure. Il estime également l’avance et le retard par jour de la montre en fonction de ces durées.
Le chronocomparateur PC-RM1 permet de mesurer la différence entre la durée d’un Tic et d’un Tac, la durée d’une Tic et d’un Tac et les valeurs moyennes de ces durées sur l’ensemble de la mesure. Il estime également l’avance et le retard par jour de la montre en fonction de ces durées.
Pour synchroniser PC-RM1 sur T1, réglez la sensibilité au minimum puis augmentez la lentement jusqu’à avoir un battement régulier des diodes luminescente. À ce moment, il est probable que vous êtes synchronisé sur T3. Continuez à augmenter la sensibilité tant que les diodes clignotent régulièrement. Si elles se mettent à clignoter erratiquement, revenez en arrière jusqu’à ce qu’elles clignotent de nouveau régulièrement. Vous êtes alors probablement synchronisé sur T1.
Notez que PC-RM1 dispose d’une fenêtre d’occultation fixe de 50ms (ajustable par matériel). Une fois que vous êtes synchronisé sur T1, tous les chocs se produisant durant les 50ms suivantes (en particulier, T2 et T3) ne sont pas pris en compte. 50ms est une valeur qui est adaptée aux montres « lentes » (18000 battements par heure) et aux montres rapides jusqu’à 36000 battements par heure.
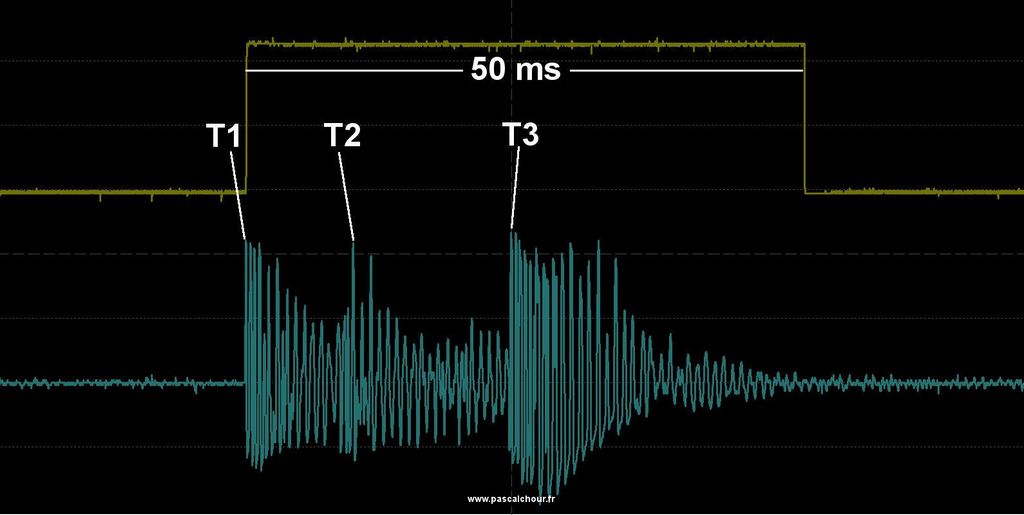
Signal bleu : signal de la montre
Signal jaune : signal généré pour le chronocomparateur
La résolution de chaque mesure est de 4µS. Dans le cas le plus défavorable, la résolution sur 24heures est de l’ordre de 3,45s par jour pour une montre qui bat à 18000 coups par heure.
Si vous avez le choix, fabriquez plutôt PC-RM4. Mais PC-RM1 reste intéressant du fait de sa simplicité de réalisation même si la précision (dans le pire des cas) peut laisser à désirer.
Le chronocomparateur PC-RM3 (obsolète)
Anciens chronocomparateurs
Ce site présente également deux anciens chronocomparateurs que j'ai eu l'occasion de réparer :
- Un vibrograf B200, appareil d'une très grande qualité de fabrication,
- Un Bandelin Tickoprint Transistor TA.