Numérisation des cours Alain PASQUET, Mise en page Pascal CHOUR - 2018-2021
La MÉTROLOGIE est la science des Poids et Mesures : par la classification méthodique qu’elle ordonne, elle permet de fixer quantitativement toute grandeur ; par la confrontation des mesures qu’elle implique, elle ouvre la voie à la discussion des méthodes de mesures et aux résultats mêmes de ces mesures.
Toute mesure faite avec application doit être analysée puis discutée : la Métrologie qui n’est pas une science jeune se perfectionne cependant chaque jour car sa connaissance est indispensable à "la critique" de tout phénomène.
Pour faire de bonnes mesures, en physique comme en électronique, il n’est peut-être pas nécessaire de connaître et d’observer les conventions admises en matière de langage et de SYMBOLES ; la pratique montre cependant que ces conventions sont utiles et qu’il est à la fois plus simple et plus profitable de les connaître et de les observer que de les ignorer et de les enfreindre.
Les décisions de portée internationale concernant les systèmes d’unités sont prises par le COMITÉ INTERNATIONAL DE POIDS ET MESURES ; un organisme permanent de travail, le Comité consultatif des Poids et Mesures assure l’administration des systèmes d’unités et prépare les sessions du Comité International : c’est lui qui propose des programmes aux divers Laboratoires Nationaux de Métrologie.
GRANDEURS PHYSIQUES
Toute grandeur mesurable s’évalue au moyen de deux éléments :
- L’UNITÉ qui est une grandeur connue, de même nature que celle à évaluer
- La VALEUR NUMÉRIQUE : le nombre de fois qu’il faut prendre l’unité pour obtenir la grandeur considérée.
Toutes les grandeurs physiques peuvent être évaluée à l’aide des trois unités de : LONGUEUR, MASSE, TEMPS, qui s’appellent UNITÉS FONDAMENTALES et ont respectivement pour symboles les lettres "L", "M", "T". On appelle UNITÉS DÉRIVÉES toutes les autres. On aura donc à définir autant d’unités qu’il y a d’espèces différentes de grandeurs à évaluer.
Pour l’étude de phénomènes électriques, il faut donc utiliser des grandeurs appropriées : tension, courant, etc…
Les unités de mesures peuvent être arbitraire ; ainsi par exemple pour les longueurs on a différentes unités : en Europe, on utilise le mètre ; dans les pays anglo-saxons, le pouce, le pied. De même pour les volumes : il y a le litre, le mètre cube, le pouce cube, etc… ou le gallon.
Toutes ces différentes grandeurs se trouvent néanmoins liées entre elles par des RELATIONS MATHÉMATIQUES dans lesquelles il suffit de fixer quelques unités, de façon qui peut être arbitraire, pour calculer à partir d’elles toutes les autres. Par exemple la surface "S" d’un carré est donnée par "S = L2", et le volume "V" d’un cube par "V = L3", où "L" est toujours la même grandeur considérée, côté du carré ou du cube considéré.
On peut dans ce cas, ayant fixé une fois pour toutes l’unité de longueur (par exemple le mètre), considérer comme unité de surface et de volume l’aire d’un carré et le volume d’un cube ayant un mètre de côté. Ainsi l’unité de surface sera le mètre carré, l’unité de volume le mètre cube.
En fixant encore l’unité de TEMPS et de MASSE, en même temps que l’unité de LONGUEUR, on détermine toutes les unités mécaniques à partir de différentes expressions mathématiques qui définissent les différentes grandeurs.
Par exemple si on choisit comme unité de temps la seconde et comme unité de longueur le mètre, on en déduira l’unité de vitesse à partir de la relation qui la définit, et qui n’est autre que l’espace parcouru divisé par le temps mis à le parcourir, c’est-à-dire :
L’unité de vitesse sera la vitesse pour laquelle l’unité de longueur (mètre) est parcourue pendant l’unité de temps (seconde) : ce sera la vitesse de un mètre par seconde, désignée par "1 m/s", ou "1 m . s-1".
Si au contraire on avait pris comme unité de longueur le kilomètre et comme unité de temps l’heure, on aurait trouvé comme unité de vitesse le kilomètre/heure.
En poursuivant le raisonnement dans ce sens, on définira toutes les unités électriques pourvu que, outre les unités fondamentales déjà vues (longueur, temps, masse ou force), on se donne encore une unité électrique quelconque, soit de résistances, de courant ou de tension.
Un SYSTÈME D’UNITÉS de mesure est précisément l’ensemble de toutes les unités obtenues quand on a fixé QUATRE UNITÉS FONDAMENTALES : il est évident qu’il y aura un grand nombre de système d’unités de mesure puisqu’on peut choisir un nombre très varié de combinaisons d’unités fondamentales.
Le premier système adopté, d’emploi encore universel pour les usages scientifiques, est le système "C.G.S." dont les unités fondamentales sont le CENTIMÈTRE "C", le GRAMME "G", et la seconde "S".
L’unité de vitesse sera le "cm." par seconde, c’est-à-dire l’unité de longueur parcourue par l’unité de temps.
L’unité d’accélération est le "cm/sec/sec" ou "cm . sec-2", accélération d’un mobile dont la vitesse s’accroît de "1 cm/sec." par seconde.
L’unité "C.S.G." de force s’appelle DYNE ; la formule "f = mγ" fournit sa définition : c’est la force qui, agissant sur une masse d’un gramme, lui implique une accélération de "1 cm/sec/sec".
L’unité "C.G.S." de travail est l’ERG : c’est le travail fourni par une force de 1 dyne quand celle-ci déplace son point d’appui de 1 centimètre dans sa direction. L’unité PRATIQUE est le JOULE valant 10.000.000 ergs.
L’unité "C.G.S." de puissance est l’ERG PAR SECONDE, puissance d’un moteur qui fournit un travail d’un erg par seconde. L’unité PRATIQUE est le WATT qui n’est autre que le joule par seconde, et vaut 10.000.000 ergs par seconde.
Connaissant ainsi les dimensions correspondantes, TOUTES LES AUTRES UNITÉS DÉRIVÉES sont faciles à définir.
Suivant que l’on fixe comme unité électrique la perméabilité électrostatique ou la perméabilité électromagnétique dans le vide, le système "C.G.S." s’étend aux systèmes des unités électriques dits, soit SYSTÈME ÉLECTROSTATIQUE "C.G.S." (en abrégé : "E.S.C.G.S."), soit SYSTÈME ÉLECTROMAGNÉTIQUE "C.G.S." ("E.M.C.G.S.").
Mais tout système pour être utilisé rationnellement doit être PRATIQUE, or les unités "C.G.S." s’adaptent mal à la mesure des phénomènes courants. C’est pourquoi on a adopté un autre système, appelé SYSTÈME GIORGI du nom de son inventeur. Bien que le système Giorgi n’ait pas encore été officiellement imposé par le Comité international des Poids et Mesures, il est en pratique, actuellement généralisé ; ses trois unités fondamentales qui sont le MÈTRE, le KILOGRAMME et la SECONDE étant d’emploi le plus courant.
Pour faciliter leur usage, certaines unités des systèmes ont reçu des noms particuliers. En toute rigueur on pourrait se contenter de baptiser les unités fondamentales mais cela entraînerait des appellations compliquées pour certaines unités dérivées.
Pour plus de commodité, ces noms sont souvent écrits de manière abrégée ; noms et abréviations ont fait l’objet de normalisations internationales.
Les noms d’unités proviennent soit de racines grecques ou latines (par exemple mètre, seconde), soit de noms propres de physiciens illustres (par exemple Volt, Ampère). Les abréviations des premiers sont toujours constituées par une ou plusieurs lettres minuscules de l’alphabet latin ou grec (par exemple "m", "s"), celles des seconds par des majuscules latines ou grecques (par exemple "V", "A").
Dans certains cas particuliers, on fait un emploi systématique de MULTIPLES ou SOUS-MULTIPLES de certaines unités.
Aussi a-t-on défini des coefficients multiplicateurs par des PUISSANCES POSITIVES OU NÉGATIVES ENTIÈRE DE 10 : le tableau de la Fig. 1 en donne la liste avec les abréviations correspondantes et les valeurs du coefficient multiplicateur.
| Téra | T | 1012 |
| Giga | G | 109 |
| Méga | M | 106 |
| Myria | ma | 104 |
| Kilo | K | 103 |
| Hecto | h | 102 |
| Déca | da | 101 |
| Déci | d | 10-1 |
| Centi | c | 10-2 |
| Milli | m | 10-3 |
| Micro | µ | 10-6 |
| Nano | n | 10-9 |
| Pico | p | 10-12 |
| Fig. 1 | ||
Les SYMBOLES des principales unités, suivant le type de mesure intéressé, sont les suivants :
UNITES GEOMETRIQUES
| Longueur | mètre micromètre ou micron |
m µ (ou mu) |
| Surface | mètre carré are |
m2 a |
| Volume | mètre cube stère litre |
m3 st l |
| degré d'angle | d ou ° | |
| minute d'angle | ' | |
| seconde d'angle | " | |
| angle droit | D | |
| grade | gr ou G | |
| radian | rd |
UNITES MECANIQUES
| Masse | gramme tonne sthère |
g t sh |
| Force | newton | n |
| Pression | pièze bar |
pz b |
| Travail | joule | J |
| Puissance | watt | W |
| Seconde de temps | s | |
| minute de temps | mn ou m | |
| heure | h | |
| hertz | Hz | |
| période par seconde | p/s | |
| cycle par seconde | c/s |
UNITES ELECTRIQUES
| Ohm | Ω | |
| siemens | s | |
| mho | Ω-1 | |
| volt | V | |
| ampère | A | |
| ampère tour | At | |
| coulomb | C | |
| farad | F | |
| henry | H | |
| weber | Wb |
UNITES THERMIQUES
| degré Celsius (degré centésimal) |
°C | |
| thermie | th | |
| frigorie | fg |
UNITES OPTIQUES
| candela | cd | |
| lumen | lu | |
| lux | lx | |
| phot | ph | |
| dioptrie | δ (delta) |
UNITES DE TRANSMISSION
| bel | B | |
| néper | N |
UNITES MONETAIRES
| franc | fr | |
| nouveau franc | NF |
Ayant vu ainsi la nécessité d’emploi d’unités cohérentes dans chaque système, nous examinerons dans la prochaine leçon de Métrologie le SYSTÈME GIORGI d’emploi courant et les unités, multiples et sous-multiples, qui le définissent.
SYSTÈME D’UNITÉS PRATIQUES
Nous avons vu précédemment que les systèmes "C.G.S." donnaient naissance à des unités dont l’ordre de grandeur était peu pratique notamment pour la tension et l’intensité.
Ceci correspond au fait que les phénomènes électrostatiques ont un ordre de grandeur notable pour les tensions élevées, et que les phénomènes électromagnétiques ont un ordre de grandeur notable pour les courants intenses.
Le SYSTÈME GIORGI, présente dans les formules des coefficients d’un ordre de grandeur qui rend commodes les calculs.
Nous avons déjà dit que ses trois unités fondamentales étaient le mètre, le kilogramme et la seconde.
UNITÉS FONDAMENTALES ÉLECTRIQUES
Les trois unités ci-dessus sont complétées par deux unités fondamentales électriques, qui ne sont autres que des étalons de mesures :
- L’OHM INTERNATIONAL qui est la résistance à 0° C d’une colonne de mercure ayant une masse de 14,4521 g, longue de 106,300 cm et de section constante (voisine de 1 mm2). L’ohm international moyen a pour valeur 1,00049 ohm.
- L’AMPÈRE INTERNATIONAL qui est l’intensité d’un courant constant qui, traversant une solution aqueuse d’azote d’argent, dépose 1,118 mg de métal par seconde. L’ampère international moyen a pour valeur 0,99985 ampère.
Ces valeurs sont, comme leur nom le rappelle, les valeurs moyennes des ÉTALONS INTERNATIONAUX conservés dans les différents pays. Ainsi pour la France seule, les valeurs des unités internationales sont respectivement 1,000506 et 0,999842.
PRINCIPALES UNITÉS ÉLECTRIQUES
Les principales unités électriques du système Giorgi, unités d’emploi courant sont :
| L'AMPERE | Unité de COURANT – c’est le courant continu qui parcourant deux conducteurs rectilignes et parallèles détermine une attraction entre eux de 2.10-7 newton par mètre de longueur des conducteurs. Rappelons que le NEXTON "N", unité de force du système Giorgi, est la force qui appliquée à une masse de 1 |
| LE VOLT | Unité de TENSION – c’est la différence de potentiel (ou chute de tension) qui s’établit aux bornes d’un conducteur parcouru par 1 Ampère quand est dissipé une puissance de 1 Watt. Rappelons que le Watt "W", unité de puissance du système Giorgi, est la puissance fournissant le travail de 1 Joule (unité de travail) en 1 seconde. |
| L’OHM | Unité de RÉSISTANCE – c’est la résistance d’un conducteur aux bornes duquel on mesure une chute de tension de 1 Volt quand il est parcouru par 1 Ampère. |
| LE COULOMB | Unité de QUANTITÉ D’ÉLECTRICITÉ – c’est la quantité d’électricité qui traverse en 1 seconde la section d’un conducteur parcouru par 1 Ampère. C’est aussi la capacité d’un condensateur dont chaque armature prend l’unité de quantité d’électricité (ou charge électrique) quand on soumet ce condensateur à la différence de potentiel unité. |
| LE FARAD | Unité de CAPACITÉ – C’est la capacité d’un condensateur qui, placé sous une tension de 1 Volt emmagasine une charge de 1 Coulomb. |
| LE HENRY | Unité d’INDUCTANCE – c’est l’inductance (propre) d’un circuit qui parcouru par un courant variant à raison de 1 Ampère par seconde, est le siège d’une force électromotrice d’induction (ou tension) (propre) égale à 1 Volt. |
| LE WEBER | Unité de FLUX d’INDUCTION MAGNÉTIQUE – C’est le flux qui, traversant une spire et ramené à la valeur nulle en une seconde, détermine aux bornes de la spire une force électromotrice (tension) de 1 Volt. |
Ce sont donc les principales unités auxquelles on a donné un nom ; les autres unités n’ont pas de nom propre, mais sont définies selon les relations dont elles découlent.
Ainsi par exemple l’unité de vitesse est, nous l’avons déjà vu, le "mètre par seconde" ; l’unité d’induction est le "Weber par mètre carré" ; l’unité de perméabilité magnétique est le "Henry par mètre" ; l’unité d’intensité de champ est le "Volt par mètre" ; l’unité de résistivité est l’"Ohm . mètre" etc…
A ce propos rappelons que "par" signifie : divisé par.
Au contraire le signe "." signifie : multiplié par.
Ainsi "Ohm . mètre" signifie : Ohm x mètre.
Toutes les unités découlent donc de relations qui les lient les unes aux autres, ce sont les équations dites de définition dont nous allons rappeler les principales.
FORMULES ESSENTIELLES :
| Loi d’Ohm | U = R.I |
| Loi d’Ohm généralisée | U = Z.I |
| Résistance d'un conducteur homogène | R = ρ.λ/s |
| Puissance consommée par une résistance | P = U.I |
| Loi de capacité | Q = C.U |
| Capacité d'un condensateur plan | C = (ξ.s) / (4.π.λ) |
| Induction électrique | D = ξ.s |
| Energie d'un condensateur chargé | W = ½.C.U2 = ½.Q2/C |
| Densité d'énergie dans un champ électrique | DE = ½.(E.D)/(4.π) |
| Flux magnétique et inductance | nΦ = L.I |
| Inductance d'une bobine longue | L = 4.π.n2.(µ.S)/λ |
| Induction magnétique | β = µ.H = Φ/s |
| Force magnétomotrice | F = 4.π.I |
| Intensité d'un champ magnétique dans une bobine longue | H = 4.π.n.I/λ |
| Energie d'une inductance parcourue par un courant | W = ½.L.I2 |
TABLE DU SYSTÈME GIORGI
Ayant préalablement défini au moins quatre unités fondamentales, nous pouvons nous servir maintenant des relations précédentes pour déterminer les unités de mesures du système Giorgi.
Les tableaux suivant donnent :
- le nom de la grandeur
- son symbole
- l’équation de définition
- l’unité de mesure propre
- l’abréviation de l’unité.



MULTIPLES ET SOUS-MULTIPLES :
Enfin, pour terminer avec ces notions générales sur les systèmes d’unités et le système Giorgi en particulier, dont il est indispensable d’avoir une connaissance précise si l’on veut être capable de faire des mesures, nous indiquons qu’il est souvent nécessaire d’introduire dans le calcul des multiples et sous multiples. Par exemple le volt est trop grand pour mesurer la tension induite dans une antenne, et il est trop petit pour mesurer la haute tension des lignes de transport d’énergie : dans le premier cas le millivolt ou le microvolt sont plus pratiques, dans le second cas ce sera le kilovolt.
Multiples et sous-multiples s’obtiennent en plaçant devant le nom de l’unité les préfixes que nous avons déjà vus à la leçon précédente et en la multipliant par le coefficient indiqué qui est une puissance positive ou négative de 10.
| Ainsi, pour les mesures de capacité, pourra-t-on choisir : | ||
| Le picofarad | pF | 10-12 F |
| (ou le micromicrofarad) | µµF | 10-6 x 10-6 = 10-12 F |
| Le nanofarad | nF | 10-9 F |
| (ou le kilopicofarad) | kpF | 103 x 10-12 = 10-9 F |
| Le microfarad | µF | 10-6 F |
| Le milifarad | mF | 10-3 F |
Pour les mesures de résistances, on aura : |
||
| Le kilohm | kΩ | 103 Ω |
| Le Mégohm | MΩ | 106 Ω |
Nous verrons au cours de la prochaine leçon les qualités requises pour une bonne mesure, ainsi que les natures d’erreurs qui peuvent influer sur le résultat.
MÉTHODES DE MESURES
Toute mesure, c’est-à-dire toute détermination de la mesure d’une grandeur, aboutit en dernière analyse à la perception d’un certain nombre de sensations repérables fournies par les organes entrant dans la composition du dispositif de mesure. Ces organes peuvent être classés en deux catégories suivant qu’ils donnent des sensations repérables toutes INDÉPENDANTES ou NON de leur insertion dans un dispositif de mesure. La première catégorie est celle des grandeurs étalonnées, la seconde est celle des appareils de mesure : nous étudierons cette dernière catégorie ultérieurement en détail ; voyons la première.
GRANDEURS ETALONNÉES
Une grandeur étalonnée parfaite est une grandeur dont la mesure ne dépend que des SENSATIONS repérables qu’elle donne. On peut donc définir pour un tel organe une sensation globale dont le repère peut être confondu avec la mesure de la grandeur étalonnée.
Malheureusement on ne sait pas réaliser de telles grandeurs étalonnées : celles que l’on construit sont des grandeurs qui dépendent peu, mais en dépendent tout de même, de l’intensité des phénomènes qu’elles mesurent ainsi que des conditions du milieu ambiant dans lequel elles sont plongées.
La mesure déduite des sensations repérables données par une telle grandeur est la mesure ORIGINALE de la grandeur : elle devra tout normalement être corrigée en fonction des considérations précédentes. Ainsi par exemple la mesure d’une résistance étalonnée réglable dépend non seulement de la position des commutateurs de réglage, mais encore de l’intensité du courant qui la parcourt, de la fréquence de ce courant, de la température ambiante, du vieillissement des matériaux etc… Les précautions prises à sa construction permettent d’affirmer que moyennant le bon entretien de cet organe et son utilisation dans un domaine limité d’intensités, de fréquences, de températures, etc… La mesure de sa résistance éventuellement corrigée sera voisine de la mesure effective.
MÉTHODES DE MESURES
Selon la MANIÈRE dont la mesure inconnue de la grandeur mesurée est liée aux mesures effectives ou indiquées par le dispositif de mesure on classe généralement les méthodes de mesure en deux grandes catégories.
1 – Méthodes de déviation :
Supposons qu’on veuille mesurer une résistance inconnue "x" et qu’on dispose d’une résistance étalonnée "ρ", variable de façon connue. Plaçons les deux résistances en série dans un circuit commun (Fig. 1). Ajustons la valeur de la résistance étalonnée de manière qu’un voltmètre connecté, tantôt aux bornes de la résistance "x" tantôt aux bornes de la résistance "ρ" accuse la même déviation.
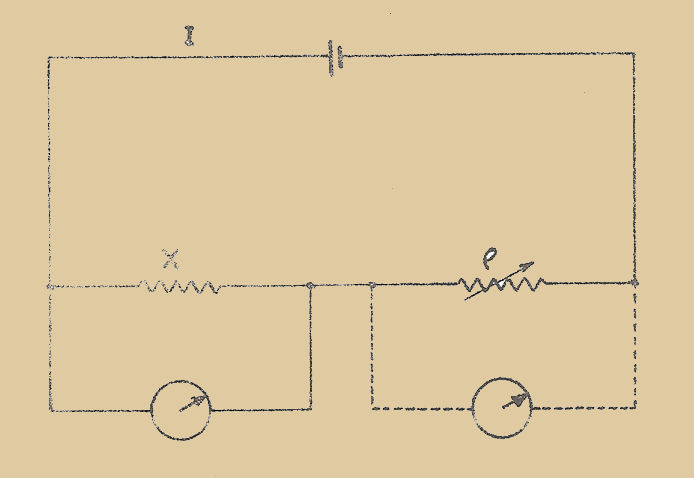
Fig. 1
Lorsqu’après quelques tâtonnements cette condition est réalisée, les deux résistances "x" et "ρ" sont égales. La méthode de déviation consiste donc à faire en sorte qu’un même appareil accuse LA MÊME DÉVIATION dans deux phases nécessaires de la mesure.
2 – Méthodes de zéro :
Reprenons nos deux résistances "ρ" et "x", cette dernière de valeur inconnue.
Plaçons la résistance inconnue "x" et la résistance étalonnée variable dans deux branches d’un pont de Wheastone complété par deux bras égaux "a" (Fig. 2), et ajustons la résistance réglable "ρ" de manière que le galvanomètre "G" n’accuse aucune déviation. La condition d’équilibre est x = ρ
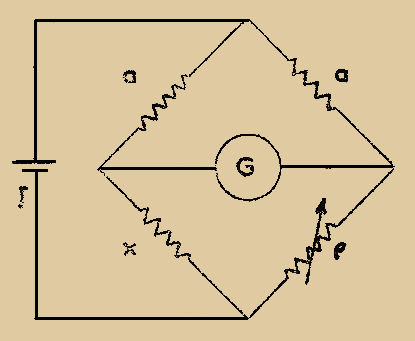
Fig. 2
La méthode de zéro consiste à régler un (ou plusieurs) élément variable d’un montage de manière qu’un instrument indicateur n’accuse AUCUNE DÉVIATION.
Le résultat d’une mesure ne sera donc jamais exactement égal à la mesure effective de la grandeur mesurée, car de nombreuses causes peuvent être à l’origine de ce défaut : ce sont les ERREURS DE MESURE.
NATURE DES ERREURS
Toute mesure étant entachée d’erreurs, il y a lieu de distinguer immédiatement les erreurs SYSTÉMATIQUES des erreurs ACCIDENTELLES.
1 – Erreurs systématiques :
Les erreurs systématiques sont dues aux imperfections des APPAREILS et sont toujours de MÊME SENS : soit en excès (en plus) soit en défaut (en moins).
Dans la pratique, on cherche à les supprimer autant que faire se peut, ou bien l’on en tient compte en corrigeant les résultats, de sorte que l’on n’aura pas à s’en préoccuper dans le calcul d’erreurs proprement dit.
2 – Erreurs accidentelles :
Les erreurs accidentelles sont dues à l’imperfection de nos SENS. Le meilleur procédé pour s’en rendre compte consiste à répéter la mesure de la même grandeur plusieurs fois : si l’on apprécie avec une précision suffisante, on trouvera toutes les fois un résultat DIFFÉRENT.
Ces erreurs sont inévitables : leur caractère est d’être fortuites et indépendantes les unes des autres.
Elles ne répondent à aucune loi.
Toutefois si les mesures sont soignées, l’expérience montre que :
a – Les valeurs affectées d’une légère erreur sont plus NOMBREUSES que celles comportant une erreur grave.
b – Si le nombre des mesures est assez considérable, il y a autant de résultats qui pèchent par DÉFAUT.
Le CALCUL DES PROBABILITÉS conduit à des conclusions analogues.
QUALITÉS D’UNE MESURE
Les indications données ci-dessus au sujet des erreurs permettent de définir les différentes qualités d’une mesure.
JUSTESSE Une mesure est FAUSSE lorsque son résultat est affecté d’une importante erreur SYSTÉMATIQUE ; elle est JUSTE dans le cas contraire.
PRÉCISION Une mesure est PRÉCISE lorsque la limite supérieure de l’erreur ACCIDENTELLE qui affecte son résultat est REDUITE.
Il apparaît dès lors que la notion de précision est une notion toute RELATIVE qui nécessite de distinguer entre l’erreur ABSOLUE d’une grandeur mesurée et son erreur RELATIVE.
ERREUR ABSOLUE ET ERREUR RELATIVE
Dans toute mesure, sachant que le résultat ne peut être parfaitement exact, on recherche donc à déterminer, non point l’erreur elle-même, mais la limite supérieure de cette erreur.
Dire que l’erreur commise sur une mesure "M" est "± e", cela veut dire que la valeur exacte "x" est comprise entre "M + e" et "M - e" : "± e" s’appelle l’ERREUR ABSOLUE commise sur "M".
Dans les applications, il est presque toujours beaucoup plus intéressant de considérer l’ERREUR RELATIVE "Ʃ" ("sigma" majuscule) définie par
On exprime souvent l’erreur relative en POUR CENT :
Cette expression d’erreur relative est très commode : ainsi s’il s’agit de la mesure de la tension du secteur, on dira que la valeur lue diffère de la valeur réelle de 4%, soit 5 Volts pour une tension effective de 125 Volts par contre lors de la mesure de tarage d’une pile étalon on dira par exemple que l’erreur maximum admise est de 0,1 % soit 0,0048 Volt pour une pile de 4,8 Volts.
Si l’on pouvait connaître la valeur de l’erreur effectuée, on pourrait remonter à la valeur exacte de la grandeur mesurée en corrigeant le résultat obtenu par la lecture sur l’appareil.
Ceci est en pratique impossible car on ne sait pas si l’erreur commise est en plus ou en moins, c’est-à-dire si la valeur lue est plus grande ou plus petite que la valeur réelle.
On cherchera donc à examiner attentivement les différentes causes d’erreurs ou tout au moins à savoir la PLUS GRANDE VALEUR possible de l’erreur commise, c’est-à-dire à pouvoir déterminer l’IMPRÉCISION avec laquelle la mesure a été effectuée.
LES CAUSES D’ERREURS
Une partie des causes d’erreurs amène des erreurs qui sont toujours du même signe, c’est-à-dire qu’elles conduisent à évaluer la grandeur plus grande ou plus petite que la valeur réelle lorsque la même mesure est répétée plusieurs fois : d’autres causes amènent les erreurs à être indifféremment en plus ou en moins.
Les erreurs systématiques peuvent être dues à :
- Un mauvais étalonnage de l’appareil
- Une aiguille mal tarée au zéro
- Un appareil prévu pour fonctionner en position horizontale et placée en position verticale
- Un courant de circulation trop important etc…
Les erreurs accidentelles peuvent être causées par :
- L’influence de la température ambiante sur l’étalonnage de l’appareil
- Une variation dans la tension d’alimentation
- Une erreur de lecture sur l’échelle etc…
Nous terminerons l’exposé de ces notions sur les erreurs dans les mesures, lors de la prochaine Leçon de Métrologie, et nous parlerons des appareils indicateurs, organes essentiels des mesures.
ESTIMATION DES ERREURS
En pratique, il est très difficile d’estimer jusqu’à quel point l’erreur commise est due à une erreur systématique ou accidentelle ; et n’apparaissent pas toujours comme évidentes les erreurs systématiques même notables, parce que précisément elles sont toujours commises de la même façon.
Un opérateur qui mesure des longueurs en utilisant un mètre trop long trouve SYSTÉMATIQUEMENT des nombres trop petits. De même un opérateur qui mesure les puissances au moyen d’un wattmètre en négligeant de tenir compte de la consommation propre de cet appareil trouve SYTÉMATIQUEMENT des nombres trop grands.
Ces erreurs systématiques sont dues à des imperfections des étalons, des instruments ou des méthodes de mesure.
Pour estimer la grandeur de l’erreur systématique, autant que faire se peut, il n’y a rien d’autre que de multiplier les mesures avec des appareils différents, en utilisant des méthodes différentes, tout en perfectionnant appareils et méthodes.
Par contre, les erreurs accidentelles obéissant aux lois du calcul des probabilités sont avec une égale probabilité, tantôt positives, tantôt négatives : on pourra donc en évaluer la grandeur, étant bien évident que si on multipliait les mesures à l’INFINI, L’ERREUR MOYENNE GÉNÉRALE SERAIT NULLE.
Voyons par exemple l’erreur qui peut être commise à la lecture sur l’échelle de l’appareil, en dehors de toute méthode de mesure ou précision de l’instrument ; il y a une erreur de lecture, que l’on appelle L’ERREUR DE PARALLAXE, due uniquement à l’opérateur et pouvant amener à des résultats très différents de la vraie valeur.
L’erreur de parallaxe provient de ce que l’observateur n’opère pas sa lecture dans un plan passant par l’aiguille et rigoureusement perpendiculaire au plan de l’échelle : en effet l’aiguille se trouvant à une certaine distance de l’échelle on constate (Fig. 1) que l’œil de l’observateur se trouvant soit en "B", soit en "C", voit l’aiguille projetée sur des points différents de l’échelle, et on lit des valeurs "B" et "C" différentes de la vraie valeur "A".
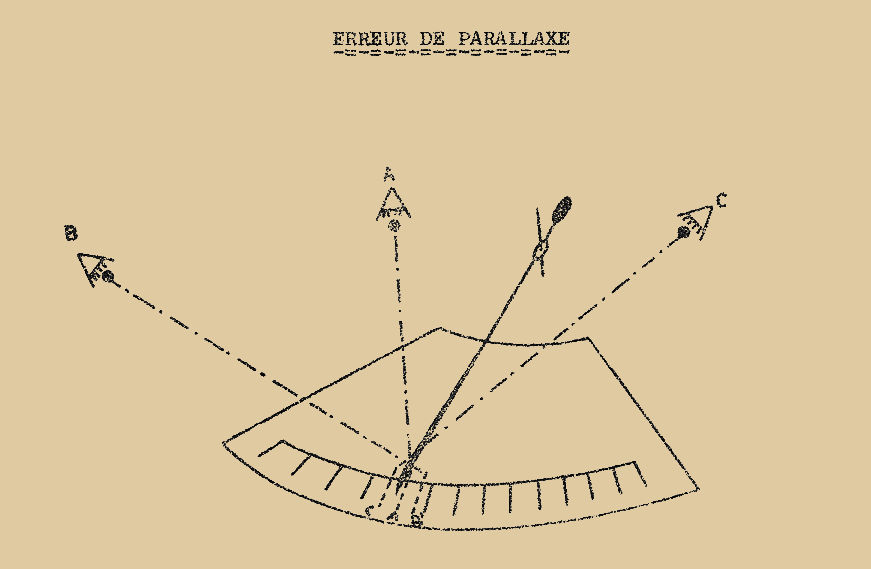
Fig. 1
Il faudra donc faire la lecture avec un seul œil en cherchant à être dans la direction perpendiculaire au plan de l’échelle passant par l’aiguille (point "A").
Cette erreur banale a une importance non négligeable puisqu’elle peut facilement atteindre quelques pourcentages ; c’est pourquoi dans les appareils de haute précision on place le long de l’échelle un miroir dans laquelle se réfléchit l’image de l’aiguille ; l’opérateur pour toute lecture se place dans une position telle que l’aiguille et son image soient confondues.
LE CALCUL D’ERREURS
Les erreurs accidentelles étant de sens quelconque, on peut s’en affranchir partiellement en faisant la MOYENNE des résultats "R1", "R2", …"Rn" de "n" mesures effectuées dans des conditions comparables :
La moyenne ne se justifie que dans le cas où les "n" mesures ont été faites avec le même soin, dans des conditions favorables, inspirant une égale confiance. Appelons "δ" ("delta") la différence entre une valeur quelconque "Rn" et la moyenne "R"
"δ" est à peu de chose près l’erreur du résultat "R"
Proposons-nous de rechercher la valeur moyenne de "δ", c’est-à-dire l’ERREUR MOYENNE de nos mesures. Si nous essayons de chercher la moyenne arithmétique :
Ʃ δ exprime la "somme de δ"
Or, l’expression Ʃ δ/n se trouvera être par définition zéro.
Il a donc fallu définir autrement leur moyenne. On appellera ERREUR MOYENNE "e" des observations ce que l’on pourrait appeler VALEUR EFFICACE des erreurs. C’est la RACINE CARRÉE de la MOYENNE DES CARRÉS DES ERREURS.
L’erreur "E" à craindre sur la moyenne "M" elle-même est la moyenne des erreurs "e", soit :
± √(e2/n) donc E = ± √((Ʃ δ2)/n2)
Cette formule met en évidence l’intérêt D’AUGMENTER LE NOMBRE "n" DES OBSERVATIONS, afin de diminuer l’erreur commise en acceptant comme valeur exacte la moyenne arithmétique des résultats. Il est bon d’ajouter que ce serait perdre son temps que de multiplier à l’infini le nombre "n" des expériences, de façon à réduire la quantité "E" AU-DELA DE LA PRÉCISION jusqu’à laquelle l’appareil de mesure peut être considéré comme exempt d’erreurs systématiques : c’est donc sur cet organe de la mesure qu’il faut porter son attention.
LES INSTRUMENTS DE MESURE
Maintenant que nous avons vu comment on sait faire une mesure en théorie et comment on peut évaluer les erreurs que l’on est susceptible de commettre, nous arrivons à la partie pratique c’est-à-dire aux instruments qui nous servent à opérer.
Nous allons rapidement voir quelles sont les différents types D’APPAREILS INDICATEURS les applications les plus rationnelles et les causes d’erreurs les plus probables.
a – Instruments Indicateurs à bobine mobile :
Ces instruments sont capables de mesurer un courant continu, étant sensibles au sens du courant : c’est-à-dire que l’aiguille se déplace en sens inverse si on inverse la polarité des connexions.
On peut s’arranger pour que l’échelle soit linéaire, donc très simple à tracer. De plus, avec ces appareils, on atteint des sensibilités élevées, et on construit couramment des microampèremètres de 50 microampères pour toute l’échelle, et même moins.
Dans le domaine des mesures de laboratoire on atteint d’excellentes sensibilités avec des galvanomètres : il suffit de penser qu’une graduation de leurs échelles correspond seulement à quelques millièmes de microampère.
La stabilité de réglage de ces appareils est très bonne car pratiquement l’aimant permanent ne se démagnétise pas, et étant donné l’intensité élevée du champ magnétique qu’ils créent dans l’espace environnant la bobine, ils ne sont pas sensibles aux champs magnétiques continus extérieur, donc indépendante du champ magnétique terrestre.
Si la bobine est traversée par un courant alternatif, l’aiguille tend à en suivre les oscillations, bien que restant centrée autour du zéro : cependant dans de tels cas on court le risque de détruire la bobine mobile car on n’a aucune indication sur le courant qui la parcourt.
La consommation de ces appareils comme contrôleurs est en général très réduite, de l’ordre du "mW" ; la chute de tension, qui se produit aux bornes quand l’aiguille est en bout d’échelle, va de quelques "mV" à quelques dixièmes de volt, suivant leur portée.
b – Instruments électrodynamiques :
On sait que ces instruments donnent une indication indépendante du sens du courant alternatif, et qu’en particulier ils donnent de celui-ci la valeur efficace.
Ils sont d’une très grande précision, et s’emploient en général comme des appareils étalons, pour "C.C." et "C.A." indifféremment. Ils ont seulement l’inconvénient d’avoir une échelle quadratique (le déplacement de l’aiguille est proportionnel au carré du courant qui parcourt l’instrument) donc une échelle très resserrée au début.
Ces appareils étalons ont en général deux portées, la première étant double de l’autre, qu’on obtient facilement en mettant les deux bobines (mobile et fixe) en série ou en parallèle.
Leur consommation est notable par rapport à ceux à bobine mobile : ils peuvent donc perturber le fonctionnement du circuit sur lequel ils sont branchés si ce dernier a une impédance élevée comme il arrive dans les circuits radio ; aussi ne sont-ils pas d’usage courant.
Industriellement, les Voltmètres de ce type sont seulement utilisés comme Wattmètre, soit pour "C.C.", soit pour "C.A.".
c – Instruments à Fer Mobile :
Leur construction simple et leur robustesse jointe à la propriété qu’ils ont de mesurer, soit en "C.C.", soit en "C.A." (valeur efficace), les a rendus d’un usage commun comme appareils de tableau, où la puissance absorbée par l’instrument a peu d’importance.
En courant alternatif ils sont commodes pour les fréquences industrielles, cependant qu’à fréquence plus élevée leur emploi est limité par les pertes par Hystérésis des masselottes de fer provoquant le déplacement de l’aiguille (de toute façon ces masselottes doivent être en très bon matériau, avec un cycle d’hystérésis très restreint, et une aimantation résiduelle minime). L’aimantation résiduelle se fait sentir quand l’instrument est utilisé en courant continu ; en effet lorsqu’on coupe le courant les masselottes peuvent rester partiellement aimantées, si bien que l’aiguille ne revient plus exactement à zéro.
Pour éviter des erreurs de mesures dues à cette cause, il est toujours préférable de faire deux lectures successives en inversant le branchement de l’instrument qui sera ainsi parcouru par le courant une fois dans un sens, une fois dans l’autre, et on prendra comme valeur correcte la moyenne des deux valeurs obtenues. La différence entre celles-ci est un indice de qualité de l’appareil, cette différence apparaissant d’autant plus grande que l’appareil est moins bon.
d – Instruments Thermiques :
Ils sont exclusivement utilisés pour des fréquences très élevées auxquelles les autres appareils ne sont plus adaptés. En particulier on utilise les appareils à thermocouple, mais étant donné leur extrême délicatesse, on cherche à en faire usage le moins possible : il suffit en effet d’un courant d’environ une fois et demi celui correspondant à toute l’échelle, pour détruire l’appareil. Les appareils à thermocouple mesurent des valeurs efficaces.
e – Instruments à redresseur :
Étant donné la consommation des instruments "C.A.", soit ceux à fer mobile, soit les appareils électrodynamiques, on utilise pour mesurer les grandeurs alternatives dans la pratique radio, un instrument à bobine mobile muni d’un redresseur, de façon à convertir le "C.A." en "C.C.".
La disposition utilisée communément est celle de la Fig. 2 : quatre redresseurs sont montés en pont de Graetz de façon à redresser ensemble les deux demi-périodes.
Comme on l’a déjà vu cet appareil est capable d’indiquer la valeur moyenne conventionnelle d’une grandeur alternative.
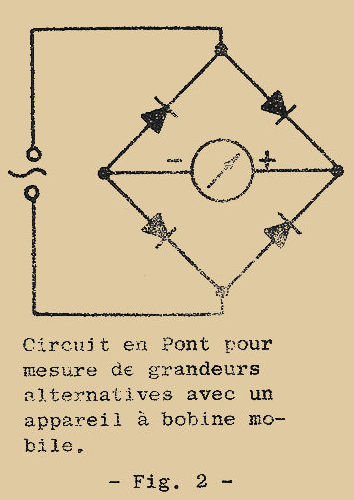
Puisque en pratique la valeur efficace est plus significative ils sont gradués en valeur efficace : cette graduation est seule valable pour des courants sinusoïdaux, puisque la valeur indiquée est la valeur moyenne multipliée par 1,11 ; elle correspond donc à la valeur efficace, seulement pour un courant sinusoïdal.
La résistance du redresseur se trouve être en série avec celle du galvanomètre et puisqu’elle a une valeur qui dépend du courant qui la parcourt, l’échelle n’est pas linéaire mais légèrement contractée à son début.
Utilisés comme milliampèremètres, ils provoquent en général une chute de 2 à 3 V. Aux bornes du redresseur, c’est pourquoi ils perturbent souvent les circuits basse tension sur lesquels ils sont branchés.
Les redresseurs généralement utilisés dans les contrôleurs universels sont du type à oxyde de cuivre et sont valables pour des fréquences jusqu’à 10 ou 20 kHz au plus, c’est-à-dire exclusivement dans le domaine des fréquences acoustiques.
Pour des fréquences élevées il faut utiliser des diodes à vide ou au germanium, dont l’emploi tend aujourd’hui à se généraliser.
Un défaut de ces appareils, outre celui de donner des indications seulement valables pour des formes d’ondes sinusoïdales, est le fait que le redresseur change de caractéristique avec la température ambiante, ce qui change l’étalonnage.
Ces variations font que l’on ne peut pas espérer une précision meilleure que quelques %.
APPAREILS INDICATEURS
Un APPAREIL INDICATEUR est un dispositif capable de donner une indication grâce à laquelle on peut remonter à la valeur de la grandeur que l’on doit mesurer.
Dans le domaine des mesures électriques en particulier un appareil indicateur est pourvu de deux BORNES à relier au circuit sur lequel doivent être exécutées les mesures.
Il est constitué par un ÉQUIPAGE MOBILE, muni d’une AIGUILLE, qui peut se déplacer sur un cadran gradué. Cette graduation est appelée ÉCHELLE et peut être de différents types selon la nature de l’instrument. La graduation peut être en A, mA, V, µV, etc…, de telle sorte que l’indication correspondant à la position de l’aiguille donne directement la valeur de la grandeur mesurée.
Les instruments les plus utilisés [Note : dans les années 1950] sont du type GALVANOMÉTRIQUE, en ce sens que le déplacement de l’aiguille est dû au champ magnétique créé par le courant qui y circule.
Les trois principaux types d’instruments sont : À BOBINE MOBILE, À FER MOBILE, ÉLECTRODYNAMIQUES.
A ces trois types d’instruments, correspondent trois types caractéristiques d’échelles : c’est pourquoi l’instrument peut être reconnu à première vue en observant simplement le cadran.
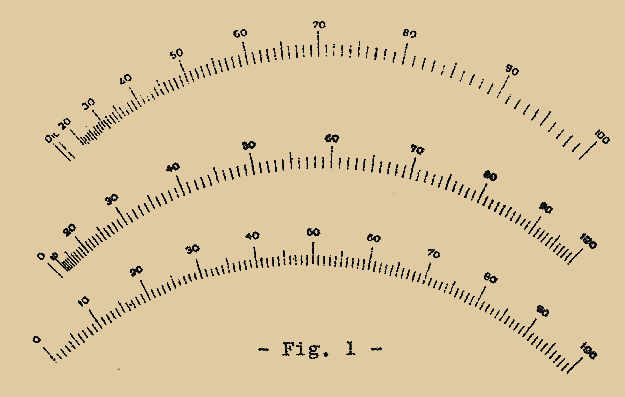
La Fig. 1 représente de bas en haut :
- Une ÉCHELLE LINÉAIRE, caractéristique des instruments à bobine mobile. Le terme linéaire vient du fait que les graduations sont équidistantes sur tout le tracé de l’échelle.
- Une ÉCHELLE DILATÉE, caractéristique des instruments à fer mobile. Comme on peut le voir, les graduations sont contractées au début et à la fin de l’échelle.
- Une ÉCHELLE QUADRATIQUE, caractéristique des appareils électrodynamiques. Ses graduations sont très rapprochées à gauche, alors qu’elles vont vers la droite en s’écartant.
APPAREILS À BOBINE MOBILE
Le dessin d’un équipage mobile est donné Fig. 2 : un petit cadre très léger "T", en aluminium, porte deux axes en acier "P" se terminant en pointe et reposant sur des supports "S" qui peuvent être en acier dans les modèles ordinaires ou en matériau très dur (Rubis) dans les instruments de précision. L’axe supérieur porte perpendiculairement à lui-même, l’aiguille "I" ; comme l’aiguille n’est prolongée que d’un seul côté, il faut qu’elle soit pourvue du côté opposé d’un contrepoids pour l’équilibrer. Deux ressorts de rappel "M", du type à spirale, sont fixés aux deux axes par une extrémité, et à la partie fixe de l’appareil par l’autre extrémité.
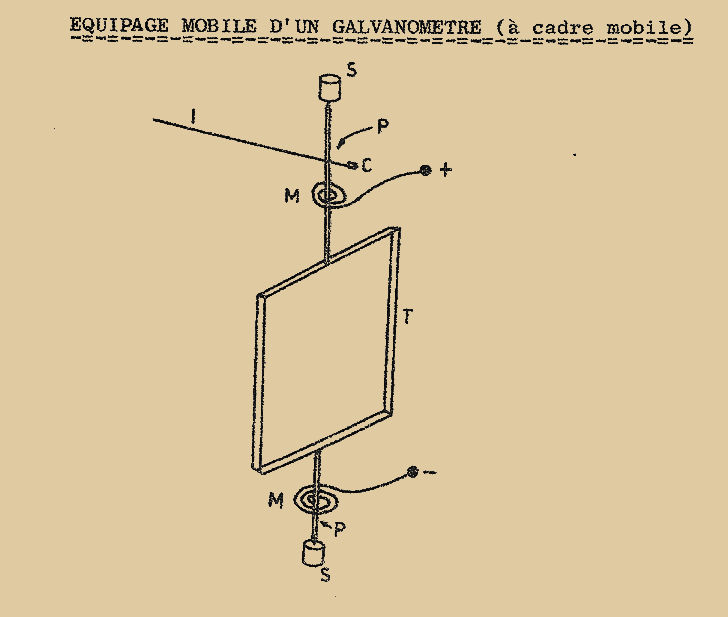
Fig. 2
En général les deux axes sont isolés entre eux, les deux ressorts servent ainsi de conducteurs reliant les deux bornes plus et moins de l’appareil aux extrémités de la bobine faite d’un fil très fin de cuivre émaillé enroulé sur le cadre "T". C’est précisément à cause de cela, et parce que la bobine fait partie de l’équipage mobile, que ces appareils sont dits à bobine mobile.
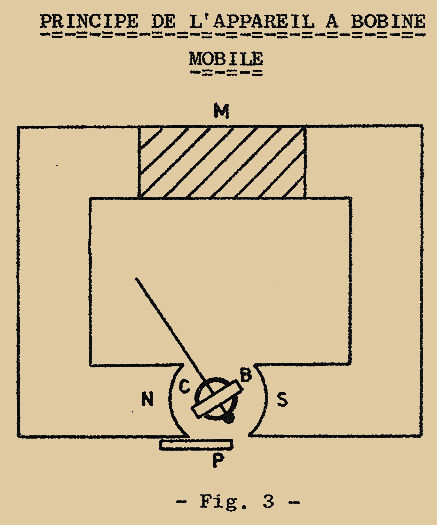
Pour expliquer le FONCTIONNEMENT de cet instrument reportons-nous à la Fig. 3 où l’on voit comment l’équipage mobile est monté entre les deux pôles d’un puissant aimant : la bobine est plongée entièrement dans le champ magnétique créé par l’aimant "M". Si maintenant on fait passer du courant continu dans la bobine, le phénomène d’interaction entre courant et champ magnétique fait naître des forces qui agissent sur la bobine, tendent à la faire tourner autour de son axe. Le sens dans lequel agissent les forces, ou mieux le sens dans lequel agit le COUPLE MOTEUR (l’ensemble de ces forces tendant à faire tourner l’équipage mobile prend le nom de couple moteur), dépend du sens dans lequel circule le courant dans la bobine.
En inversant le sens du courant on change alors le sens dans lequel tend à tourner l’équipage : l’aiguille solidaire de l’équipage tend donc à se déplacer soit à gauche soit à droite.
Au fur et à mesure que l’aiguille se déplace de sa position de repos, c’est-à-dire au fur et à mesure que l’équipage tourne, les deux ressorts qui se tendent produisent des forces qui s’opposent à la rotation (les deux ressorts tendent en effet à ramener l’équipage à la position de repos) : c’est-à-dire qu’il y a naissance d’un COUPLE ANTAGONISTE.
Comme ce couple antagoniste se développe au fur et à mesure que l’aiguille s’éloigne de sa position de repos, c’est-à-dire au fur et à mesure que les ressorts se tendent, lorsque la bobine sera parcourue par un courant l’aiguille se placera sur une position d’équilibre telle que le couple moteur soit parfaitement égal au couple antagoniste.
Cette position d’équilibre est d’autant plus éloignée de la position de repos que le couple moteur est plus fort, donc que le courant qui parcourt la bobine est plus intense, pour un champ donné créé par l’aimant et pour un nombre donné de spires de la bobine.
Une proportionnalité parfaite entre le courant qui parcourt la bobine (c’est-à-dire le courant à mesurer) et le déplacement de l’aiguille s’obtient en plaçant au centre de la bobine "B" un cylindre "C" de fer doux fixé à la carcasse de l’appareil. De cette façon on crée un champ plus intense et plus symétrique par rapport à la bobine, quelle que soit la position de cette dernière.
La sensibilité de l’appareil dépend de l’intensité du champ magnétique et du nombre de spires de la bobine ; comme ces dernières ne peuvent être en nombre très élevé, étant donné les dimensions et la légèreté du cadre, on cherche donc à obtenir des champs intenses.
L’aimant est donc fait d’un matériau à caractéristique élevée, par exemple un alliage aluminium – nickel – cobalt et fer ou des poudres frittées comme le ferroxdur : le coût de ces matériaux spéciaux étant en général élevé, on les réserve à la seule partie "M" de l’aimant, les deux branches "N" et "S" étant en acier normal ou fer doux.
Une dernière particularité est donnée par la plaquette métallique "P" qui peut être déplacée à gauche ou à droite (voir Fig. 3) : elle constitue un véritable shunt magnétique et sert à régler, dans les limites naturellement assez restreintes, l’intensité du champ où est plongée la bobine.
Avec un tel système on amène l’aiguille à se placer au fond de l’échelle pour la valeur exacte préétablie, c’est-à-dire qu’on effectue le tarage de l’appareil : ce réglage est fait une fois pour toutes par le constructeur de l’appareil. Comme on l’a vu, la bobine et par conséquent l’aiguille, se déplacent d’un côté ou de l’autre suivant le sens du courant qui la parcourt : ce type d’appareil n’est donc capable que de mesurer des COURANTS CONTINUS, courants qui ont une valeur et un sens constants.
APPAREILS À FER MOBILE
Le principe de construction des appareils à FER MOBILE est donné à la Fig. 4.
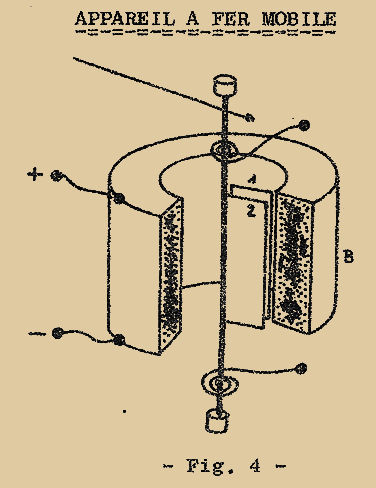
Le système mobile classique formé par l’axe, l’aiguille et les ressorts ne supporte pas le cadre comme dans le type précédent mais seulement une lamelle de fer doux (d’où le nom d’instrument à fer mobile) indiquée "2" sur la Fig. 4.
Près de la lamelle "2" et solidaire de la bobine "B" qui entoure tout le système, se trouve une autre lame "1" également en fer doux, de dimensions analogues à la première.
Quand on fait circuler un courant dans la bobine en branchant les bornes "+" et "-" au circuit intéressé, on crée à l’intérieur de la bobine un champ magnétique qui aimante les lamelles avec une polarité identique à la même extrémité : par exemple avec le pôle positif en haut et le pôle négatif en bas.
Comme les charges magnétiques de même signe se repoussent, des forces naissent qui tendent à éloigner les deux lamelles : la lamelle mobile s’éloignant donc de la lamelle fixe provoque la rotation de l’aiguille.
Comme dans le cas précédent l’aiguille se portera sur une position où le couple moteur (donné par la force de répulsion des deux lamelles) équilibrera le couple antagoniste (celui des ressorts de rappel).
Le déplacement de l’aiguille à partir de sa position de repos sera d’autant plus grand que le champ magnétique sera important, c’est-à-dire que le courant parcourant la bobine sera plus intense.
Pour obtenir un appareil sensible il faut également disposer d’une bobine avec un grand nombre de spires.
Les appareils à fer mobile sont cependant en général, peu sensibles mais, étant donné leur extrême simplicité et leur robustesse, ils sont très utilisés dans l’industrie.
Si on inverse le courant dans la bobine, on inverse aussi le champ magnétique des deux lamelles : celles-ci restent cependant toujours chargées magnétiquement de même signe et de ce fait ont toujours tendance à se repousser. C’est-à-dire qu’en inversant le courant, l’aiguille se déplace encore dans le même sens. Cette propriété rend l’appareil capable de mesurer également des COURANTS ALTERNATIFS.
APPAREIL ÉLECTRODYNAMIQUE
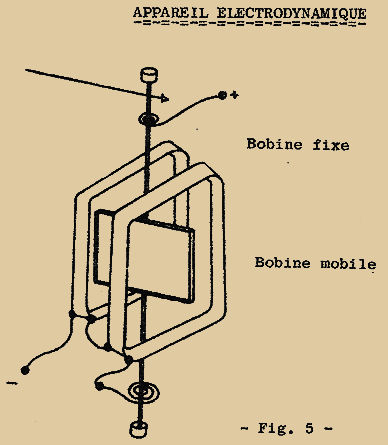
L’appareil électrodynamique fonctionne sur le même principe que l’appareil à bobine mobile, cependant ici le champ magnétique n’est pas obtenu par aimant mais grâce à un enroulement parcouru par le même courant qui traverse la bobine mobile (Fig. 5)
Là aussi, quand on inverse le courant dans la bobine, on inverse également le champ créé par la bobine fixe : l’aiguille se déplaçant toujours dans le même sens, l’appareil est donc capable de mesurer des courants CONTINUS OU ATERNATIFS.
Le déplacement de l’aiguille est proportionnel au CARRÉ de la valeur du courant : c’est pourquoi on a, comme nous l’avons déjà vu, une échelle dite quadratique.
Un quatrième type d’appareil auquel nous ferons allusion et qui a une échelle quadratique comme l’appareil électrodynamique, est l’appareil dit à FIL CHAUD ou APPAREIL THERMIQUE : dans cet appareil on met à profit la dilatation d’un fil due au chauffage provoqué par le passage du courant dans ce même fil (Fig. 6).
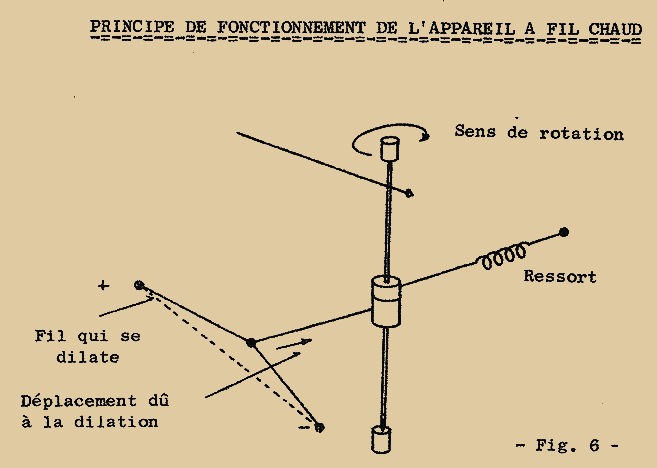
L’allongement du fil, parcouru par le courant à mesurer, provoque la rotation de l’aiguille, rappelée par un ressort à spirale. Comme le chauffage du fil peut-être obtenu, aussi bien par un courant continu que par un courant alternatif, cet appareil peut mesurer à la fois les deux types de courant.
Ajoutons qu’il est délicat et donc d’un emploi peu fréquent.
SENSIBILITÉ ET PRÉCISION D’UN APPAREIL
On confond trop souvent ces deux notions caractéristiques d’un appareil qui sont tout à fait indépendantes l’une de l’autre, ainsi on est porté à croire que plus un instrument est sensible plus il est précis.
Cette croyance est tout à fait arbitraire et vient peut-être de ce que nous allons exposer plus loin. Pour l’instant examinons en détail ce que veulent dire les expressions : SENSIBILITÉ et PRÉCISION.
La sensibilité d’un appareil de lecture est la valeur de la grandeur mesurée par celui-ci correspondant à une GRADUATION de l’échelle.
Supposons qu’on dispose d’un instrument, par exemple un milliampèremètre, dont la valeur en extrémité d’échelle soit de 1 mA et dont l’échelle soit divisée en 50 parties.
Une division de l’échelle correspond alors à un courant de 1/50, soit 0,02 mA = 20 µA, et cette valeur indique la sensibilité de l’instrument considéré : elle exprime la plus petite quantité qui peut être lue sur l’échelle.
Dans le domaine des galvanomètres de laboratoire d’usage commun on prend souvent l’habitude d’exprimer la sensibilité par la valeur d’extrémité d’échelle. Suivant les deux méthodes, plus petite est la valeur correspondant à une graduation, ou plus faible est la valeur en fin d’échelle, plus le galvanomètre sera sensible.
Une méthode universellement adoptée, spécialement pour l’appareil de contrôle (multimètre), consiste à exprimer la sensibilité en "Ω/V". Dans ce cas la sensibilité de l’appareil est d’autant plus élevée que le rapport ohm/volt est plus grand.
La valeur en "Ω/V" est étroitement liée à la valeur d’extrémité d’échelle de l’appareil ; il est donné par la relation suivante :
Par exemple si, pour réaliser un contrôleur, on utilise un galvanomètre avec 1 mA de fin d’échelle, il présentera une sensibilité de 1000/1 = 1000 Ω/V ; si au contraire on utilise un galvanomètre donnant 0,2 mA en fin d’échelle, c’est-à-dire cinq fois plus sensible, on aura une sensibilité finale de 1000/0,2 = 5000 Ω/V.
L’expression "Ω/V" (ohm par volt) est justifiée par le fait que cette valeur indique aussi la résistance présentée par l’appareil utilisé comme voltmètre avec 1 Volt en fin d’échelle.
En effet dans le cas d’un instrument à 5000 Ω/V, si on veut que celui-ci aille en bout d’échelle pour 1V, il faudra qu’en appliquant cette tension à ses bornes, il soit parcouru par un courant de 0,2 mA (0,0002 A) ; d’après la loi d’Ohm il devra donc présenter une résistance de 1/0,0002 : soit 5000 ohms.
La notion de PRÉCISION est au contraire liée à l’aptitude qu’a l’appareil d’indiquer plus ou moins exactement la valeur des grandeurs mesurées, c’est-à-dire qu’elle est LIÉE à L’ERREUR PROBABLE que l’on peut faire en effectuant une mesure INDÉPENDAMMENT DE LA SENSIBILITÉ PROPRE.
La précision d’un instrument dépend du soin avec lequel il a été construit et réglé, et NON DE LA VALEUR d’extrémité d’échelle.
Selon les normes U.T.E. (Union Technique de l’Électricité) on exprime la précision d’un instrument par l’erreur maximum garantie par le constructeur.
En général cette erreur est donnée en pourcentage par rapport à la valeur d’extrémité d’échelle ; les classes de précision normalisées sont : 0,1 – 0,2 – 0,5 – 1 – 1,5 – et 2,5. La valeur d’extrémité d’échelle s’appelle souvent le CALIBRE du galvanomètre.
Supposons qu’on dispose d’un appareil qui soit, pour fixer les idées, un voltmètre avec 100V en bout d’échelle et qu’il soit garanti avec une précision de 1%.
Ceci signifie alors que lorsque cet instrument indique 100V, la mesure peut être affectée d’une erreur de 1V : la valeur vraie de la tension mesurée n’est pas exactement 100 Volts mais est comprise entre 99V et 101V. Il faut remarquer ici que la précision est rapportée à la VALEUR D’EXTRÉMITÉ D’ÉCHELLE ET NON À LA VALEUR QUE L’ON LIT SUR L’ÉCHELLE.
Expliquons-nous plus clairement : si avec ce voltmètre on mesure une tension de 50V, c’est-à-dire si l’aiguille est à mi-échelle, l’erreur n’est pas maintenant de 0,5V (1% de 50V) mais RESTE ENCORE de 1V (1% de 100V).
On ne pourra donc dire que la valeur vraie est comprise entre 49,5V et 50,5V mais qu’elle est comprise entre 49V et 51V. Si la mesure ne porte que sur 10 V, la valeur vraie sera comprise entre 9V et 11V, et non entre 9,9V et 10,1V, ce que l’on pourrait croire en appliquant la marge de 1% à 10V (valeur lue) au lieu de la rapporter à la valeur d’extrémité d’échelle.
En définitive, avec cet appareil toute la valeur indiquée peut différer de la vraie valeur d’au plus 1V (en plus ou en moins. Cette erreur maximum de 1V est dans ce cas-là seulement, imputable au galvanomètre.
L’erreur effective pourra être encore plus grande si l’appareil n’est pas correctement utilisé, s’il n’est pas adapté à la mesure que l’on veut effectuer, ou s’il comporte des éléments dont les erreurs propres viendront s’ajouter.
Un cas typique d’erreur que l’on commet avec les voltmètres est dû au fait que l’appareil absorbe un certain courant et donc que le circuit peut être perturbé par modification des tensions à mesurer.
Voici un exemple simple : on dispose d’un diviseur de tension formé par deux résistances et on désire mesurer la tension "V2" entre les points "C" et "D" quand on applique entre "A" et "B" une tension "V1 = 200V" (Fig. 1).
DIVISEUR DE TENSION ET BRANCHEMENT DU VOLTMÈTRE
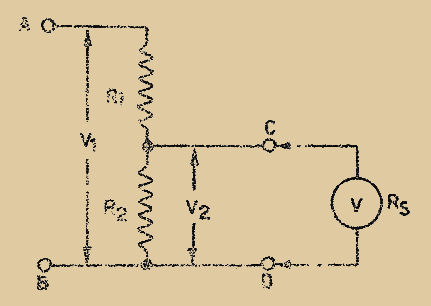
Fig. 1
Si les résistances ont la valeur indiquée sur la Fig. 2, c’est-à-dire 100kΩ chacune, il est évident que la tension "V2" sera moitié de "V1" (dans l’exemple "V2 = 100V").
Il n’en va pas de même lorsque, entre "C" et "D" on branche l’instrument de mesure.
CIRCUIT ÉQUIVALENT DU DIVISEUR ET DU VOLTMÈTRE DE 100 Ω/V
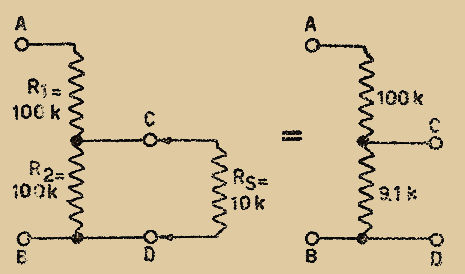
Fig. 2
Maintenant, en parallèle entre "C" et "D", on trouve la résistance "Rs" de l’appareil et plus celle-ci sera petite vis-à-vis de "R2", plus la tension "Vs" mesurée sera faible vis-à-vis de celle qui existait lorsque l’appareil n’était pas connecté, c’est-à-dire "V2".
Voyons en effet ce qui arrive quand on fait cette mesure avec des appareils ayant différentes sensibilités, c’est-à-dire avec des voltmètres de 100V présentant des sensibilités de 100 Ω/V, 500 Ω/V et 100.000 Ω/V.
Dans le premier cas donné à la Fig. 2, la résistance "Rs" de l’appareil est de :
"RS" et "R2" se trouvant en parallèle, on peut faire un schéma équivalent où :
La tension "V2" entre "C" et "D" se réduira alors à la valeur :
Et l’erreur commise est alors de 84 %.
Dans le second cas (Fig. 3) on a au contraire RS = 5000 x 100 = 500.000 = 500 kΩ.
CIRCUIT ÉQUIVALENT DU DIVISEUR ET VOLTMÈTRE de 5.000 Ω/V
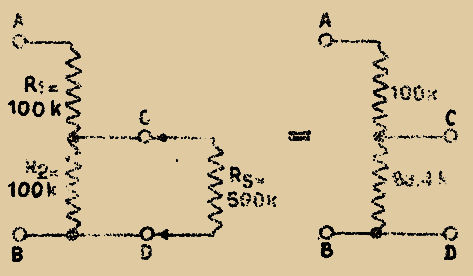
Fig. 3
Enfin dans le troisième cas (Fig. 4) Rs = 100.000 x 100 = 10.000.000 Ω = 10 MΩ
CIRCUIT ÉQUIVALENT DU DIVISEUR ET VOLTMÈTRE DE 100.000 Ω/V
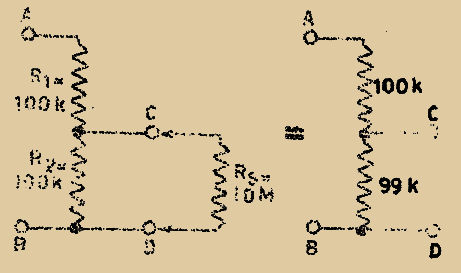
Fig. 4
Dans ces trois exemples, apparaît clairement l’influence de la consommation de l’appareil sur le résultat de la mesure.
Celle-ci est d’autant plus gênante, que la résistance du circuit est négligeable par rapport à la résistance interne de l’appareil ; en d’autres termes, il est nécessaire pour avoir des erreurs négligeables que le courant absorbé par l’appareil soit négligeable par rapport à celui qui parcourt le circuit.
Dans les circuits radio, il existe des courants très faibles, dans certains cas quelques dixièmes de mA ; il faut donc avoir des galvanomètres suffisamment sensibles, c’est-à-dire avec un faible courant pour une déviation complète de l’aiguille.
Les multimètres sérieux sont des appareils de 5.000 à 10.000 Ω/V dont la valeur de fin d’échelle est aux environs de 0,2 à 0,1 mA. Ils fonctionnent bien tant qu’ils sont utilisés dans des circuits traversés par quelques mA et sont donc capables de mesurer des tensions dans les circuits classiques de cathode de plaque ou de grille écran, où les courants sont de cet ordre de grandeur.
Dans ces mesures l’erreur est limitée à quelques pourcentages (voir l’exemple de la Fig. 3).
L’erreur commise dans la mesure des circuits de grille de commande est par contre intolérable, de même que dans les circuits de commande automatique de sensibilité.
Heureusement les VOLTMÈTRES ÉLECTRONIQUES viennent ici à notre aide car le courant qu’ils absorbent est extrêmement faible comme on le verra ultérieurement (3ème Partie de ce Cours).
La SENSIBILITÉ du galvanomètre peut donc avoir une très grande importance sur la PRÉCISION DE MESURE, selon le circuit dans lequel on effectue la mesure.
Il ne faut pas pour autant confondre sensibilité et précision d’un appareil qui sont comme on l’a vu deux choses bien distinctes.
L’erreur due à la consommation de l’appareil, donc à sa sensibilité, n’altère en rien sa précision, bien qu’elle puisse altérer la précision de la mesure : car il s’agit là d’une erreur SYSTÉMATIQUE, que l’on peut ramener à une valeur acceptable en utilisant des instruments adaptés au circuit où doit s’effectuer la mesure ; elle peut être calculée avec précision comme on l’a dans les exemples précédents, et l’on pourra opérer la CORRECTION nécessaire.
Pour faire une bonne mesure il ne suffit donc pas d’utiliser des instruments suffisamment sensibles, mais il est absolument nécessaire qu’ils soient d’une précision adaptée aux exigences de la mesure.
NORMES "U.T.E." ET SYMBOLES GRAPHIQUES
Les appareils de mesure sont divisés en cinq catégories suivant la classe de leur précision, à savoir :
Ces chiffres représentent la valeur maximum de l’erreur due au galvanomètre lui-même.
L’erreur maximum admissible en un point quelconque de l’échelle ne doit donc pas être supérieure aux limites suivantes.

Les appareils de mesures répondent à des normes de construction et de présentation établies par l’UNION TECHNIQUE DE L’ÉLECTRICITÉ, en abrégé "U.T.E." (54, Avenue Marceau à Paris) : c’est l’U.T.E. qui définit les classes d’appareils, ainsi que les symboles qu’ils doivent respecter.
Les appareils étalons sont des appareils de classe 0,1, 0,2 ou à la rigueur 0,5 : ils servent presqu’exclusivement à contrôler les autres appareils.
Aux classes 1 et 1,5 appartiennent les appareils servant aux mesures de précision, tandis que les appareils d’usage courant relèvent de la classe 2,5 ou n’appartiennent encore à aucune de ces catégories, quand leur précision est moins bonne et que leurs erreurs sont supérieures à la limite de 2,5%.
Outre la classe de l’appareil qui indique sa précision, on aura également avantage à distinguer le TYPE de l’appareil, le CIRCUIT pour lequel il est prévu, la POSITION dans laquelle il doit être placé ainsi que la TENSION MAXIMUM d’isolement qu’il peut supporter à ses bornes.
Pour pouvoir commodément marquer ces indications sur l’instrument, on a convenu d’établir des symboles d’écriture qui sont gravés sur le cadran de l’appareil.
Ces symboles sont couramment utilisés en Europe, alors qu’ils n’existent généralement pas sur les instruments américains et c’est là une grave lacune car pour bien utiliser un appareil et interpréter correctement ses indications, il faut connaître ses caractéristiques.
Dans les Tableaux suivants on a rassemblé les symboles conventionnels normalisés par l’U.T.E. Outre ceux-ci, il peut être marqué sur l’appareil la classe à laquelle il appartient, et s’il est valable en courant alternatif, la plage de fréquences dans laquelle on peut l’utiliser.
Lorsque cette dernière indication fait défaut, cela veut en général dire que l’appareil est correct entre 15 et 60 Hz.






LA TECHNOLOGIE DES PIÈCES DÉTACHÉES
Toute pièce détachée utilisée dans un circuit radio doit être choisie pour amener un fonctionnement correct ; en dehors du choix qui préside à la SÉLECTION de telle pièce adaptée ou non au mode de fonctionnement propre du circuit, il faut encore que la pièce réponde aux EXIGENCES EXTÉRIEURES du circuit électronique.
Expliquons-nous par un exemple : supposons qu’il s’agisse de placer une résistance d’amortissement entre les extrémités d’un circuit accordé ; bien entendu nous aurons calculé sa valeur, choisi la précision pour respecter la fréquence d’accord cherchée, et fixé le type de wattage qui convient au courant de circulation. Nous aurons en somme défini les caractéristiques premières de la résistance, à savoir :
- Valeur
- Précision
- Wattage
Mais supposons maintenant que ce circuit d’accord soit prévu pour fonctionner à une température ambiante de 80° C : nous avons alors obligation de tenir compte de cette nouvelle condition, puisque les caractéristiques de la résistance ont été antérieurement choisies pour une ambiante normale (20° C généralement). La précision peut ainsi varier et le wattage ne pas être suffisant.
Admettons maintenant que le circuit soit accordé sur 1 MHz : on sait que les résistances d’amortissement sont traversées par des courants à très haute fréquence, et l’expérience montre que la "valeur ohmique" peut être une fonction de la fréquence, ainsi une résistance qui mesure 1 MΩ en courant continu ne conserve plus du tout la même valeur à 1 MHz.
De plus, et ceci est très grave, tout se passe comme si une capacité de plus en plus grande se présentait entre les deux extrémités des circuits d’accord à mesure qu’augmente la fréquence ; la présence de cette capacité parasite peut dérégler les circuits.
On voit ainsi comment une pièce détachée, régulièrement choisie pour un circuit théorique donné, peut en fait n’être absolument pas adaptée à son fonctionnement par suite de conditions d’"ambiance" totalement étrangère aux règles de sélection naturelle de la pièce en question.
L’ensemble des conditions extérieures propres au fonctionnement d’une pièce se nomment les CONDITIONS TECHNOLOGIQUES et les CONDITIONS CLIMATIQUES : ainsi les pièces détachées de tout équipement militaire doivent répondre à des NORMES ou SPÉCIFICATIONS TECHNOLOGIQUES d'autant plus sévères que le travail des pièces est sévère.
C’est l’Union Technique de l’ÉLECTRICITÉ (U.T.E.) et l’Association Française de Normalisation ("AFNOR") qui ont établi les normes concernant les matériels utilisés dans les télécommunications par fil et par radio ; ces spécifications techniques sont classées en trois catégories :
- Les spécifications générales concernant les propriétés et le comportement des pièces détachées du matériel de transmission, ainsi que les essais généraux relatifs à ces pièces
- Les spécifications de groupe relatives aux qualités à exiger des pièces détachées appartenant à un groupe donné : par exemple les condensateurs.
- Les spécifications particulières relatives à chaque type de pièces détachées : par exemple les condensateurs au papier.
On notera l’importance de plus en plus grande prise par la technologie dans la construction électronique : les performances toujours accrues des pièces détachées sont accompagnées des garanties toujours plus complètes sur la "Sécurité de Fonctionnement" de la pièce.
Pour ce qui est de l’endurance de la pièce aux conditions extérieures, citons les facteurs d’influence les plus courants :
La température, tant en valeur absolue – température ambiante – qu’en variations brutales
L’humidité, ou "degré hygrométrique", qui jointe à la température élevée cause souvent des dégâts considérables dans les équipements.
La corrosion, en particulier sur certaines pièces soumises à l’air salin.
La contrainte mécanique, chocs, secousses ou vibrations.
La tension d’isolement
La température maximale généralement désignée par température critique ou température limite de fonctionnement
Nous ajouterons la fréquence de fonctionnement que nous avons déjà mentionnée plus haut.
On voit donc l’importance qu’il y a à définir dans son cadre réel de travail, puis à choisir parmi celles les mieux adaptées, la pièce qui conviendra à un circuit donné, mais on ne peut raisonnablement parler de mesures si les circuits ne sont pas convenablement raccordés entre eux, et si l’on n’a pas pris les précautions élémentaires de blindage lorsque le domaine des fréquences de travail l’exige : ceci nous amène tout naturellement à traiter les deux sujets de base : les CONNEXIONS et les ÉCRANS.
LES CONNEXIONS
Elles peuvent être de trois types : connexions en COURANT CONTINU, en COURANT ALTERNATIF, connexions de MASSE.
1 – Connexions en courant continu :
Les connexions doivent avoir une RÉSISTANCE FAIBLE devant les résistances utiles du montage afin de ne provoquer que des chutes de tension négligeables. En outre leur section doit être suffisante pour que la densité de courant qu’elles admettent n’entraîne un échauffement par effet Joule.
Lorsque les connexions s’effectuent par serrage de bornes, il faudra que les bornes et les fils aient une surface bien décapée : des contacts incertains déterminent des résistances essentiellement variables.
Dans le cas où les appareils de mesures utilisés sont sensibles aux courants alternatifs, il faut éviter que les circuits ne soient le siège de COURANTS INDUITS : on y parvient en veillant à ce que le circuit NE FORME PAS UNE BOUCLE enfermant une grande surface.
Enfin lors des mesures de précision, on placera l’ensemble du circuit dans une température ambiante uniforme pour éviter des EFFETS THERMO-ÉLECTRIQUES au contact de deux métaux de nature différente.
2 – Connexions en courant alternatif :
En courant alternatif, les connexions devront tenir compte des éléments suivants :
- Capacité parasite entre fils
- Rayonnement des conducteurs
- Inductions diverses.
Aux fréquences basses, inférieures à 200 kHz, on sera amené à utiliser pour les liaisons des paires de câbles symétriques.
Aux fréquences supérieures à 200 kHz, on utilisera de préférence la PAIRE COAXIALE.
En outre, quel que soit le type de paire utilisée, dans le cas surtout où les liaisons sont longues, on les raccordera sur l’IMPÉDANCE CARACTÉRISTIQUE de la paire pour améliorer le transfert de puissance.
L’impédance d’une paire symétrique est comprise entre 150 et 800 Ω environ ; celle d’une paire coaxiale entre 50 et 100 Ω environ.
3 – Connexions de masse
Les connections de masse ont pour but de FIXER LE POTENTIEL d’un montage par rapport au sol. Ceci évite que pour des causes quelconques ce potentiel ne puisse prendre des valeurs dangereuses pour l’opérateur ou n’engendre des perturbations gênantes.
Une connexion de masse est donc représentée par un conducteur relié à une prise de terre : pour qu’elle soit efficace, il faut qu’elle ne soit le siège que de courants négligeables ; la prise de masse ne doit jamais servir de conducteur de retour à un courant. En alternatif, on veillera à ce que les connexions à la prise de la masse ne forment pas de boucle pour qu’elles ne deviennent pas le siège de courants induits.
LES ÉCRANS
Les écrans se classent en deux catégories :
- Les écrans électrostatiques.
- Les écrans magnétiques.
Leur but est de soustraire les éléments qu’ils renferment à l’influence de champs continus électrostatiques et magnétiques.
1- Les écrans électrostatiques
Une bonne illustration de l’écran électrostatique est celle de la CAGE DE FARADAY.
Une autre application est celle des BOBINAGES : dans un bobinage en fil rangé, les premières couches voisines du circuit magnétique relié à la masse présentent par rapport à la masse une capacité plus élevée que les dernières spires.
On égalisera ces capacités en disposant des écrans reliés à la masse au début et à la fin du bobinage. Entre les deux enroulements d’un bobinage de transformateur on placera un écran à la masse qui SUPRIMERA LES CAPACITÉS ENTRE ENROULEMENTS. Les écrans de bobinage sont généralement constitués par une feuille de clinquant de 0,01 mm environ.
2- Les écrans magnétiques
Les écrans magnétiques sont destinés à protéger les éléments qu’ils renferment des influences du FLUX D'INDUCTION EXTÉRIEUR. Plus leur perméabilité propre est élevée, et donc moins ils sont saturés par le flux qui les parcourt, plus la protection qu’ils offrent est efficace.
Une illustration courante des écrans magnétiques est le blindage des TUBES CATHODIQUES à déviation électrostatique : les champs magnétiques parasites dus principalement au transformateur d’alimentation ont pour effet de défocaliser le faisceau, et donc de le dévier, ce que l’on évite par un écran en NUMETAL entourant le col du tube cathodique.
LES PIÈCES DÉTACHÉES
On a vu l’importance que présentaient les performances des PIÈCES DÉTACHÉES dans toute mesure : il ne faut pas seulement pour qu’une mesure soit bonne appliquer une bonne méthode et se servir d’un appareil précis et sensible, il faut aussi utiliser de bonnes pièces détachées.
Les pièces détachées dont dispose l’électronique moderne comprennent des ÉLÉMENTS PASSIFS dont le fonctionnement ne nécessite pas la présence de source d’énergie auxiliaire, et des ÉLÉMENTS ACTIFS dont le fonctionnement exige la présence de telles sources.
Les éléments passifs se divisent en deux classes : les éléments LINÉAIRES et les éléments NON LINÉAIRES, les premiers obéissent à la loi de proportionnalité.
Les éléments actifs sont NON LINÉAIRES par définition :
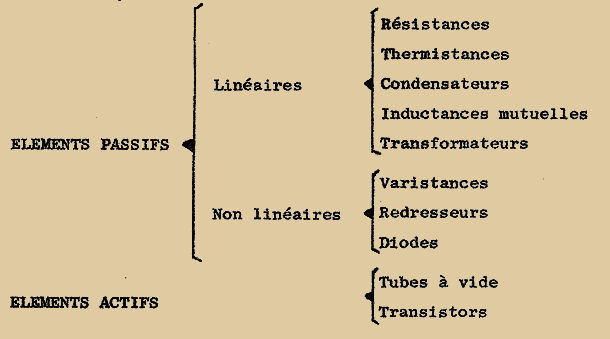
Les caractéristiques des différentes pièces détachées seront passées rapidement en revue dans les prochaines leçons.
LES PIÈCES DÉTACHÉES DANS LES MESURES
LES RÉSISTANCES
Paramètres
Une résistance est caractérisée par sa valeur nominale à la température ordinaire, cette valeur dépend de la RÉSISTIVITÉ du corps qui la constitue et de ses dimensions géométriques :
où :
- R est la résistance
- ρ est la résistivité du corps (matériau considéré)
- l est la longueur du corps
- s est la section du corps
La résistivité dépend de la température suivant la loi :
α est le coefficient de température propre au corps considéré.
Le coefficient α peut se définir de la façon suivante :
La résistance dépend également de la FRÉQUENCE. L’effet d’une augmentation de fréquence est double : d’une part la résistance est augmentée par le fait que les courants à haute fréquence se réfugient sur la surface des conducteurs. C’est l’EFFET DE PEAU ; d’autre part la répartition des filets de courant dans la résistance lui donne une INDUCTANCE PROPRE et une CAPACITÉ, de telle sorte que le schéma équivalent d’une résistance en "H.F." est celui de la Fig. 1, où l’on voit une résistance PURE "r" en série avec une inductance "ℓ" et un condensateur "c" en parallèle.
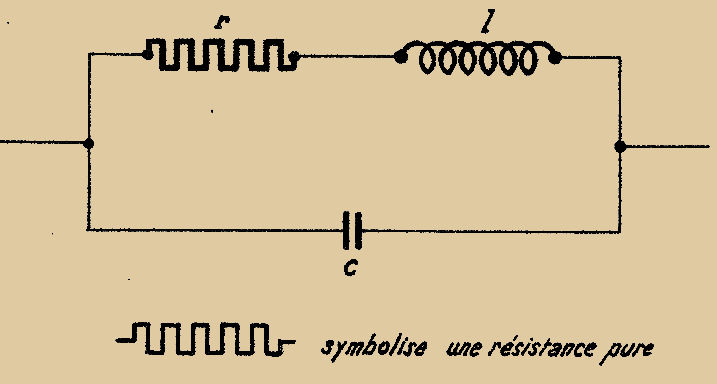
Fig. 1
La résistance dépend aussi de l’intensité qui la parcourt par l’action combinée de l’effet Joule qui en provoque l’échauffement et de son coefficient de température qui la fait varier : en effet on a vu plus haut que la résistivité variait avec la température.
En outre, on devra connaître pour son utilisation la puissance maximum que la résistance peut dissiper sans risque de destruction.
Résistances Bobinées
Le Tableau suivant donne les valeurs de la résistivité et du coefficient de la température de quelques métaux ou alliages utilisés dans la construction des RÉSISTANCES À FIL :
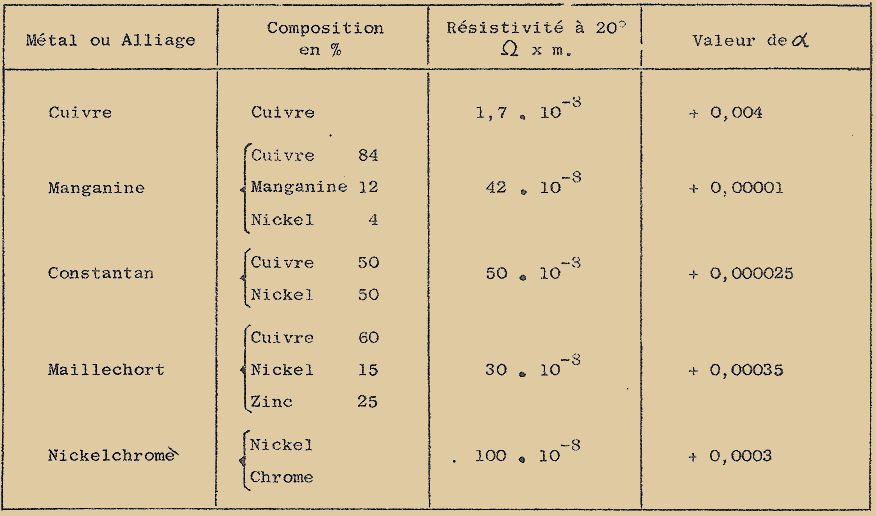
Nous observons que le Manganine est le matériau capable de réaliser des résistances les plus constantes avec la température, cependant que le Nickel-chrome permet la réalisation des fils les plus résistants ; le cuivre par contre est le matériau le moins résistant, mais sa variation avec la température n’est pas négligeable.
Il va sans dire qu’une résistance bobinée peut avoir un coefficient de température propre assez différent de celui α de la résistivité du matériau utilisé.
Une résistance bobinée dépend de la fréquence par suite de :
- L’effet de peau
- La présence d’une inductance propre et d’une capacité répartie.
a- L’ÉFFET DE PEAU (en anglais : "skin effect") a pour résultat de chasser le champ électromagnétique à la périphérie des conducteurs ; ainsi la résistance d’un fil de cuivre de 0,1 mm de diamètre augmentera à une fréquence de 1 MHz d’environ 2% par rapport à la résistance en courant continu.
Plus le fil sera d’un matériau à résistivité élevée, moins l’effet de peau sera sensible.
Pour lutter contre l’effet de peau, on emploie du fil divisé à brins isolés les uns des autres : le FIL DE LITZ.
b- L’INDUCTANCE propre est due aux flux embrassés par le bobinage ; on la réduit en diminuant l’induction, c’est-à-dire en réalisant des enroulements unifilaires à sens alternativement inversés, ou bien en bobinant avec deux fils en main.
c- LA CAPACITÉ RÉPARTIE est due au voisinage des spires du bobinage : on la diminue en réduisant les voisinages au maximum.
Une résistance bobinée conserve toujours de l’inductance et de la capacité répartie ; si toutefois celles-ci sont faibles, c’est-à-dire si :
et rcω est beaucoup plus petit que 1
On peut réaliser dans une large plage de fréquences une compensation, comme par exemple dans les résistances haute fréquence de précision : en ce qui concerne ces dernières, le support sur lequel on bobinera le fil devra évidemment être à l’abri des pertes "H.F." par une imprégnation convenable.
Résistances agglomérées et à couche :
Les résistances du premier type sont constituées par de la poudre de carbone agglomérée par un mélange résineux. Ce sont des fabrications économiques, mais elles présentent de graves inconvénients : instabilité, variation importante avec la température, sensibilisation à l’humidité.
Les résistances à couche sont réalisées à partir d’un dépôt de métal ou de carbone, sur un mandrin de stéatite ou de céramique, que l’on émaille au four pour fixer la couche conductrice.
De telles résistances sont peu sensibles à l’effet de peau et ont une capacité répartie négligeable.
Résistances variables :
Les résistances variables comprennent deux groupes :
- Les résistances variables de façon discontinue, par exemple la boîte de résistances à décades.
- Les résistances variables de façon continue, comme le potentiomètre.
a– RÉSISTANCES VARIABLES DE FAÇON DISCONTINUE :
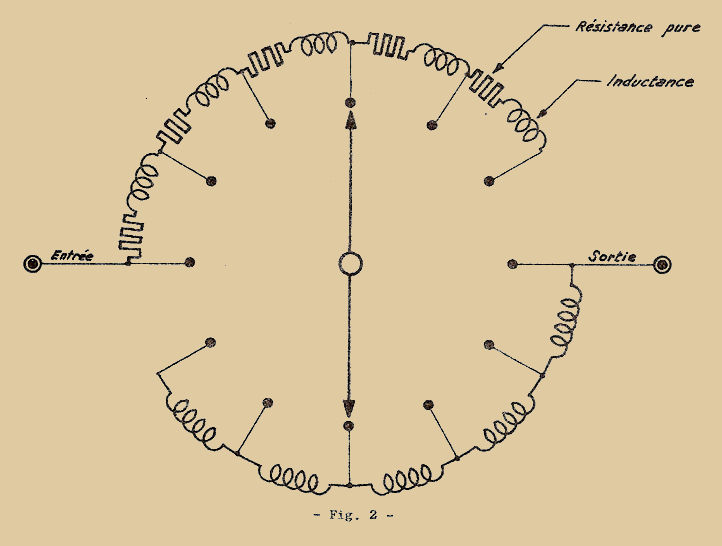
Fig. 2
Il s’agit souvent de résistances bobinées variables à commutateurs, ainsi la Fig. 2 qui montre un type de résistance variable à INDUCTANCE CONSTANTE utilisée dans un pont de mesure "H.F.".
Les principales difficultés de fabrication se trouvent dans les commutateurs qui doivent présenter de très faibles résistances de contact, aussi faibles que possible.
Il faut assurer de bons contacts entre plots et balai du commutateur, tout en assurant de faibles capacités entre plots et par rapport à la masse.
b– RÉSISTANCES VARIABLES DE FAÇON CONTINUE :
Ces résistances variables sont construites sous forme de résistances à collier, de rhéostats potentiomètriques, de potentiomètres bobinés et au carbone
Les résistances à collier sont des résistances bobinées vitrifiées munies d’un ou plusieurs colliers de serrage entrant en contact avec une face dénudée du bobinage
Les rhéostats potentiomètriques sont le plus souvent utilisés pour le réglage de fortes intensités.
Les potentiomètres bobinés restent valables jusqu’à des fréquences de 20 kHz, pourvu que leur dissipation ne soit pas excessive.
Les potentiomètres au carbone, où le bobinage est remplacé par une couche de carbone agglomérée, peuvent être utilisés jusqu’à des fréquences de 500 kHz : la résistance de contact devra être limitée au minimum, ce qui évitera en outre tout échauffement qui modifierait la résistance globale.
LES THERMISTANCES
Les Thermistances sont des résistances à FORT COEFFICIENT NÉGATIF DE TEMPÉRATURE que l’on utilise pour la mesure ou la COMPENSATION des températures, ou bien comme éléments RETARDATEURS dans les circuits à relais.
Ainsi pour éviter qu’un circuit avec résistances à couche de bonne précision plongé dans une température élevée ne subisse des variations trop importantes, on compense les résistances classiques par des thermistances qui varient en sens inverse des premières.
Les Thermistances sont constituées de SEMI-CONDUCTEURS composés de matériaux isolants et d’oxydes métalliques ; leur conductibilité (c’est-à-dire l’inverse de la résistivité) est donnée par la relation :
où :
- A et "a" sont des constantes caractéristiques du semi-conducteur
- e est la base du logarithme népérien = 2,718
- T est la Température absolue en degrés Kelvin = t° C + 273
- Le coefficient de température α est donné par :
Il est négatif et décroit quand la température augmente ; pour les températures ordinaires 27° C (soit T = 300° Kelvin), le coefficient de température est de l’ordre de -4.10-2, alors que nous avons vu plus haut que le coefficient de température des résistances était de l’ordre de +4.10-3 La Thermistance a une valeur résistive qui dépend de la fréquence, et présente une inductance qui atteint un maximum pour une fréquence critique de fonctionnement propre au matériau.
Les Thermistances sont plus ou moins stables dans le temps d’après leur type de construction et le traitement qui a été appliqué.
LES PIÈCES DÉTACHÉES DANS LES MESURES (suite)
LES CONDENSATEURS
Paramètres :
Un condensateur est caractérisé par sa capacité nominale à la température ordinaire qui dépend de la superficie des armatures, de l’épaisseur du diélectrique qui les sépare et du pouvoir inducteur de ce diélectrique.
La capacité d’un condensateur plan est donné par la formule :
où :
- ε est le pouvoir inducteur spécifique
- S est la superficie des armatures
- e est l’épaisseur du diélectrique
La capacité est fonction de la température, le coefficient de température entre les températures "t" et "t’" se définit par :
α peut être positif ou négatif suivant les matériaux utilisés.
Un condensateur est également caractérisé par sa RÉSISTANCE DE FUITE et sa TENSION DE SERVICE ; la première correspond à une conductibilité qui n’est pas tout à fait nulle : un condensateur chargé finit par se décharger lentement.
La tension de service est la tension maximum à laquelle on pourra soumettre le condensateur sans risque de CLAQUAGE, ce qui aurait pour effet immédiat de détruire le condensateur.
En alternatif, des PERTES prennent naissance dans le matériau diélectrique, comme on le verra plus loin avec les matériaux magnétiques.
Ces pertes peuvent se représenter par une capacité "C1" en série avec une résistance "R1" (Fig. 1) ou par une capacité "C2" en parallèle avec une résistance "R2" (Fig. 2). Les Fig. 1 et 2 ne tiennent pas compte de la résistance de fuite.
L’ANGLE COURANT-TENSION, au lieu d’être rigoureusement égal à π/2 est égal à :
δ (delta) est appelé ANGLE DE PERTE, et est donné par : tangente δ = R1.Cω = 1/(R2.Cω)
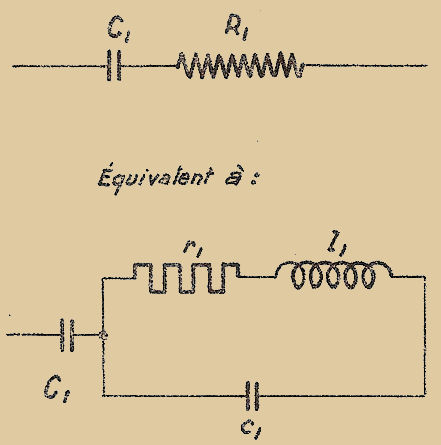
Fig. 1
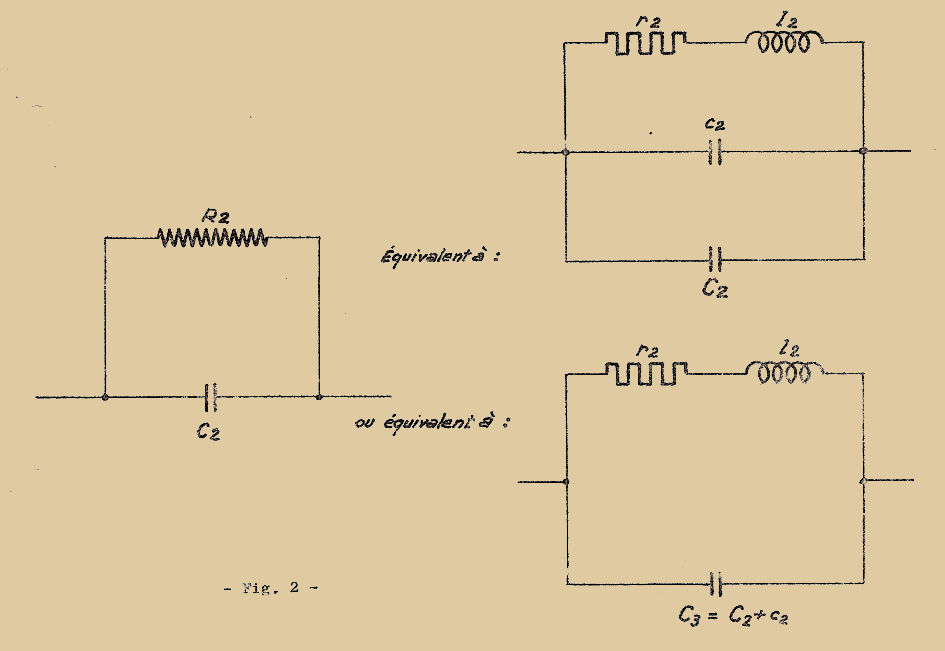
L’angle de perte des condensateurs dépend un peu de la fréquence. On appelle l’inverse de l’angle de perte : LE COEFFICIENT DE QUALITÉ du condensateur. Si l’on applique une tension "U" aux bornes du condensateur, il circule un courant efficace "I", et la puissance dissipée dans le diélectrique du condensateur est donnée par :
Cette puissance dissipée a une LIMITE SUPÉRIEURE au-dessus de laquelle la durée de vie du condensateur est LIMITÉE.
Le tableau suivant indique les grandeurs de l’angle de perte et de la tension de service pour les modèles les plus courants :

Condensateurs Fixes :
Les condensateurs ÉLECTROCHIMIQUES (électrolytiques) qui sont parmi les moins chers du marché à capacité et tension de service ne fonctionnent que POLARISÉS avec un courant de fuite non négligeable, leur capacité dépendant de la polarité.
Ils perdent leurs qualité au-dessous de 0°C, et au-dessus de 50°C ce qui les rend impropres à toutes mesure précise où l’ambiante n’est pas rigoureusement constante.
Condensateurs Bobinés :
Il s’agit là de condensateurs réalisés par bobinage simultané sur les armatures de ruban métallique et de ruban de diélectrique qui le plus généralement est du papier.
Bien qu’imprégné à chaud sous pression, le papier a presque toujours une teneur en humidité non négligeable qui réduit la robustesse du condensateur à la tension de service.
Le remplacement du papier par du styroflex qui est un matériau thermoplastique réduit considérablement les pertes ; les condensateurs au styroflex ont un coefficient de température négatif.
Condensateurs Empilés :
Les condensateurs empilés sont constitués par la mise en parallèle d’un certain nombre de condensateurs plans (Fig. 3)
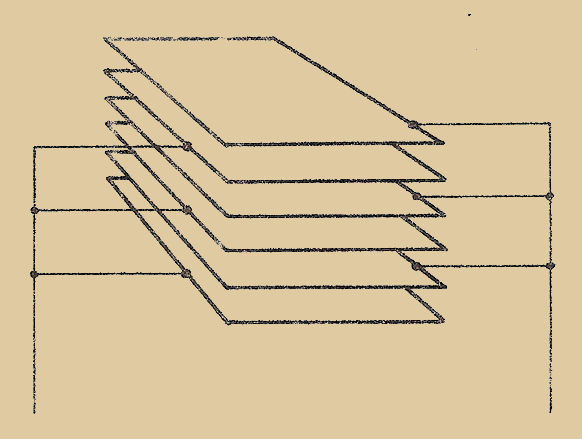
Fig. 3
De tels condensateurs présentent une inductance propre assez faible puisque celle-ci est surtout due aux connexions
Les condensateurs au mica les plus employés ont l’avantage d’offrir une valeur élevée de la constante diélectrique et une tension de claquage importante. Leur coefficient de température est faiblement positif.
Condensateurs Céramique :
L’emploi de ces condensateurs est très répandu dans la technique des fréquences élevées au-delà de 10MHz.
Les céramiques peuvent être, soit des céramiques à constante diélectrique moyenne présentant des angles de perte très faibles, soit des céramiques à forte constante diélectrique ayant des angles de pertes encore acceptables.
Par leur grande rigidité diélectrique, ils sont très utilisés dans les circuits de mesure.
Condensateurs Variables :
Les condensateurs variables et ajustables sont caractérisés par leur capacité maximum admissible et leur capacité résiduelle, cette dernière atteignant en général le dixième de la première.
Les condensateurs variables sont le plus souvent des condensateurs à AIR dont le stator est isolé de la masse, et le rotor mis à la masse par l’intermédiaire de contact circulaire et d’un frotteur.
L’isolement doit être réalisé avec des matériaux fortement isolants (stéatite) surtout s’il s’agit de condensateurs de précision fonctionnant à fréquence élevée (Fig. 4). La liaison du rotor doit bien entendu être de résistance négligeable (bonne pression de contact), et d’inductance faible.
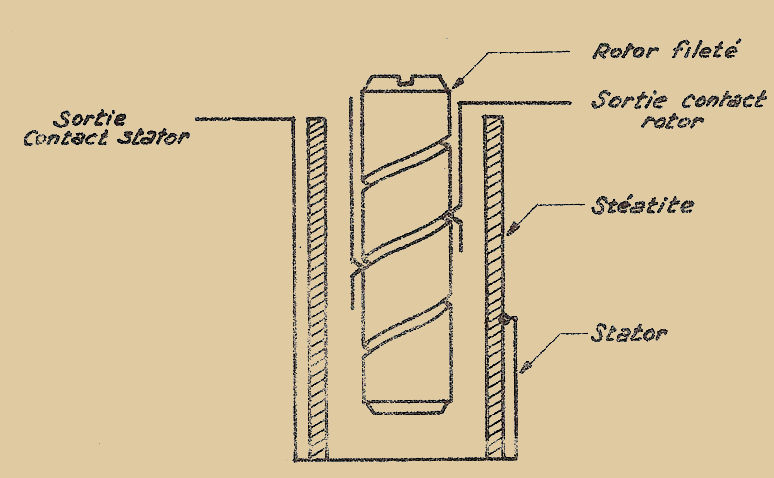
Fig. 4
Dans les condensateurs variables de précision, la tangente δ est inférieure à 10-4.
La capacité varie en fonction de l’angle de rotation du rotor, ce que l’on obtient par un excentrement convenable de l’axe des armatures mobiles : on obtient par exemple des condensateurs dont la capacité varie linéairement en fonction de la fréquence ou de la longueur d’onde, ce qui est le cas des condensateurs d’accord de récepteurs.
LES PIÈCES DÉTACHÉES DANS LES MESURES (suite)
LES INDUCTANCES
Paramètres des inductances à air :
On sait que pour une inductance à bobine droite sur air, sa valeur est donnée par la relation :
où :
- µ0 est la perméabilité de l’air
- n le nombre de spires
- S la section moyenne de la spire
- ℓ l’épaisseur de la bobine
On admet que le flux se referme à travers tout l’espace environnant dont la reluctance est négligeable.
Une inductance propre sur air est en outre caractérisée par :
- La résistance de son bobinage "R"
- La capacité répartie "C" de ce bobinage qui, s’il s’agit de fréquences pas trop élevées, équivaut à une capacité en parallèle sur la bobine.
Ainsi une inductance sur air équivaut au circuit de la Fig. 1.
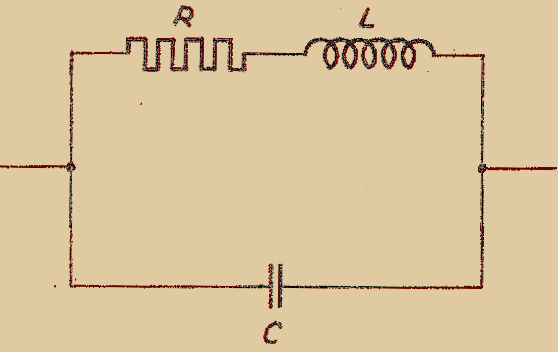
Fig. 1
La caractéristique première d’une inductance sur air est sa faible valeur, ce qui limite son utilisation aux fréquences élevées : pratiquement la bande d’utilisation couvre de 1MHz à quelques centaines de MHz.
Aux fréquences les plus basses, les bobinages utilisés sont du type à NID D’ABEILLES ; aux fréquences plus élevées on emploie des bobinages en fil rangé.
Les inductances variables servent souvent à réaliser des MUTUELLES VARIABLES.
Rappelons la définition du COEFFICIENT D’INDUCTANCE MUTUELLE :
On sait qu’une bobine d’inductance est constituée par un bobinage qui embrasse un flux d’induction magnétique ɸ circulant dans un système de plusieurs milieux formant le circuit de la bobine. Ce flux est créé par le courant continu "I" circulant dans la bobine, il est proportionnel au courant "I" et on définit le coefficient d’inductance propre de la bobine par la relation :
Deux bobines d’inductance sont dites COUPLÉES PAR INDUCTANCE MUTUELLE lorsque la bobine N°1 embrasse un flux d’induction magnétique ɸ2 engendré par le courant "I2" circulant dans la bobine N°2, à ce moment la bobine N°2 embrasse également un flux ɸ1 créé par le courant "I1" circulant dans la bobine N°1.
Le coefficient d’inductance mutuelle "M12" de la bobine N°1 par rapport à la bobine N°2 s’exprime par le rapport :
On a également :
et on démontre que :
Inductances sur Fer :
L’inductance sur fer permet d’atteindre des valeurs élevées parce que le matériau ferromagnétique sur lequel est placé le bobinage augmente la perméabilité du système : on a des matériaux comme le numétal qui permettent d’atteindre des µ de 100.000.
Cependant ce résultat entraîne des inconvénients : le premier de ceux-ci est la non-linéarité due au CYCLE D’HYSTÉRÉSIS (Fig. 2), le second consiste dans les pertes que présentent de tels circuits.
Rappelons que la perméabilité est donnée par :
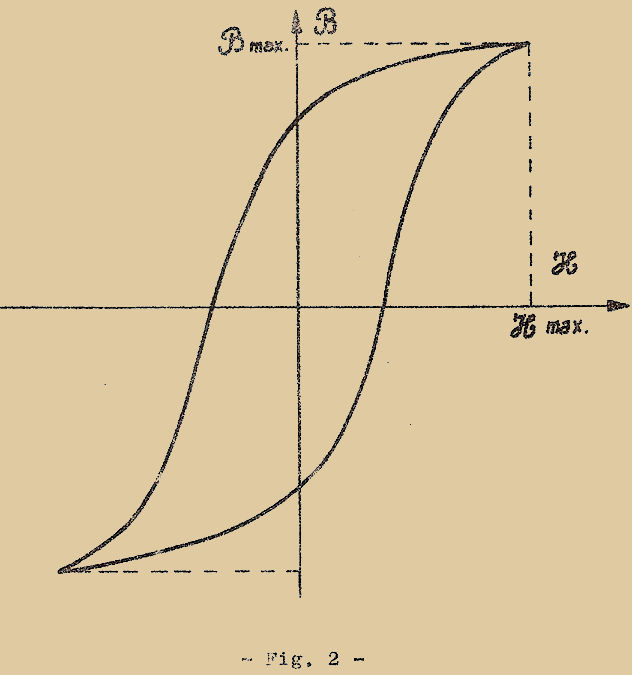
En outre la perméabilité des corps ferromagnétiques décroît quand la température augmente ; le ferromagnétisme vient même à disparaître pour une température caractéristique propre à chaque matériau : c’est le POINT DE CURIE qui se trouve généralement aux environs de 500°C.
LES PERTES dans les circuits magnétiques sont un facteur fondamental pour les mesures, puisque si l’on n’en tient pas compte ou si l’on ignore les correctifs à apporter, on introduit des erreurs non négligeables.
Analysons ces différentes pertes d’origines diverses qui ne se produisent d’ailleurs qu’en régime variable.
a) Pertes par Hystérésis :
La forme de la courbe de première aimantation (premier cycle d’hystérésis) montre que l’induction est loin d’être une fonction linéaire du champ magnétique :
Le parcours d’une boucle d’hystérésis, entraîne une dépense d’énergie proportionnelle au volume magnétique et à la surface du cycle.
b) Pertes par courants de Foucault :
Ces pertes proviennent de la circulation des courants induits dans le circuit magnétique dont la résistivité n’est pas nulle.
Les pertes Foucault sont proportionnelles au volume du circuit magnétique, à sa conductibilité électrique, au carré de la fréquence, et au carré de l’induction maximum ainsi qu’à la plus petite dimension du circuit : ceci explique pourquoi on a toujours intérêt à FEUILLETER les circuits magnétiques.
LES TRANSFORMATEURS
Le transformateur PARFAIT est caractérisé par le rapport de transformation "n" :
où :
- n1 représente le nombre de spires du primaire
- n2 représente le nombre de spires du secondaire
- L1 représente l’inductance du primaire
- L2 représente l’inductance du secondaire
Si le couplage entre les deux inductances n’est plus parfait, une partie du flux émis par un enroulement ne traverse plus la totalité de l’autre, et le transformateur présente des FUITES ; dans ce cas :
où "ℓ1" et "ℓ2" représentent les inductances de fuites créées par le flux qui ne contribue pas au couplage et dont la majeure partie passe dans l’air. "LU1" et "LU2" représentent les inductances présentées respectivement par les impédances d’entrée et de sortie.
Un transformateur réel présente donc des pertes dues aux causes suivantes :
- résistance et capacité répartie des enroulements
- capacité répartie entre les enroulements
- pertes propres au circuit magnétique
Les résistances des enroulements font intervenir les courants entrant et sortant des transformateurs : ce sont des résistances en série avec des inductances de fuite.
Les capacités réparties des enroulements se présentent aux bornes d’accès du transformateur : ce sont des capacités mises en parallèle sur l’entrée et la sortie.
Les pertes dans le circuit magnétique sont créées par la circulation du flux de couplage entre enroulements.
On les représente par des résistances en série et en parallèle avec l’inductance magnétisante.
La capacité répartie entre enroulements qui dépend du couplage se résume à une capacité reliant la borne d’entrée à la borne de sortie.
Le schéma équivalent du transformateur est alors celui de la Fig. 3.
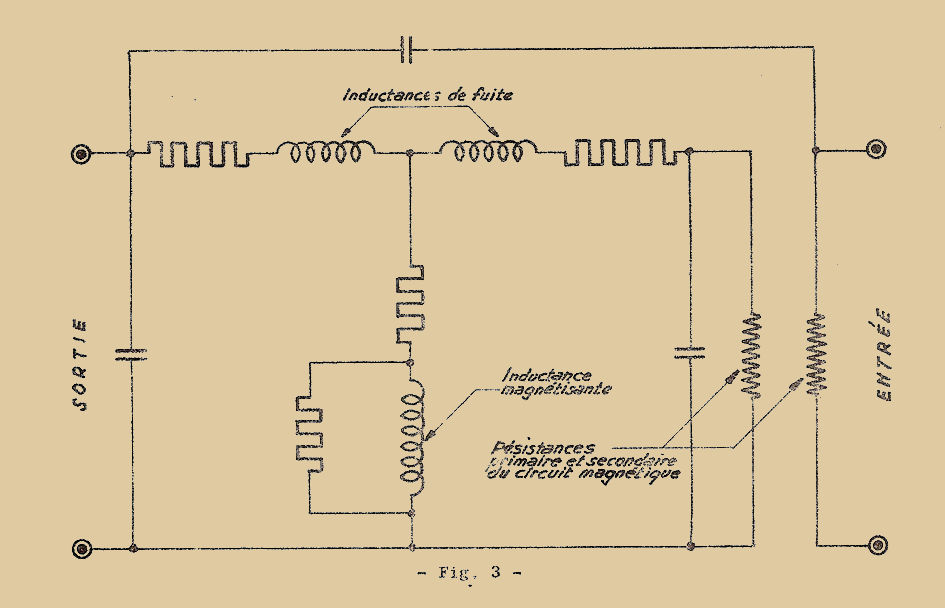
LES PIÈCES DÉTACHÉES DANS LES MESURES (suite)
LES VARISTANCES
Caractéristiques générales :
Les varistances sont des SEMI-CONDUCTEURS à base de silicium qui ont la propriété fondamentale de présenter une résistance variable suivant la tension qui est appliquée aux bornes.
Si l’on appelle "I0" le courant traversant la varistance pour une tension appliquée "U0", on connaîtra le courant de circulation "I" quand on appliquera une tension "U" par la relation suivante :
Le coefficient β est propre au matériau constitutif de la varistance et est en général de l’ordre de 0,2 ; ce qui fait qu’en première approximation le courant "I" est donné par la relation :
On observe que la RÉSISTANCE APPARENTE DE LA VARISTANCE S’EFFONDRE LORSQUE LA TENSION APPLIQUÉE CROÎT ; en effet si dans la relation précédente on remplace :
U/I par "R", résistance pour la tension "U"
U0/I0 par "R0", résistance pour la tension "U0",
on peut écrire :
Si par exemple la tension passe de 10 Volts à 20 Volts, c’est-à-dire si elle est doublée, le rapport U04/U4 est égal à 1/16 et la résistance "R" devient donc le seizième de sa valeur précédente "R0".
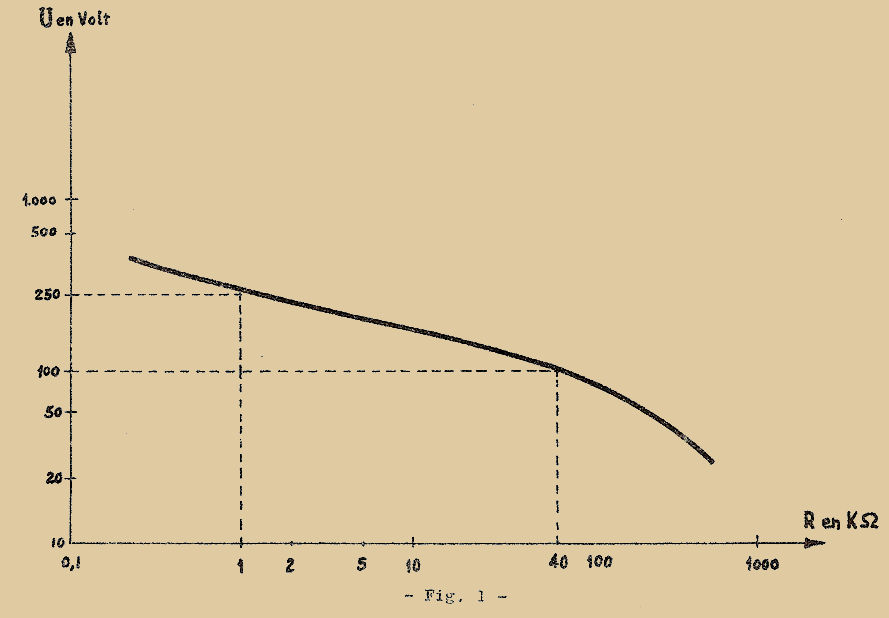
La courbe de la Fig. 1 donne l’allure de cette chute de résistance lorsqu’il y a croissance de la tension aux bornes, et inversement : la varistance présentant une résistance de 1.000Ω pour une tension de 250 Volts, la résistance prend la valeur de 40.000Ω lorsque la tension descend à 100 Volts : il y a bien un rapport de 2,5 (ce qui à la puissance 4ème fait environ 40) et un rapport de résistance de 40.
L’emploi des varistances se généralise dans les circuits où l’on désire se prémunir, des effets brutaux de tension, comme par exemple dans les relais à rupture franche (pare-étincelles) ou bien dans les cas de limitation de forces électromotrices parasites (bobines de relais).
Comme la puissance dissipée par une résistance s’exprime par la relation :
on voit que la PUISSANCE DISSIPÉE CROÎT RAPIDEMENT lorsque la tension augmente puisque simultanément à cette augmentation, il y a chute de la valeur de résistance : lors de l’utilisation d’une varistance, on doit calculer sérieusement la puissance qui y sera dissipée pour éviter la destruction de l’élément.
Ajoutons que le coefficient de température des varistances est NÉGATIF, et de l’ordre de -2.10-3 par degré C : par cette seule caractéristique la puissance dissipée a encore tendance à augmenter lorsque la tension "V" augmente, puisque la valeur propre de la varistance diminue au fur et à mesure qu’elle s’échauffe ; il y a donc EFFET CUMULATIF.
LES REDRESSEURS
Caractéristiques générales :
Les éléments redresseurs sont caractérisés par une conductibilité qui n’a pratiquement lieu que pour un SENS POSITIF de la tension : cette considération subit certaines corrections suivant qu’il s’agisse de REDRESSEUR SEC ou de VALVE ÉLECTRONIQUE : dans le premier cas dès que la tension appliquée change de signe, il n’y a plus circulation de courant mais apparition d’un faible courant négatif ; dans le second cas il y a encore conduction lorsque la tension appliquée change de signe, mais il n’y a jamais apparition de courant négatif (ce qui serait en contradiction avec le principe du tube électronique).
Les courbes représentatives du courant en fonction de la tension sont données à la Fig. 2, tant pour le redresseur sec que pour la valve électronique ; ces deux courbes peuvent s’assimiler à des segments de droite comme le montre la Fig. 3.
L’élément peut alors être caractérisé par :
- sa RÉSISTANCE DIRECTE "Rd"
- sa RÉSISTANCE INVERSE "Ri"
qui mesurent chacune l’INVERSE DES PENTES des deux demi-droites constituant la caractéristique :
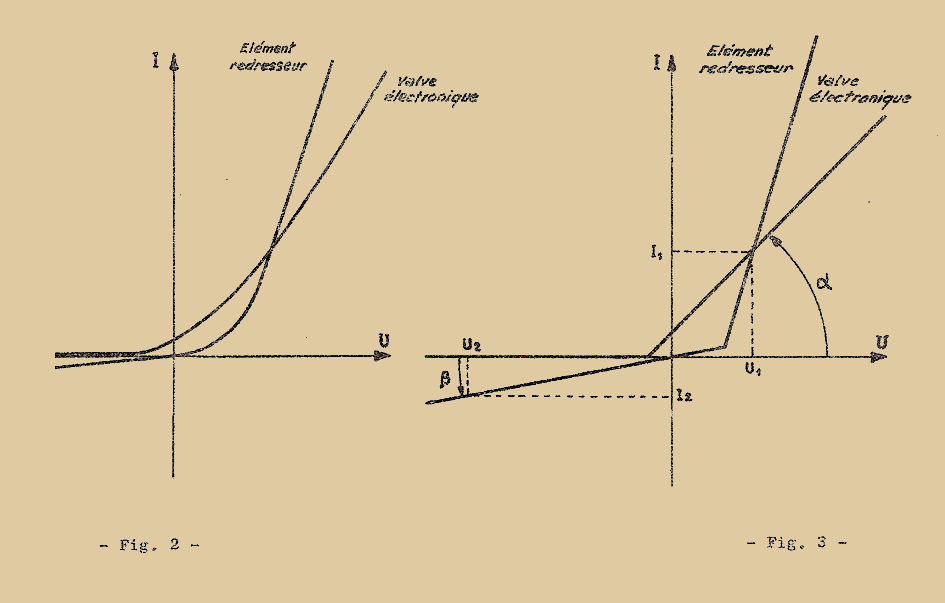
Précisons tout de suite que les résistances "Rd" et "Ri" ne doivent pas être confondues avec les résistances apparentes du redresseur qui seraient mesurées en continu.
Il faut encore préciser pour caractériser pleinement un redresseur :
- L’INTENSITÉ MAXIMUM "Id", mesurée dans le sens DIRECT, que peut supporter l’élément sans risque d’instabilité ou de destruction dû à son échauffement.
- La TENSION MAXIMUM "Ui", mesurée dans le sens INVERSE, que peut supporter l’élément sans risque de claquage.
Les redresseurs peuvent se classer en plusieurs catégories :
- Les diodes à vide pour la détection, la modulation et la démodulation des fréquences plus ou moins élevées.
- Les valves à vide ou à gaz (diodes thermo-ioniques), pour le redressement de la tension secteur, les très fortes tensions ou intensités.
- Les diodes utilisées pour la détection faible, et aussi maintenant (vu leur faible encombrement et leur efficacité en fréquence) pour le redressement dans les appareils de mesure.
- Les cellules redresseuses, utilisées dans le redressement des tensions à basse fréquence.
Nous ne faisons que mentionner ici les diodes à vide de la 1ère catégorie, car nous ne nous préoccupons dans ce chapitre que des éléments redresseurs.
Cellules Redresseuses :
Les cellules redresseuses appelées souvent REDRESSEURS SECS, utilisent le phénomène de MOBILITÉ très différente des électrons dans le métal et le semi-conducteur : lorsque le potentiel du semi-conducteur est supérieur à celui du métal, les électrons passent facilement du métal dans le semi-conducteur et il y a circulation de courant ; lorsque le potentiel du semi-conducteur est inférieur à celui du métal, les électrons situés initialement dans le semi-conducteur, et trouvant des BARRIÈRES à franchir pour circuler, ne passent que très difficilement dans le métal. On illustre ceci en disant qu’il y a une COUCHE D’ARRÊT entre le métal et le semi-conducteur.
Les redresseurs secs, composés donc d’un métal et d’un semi-conducteur, sont le plus souvent de deux types :
- Cuproxyde : cuivre et oxyde de cuivre
- Sélénofer : sélénium et oxyde de fer.
Les tensions redressées suivant le nombre de cellules accolées les unes aux autres varient de quelques Volts à plusieurs kilovolts ; de même suivant le type de redresseur utilisé, l’intensité du courant varie de quelques Milliampères à plusieurs kiloampères : évidemment lorsqu’il s’agit de fortes intensités on munit les redresseurs d’ailettes de refroidissement de très grandes surfaces pour assurer une bonne dissipation de la chaleur.
Ces éléments sont très sensibles à la température ambiante et ne peuvent pas en général être utilisés au-delà de 80°C.
Le coefficient de température des résistances "Ri" et "Rd" étant négatif, il y a là aussi effet cumulatif pour la puissance consommée.
L’efficacité varie beaucoup avec la fréquence, et les redresseurs secs de modèle courant ne peuvent pas aller au-delà de 20kHz.
Les diodes à cristaux :
Ces diodes utilisent l’effet de conductibilité unilatérale qui apparaît pour un contact ponctuel entre une pointe métallique qui constitue l’anode et un cristal SEMI-CONDUCTEUR qui sert de cathode (semi-conducteur au germanium ou au silicium) : ce sont les DIODES A POINTE. Si le semi-conducteur est du type "P" le sens passant est inversé du précédent.
S’il s’agit de redresser des courants importants, on utilise des DIODES A JONCTION.
En raison des faibles capacités parasites qu’elles présentent, ces diodes sont utilisables jusqu’à des fréquences pouvant atteindre plusieurs centaines de MHz et même plusieurs milliers de MHz si le semi-conducteur est du silicium.
Voici les caractéristiques de certains types de diodes dont on voit que le courant direct passe de quelques mA à plusieurs Ampères.
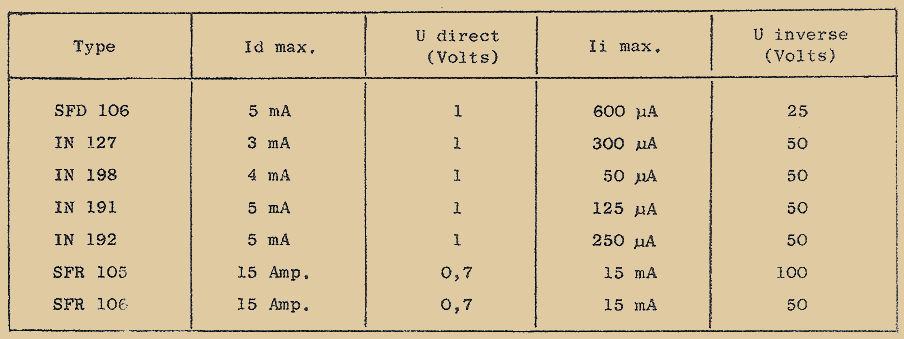
Bien entendu les semi-conducteurs étant sensibles à la chaleur, surtout s’il s’agit de germanium, on doit éviter toute surpuissance et limiter les mesures pour une température ambiante d’environ 45°C.
Valves à vide ou à gaz :
Dans ces éléments, l’effet de redressement est dû au fait que les électrons issus d’une cathode thermo-émissive ne pourront atteindre l’anode que si celle-ci est placée à un potentiel suffisamment élevé : en l’absence de champ électrique croissant, les électrons sont arrêtés sous l’influence de la CHARGE D’ESPACE négative que constituent les électrons dont la densité croît au fur et à mesure que l’on se rapproche de la cathode. La Fig. 4 représente la courbe courant-tension d’une DIODE A VIDE.
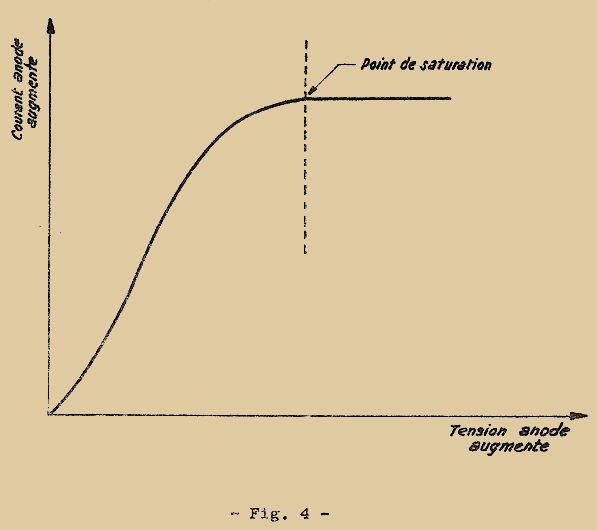
S’il s’agit maintenant d’une DIODE A GAZ (Fig. 5), il y a IONISATION du gaz (ou de la vapeur, ex : mercure) et les ions positifs formés vont neutraliser la charge d’espace négative : il y aura donc pratiquement plus d’obstacle au déplacement des électrons. La charge d’espace ainsi neutralisée, des courants considérables pourront traverser le tube dont l’anode n’aura pas besoin d’être à un potentiel élevé. (Par contre coup, les ions positifs reviennent bombarder la cathode, ce qui finit à la longue par provoquer sa destruction).
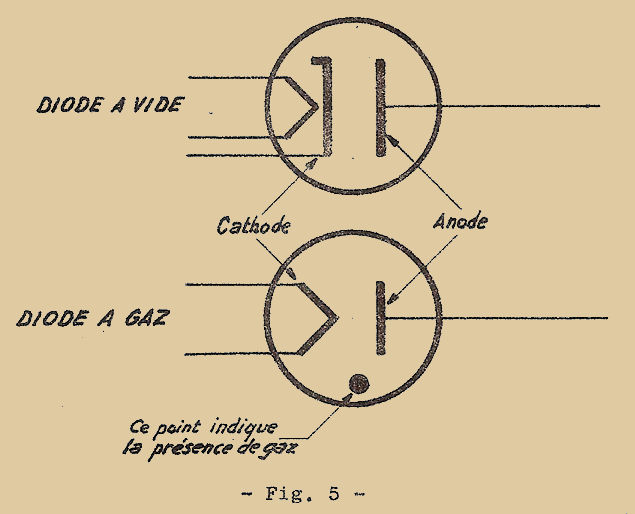
Les valves sont destinées à fournir des débits importants. Les valves à vide présentent une résistance directe notable, la chute de tension étant de l’ordre de 50 Volts pour un débit maximum de 30 à 120 mA moyens. Les valves à gaz permettent, grâce à l’ionisation du milieu, des débits beaucoup plus importants (plusieurs dizaines d’Ampères) sous une chute de tension inférieure à 15 Volts, cependant le fonctionnement des valves à gaz, surtout s’il s’agit de vapeur de mercure, sont très sensibles à la température.
Les tensions inverses des valves varient selon le type de 1000 Volts à des dizaines de kilovolts.
Les résistances directes sont de l’ordre de quelques kΩ, et les résistances inverses pratiquement infinies.
Il existe encore un autre type de valve à gaz : LA DIODE À CATHODE FROIDE (Fig. 6).
Le fonctionnement d’un tube à cathode froide est basé sur le fait que dans un gaz il y a quelques ions présents : si la pression est suffisamment basse, un potentiel modéré donnera assez de vitesse à ces ions pour que ceux-ci fassent naître par chocs de nouveaux ions dans le gaz et ainsi de suite : cet effet cumulatif rend le tube conducteur sans qu’aucune chaleur ne soit fournie à la cathode.
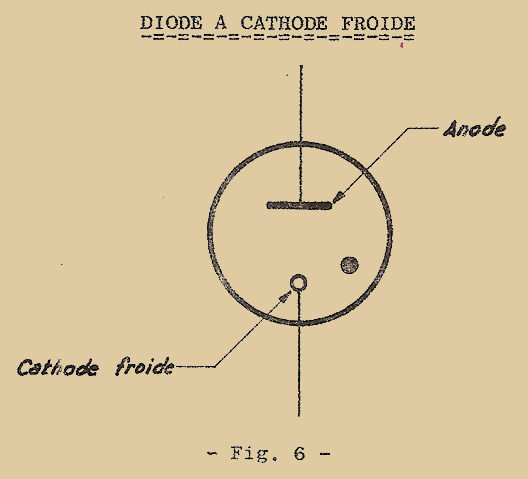
Puisque le passage du courant dans un tel tube est rendu possible par la présence continuelle d’ions dans le gaz, et non par des électrons émis par chauffage, les deux éléments peuvent servir de cathode suivant la polarité qui leur est appliquée.
Les tubes à cathode froide peuvent être construits de façon à ne conduire le courant que dans un seul sens : ceci est réalisé en prenant une anode de très faible surface et une cathode de grande surface ; l’anode sera alors constituée d’un fil fin et la cathode aura la forme d’un cylindre.
Contrairement aux tubes à vide, dans un tube à cathode froide la chute de potentiel reste pratiquement constante quelle que soit l’intensité du courant qui traverse le tube. Cette propriété est très utile dans les circuits, surtout lorsqu’il s’agit de mesures, POUR RÉGULER LA TENSION : la Fig. 7 schématise un tel circuit.
Une variation de la tension d’alimentation fait varier le courant dans "R" et le tube régulateur ; il y a donc variation du potentiel à travers "R" mais la chute de potentiel à travers le tube restant pratiquement constante, il en est de même pour la tension de sortie prise aux bornes du tube.
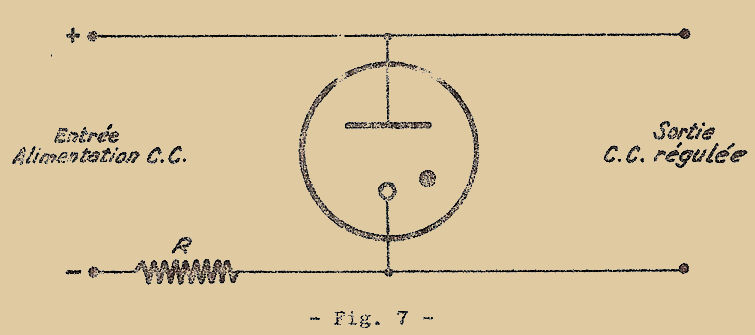
Ainsi se termine notre rapide exposé sur les pièces détachées utilisées dans les mesures ; on aura noté l’absence des tubes électroniques dont on parlera prochainement dans deux leçons théoriques.
Les leçons suivantes de Métrologie se rapportent directement aux mesures, méthodes et précisions, des paramètres les plus courants en électronique.
LA MESURE DES COURANTS
Pour établir le calcul des courants de circulation dans un circuit quelconque, il est souvent nécessaire d’appliquer les LOIS DE KIRCHHOFF et nous commencerons par exprimer les notions élémentaires sur la théorie des réseaux.
LES RÉSEAUX
Supposons que des conducteurs linéaires soient réunis entre eux par des liaisons quelconques de façon à fournir UN RÉSEAU DE CONDUCTEUR analogue, par exemple, à celui que représente la Fig. 1.
On appelle NŒUD d’un réseau un point commun à au moins trois circuits compris dans le réseau : le point "C" est un nœud.
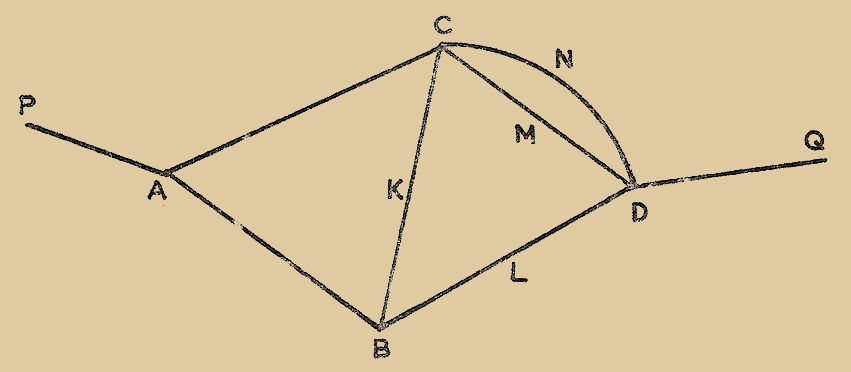
Fig. 1
On appelle BRANCHE d’un réseau un circuit reliant deux nœuds sans passer par un nœud intermédiaire : le segment "M" est une branche.
On appelle MAILLE d’un réseau un circuit fermé passant par plusieurs nœuds : le triangle "C B D" comprenant les nœuds "C", "B", "D" et les branches "K", "L", "M" est une maille.
LOIS DE KIRCHHOFF
Considérons un nœud tel que "C" : lorsque le régime permanent est atteint, la charge portée par les portions de conducteurs qui l’environnent reste constante.
La quantité d’électricité qui arrive à chaque instant au point "C" est donc égale à celle qui s’en éloigne ; c’est ce qu’exprime la première loi de Kirchhoff : LA SOMME DES INTENSITÉS DES COURANTS QUI S’APPROCHENT D’UN NŒUD DU RÉSEAU EST ÉGALE À LA SOMME DES INTENSITÉS DES COURANTS QUI S’EN ÉLOIGNENT.
Examinons la Fig. 2 et choisissons pour sens positif sur chaque conducteur le sens qui s’éloigne du point "C" : l’intensité du courant électrique qui le parcourt sera considérée comme grandeur positive quand le courant circule dans le sens positif, comme grandeur négative quand le courant circule dans le sens négatif.
On peut dire, d’après les flèches de la figure indiquant le sens positif et exprimant par-là que tous les courants s’éloignent du point "C", que : la somme algébrique des intensités des courants qui s’éloignent d’un nœud du réseau est NULLE.
C’est toujours la première loi de Kirchhoff qui permet de l’affirmer, puisque dans notre exemple les intensités des courants qui RENTRENT dans le nœud sont égales à zéro et que par conséquent les intensités des courants qui en SORTENT et qui leur sont égales sont donc nulles.
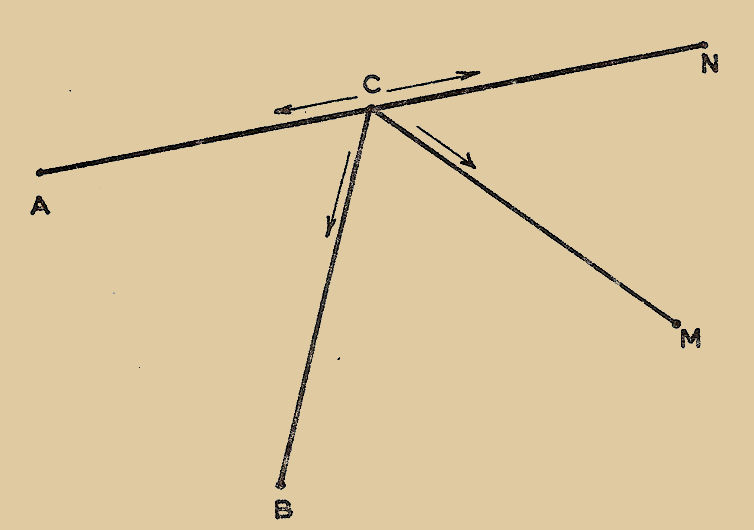
Fig. 2
On symbolisera cette évidence par l’égalité :
Ʃi = 0 (rappelons que Ʃi se lit "somme de i" et exprime la somme algébrique des intensités).La seconde loi de Kirchhoff nous dit que LORSQUE PLUSIEURS CONDUCTEURS FORMENT UNE MAILLE, LA SOMME ALGÉBRIQUE DES PRODUITS DE LA RÉSISTANCE DE CHAQUE CONDUCTEUR PAR L’INTENSITÉ DU COURANT QUI LA PARCOURT EST NULLE, autrement dit que la somme des différences de potentiel rencontrées le long d’une maille est nulle.
Considérons la Fig. 3 où l’on a représenté la maille "C B D" qui est bien un circuit fermé ; supposons que les sens positifs choisis sur chaque conducteur soient ceux qu’on obtient en parcourant le circuit dans le sens "C B D" et appliquons la loi d’Ohm à chaque conducteur, on a :
En les rajoutant membre à membre, on obtient la seconde loi de Kirchhoff :
On exprimera cette égalité par la relation :
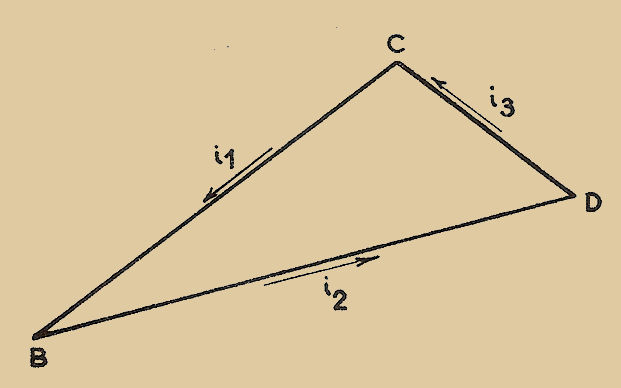
Fig. 3
Ainsi, pour trouver la distribution des courants dans un réseau de conducteurs, on prendra des sens positifs arbitraires sur chacun des conducteurs et on écrira les différentes relations de Kirchhoff pour les différents nœuds et pour les différentes mailles que l’on peut constituer.
APPLICATION : Courants Dérivés
Supposons qu’un circuit parcouru par un courant soit bifurqué entre deux points "C" et "D".
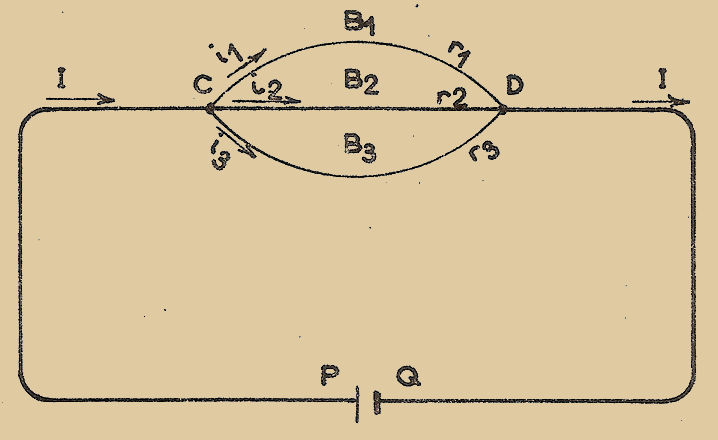
Fig. 4
Le courant "I" arrivant par le conducteur "PC" se partage en "C" entre différentes branches "B1", "B2" et "B3" qui se rejoignent au nœud "D" puis s’écoule ensuite par le conducteur "DQ".
On dit alors que les branches "B1", "B2", "B3" sont disposées en DÉRIVATION.
La première loi de Kirchhoff appliquée au point "C" ou au point "D" donne la même équation, avec comme sens positifs des courants ceux qu’indiquent les flèches :
La seconde loi devra être appliquée successivement aux différents circuits tels que "CB1D, CB2D, CB3D" :
que l’on peut écrire :
ou encore, ce qui ne modifie pas le quotient :
Remplaçons "i1 + i2 + i3" par "I", on a finalement
Nous aurons une illustration pratique de la relation fondamentale en l’appliquant à l’APPAREIL DE MESURE des courants (galvanomètre ou microampèremètre) entre les bornes duquel est placée en dérivation une résistance ou SHUNT.
La Fig. 5 montre le dispositif réalisé pour utiliser un appareil à la mesure d’un courant "I" SUPÉRIEUR à celui qu’il peut supporter en bout d’échelle.
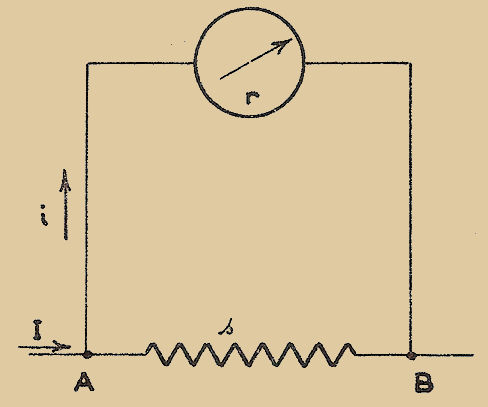
Fig. 5
Pour obtenir la valeur de "I", il faudra multiplier les indications de l’appareil par un nombre "m" qui est le rapport " I/i " du courant total au courant qui traverse le galvanomètre et qu’on peut calculer si l’on connaît les résistances "r" et "s" du galvanomètre et du shunt.
On a :
On pourra écrire en prenant la première et la troisième égalité :
et comme "m = I/i ", on aura :
ou :
Si l’on veut par exemple que "m" soit égal à 100, il suffira de prendre :
Dans la pratique, il n’y a pour ainsi dire pas une seule mesure de courant dans laquelle il ne soit pas fait usage d’un shunt soit que l’opérateur le place lui-même, soit que le constructeur l’ait déjà inclus dans l’appareil.
Les ampèremètres à cadre mobile par exemple donnent en général une déviation correspondant à toute l’échelle lorsque le cadre est traversé par un courant de quelques milliampères : il faut shunter le cadre pour mesurer des courants supérieurs et on peut mesurer un courant quelconque de 1.000 ampères si l’on veut en choisissant convenablement la résistance du shunt.
Lorsqu’on utilise un shunt extérieur, il faudra veiller à ce que les résistances propres des cordons de liaison entre le galvanomètre et le shunt soient bien compris dans le calcul de la résistance "r" du galvanomètre, et on se préoccupera de réduire toutes les résistances de contact à des valeurs négligeables.
LES DIVERSES MÉTHODES DE MESURE DES COURANTS
Pour assurer un courant, on peut faire appel à une méthode de déviation directe (cas le plus fréquent) ou à d’autres méthodes.
a – MÉTHODE DE DÉVIATION DIRECTE
Cette méthode consiste à insérer en série dans le circuit un ampèremètre pour mesurer un courant.
Les appareils en jeu peuvent être à action directe, ce qui est le cas le plus souvent dans les mesures aux fréquences industrielles : nous avons examiné dans la 5ème leçon de Métrologie la classification de tels appareils.
Les appareils peuvent être aussi à action indirecte, appareils à redresseurs, à diode, à thermocouple, à amplificateur ou même hétérodynes : c’est le cas le plus fréquent dans les mesures en courant alternatif à fréquence supérieure aux fréquences industrielles, ainsi qu’en régime non alternatif.
Un cas très particulier d’appareil à action indirecte est l’oscilloscope cathodique.
b – AUTRES MÉTHODES
Les autres méthodes utilisables sont celles de déviation, substitution et les méthodes de zéro. Ces dernières procèdent par opposition et sont applicables tant en courant continu qu’en alternatif : elles relèvent du LABORATOIRE DE MÉTROLOGIE plutôt que de la pratique courante et sont donc d’emploi délicat.
L’ampèremètre ayant une impédance "Z" sera parcouru, lorsqu’il aura été inséré dans le réseau, par un courant " I’ " donné par la relation :
comme on l’a vu plus haut, "I" étant le courant de circulation à mesurer et "Z" l’impédance du shunt total et par conséquent du circuit sur lequel est branché l’appareil.
On en conclut immédiatement qu’un ampèremètre doit présenter une IMPÉDANCE FAIBLE vis-à-vis de l’impédance interne du réseau vu des bornes entre lesquelles on l’insère.
La valeur absolue de l’ERREUR SYSTÉMATIQUE relative commise en négligeant de corriger la lecture faite sur un ampèremètre SUPPOSÉ infiniment précis est sensiblement égale au rapport entre l’impédance de l’ampèremètre et l’impédance du réseau.
LE GALVANOMÈTRE FONDAMENTAL
Le galvanomètre fondamental est le galvanomètre DEPREZ-d’ARSONVAL : c’est le type même des ampèremètres magnéto-électriques à cadre mobile et à aimant fixe, destinés à fonctionner en courant continu.
C’est un appareil à suspension dans lequel le fil de torsion en argent amène le courant à mesurer à un cadre mobile dans un champ magnétique radial créé dans l’entrefer d’un aimant à pôles cylindriques et d’un cylindre de fer doux suspendu à l’intérieur du cadre (voir Fig. 6).
Ce fil de torsion est solidaire d’une part du bâti du galvanomètre à sa partie inférieure, d’autre part d’un bouton tournant à frottement doux à sa partie supérieure et permettant ainsi le réglage du zéro de l’appareil et celui de la torsion du fil.
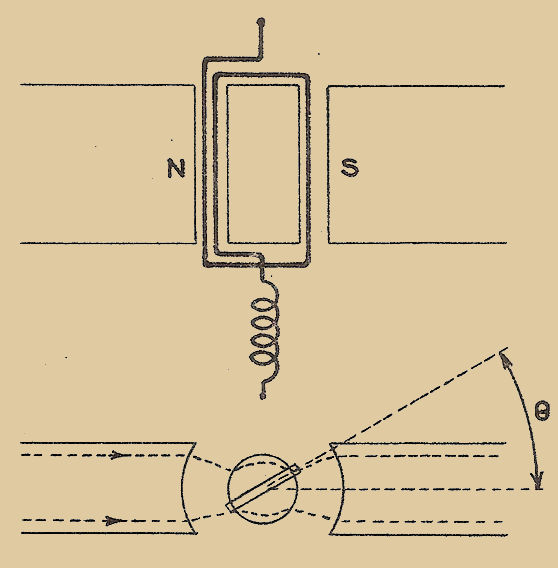
Fig. 6
On voit sur la figure que sous l’action d’un courant "I", il y a rotation du cadre autour de son axe d’un angle θ : on mesurera cet angle et donc le courant par réflexion d’un point lumineux sur un miroir placé verticalement sur le cadre.
L’inconvénient de cet appareil est son encombrement et sa fragilité de par sa très grande sensibilité : on ne l’emploie principalement que dans des mesures en courant continu utilisant une méthode d’opposition.
En pratique on se servira du MICROAMPÈREMÈTRE qui n’en diffère que par le fait que le fil de torsion qui suspend l’équipage mobile et lui amène le courant est remplacé par un pivotage et une paire de spiraux bandés en opposition : ces spiraux fournissent le couple antagoniste et servent de conducteurs d’amenée et de sortie du courant ; en outre le miroir est remplacé par une aiguille.
PARAMÈTRES ET RELATIONS FONDAMENTALES DU GALVANOMÈTRE À CADRE MOBILE
L’établissement de l’équation fondamentale du galvanomètre et sa discussion sortiraient du cadre de ces leçons : nous nous contenterons d’énoncer les relations les plus importantes auxquelles on pourra faire appel lors d’interprétation de mesures précises.
a – LA DÉVIATION du galvanomètre est rigoureusement proportionnelle à l’intensité qui le traverse :
"a" étant une constante propre à l’appareil et dépendant notamment de son couple de torsion.
b – LA SENSIBILITÉ σ = θ/I est proportionnelle au champ magnétique de l’aimant permanent, au nombre de spires et à la surface du cadre. Comme pour un volume de conducteur donné, donc pour un cadre de dimensions données, la résistance est proportionnelle au carré du nombre de spires, on peut affirmer que la sensibilité est PROPORTIONNELLE À LA RACINE CARRÉE DE LA RÉSISTANCE du galvanomètre.
b – LA PÉRIODE propre du galvanomètre est proportionnelle à la racine carrée du moment d’inertie de l’équipage mobile ; elle est donc donnée par la relation :
On pourra aussi écrire la formule donnant "T0" sous la forme :
où "Ce" désigne cette fois l’élasticité du système, c’est-à-dire l’inverse du couple de torsion.
On remarquera immédiatement l’analogie avec la formule donnant la période d’oscillation d’un circuit oscillant :
où ici "L" représente l’inductance et "C" la capacité du circuit.
LA MESURE DES TENSIONS
De même que lors de la mesure des courants, pour mesurer une tension on peut employer une méthode de déviation directe (cas le plus courant) ou d’autres méthodes, dites de déviation-substitution, ou de zéro.
La méthode de déviation directe consiste alors à placer l’appareil en déviation pour mesurer la tension, et non plus en série comme c’était le cas de l’ampèremètre pour la détermination du courant.
LES VOLTMÈTRES
MESURE DE TENSION PAR APPLICATION DE LA LOI D’OHM :
Un voltmètre est constitué par un MICROAMPÈREMÈTRE de résistance "r" en série avec une résistance fixe "R" qui dépend du calibre de l’appareil et des caractéristiques du microampèremètre.
Le microampèremètre mesure le petit courant "i" qui traverse la résistance "R + r". La tension indiquée par l’appareil est donc :
Pour chaque CALIBRE d’un appareil à plusieurs calibres la déviation maximum est obtenue pour un courant déterminé "i0" traversant le voltmètre. Ce courant caractérise l’appareil. Mais la résistance d’un voltmètre est un élément fondamental de l’appareil, on préfère considérer "1⁄i0" qu’on exprime en ohms par volts et qui exprime la sensibilité de l’instrument. Pour les appareils usuels "1⁄i0 " est compris entre 300Ω/V pour les instruments utilisés pour des mesures sur des circuits très peu résistant ("i0 = 3,3mA"), et 2.104Ω/V pour les appareils les plus poussés ("i0 = 50µA").
De tels appareils ont un coefficient de température qui peut ne pas être négligeable ; on le réduit au maximum en bobinant la résistance en série en manganine ou en constantan.
Si on désigne par "α1 et α2" les coefficients de température respectivement de "r" et "R", on a :
et :
"r0" et "R0" étant les résistances à 0°C.
Pour une température "t" donnée, la variation de "r" est "r0.α1.t" et la variation de "R" est "R0.α2.t". La variation globale des deux résistances en série est donc :
Définissons par "α" le coefficient de température de l’appareil, on a bien :
ou en simplifiant :
ou encore :
Le coefficient "α" est d’AUTANT PLUS PETIT que r0/R0, ou r/R , est PLUS PETIT : on a donc toujours intérêt à avoir LA RÉSISTANCE "R" DU CADRE LA PLUS ÉLEVÉE POSSIBLE.
Il est bien évident que si les coefficients de température des deux résistances sont égales, "α1 = α2 = α’" (matériaux identiques), le coefficient de température de l’appareil sera précisément égal au coefficient des deux résistances :
LES VOLTMÈTRES ÉLECTROSTATIQUES
Un voltmètre électrostatique ou ÉLECTROMÈTRE est essentiellement constitué par un condensateur variable.
L’énergie électrostatique d’un condensateur soumis à une tension "U" étant :
on sait que le couple "K" auquel est soumis le rotor du "C.V." est proportionnel à l’énergie :
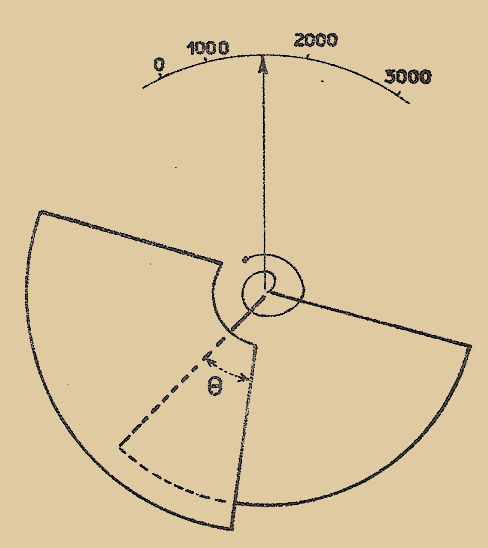
Fig. 1
On dispose donc un plateau mobile en équilibre stable entre deux faces planes (quadrants) en le suspendant en son centre par un fil fin ou encore en le faisant pivoter sur un axe (Fig. 1) : en appliquant une tension aux bornes des lames fixe et mobile, il y aura rotation de cette dernière ; LA DÉVIATION étant proportionnelle à l’énergie emmagasinée le SERA ÉGALEMENT AU CARRÉ DE LA TENSION que l’on pourra ainsi mesurer.
Le voltmètre électrostatique est à peu près le seul appareil employé pratiquement pour la mesure des différences de potentiel comprises entre 1.000 et 15.000Volts.
Il a l’avantage de n’être influencé, ni par les courants, ni par les champs électriques et magnétiques voisins. Comme sa déviation ne dépend que du carré de la différence de potentiel, il peut mesurer indifféremment des différences de potentiel continues ou alternatives : dans ce dernier cas il en donnera la valeur efficace, et ses indications sont indépendantes de la fréquence.
Son inconvénient est celui de tous les appareils où la déviation est proportionnelle au carré de la grandeur à mesurer : les divisions de l’échelle voisines du zéro sont extrêmement resserrées.
La tension applicable à un voltmètre électrostatique étant limitée supérieurement par la RIGIDITÉ DIÉLECTRIQUE entre armatures, il convient pour la mesure des tensions élevées de diviser la tension à mesurer pour l’appliquer à l’électromètre.
Examinons la Fig. 2 : soit "U" la tension à mesurer par l’électromètre "E" auquel on ne peut appliquer sans risque de destruction qu’une tension U/n.
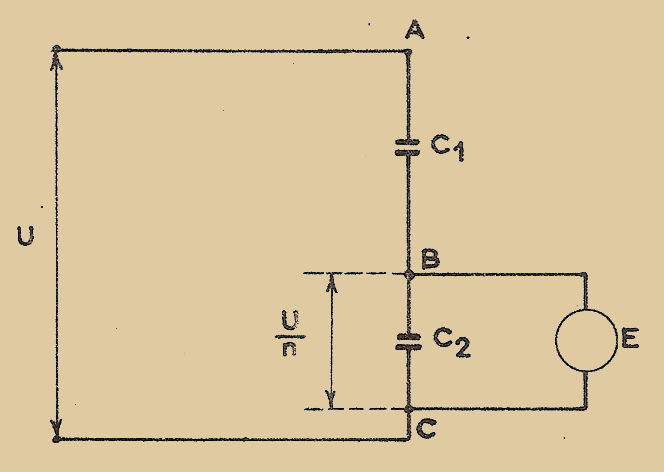
Fig. 2
La différence de potentiel entre "A" et "B" est donnée par :
soit :
La quantité d’électricité circulant ente "A" et "B" doit être la même qu’entre "B" et "C" :
ou en remplaçant "Q" par la relation "Q = capacité x Tension" :
soit :
ou encore :
Donc si l’on désire réduire la tension appliquée à un électromètre dans un rapport "n", on devra choisir des valeurs de capacités de condensateurs shunt et série telles qu’elles soient dans le rapport :
L’association de "C2" et "C1" est ce que l’on appelle un DIVISEUR CAPACITIF.
Pour éviter des erreurs de mesures, on préfère pratiquement superposer à la tension "U" une tension auxiliaire "U0" et procéder à deux équilibres successifs, l’un lors de l’application de la tension "U0" parfaitement connue et stable, l’autre lors de l’application de la tension "U0 + U".
APPAREILS À REDRESSEURS
Les appareils magnéto-électriques à redresseurs ont des caractéristiques voisines de celles des appareils magnéto-électriques en ce qui concerne la chute de tension des ampèremètres et la résistance des voltmètres.
Les redresseurs sont montés soit en simple alternance (Fig. 3a) soit en pont (Fig. 3b), soit en va et vient (Fig. 3c) ce qui dans ce dernier cas implique l’emploi d’un transformateur.
Les indications de ces appareils à redresseurs dépendent de la fréquence en ce sens que les redresseurs sont shuntés par leur capacité interne : il en résulte que l’EFFET DE REDRESSEMENT DIMINUE QUAND LA FRÉQUENCE AUGMENTE.
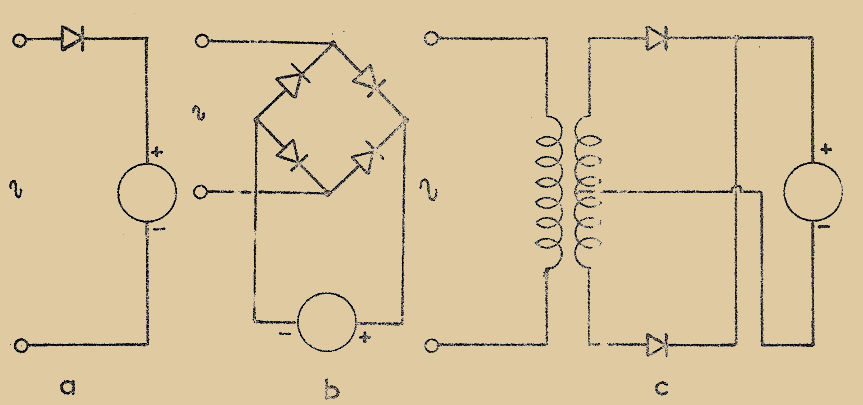
Fig. 3
Ces appareils ont également un coefficient de température non négligeable dû au déplacement notable du coude de la caractéristique des redresseurs en fonction de l’échauffement.
LES VOLTMÈTRES DE CRÊTE À DIODE
Ces voltmètres, nous le verrons par ailleurs dans les leçons Théoriques, mesurent la valeur des crêtes positives des tensions qui leur sont appliquées : il en résulte que leurs indications sont très influencées par la forme des tensions qui leur sont appliquées ; en particulier elles dépendent des harmoniques des tensions sinusoïdales. Un voltmètre à diode gradué en valeurs efficaces de tension commet une erreur de 9,5% dans la mesure d’une tension alternative "U".
Une autre caractéristique des voltmètres à diode est leur impédance d’entrée élevée : en haute fréquence cette impédance d’entrée se trouve shuntée de façon appréciable par la capacité parasite de la diode qui est de l’ordre de quelques pF.
L’erreur qui en résulte sur les indications de l’appareil croît avec la fréquence et en limite l’utilisation à des fréquences inférieures à quelques dizaines de MHz.
Comme la capacité des diodes à cristal est plus faible (de l’ordre de 1pF) que celle des diodes thermo-ioniques, on préfère les employer lorsqu’il s’agit de mesurer des tensions à des fréquences élevées : on peut aller jusqu’à plusieurs centaines de MHz avec des diodes au germanium et plusieurs milliers avec des diodes au silicium.
Comme le voltmètre à diode thermo-ionique, ou voltmètre à lampe, sera longuement étudié dans cette partie du Cours de Mesures, nous n’allons qu’en décrire brièvement le principe.
Le voltmètre à lampe de la Fig. 4 consiste en un pont de Wheatstone dans un bras duquel est placée une triode. Le pont est équilibré en l’absence de tension appliquée à l’appareil, l’application d’une tension à ses bornes d’entrée polarise négativement la grille de la triode par rapport à la cathode, ce qui déséquilibre le pont : un microampèremètre "G" lit le courant de déséquilibre qui est sensiblement proportionnel à la tension d’entrée.
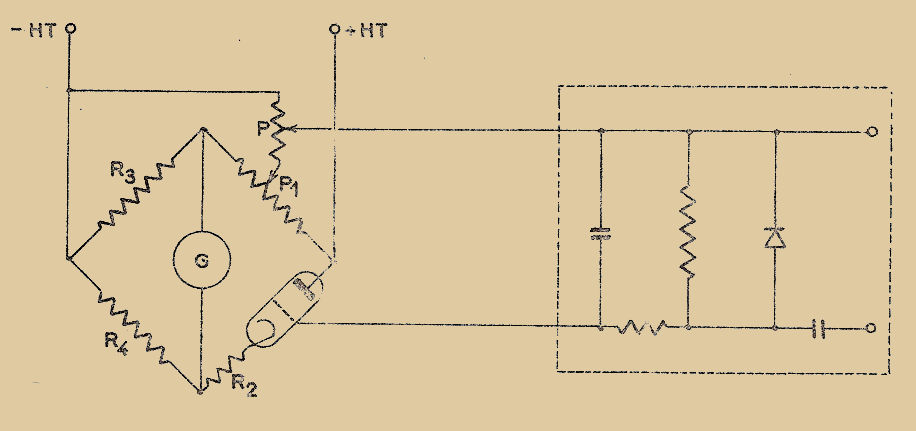
Fig. 4
Le potentiomètre "P" sert à ajuster l’équilibre du pont en l’absence de la tension appliquée et permet donc le réglage du zéro ; des ajustements sur "P1", "R2" et "R3" permettent d’assurer une stabilité relative du zéro lors des changements de sensibilité.
La partie du montage encadrée en pointillé sur le schéma, est contenue dans une tête, ou SONDE, blindée et reliée à l’appareil par un câble blindé qui amène en outre le courant de chauffage du filament : on s’affranchit ainsi des courants parasites lors des mesures en "H.F.".
Bien d’autres montages, que nous verrons par ailleurs, trouvent leur emploi dans les voltmètres à lampe, en particulier ceux qui utilisent des doubles triodes dont on mesure le déséquilibre des courants plaque, déséquilibre qui ne dépend que de la différence de potentiel entre les grilles.
Un inconvénient dû au montage à une diode provient de ce que la cathode émettant des électrons à grande vitesse, une partie de ceux-ci parviennent à la plaque sans que sur celle-ci soit appliquée de tension : ces mêmes électrons retournant à la cathode à travers "R" (Fig. 5) donnent lieu à une tension de déséquilibre indésirable.
La méthode utilisée pour éliminer cet inconvénient majeur consiste à employer une seconde diode identique à la première de façon à produire une tension analogue mais de signe opposé, ce qui annulera la première ; le circuit de principe est donné Fig. 6 ; en réglant "R" on peut faire en sorte que la tension "au repos" introduite par "D2" soit de valeur égale à celle fournie par "D1".
Comme ces deux tensions sont en série, elles s’annulent naturellement.
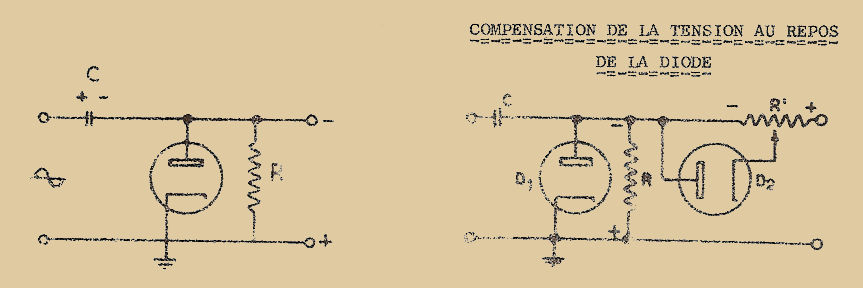
Fig. 5 et 6
On préfèrera toujours utiliser une seconde diode au lieu d’une source de tension fixe pour contrebalancer la tension au repos de "D1" parce que celle-ci dépend de la température de sa cathode, donc de la tension de chauffage et par conséquent varie avec le secteur : si la diode "D2" est identique à "D1", les variations se trouvent en opposition et ne perturberont pas la stabilité du zéro.
LA MESURE DES RÉSISTANCES
La mesure des résistances est une des opérations les plus courantes dans la technique des Mesures Électroniques : on la pratique le plus souvent en courant continu. Les méthodes que l’on applique dépendent surtout de la grandeur des résistances à mesurer.
CODE DES COULEURS DES RÉSISTANCES AGGLOMÉRÉES
La plupart des résistances utilisées dans les circuits électroniques sont du type aggloméré : on leur a affecté un code de couleurs permettant ainsi un repérage rapide ; en sont privées les résistances bobinées et souvent même les résistances de précision sur le corps desquelles on lit la valeur de la résistance à la température ambiante.
Bien entendu la puissance dissipée par une résistance, dans ses limites de sécurité, étant fonction de sa grandeur, on distingue facilement le wattage autorisé par les dimensions propres de la résistance (Fig. 1).
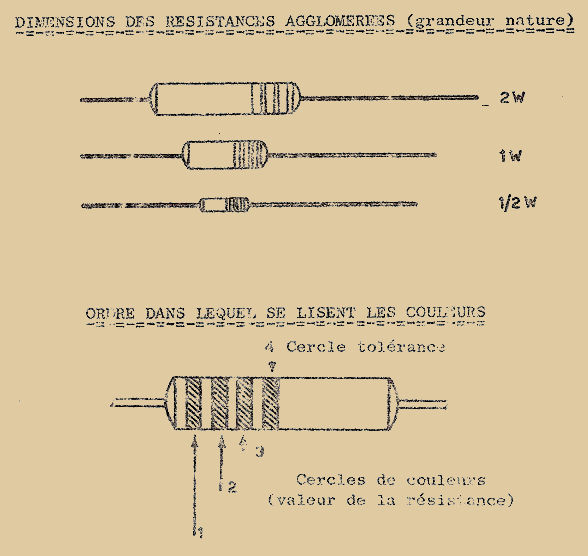
Fig. 1 et 2
La valeur de la résistance est indiquée par des cercles de couleurs qui obéissent à une normalisation bien établie : les trois premiers cercles donnent successivement le premier chiffre, le second chiffre et enfin le nombre de zéros (Fig. 2) ; le quatrième cercle s’il existe indique une tolérance meilleure que 20%, couleur argent pour 10%, couleur or pour 5%.
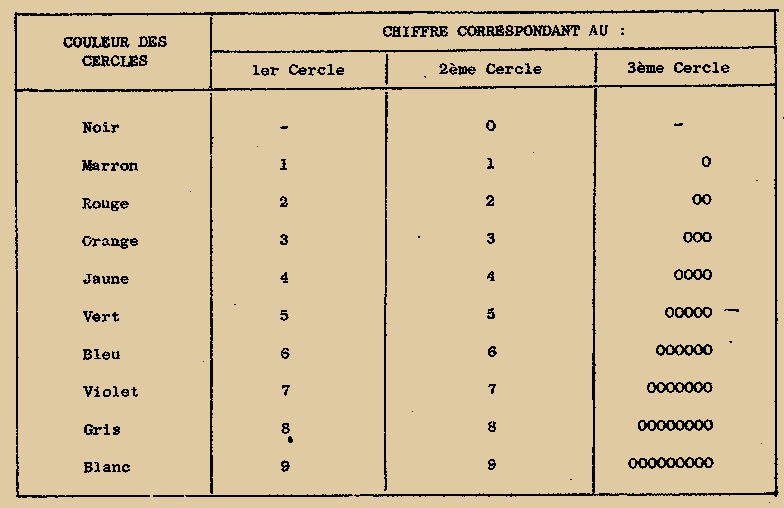
Fig. 3
MESURE PAR LA MÉTHODE DE DÉVIATION
La méthode de déviation utilise le plus souvent le principe de l’OHMÈTRE À PILE (Fig. 4).
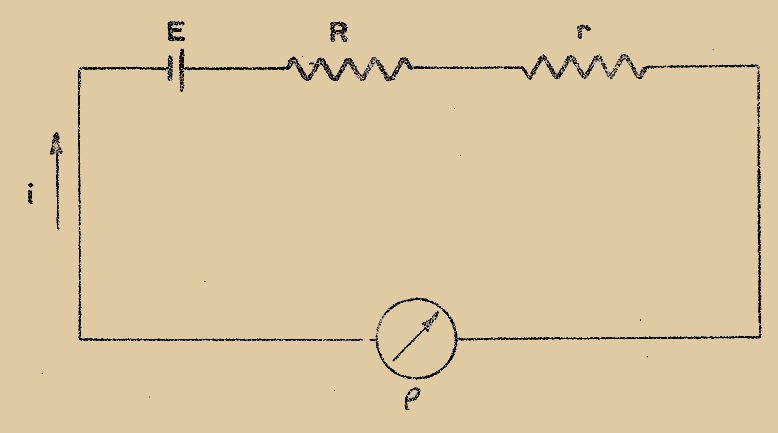
Fig. 4
Une source de force électromotrice "E" et de résistance "R" bien déterminée alimente en série le microampèremètre de résistance "ρ" et la résistance inconnue "r".
En appliquant la loi d’Ohm, on peut écrire :
"i" étant le courant circulant dans le montage.
Si la résistance "r" est nulle, c’est-à-dire si elle n‘existe pas, on observe un courant "i0" donné par :
De la première relation, on tire :
ou encore :
En remplaçant "R + ρ" par sa valeur tirée de la seconde équation, soit "R + ρ = E/i0 ", on peut écrire :
soit :
Si l’on connait parfaitement bien la valeur de la tension "E" de la pile et qu’on la suppose stable durant la mesure, on voit que la détermination de "r" ne dépend que des valeurs de "i" et "i0" lues sur le microampèremètre : l’ohmmètre à pile ne peut donc être qu’un appareil de contrôle sommaire.
Nous pouvons également citer une autre méthode faisant usage simultané d’un voltmètre et d’un ampèremètre (Fig. 5) :
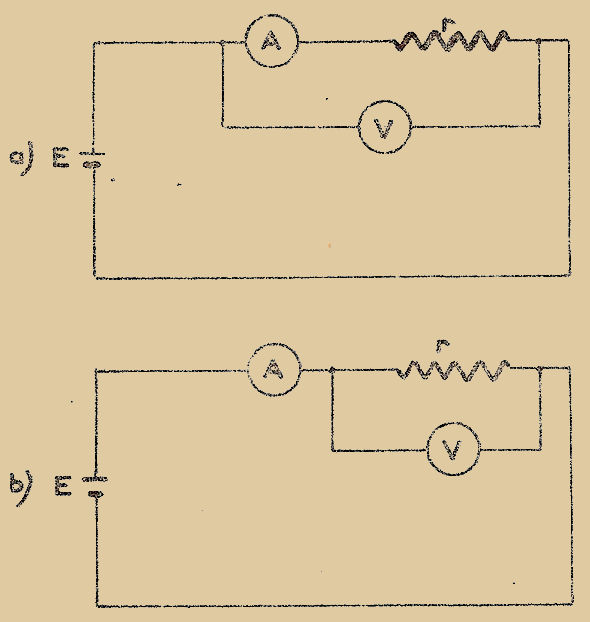
Fig. 5
a - Avec montage AMONT dans lequel le voltmètre mesure la chute de tension dans la résistance augmentée de la chute de tension dans l’ampèremètre ; on devra lors du calcul "U/I" ne pas omettre la résistance de l’ampèremètre qui se trouve en série avec la résistance inconnue.
b - Avec montage AVAL dans lequel l’ampèremètre mesure le courant traversant la résistance, courant MAJORÉ de la consommation du voltmètre ; ce montage convient particulièrement bien pour la mesure de résistances faibles par rapport à celle du voltmètre.
MESURE PAR LA MÉTHODE DE ZÉRO
Il s’agit ici essentiellement du montage EN PONT DE WHEATSTONE reproduit sur la Fig. 6.
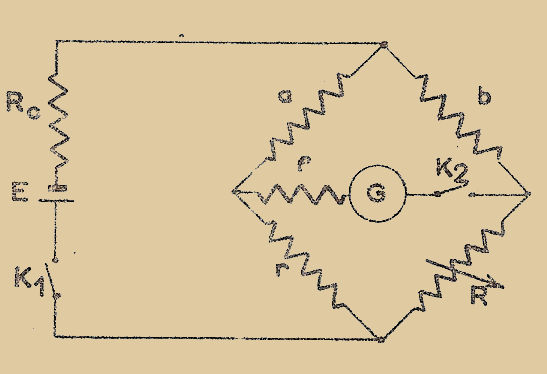
Fig. 6
On sait qu’à l’équilibre, c’est-à-dire lorsqu’aucun courant ne circule dans le galvanomètre "G", on détermine la valeur de la résistance "r" à mesurer par la relation :
indépendante de la position des diagonales pile et galvanomètre ; les résistances "a" et "b" forment la "tête de pont" : le rapport "a/b" a par construction une valeur égale à un nombre entier de 10 afin de simplifier les calculs.
La résistance R est une résistance variable étalonnée ; les clés "K1" et "K2" servent à couper les diagonales, et la mesure est indépendante des résistances "Rc" de la pile et "ρ" du galvanomètre (plus la sensibilité de ce dernier est grande, plus la précision du montage est bonne).
MESURE PAR LA MÉTHODE D’OPPOSITION
Si le montage en pont de Wheatstone est le plus souvent utilisé ; il ne convient pas toujours, en particulier s’il s’agit de mesurer des résistances de faible valeur. En effet, il devient alors peu précis de se baser sur un rapport "a/b" de deux résistances différentes (Fig. 6) qui peuvent varier de façon appréciable surtout si elles sont parcourues par des courants importants : ce qui sera le cas si la résistance "r" est très faible, car on ne peut pas trop affaiblir le courant par l’emploi de résistances "a" et "b" élevées sans aller au détriment de la précision de la mesure.
On a alors recours à un montage dans lequel la résistance "a", dite de mesure, est une fraction de potentiomètre étalonné de faible valeur.
Examinons la Fig. 7 où "r" est la résistance inconnue et "R" une résistance fixe de valeur connue, "ρ" étant une résistance variable destinée à limiter le courant dans le potentiomètre.
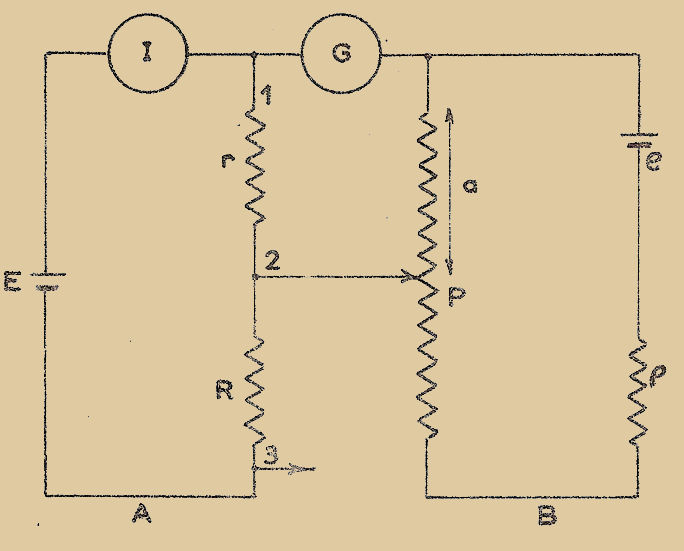
Fig. 7
- On oppose successivement les chutes de tension aux bornes de "r" et "R" dans le circuit "A" à la chute de tension dans une fraction "a" du potentiomètre "P" du circuit "B" à travers le galvanomètre "G".
- Soit "I" le courant circulant dans l’ampèremètre.
Lorsque le circuit "A" est connecté au circuit "B" par ses bornes 1 et 2 et que le curseur du potentiomètre "P" a été réglé pour que le galvanomètre n’indique aucun courant, on peut écrire que le courant "I" est donné par :
la chute de tension aux bornes de "r" est donc :
De même on a dans le circuit "B", un courant "i" à travers "P" :
et une chute de tension aux bornes de "a" :
Puisque "G" indique un courant nul, on peut écrire :
Connectons maintenant le circuit "A" au circuit "B" par ses bornes 2 et 3 ("G" se trouve alors sur la branche 3) : pour obtenir un nouvel équilibre, il faudra déplacer le curseur de "P" sur une nouvelle position ; soit "b" la nouvelle valeur de la fraction de "P", on peut écrire :
En divisant membre à membre 1) et 2), on peut écrire :
ou encore :
Cette méthode d’opposition est la plus courante lors de la mesure de résistances de très faibles valeurs ; il suffit comme on le voit de disposer d’un potentiomètre étalonné de faible valeur.
MESURE PAR LA MÉTHODE DE L’OHMMÈTRE ÉLECTRONIQUE
>Le voltmètre électronique se prête particulièrement bien à la mesure de résistances de fortes valeurs, par le fait même que l’impédance d’entrée est forcément élevée.
Le schéma de principe est donné Fig. 8.
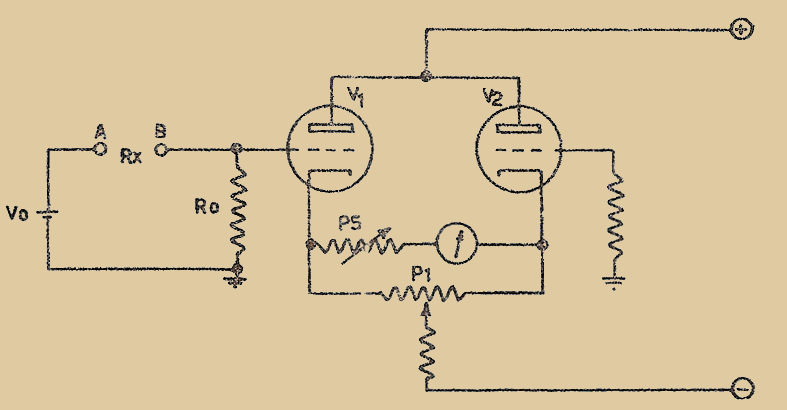
Fig. 8
"Rx" est la résistance inconnue, "R0" une résistance de très grande valeur assurant la polarisation de "V1", "P5" le potentiomètre d’équilibre : le microampèremètre placé en série indique le déséquilibre lorsque la résistance "Rx", de valeur infinie en circuit ouvert, est insérée dans le circuit de mesure.
Le montage de l’Ohmmètre électronique est abondamment étudié dans les leçons théoriques de ce cours : nous ne l’avons ici mentionné que pour mémoire.
LA MESURE DES CAPACITÉS
CHARGE ET DÉCHARGE D’UN CONDENSATEUR
La 10ème leçon de Métrologie a vu l’analyse des différents types de condensateurs : étudions maintenant le processus de charge et décharge d’un condensateur.
Examinons la Fig. 1a ; supposons que nous fermions "S" : la tension CONTINUE "V" se trouve appliquée aux armatures du condensateur et celui-ci se CHARGE, ce qui signifie que les charges positives fournies par la pile parcourent le conducteur et atteignent l’armature supérieure de "C".
Autant il y a de charges positives arrivant sur l’armature supérieure, autant de charges positives situées sur l’armature inférieure sont repoussées et rejoignent le pôle – de la pile : un tel courant de charges "Ic" dure jusqu’à ce que le condensateur soit chargé c’est-à-dire jusqu’à ce qu’il ait emmagasiné une certaine quantité d’électricité ; au bout de ce temps, on devra trouver à ses bornes une différence de potentiel égale à la tension "V" de la pile
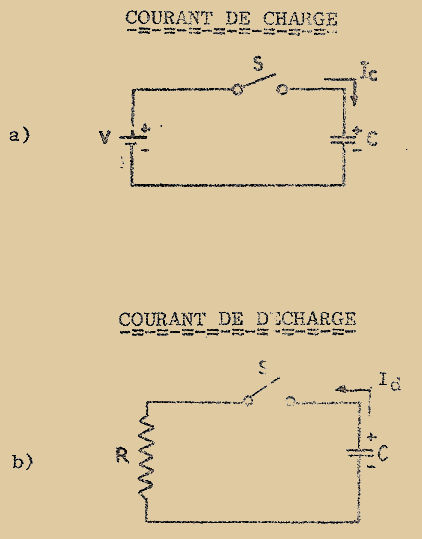
Fig. 1
La quantité d’électricité "Q" est liée à "C" et "V" par la relation :
En ouvrant "S", le condensateur reste chargé, si l’on fait abstraction du courant de fuite, et on a toujours "V" à ses bornes.
Refermons maintenant le condensateur sur une résistance "R" (Fig. 1b) : en abaissant "S", le condensateur se déchargera dans le circuit et il y a circulation d’un courant de DÉCHARGE "Id" ayant une direction OPPOSÉE à celle qu’avait "Ic".
Examinons maintenant ce qui advient lorsque dans le schéma de la Fig. 1a on remplace la source continue par une tension alternative sinusoïdale du type représenté à la Fig. 2.
- 1er quart de période : la tension croît de 0 à "+V" max. Le courant de charge "Ic" est positif (Fig. 3a).
- 2ème quart de période : la tension décroît de "+V" max à 0. Le courant de décharge "Id" est négatif (Fig. 3b).
- 3ème quart de période : la tension décroît de 0 à "-V" max. Le courant de charge "-Ic" est opposé à celui du 1er quart (Fig. 3c).
- 4ème quart de période : la tension croît de "-V" max à 0. Le courant de décharge "Id" est positif (Fig. 3d).
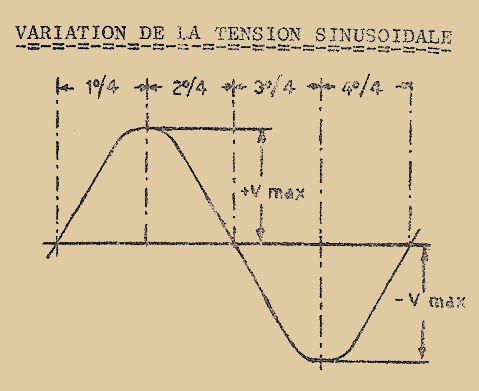
Fig. 2
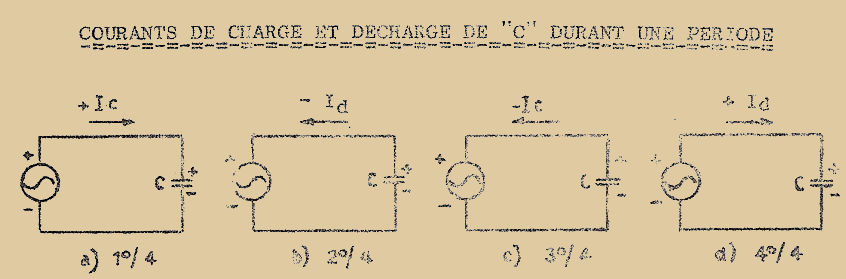
Fig. 3
La Fig. 4 représente la forme d’onde du courant comparée à celle de la tension : on vérifie que le maximum du courant a lieu un quart de période AVANT le maximum de tension ; on dira que le courant est DÉPHASÉ de 1/4 de période ((2.π)/4 ou 90°) en AVANCE sur la tension.
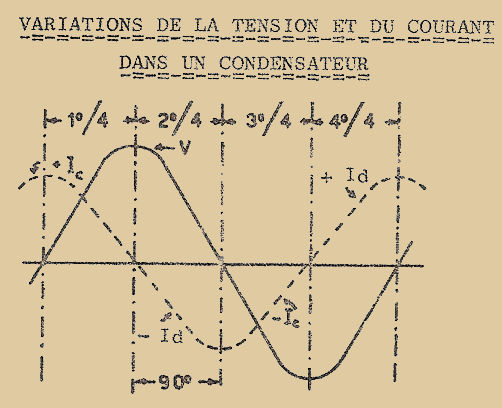
Fig. 4
RÉACTANCE D’UN CONDENSATEUR
Lorsqu’on branche aux bornes d’une résistance pure "R" une tension alternative "V", le courant de circulation est donné par :
Lorsqu’on branche la même tension "V" aux bornes d’une capacité "C" le courant "Ic" est donné par :
"Xc" s’exprime en ohms et est appelé la RÉACTANCE du condensateur ; on a d’autre part :
Ce qui permet de calculer la capacité "C", connaissant la fréquence "f" de la tension.
Toute mesure de capacité n’est donc théoriquement valable que pour une fréquence particulière de fonctionnement.
Rappelons qu’une résistance et une capacité en série constituent une impédance de valeur :
Une résistance et une capacité en parallèle constituent une impédance de valeur :
MÉTHODES DE MESURES DES CAPACITÉS
a – Méthode de déviation directe :
Cette méthode est surtout utilisée aux fréquences industrielles ; un type d’appareil à lecture directe, le CAPACIMÈTRE, est une transposition en courant alternatif du classique ohmmètre à pile. Le schéma de l’appareil se réduit à celui de la Fig. 5.
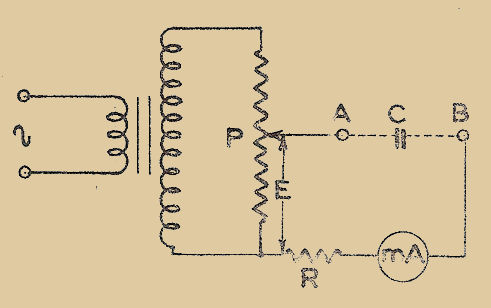
Fig. 5
Dans une première phase on court-circuite les bornes de branchement "A" et "B" et on règle la tension "E" au moyen du potentiomètre "P" pour que le milliampèremètre accuse la déviation maximum correspondant à une intensité déterminée "i0" :
Dans un deuxième temps, on branche la capacité "C" à mesurer, "Xc" étant la réactance de cette capacité, le courant diminue et devient :
Comme "E = R.i0", on peut écrire en remplaçant "Xc" par sa relation donnant "C" :
d’où :
Le milliampèremètre pourra être gradué directement en capacité, évidemment dans cette mesure il y aura lieu de connaître avec précision la valeur de la fréquence "f" :
b – Méthode du pont de SAUTY :
Le pont de Sauty est absolument l’analogue du pont de Wheastone en alternatif.
Il consiste à équilibrer le courant de circulation dans les branches du pont (Fig. 6) de telle façon qu’on puisse écrire :
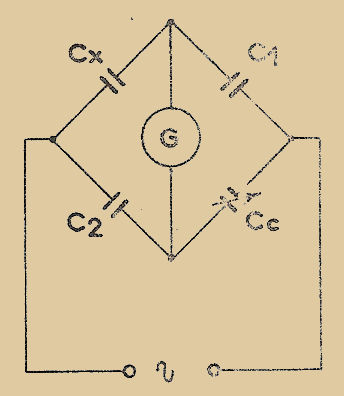
Fig. 6
ou ce qui revient au même :
"C1" et "C2" sont des capacités de valeurs fixes connues ; "Cc" est une capacité variable étalon.
CAPACIMÈTRE ÉLECTRONIQUE
Reprenons le schéma de la Fig. 5 où l’appareil de mesure de tension est un voltmètre électronique ; nous pouvons dans une première phase faire la mesure en court-circuitant "A" et "B" (c’est-à-dire sans capacité Cx, circuit fermé), le courant sera donné par :
Branchons maintenant la capacité "Cx" à mesurer et ajustons notre appareil pour que le courant de circulation "I" reste le même en le tarant par exemple en bout d’échelle ; on a alors :
On peut donc écrire :
d’où l’on tire facilement "Xc" puis "C", connaissant "V", "Vx" et "R".
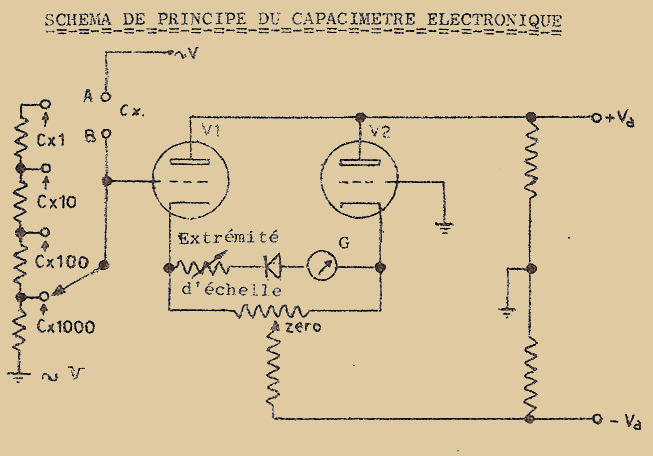
Fig. 7
Le schéma de principe d’un capacimètre électronique est donné à la Fig. 7 ; la diode en série avec le milliampèremètre "G" est nécessaire si ce dernier n’est valable qu’en "C.C."
ERREURS DE MESURE DUES AUX DÉFAUTS D’ISOLEMENT DES CONDENSATEURS
Le tarage de l’échelle d’un capacimètre est fait en tenant compte de la seule réactance de "Cx" qu’on suppose être parfaitement isolé.
En fait on sait qu’un condensateur n’est jamais parfaitement isolé et qu’il existe toujours en parallèle une RÉSISTANCE DE FUITE "Rc" (Fig. 8).
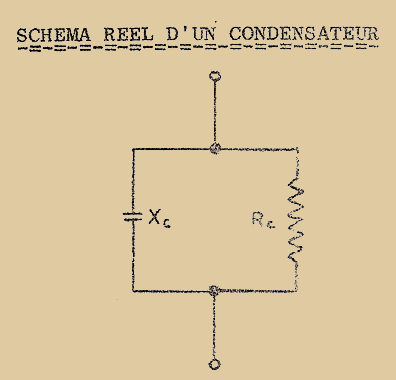
Fig. 8
L’impédance "Z" du condensateur est donc représentée par la relation :
Le courant de circulation est en fait la somme du courant qui traverse le condensateur (déphasé de 90° sur la tension à ses bornes) et du courant à travers la résistance "Rc" (en phase avec la tension : l’indication donnée par l’appareil aboutira à une valeur supérieure à la valeur vraie.
Le diagramme de la Fig. 9 indique la valeur minimum que doit présenter la résistance de fuite d’un condensateur pour que la mesure au capacimètre électronique ne soit pas entachée d’une erreur de plus de 5%.
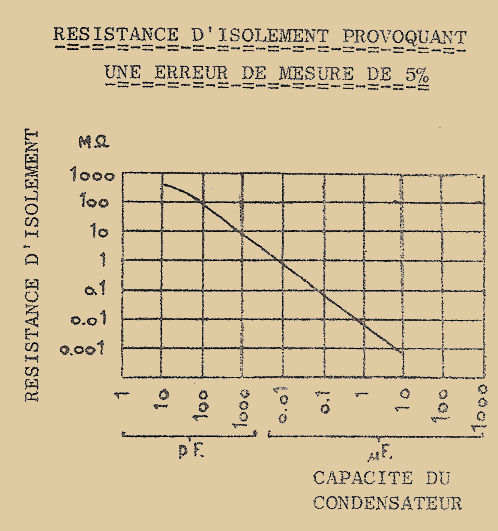
Fig. 9
Il sera donc toujours prudent avant de procéder à la mesure d’une capacité de contrôler sa résistance de fuite et de vérifier qu’elle n’est pas inférieure à une certaine limite.
LA MESURE DES INDUCTANCES
La mesure des inductances est très proche de celle des capacités quand on a pris soin d’exprimer l’un ou l’autre de ces éléments par sa réactance.
La réactance dite INDUCTIVE d’une inductance est donnée par :
où "L" est la valeur de self induction proportionnelle en particulier au nombre de spires de la bobine.
Une inductance présente rarement une réactance pure (de même que les capacités comme nous l’avons vu précédemment), mais on peut néanmoins réaliser des éléments qui sont très voisins, dans un domaine de fréquence plus ou moins étendu, de réactance pures : il faut alors faire état d’une nouvelle notion qui est la surtension.
COEFFICIENT DE SURTENTION :
Cette notion de surtension caractérise l’approximation avec laquelle on peut précisément considérer une réactance comme étant pure. On appelle coefficient de surtension "K" à la fréquence "f" d’une impédance le rapport entre la tension développée aux bornes de cette réactance par un courant de fréquence "f" et la tension que développerait ce même courant aux bornes de la partie active de cette impédance :
pour une capacité : K = √(R2 + Xc2)/R = √(R2 + 1/(ω2.C2))/R
pour une inductance : K = √(R2 + XL2)/R = √(R2 + ω2.L2)/R
Le COEFFICIENT DE QUALITÉ d’une impédance est défini par :
Ce coefficient est le rapport des tensions développées par un courant de fréquence "f" respectivement aux bornes de la partie réactive ("ωL", s’il s’agit d’une inductance) et de la partie active (résistance pure "R") de l’impédance.
À la RÉSONANCE, l’impédance de charge devient :
puisque dans un circuit accordé sur la fréquence de résonnance, on a L.C.ω2 = 1
On voit tout de suite qu’on a la relation :
On exprime parfois l’inverse du coefficient de qualité par la tangente de l’ANGLE DE PERTE de l’impédance :
Si l’impédance est pure, "K" et "Q" sont infinis, puisque "R" est considéré comme nul ; réciproquement 1/Q caractérise la perfection d’un élément voisin d’être une résistance pure.
Q-MÈTRE ET SELFMÈTRE :
Q-mètre et Selfmètre sont deux appareils permettant la mesure comme leurs noms l’indiquent du coefficient de qualité et du coefficient de self induction par la méthode DE RÉSONANCE.
Le principe de la mesure est schématisé à la Fig. 1 où "V" désigne un voltmètre d’impédance d’entrée infinie (voltmètre électronique).
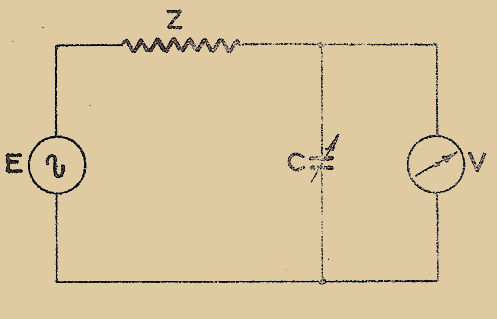
Fig. 1
L’impédance "Z" inconnue supposée inductive est branchée en série dans le circuit alimenté par une source "E" connue ; on règle alors le condensateur variable "C" de manière à ce que le voltmètre "V" indique une déviation maximum (résonnance) : on peut écrire que la chute de tension "E" qui se produit dans le circuit est développée dans la partie ACTIVE de l’impédance.
d’où :
"E" étant connu, le voltmètre "V" peut être gradué directement en coefficient de qualité : cet appareil est un Q-mètre.
Le Selfmètre est un Q-mètre simplifié comprenant un oscillateur à fréquences préréglées modulé en amplitude, chacune des fréquences correspondant à une gamme de mesures, et un condensateur variable directement gradué en inductance.
L’observation de la résonnance se fait à l’aide d’un voltmètre à haute impédance et d’un haut-parleur fonctionnant sur le courant détecté par le voltmètre.
MÉTHODE DU PONT DE MAXWELL :
La Fig. 2 représente un circuit classique de mesure d’une inductance par comparaison avec une capacité variable étalon "C".
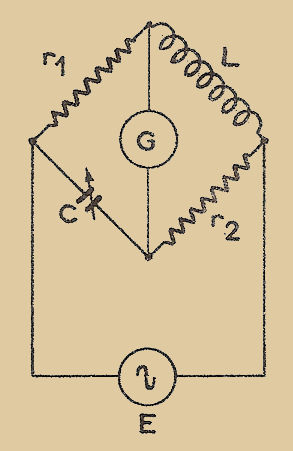
Fig. 2
À l’équilibre, constaté par le galvanomètre "G", on peut écrire :
où :
d’où l’on tire :
On voit que l’équilibre est indépendant de la fréquence pourvu que la valeur de la capacité soit connue aux différentes fréquences auxquelles on désire effectuer la mesure.
LA MESURE DES FRÉQUENCES
La mesure des fréquences et des temps occupe dans l’ensemble des opérations de mesures électriques et électroniques une place particulière qui relève d’une technique très générale, la CHRONOMÉTRIE.
FRÉQUENCE ET PÉRIODE :
Un phénomène est dit PÉRIODIQUE si son amplitude "A" varie au cours du temps de manière telle que l’on peut définir une durée "T" (ou période) telle que l’amplitude au bout du temps "t + T" soit égale à celle qu’elle avait au temps "t" :
quelle que soit l’époque "t" considérée.
La quantité f = 1/T est la fréquence du phénomène qui s’exprime en Hertz si "T" est en secondes.
Quand le phénomène est purement sinusoïdal on peut poser avec l’origine des temps choisie convenablement :
avec ω = (2.π)/T = 2.𝜋.f
ω : pulsation du phénomène sinusoïdal s’exprimant en radians par seconde.
Voyons par exemple la représentation d’une onde sinusoïdale Fig. 3 où l’axe des ordonnées représente l’amplitude "A" de la tension et l’axe des abscisses le temps "t" : la durée Od est la période "T" du phénomène
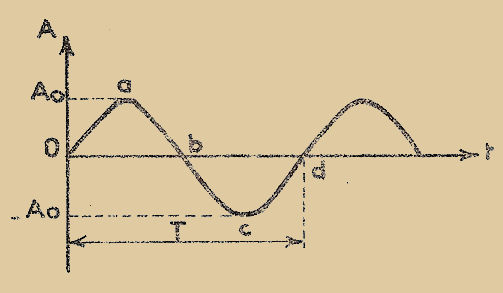
Fig. 3
On a bien successivement :
- au point 0 : t = 0 et A = A0.sin(0) = 0
- au point a : t = T/4 et A = A0.sin(π/2) = A0
- au point b : t = T/2 et A = A0.sin(𝜋) = 0
- au point c : t = 3.T/4 et A = A0.sin(3.π/2) = - A0
- au point d : t = T et A = A0.sin(2.𝜋) = 0
Par cette représentation on voit qu’on pourra mesurer la fréquence en comptant par des procédés dits de chronométrie électronique le nombre de périodes contenues dans un intervalle de temps connu.
L’étude des FRÉQUENCEMÈTRES a été abondamment analysée dans la 2ème partie de ce Cours de Mesures : nous rappellerons le principe du fréquencemètre hétérodyne utilisant le principe des battements, et décrirons brièvement une méthode de mesure en pont souvent utilisée en pratique.
FRÉQUENCEMÈTRE HÉTÉRODYNE :
Lorsque la fréquence à mesurer et une fréquence étalonnée variable excitent toutes deux un écouteur téléphonique, un opérateur comparant ces fréquences par écoute simultanée perçoit une sensation de BATTEMENTS dont il peut distinguer par exemple 0,1Hz pour une fréquence de l’ordre de 1.000Hz : la comparaison peut être effectuée à 10-4 près.
Le principe consiste à moduler la fréquence à mesurer par une fréquence étalonnée issue d’un oscillateur local : ce dernier est un oscillateur à réaction à accord continu réglable par condensateur à air ; il est généralement étalonné à l’aide d’un oscillateur à quartz.
Le couplage entre le fréquencemètre et la source est toujours très faible de façon à réduire les risques d’entraînement de fréquence de la source : l’appareil doit être toujours soigneusement blindé.
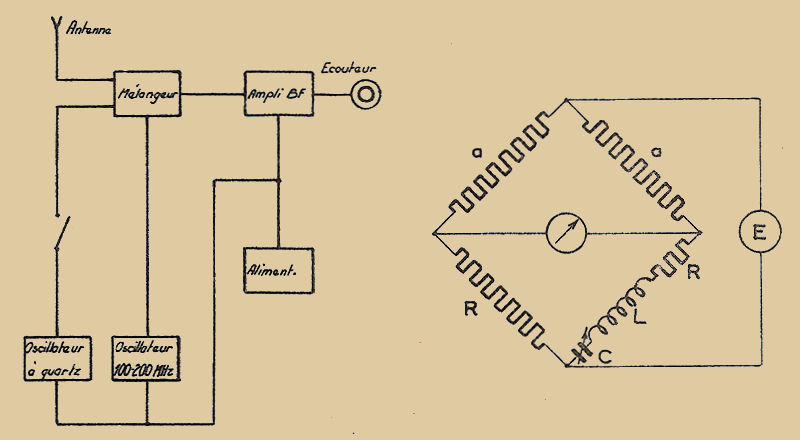
Fig. 4 et 5
La précision relative que l’on peut atteindre dans une mesure de fréquence est 10-5, elle est généralement de 10-4. La Fig. 4 donne le schéma d’un fréquencemètre à précision de 10-4, comportant un oscillateur à quartz sur 5MHz.
PONT À RÉSONANCE :
On sait qu’un circuit "LC" accordé à la résonance présente une fréquence caractéristique :
Le montage de la Fig. 5 représente un pont de mesure accordé à la résonance au moyen de la capacité variable étalonnée.
Un inconvénient vient de ce que l’inductance n’est pas toujours bien connue, en particulier la part de la résistance pure.
Par ailleurs, la capacité variant comme le carré de la fréquence introduit des erreurs non négligeables : pour toutes ces raisons on préfère le montage suivant.
PONT DE ROBINSON :
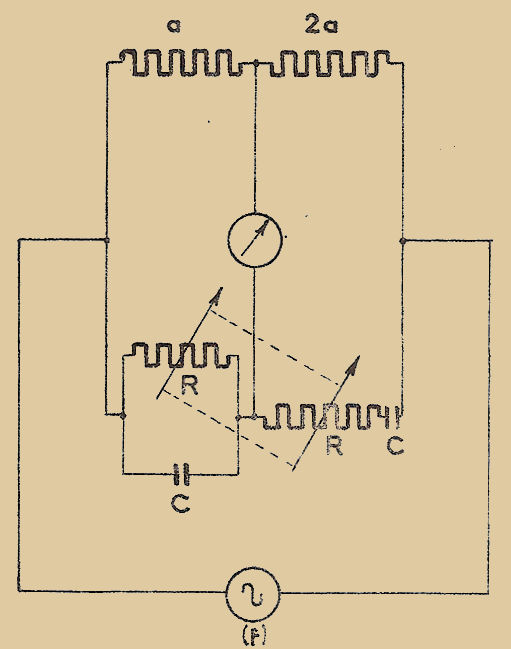
Fig. 6
Le pont de Robinson est le montage le plus employé dans la pratique : le schéma en est donné à la Fig. 6.
Les résistances "a" sont des résistances parfaitement égales ; les résistances "R" sont des résistances variables simultanément ; les condensateurs "C" sont des condensateurs fixes étalonnés de précision.
À l’équilibre on peut écrire :
et par transformations successives :
On démontre (résolution de l’équation du second degré) que la seule solution possible de l’équation est :
Soit :
Le calcul de la fréquence s’opère donc très aisément : on démontre par ailleurs que l’influence des facteurs de perte des condensateurs (angle de perte) n’est pas très important, ce qui rend ce montage un des plus utilisés dans la pratique courante des mesures de fréquences.
MESURES EN RÉGIME IMPULSIF
Les signaux, tels que la voix ou la musique, sont transmis par modulation de l’onde porteuse. Dans sa forme la plus simple, la porteuse est une onde continue à fréquence fixe, dont l’amplitude est modulée suivant les fluctuations du signal.
La modulation d’amplitude a ceci de caractéristique que l’onde modulée peut-être transmise dans une bande de fréquence très étroite.
D’autres formes, comme la modulation de fréquence et la modulation d’impulsions, requièrent des BANDES DE FRÉQUENCES PLUS LARGES, mais elles offrent en contre partie des avantages qui justifient cette largeur de bande.
SIGNAUX IMPULSIFS
Dans les circuits d’impulsions, ce qui intéresse est moins la fréquence fondamentale de l’onde et de ses harmoniques que la FORME de l’onde et ses variations de l’entrée jusqu’à la sortie du circuit.
Le signal fondamental est le SIGNAL CARRÉ (Fig. 1a) pour lequel la tension passe brutalement d’un niveau constant à un autre niveau ; les flancs sont alors raides et le sommet plat.
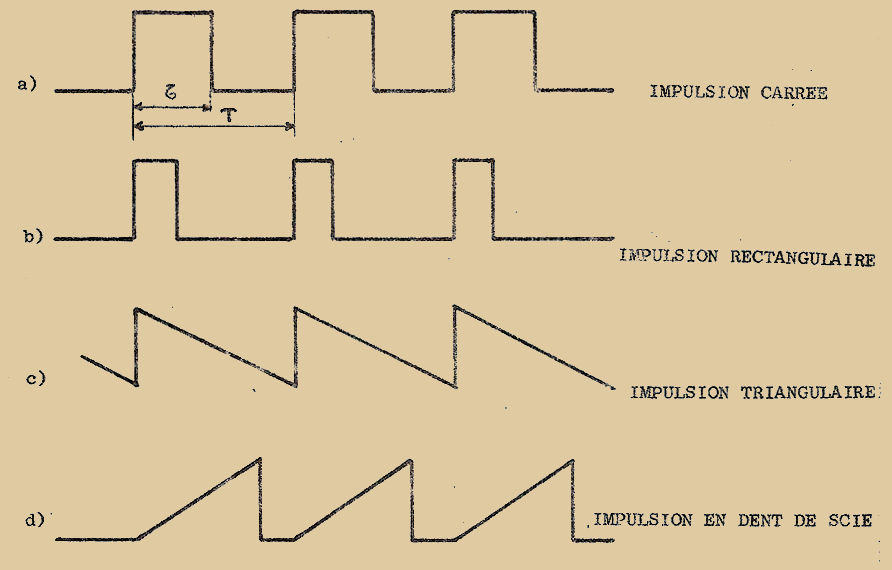
Fig. 1
Il est alors défini par une amplitude V, une durée τ et une période de répétition T, intervalle de temps entre les flancs de montée de deux impulsions successives : pour un signal carré τ = T/2.
Un signal dit RECTANGULAIRE présente toujours des flancs raides et un sommet plat, mais la durée n’est plus égale à la période (Fig. 1b). Dans la plupart des cas cependant les impulsions ne sont pas aussi régulières mais ont lieu seules ou à intervalles réguliers.
Une autre forme d’impulsion est l’impulsion TRIANGULAIRE (Fig. 1c et 1d), ou signal en DENT DE SCIE, ou encore BASE DE TEMPS de l’OSCILLOGRAPHE CATHODIQUE : lorsqu’une telle impulsion est appliquée aux plaques de déviation horizontale d’un oscillographe, son spot balayera l’écran à un rythme uniforme et revient à une vitesse admise comme infinie pour recommencer le mouvement.
L’oscillographe est donc l’appareil qui permettra d’étudier la forme de tout autre signal qui serait appliqué aux plaques de déviation verticale.
Les signaux carrés et triangulaires ont un grand nombre d’HARMONIQUES : les circuits qui le véhiculent doivent donc fonctionner dans une bande de fréquence très large si on désire qu’ils soient transmis fidèlement.
L’atténuation des hautes fréquences donne lieu à un arrondissement des flancs ; celle des basses fréquences produit une distorsion du niveau de base et détruit la linéarité de la dent de scie. Nous ne reviendrons pas ici sur les différentes méthodes de production des signaux à caractère impulsif (univibrateur, transitron, etc…) abondamment décrits dans les Leçons Théoriques 23 et 24 : examinons ici les problèmes posés par les mesures de tels signaux.
MODULATION D’IMPULSIONS
Les différentes méthodes de modulation d’impulsions sont au nombre de trois et sont représentées à la Fig. 2. La modulation en HAUTEUR (a) correspond à la modulation d’amplitude d’une onde continue.
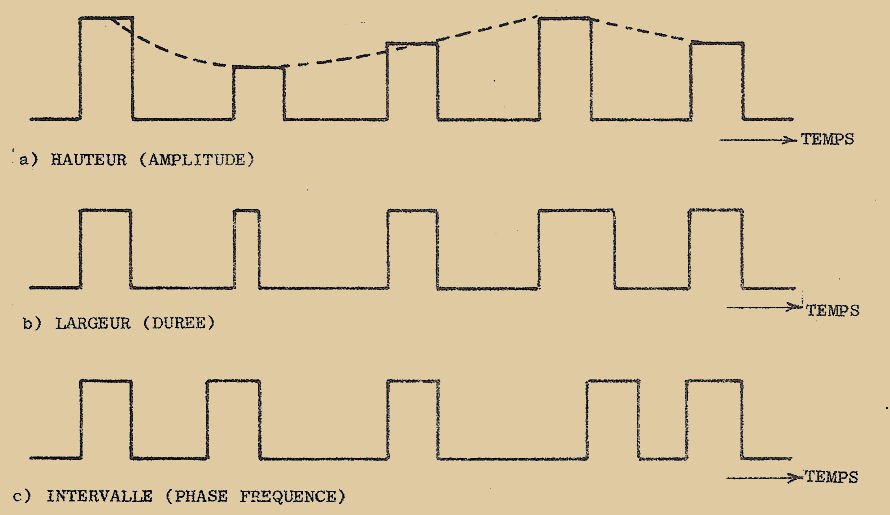
Fig. 2
La modulation en LARGEUR ou DURÉE (b), de même que la modulation en INTERVALLE (c), se réfèrent essentiellement à une notion de temps et en conséquence ne réagissent nullement sur l’amplitude de l’impulsion qui reste constante.
Les avantages les plus marquants se trouvent dans les modulations du type b ou c : l’amplitude n’ayant pas à être une fonction de mesure, le système de détection utilisé reste indifférent aux fluctuations d’amplitude en particulier à celles qui ont pour origine l’instabilité des sources d’alimentation ; les mesures se ramènent dans ces cas-là à des mesures de TEMPS.
Les circuits à échos d’impulsions, tels que le radar, sont basés sur une mesure d’intervalle, c’est-à-dire de temps, pour déterminer la distance de l’obstacle.
D’autres types d’informations, tels que les signaux correspondant à des nombres, peuvent être transmis par association combinée d’une série d’impulsions : chaque série sera évaluée par un compteur d’impulsions qui calculera en outre les durées et les intervalles. Ici encore il s’agit de mesure de temps.
Nous avons dit plus haut que la modulation d’impulsions nécessiterait des largeurs de bandes suffisantes : en effet il ne pourra être procédé à des mesures de temps que si les impulsions ne subissent aucune déformation due à une fréquence de coupure trop basse des circuits de détection.
Dans la plupart des chaînes de transmission, par exemple en M.F., on admet que la largeur de bande minimum des circuits de détection doit être au moins le double de la bande de fréquence propre à l’impulsion (celle-ci est donnée par le rapport f(Hz) = 1/τ , où τ est la durée de l’impulsion exprimée en seconde).
Si l’impulsion a une fréquence f, le circuit devra présenter une largeur de bande au moins égale à 2 f, autour de f0, fréquence de transmission (Fig. 3).
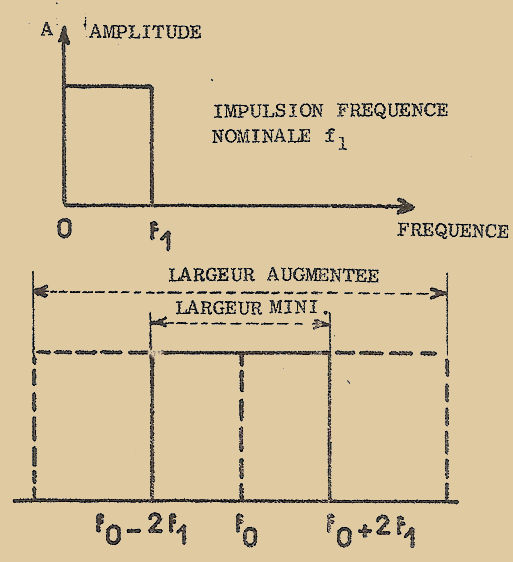
Fig. 3
Cependant plus la largeur de bande est grande, meilleure est la sélectivité des impulsions et moins déformées sont ces dernières, ce qui assure une mesure plus exacte.
La Fig. 4 montre les distorsions que subit une impulsion à l’origine parfaitement carrée lorsqu’on la détecte après passage dans un circuit dont la largeur de bande est variable.
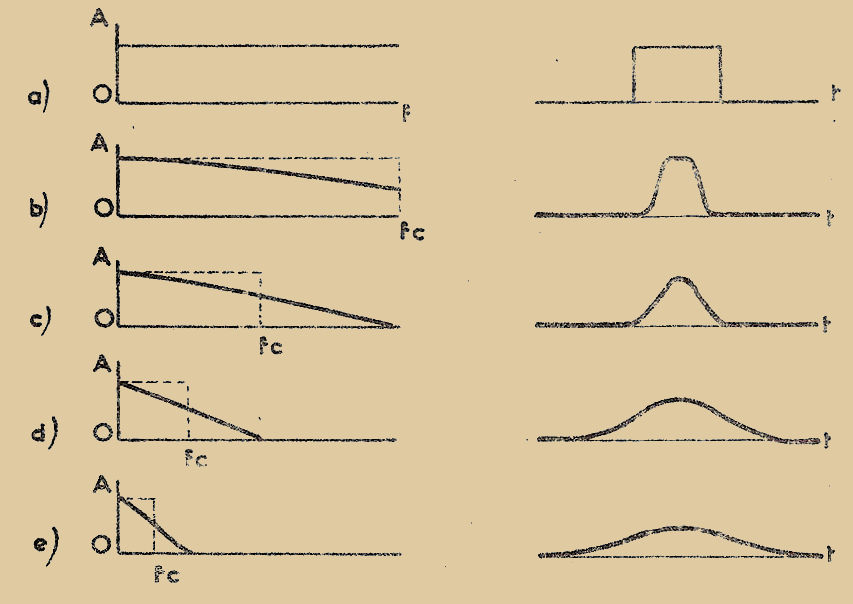
Fig. 4
- en a) : l’impulsion carrée représente l’impulsion de tension ou de courant produite par un système à très grande largeur de bande.
- en b) : la largeur de bande fc du circuit est quatre fois la largeur de bande nominale de l’impulsion ; on constate que les flancs sont arrondis, mais le sommet reste plat.
- en c) : la largeur de bande fc est deux fois la largeur de bande nominale de l’impulsion ; le sommet est nettement arrondi.
- en d) : la largeur de bande fc est égale à la largeur de bande nominale de l’impulsion, celle-ci est déjà aplatie et nettement élargie.
- en e) : la largeur de bande fc n’est plus que la moitié de la largeur de bande nominale ; l’impulsion est considérablement écrasée.
MESURE DES AMPLITUDES
Une impulsion classique de courant ou de tension observée sur un oscilloscope se mesure convenablement si le scope est calibré comme le montre la Fig. 5. Les traits fins qui sont des impulsions appelées PIPS sont des marqueurs superposés apparaissant à des intervalles caractéristiques donnant une échelle des temps.

Fig. 5
Sur les oscilloscopes de très bonne précision, utilisés dans les mesures d’impulsions, chaque pip est séparé du voisin par une durée d’une microseconde et tous les 5 pips le marqueur est plus grand.
La Fig. 5 représente une impulsion dont la largeur au sommet est de une division , et la largeur à la base environ deux microsecondes ; à mi-amplitude, sa largeur est d’à peu près 1,5 µS.
Dans le cas où il s’agit d’une impulsion contenant plusieurs cycles de la porteuse, si l’oscilloscope ne dispose pas de circuit de balayage à la fréquence exacte de la porteuse il y aura difficulté à mesurer l’impulsion : l’onde porteuse devra alors être redressée avec les déformations que cela risque d’entraîner pour l’impulsion à moins toutefois que le redresseur ait un temps de réponse suffisamment court.
Une autre méthode utilisée lorsque le scope n’est plus calibré en amplitude consiste à se servir de la valeur de la puissance moyenne : le rapport entre la puissance crête et la puissance moyenne est égal au rapport entre la période de répétition de l’impulsion et la durée propre de l’impulsion ; notons que la période de répétition (qui est une durée) est l’inverse de la fréquence de répétition, cette dernière exprimant le nombre d’impulsions qui se succèdent dans l’unité de temps.
La puissance crête est alors exprimée par le rapport : puissance moyenne x (période de répétition)/(durée de l impulsion)
Cette méthode n’est convenable que si la durée de l’impulsion est très faible par rapport à la période de répétition du phénomène.
La puissance moyenne se mesure au moyen d’un dispositif thermique comme le thermocouple, et la durée d’impulsion s’observe sur l’oscilloscope.
MESURE DES DURÉES ET SPECTRE DE FRÉQUENCE
La méthode la plus simple pour mesurer la durée d’une impulsion est celle de la Fig. 5.
Il existe cependant une autre méthode basée sur l’observation du SPECTRE DE FRÉQUENCE de l’impulsion (Fig. 6).
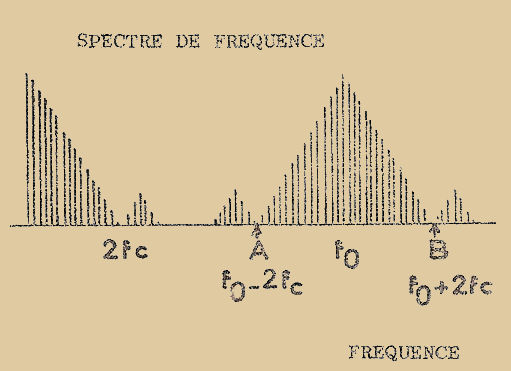
Fig. 6
Le spectre de fréquence d’une impulsion a une largeur inversement proportionnelle à la largeur de l’impulsion ou durée de l’impulsion ; de plus s’il s’agit d’une impulsion à flancs raides, le spectre présente une valeur minimum à une fréquence différant du maximum de 2 fc : les fréquences de ces réponses minima peuvent être détectées par un récepteur à accord "pointu".
En déplaçant le détecteur entre les points A et B, on détermine par lecture sur le cadran d’un ondemètre, les valeurs f0 – 2 fc et f0 + 2 fc, et donc fc ; la durée de l’impulsion sera donnée par la relation :
Une impulsion simple, ou une onde pulsée, a un spectre de fréquence qui se présente comme à la Fig. 6 : s’il s’agit d’une impulsion son spectre sera centré sur la fréquence zéro ; s’il s’agit d’une onde pulsée, le spectre sera centré sur la fréquence de la porteuse.
Il ne peut y avoir de spectre valable que si le circuit est capable de sélecter une largeur de bande bien inférieure à celle du spectre lui-même ; pour faire apparaître le spectre de fréquence sur l’écran d’un oscilloscope on utilise un appareil spécial dit ANALYSEUR DE SPECTRE : l’impulsion est appliquée au récepteur et la sortie redressée apparaît par action des plaques de déflexion verticales.
Les impulsions apparaissent alors comme des lignes verticales dont les hauteurs respectives représentent l’amplitude relative du spectre de fréquence (Fig. 6).
VALEURS MOYENNES
Une impulsion qui se répète a une valeur moyenne de puissance, de tension ou de courant bien définie. L’un de ces éléments peut se déterminer par procédé calorimétrique dans un circuit ou un tube : lorsqu’il s’agit de tension et de courant, il faut encore préciser lors de la mesure s’il s’agit des valeurs moyennes ou efficaces.
La puissance moyenne, ou encore les valeurs efficaces de courant ou de tension, peut se mesurer par un appareil thermique ayant un temps de réponse (inertie) bien supérieur à la période de répétition des impulsions ; la puissance crête elle, apparaît dans un temps beaucoup trop court pour permettre à des appareils de mesure de réagir correctement.
Les appareils de mesures thermiques d’emploi courant sont le THERMOCOUPLE, le BOLOMÈTRE, le PHOTOMÈTRE et la résistance CALORIMÉTRIQUE : de tels appareils sont capables de mesurer des puissances moyennes sur des impulsions de fréquence U.H.F. (ultra high frequency : très haute fréquence), 100MHz et au-delà.
Le bolomètre est en fait un pont C.C. possédant sur une des branches, une résistance très sensible à la température, cette résistance est soumise à la puissance impulsive : la découverte de la thermistance a rendu ces appareils d’une excellente sensibilité. On calibre le bolomètre par mesure à l’équilibre de puissances connues en faisant circuler dans la thermistance un courant continu de valeur déterminée.
La technique des Impulsions a pris ces dernières années un développement considérable tant dans les domaines de la navigation, de la détection aérienne, maritime ou même terrestre, que dans les mesures de haute précision et le calcul électronique.
Leurs applications ne cessent de s’étendre.
Le CODE par impulsions remplace les systèmes télégraphiques classiques à base de machines électromécaniques dont le temps de réponse est forcément lent : la technique des impulsions électroniques permet les transformations de signaux faibles et leur amplification sous toutes ses formes.
Le RADAR dont les études de base remontent juste avant la deuxième guerre mondiale utilise le principe de mesure de temps entre le départ d’une impulsion H.F. très courte rayonnée par un aérien directif et son retour (ou écho) après réflexion sur un obstacle : dans ce cas d’utilisation, la durée de l’impulsion peut être inférieure à 0,1 microseconde et la fréquence de répétition (inverse de la période) à plusieurs kilohertz.
Le circuit générateur d’impulsions triangulaires, ou circuit base de temps, est l’élément fondamental des circuits de TÉLÉVISION qui a pour rôle de fournir une tension variant progressivement et linéairement avec le temps et permet ainsi le balayage linéaire de l’image.
Pour toutes ces applications la mise au point des circuits générateurs d’impulsions et leur calibrage revient essentiellement à une mesure des temps aux durées très courtes : l’OSCILLOGRAPHE CATHODIQUE est l’appareil fondamental du technicien, aussi nécessaire pour lui que le voltmètre électronique ou le générateur.

