Numérisation des cours Alain PASQUET, Mise en page Pascal CHOUR - 2016 - 2018

LECON 1

INTRODUCTION

Jusqu’en 1948, le tube électronique était le seul composant doué de la merveilleuse propriété d’amplifier le courant électrique (c’est pour cette raison, qu’on l’appelle "élément ou composant ACTIF" pour bien le distinguer des autres composants dits "passifs" tels que résistances, condensateurs, etc…). Le tube électronique était donc la pièce maîtresse dans toutes les communications radio-électriques et dans l’électronique en général.

En 1948, deux savants américains des laboratoires de recherches de la Bell Telephone, John BARDEEN et Walter H. BRATTAIN, annoncent au monde entier la découverte d’un nouveau composant actif ayant des caractéristiques analogues à celles des tubes électroniques : ils lui donnent le nom de "TRANSISTOR". Expliquer dès maintenant la signification d’un tel mot serait prématuré : il suffit pour le moment de savoir qu’il dérive de 2 mots : "Transfert" et "Résistance".

On pourrait penser, vu la provenance de ce nom, qu’un tel dispositif n’a que peu de relations avec un tube électronique surtout si l’on songe à sa propriété fondamentale, qui est l’amplification d’un courant électronique.

Bien que dans les 2 cas, le phénomène d’amplification soit obtenu par contrôle de l’intensité d’un flux d’électrons, le mode de production d’un tel flux et son contrôle sont totalement différents.

Il suffit pour cela de se rappeler que dans le cas des tubes, le milieu dans lequel se propage le flux électronique (courant anodique) est le vide existant dans l’ampoule qui forme l’enveloppe extérieure du tube, et que pour obtenir un tel flux, on doit porter la cathode à une forte température afin de déclencher le phénomène thermoïonique (ou émission thermique). Dans le cas des Transistors, par contre, le milieu dans lequel se déplacent les électrons est un solide, dont les propriétés peuvent être considérées comme intermédiaires entre celles des conducteurs et celles des isolants (d’où le nom de "semi-conducteur") ; pour obtenir le flux d’électrons (courant de collecteur, comme nous le verrons plus tard), nous n’avons pas besoin de chauffer une cathode, mais nous nous contenterons d’appliquer une tension continue aux électrodes du Transistor : de la même façon que l’on obtient un courant dans une résistance, lorsque l’on applique une tension à ses bornes.

Les analogies entre tubes et transistors s’arrêtent là : les phénomènes et les lois qui les régissent sont totalement différents.

Cette constatation amène une conclusion de caractère didactique extrêmement importante même si à première vue, elle parait, un non-sens ; la connaissance des tubes électroniques n’est pas un avantage dans l’étude des Transistors. Elle peut même devenir un inconvénient en ce sens que l’on cherche à faire naturellement des analogies entre tubes et transistors, analogies qui ne sont que superficielles et qui n’engendrent que des confusions.

L’étude des transistors devrait être complètement indépendante de l’étude des tubes électroniques et seules des comparaisons fort prudentes pourraient être avancées, et seulement lorsqu’il s’agit de passer d’un circuit composé de tubes, à un circuit à transistors ayant les MÊMES FONCTIONS. On dit d’ailleurs couramment, qu’un tel circuit est "Transistorisé".

Pour comprendre le fonctionnement des transistors, il est absolument indispensable de bien connaître, et de très près encore, les semi-conducteurs, en étudiant leurs propriétés physique et électriques. La compréhension de leur mode de fonctionnement ne peut être totale que si l’on s’est penché sur le monde de l’infiniment petit, c’est-à-dire sur le monde des atomes et des électrons.

L’étude des semi-conducteurs occupe un important chapitre de la science moderne : "la physique de l’état solide" dont les origines sont encore relativement anciennes. La première découverte sur les semi-conducteurs, c’est-à-dire sur la particularité de certaines substances à n’être ni des conducteurs ni des isolants, fut faite par FARADAY en 1833 (son nom est plus connu encore en Radio-électricité, et a servi à désigner l’unité de mesure de la capacité : le Farad).

FARADAY avait découvert en effet que le sulfure d’Argent présentait un coefficient de résistance négatif, ce qui signifie que sa résistance électrique diminue lorsqu’on le chauffe, contrairement à ce qui se passe pour les métaux dont la résistance augmente avec la température.

Quelque temps après, d’autres importantes propriétés des semi-conducteurs furent découvertes ; effet de REDRESSEMENT (c’est-à-dire propriété de laisser passer le courant plus facilement dans un sens que dans l’autre) ; PHOTOCONDUCTIVITÉ (c’est-à-dire propriété de présenter une résistance électrique différente selon la quantité de lumière reçue par la surface du semi-conducteur) ; PHOTO-ÉLECTRICITÉ (c’est-à-dire propriété de transformer l’énergie lumineuse en énergie électrique).

Les premières applications des semi-conducteurs furent faites à la fin du siècle dernier, après la découverte des ondes hertziennes et les expériences de MARCONI. On utilisait alors le carborundum et la galène (sulfure de plomb) pour la détection des ondes Radio.

Un autre pas en avant fut accompli après la première guerre mondiale, avec la production à l’échelle industrielle de redresseurs secs au sélénium (en 1920) et à l’oxyde de Cuivre (1926), encore très répandus de nos jours. Leur fabrication était alors faite de façon empirique, car on ne connaissait pas encore très bien les phénomènes de redressement de tels matériaux.

Les études sur les semi-conducteurs furent poursuivies toujours plus vigoureusement avec la découverte de nouveaux matériaux semi-conducteurs ; comme le silicium, et on remarqua que leurs propriétés de redressement s’amélioraient très nettement en utilisant des cristaux de silicium non parfaitement purs, mais contenant des quantités infimes d’impuretés. Pendant la seconde guerre mondiale, apparurent les diodes au silicium qui trouvèrent un champ d’application très vaste avec les fréquences extrêmement élevées (micro-ondes) utilisées dans les circuits Radars comme diodes de détection et comme mélangeuses.

La découverte du Transistor survint quelques années seulement après la fin de la seconde guerre mondiale en 1948.

Les savants BARDEEN et BRATTAIN effectuaient des expériences très poussées pour vérifier expérimentalement la présence de charges électriques à la surface d’un cristal semi-conducteur, comme la théorie le laissait prévoir.

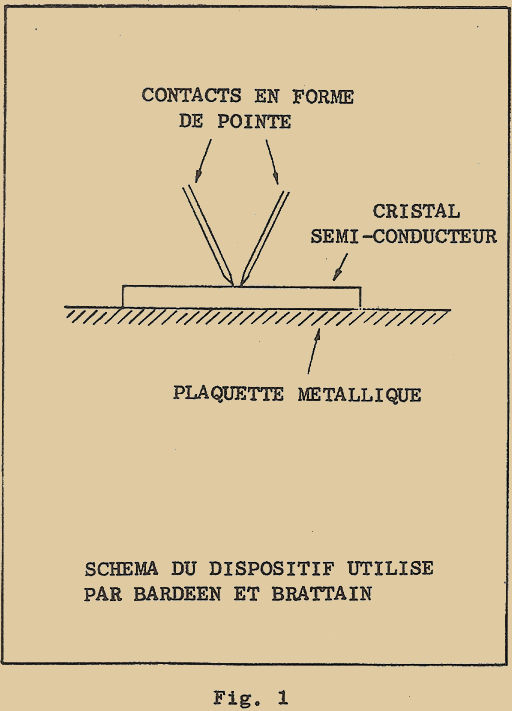
A cette fin, ils avaient disposé sur une plaquette métallique un cristal semi-conducteur. Sur ce cristal, ils avaient appuyé deux pointes métalliques de façon à former deux contacts en forme de pointe (figure 1). Pendant l’expérience, ils constatèrent un étrange phénomène : le courant qui se dirigeait d’une des pointes vers la plaquette métallique en traversant le cristal était "influencé" par le courant qui se dirigeait de la seconde pointe à la même plaquette : en d’autres termes, le courant d’une des deux pointes pouvait être COMMANDÉ par l’intermédiaire du courant de la seconde pointe.

Le phénomène était donc comparable à celui qui se manifeste dans les tubes électroniques, dans lesquels le COURANT entre 2 électrodes (cathode et plaque) est commandé en agissant sur la TENSION appliquée sur une 3^ème électrode (grille). Tout ceci laissait supposer que le dispositif avait la propriété, tout comme les tubes, d’AMPLIFIER le courant électrique.

Amélioré et perfectionné, un tel dispositif a constitué le premier type de transistor dit "à pointes", qui n’a pas bénéficié d’une très grande diffusion, à cause de deux défauts principaux : l’extrême petitesse des contacts à pointes limitait la puissance à des valeurs extrêmement faibles ; l’instabilité des contacts, rendait les caractéristiques des transistors très variables dans le temps, et ceux-ci étaient en outre générateurs de bruit.

En dépit de cela, la découverte du transistor "à pointes" a marqué d’une pierre blanche les progrès de l’électronique, et les études poursuivies pour expliquer le phénomène ont conduit le savant William SHOCKLEY (de la Bell Telephone) à présenter en 1951, un nouveau type de Transistor ayant des caractéristiques améliorées par rapport au Transistor à pointes : on l’appellera plus tard : "Transistor à Jonction".

Il faut souligner le fait que W. SHOCKLEY a découvert et étudié les caractéristiques du transistor à jonction par une voie purement théorique : ce n’est seulement que 3 ans plus tard, en 1954, que grâce au succès de W.G. PFANN à obtenir du germanium suffisamment pur, il a pu réaliser le premier transistor à jonction et démontrer expérimentalement les prévisions théoriques de sa découverte.

Après une certaine période d’essais expérimentaux, le Transistor apparut sur le marché et commença à concurrencer le tube électronique.

Les premiers transistors commerciaux étaient prévus pour la basse fréquence et pour les puissances relativement faibles. Leur utilisation était limitée à des amplificateurs BF., et aux premiers récepteurs radio appelés "hybrides" car ils comportaient des tubes pour les étages haute fréquence et moyenne fréquence et des transistors pour les étages BF.

Au fur et à mesure que la technique de fabrication s’améliorait, on fabriqua des transistors pour des fréquences de plus en plus élevées, et les récepteurs radio se "transistorisèrent" de jour en jour : non seulement, les tubes furent totalement éliminés, mais on commença à recevoir les ondes moyennes, puis courtes, pour arriver bientôt aux ondes ultra-courtes de la modulation de fréquence.

Les avantages des transistors par rapport aux tubes sont nombreux : en premier lieu, les dimensions des transistors sont notablement plus faibles que celles des tubes, même pour les tubes du type miniature. A la figure 2, je vous donne la comparaison avec un tube miniature de puissance (120 mW environ).

En second lieu, comme je vous l’ai déjà dit, le transistor ne nécessite aucune énergie de chauffage, et par conséquent consomme bien moins qu’un tube, lequel exige selon son type, et ceci uniquement pour le chauffage, une puissance de 1 à 3 W.

De plus, la tension de collecteur (qui correspond à la tension plaque) est souvent au maximum de 12V. Les appareils transistorisés peuvent donc fonctionner facilement avec une pile à basse tension, et qui de plus a une longue durée du fait de la faible consommation de courant.

Par constitution, le transistor est plus simple et plus robuste qu’un tube, étant donné qu’il est formé par une minuscule plaquette de cristal de germanium sur laquelle sont soudés 3 fils de connexions. Sa résistance aux chocs est beaucoup plus grande et sa vie pratiquement illimitée car il n’y a pas épuisement avec la durée d’utilisation comme c’est le cas pour les cathodes des tubes.

Par contre, il présente quelques inconvénients parmi lesquels les plus importants sont les suivants. Les transistors sont relativement fragiles du point de vue électrique : il suffit d’une surtension ou d’un courant anormalement élevé dû par exemple à un court-circuit accidentel pour le détruire définitivement. Leurs caractéristiques varient beaucoup avec la température et on ne peut les utiliser sans précautions particulières à des températures élevées (température maximum 70° C).

Les transistors d’un même type peuvent présenter des caractéristiques électriques assez différentes : d’ailleurs dans certains cas, comme par exemple pour un push-pull BF final, le fabricant donne des transistors apairés dont les caractéristiques sont très voisines.

Ce dernier inconvénient est assez important, surtout lorsque l’on doit procéder au remplacement d’un transistor détérioré. Dans quelques cas critiques, on pourra être amené à devoir trier le transistor désiré parmi plusieurs autres du même type.

Malgré tous ces inconvénients, les transistors ont trouvé de larges applications qui leur font progressivement remplacer les tubes électroniques dans tous les cas où il y a un problème de place, de poids, de consommation de courant.

Voici deux exemples différents : les amplificateurs pour surdité qui se trouvent placés dans un volume très réduit derrière l’oreille ; les circuits électroniques complexes placés dans les fusées télécommandées et les satellites artificiels.

Il ne faut pas cependant déborder d’un optimisme exagéré et affirmer que dans un avenir très proche les tubes électroniques vont disparaître. Bien que la technique des transistors aille rapidement de l’avant et se perfectionne de jour en jour, tubes et transistors sont de constitutions tellement différentes que ces derniers ne peuvent pas concurrencer les tubes dans certains domaines, et il y aura obligatoirement coexistence des deux.

Dans ce cours, l’étude des transistors sera subdivisée en 3 parties distinctes que nous intitulerons comme suit :

• NOTIONS SUR LA STRUCTURE DE LA MATIÈRE : c’est un chapitre relativement bref, réduit à l’indispensable pour bien comprendre le fonctionnement des transistors, et servant à l’introduction du chapitre suivant.
• PHYSIQUE DU TRANSISTOR, SES CARACTÉRISTIQUES ET SES PROPRIÉTÉS : description des différents types de transistors et quelques notions technologiques sur leur fabrication.
• CIRCUITS A TRANSISTORS : c’est le chapitre le plus important du Cours. Dans cette partie, je vous décrirai les différents circuits les plus couramment utilisés en technique Radio, tant du point de vue physique, pour une bonne et rapide compréhension de leur fonctionnement, que du point de vue calculs, donnant ainsi à ceux d’entre vous qui sont intéressés par la réalisation de circuits à transistors toutes les formules et méthode utiles.

INTRODUCTION

1 – CONSTITUTION DE LA MATIÈRE

1 - 1 MOLÉCULES ET ATOMES

Un des problèmes qui de tous temps a le plus préoccupé l’esprit de l’homme, est celui de la constitution de la Matière, c’est-à-dire "savoir de quoi étaient formées les différentes substances".

L’hypothèse que la matière pouvait n’être formée que de quelques éléments simples fut avancée par les philosophes grecs de l’Antiquité : ceux-ci pensaient que l’on pouvait obtenir les différentes substances en mélangeant seulement, en quantités appropriées, quatre éléments simples comme : l’AIR, la TERRE et le FEU.

Au 5^ème siècle avant Jésus Christ, un autre philosophe grec, Democrite, en partant de telles hypothèses de base, établit pour la première fois, une théorie "atomique" sur la constitution de la matière qui peut être considérée, sous ses différents aspects, comme l’embryon de la théorie atomique moderne. En se basant exclusivement sur des considérations philosophiques, Democrite concevait la matière comme formée de particules élémentaires qui ne pouvaient plus être divisées en d’autres particules plus petites ; c’est pour cette raison, qu’il leur a donné le nom "d’atomes", ce qui en grec signifie "indivisible".

Ces particules, toujours selon DEMOCRITE, étaient dotées d’un mouvement continuel et de leur rencontre accidentelle dépendait l’origine des substances, tandis que leur séparation en signifiait la destruction.

Les particules étant assemblées, laissaient cependant entr’elles des "distances" ce qui faisait que la matière était "pleine de trous". Mais les dimensions des atomes étant tellement petites, l’œil humain ne pouvait les distinguer, et la matière apparaissait solide et compacte.

DEMOCRITE n’avait aucune idée exacte sur les dimensions des atomes, et il ne précisait pas non plus de quelle espèce ils étaient faits. Mais il considérait les atomes comme indestructibles et affirmait que la matière ne pouvait être ni créée, ni détruite, mais seulement transformée. Ce principe fut fondamental pour les physiciens et les chimistes, et ce n’est seulement que ces derniers temps qu’il fut modifié grâce à la théorie de la relativité d’EINSTEIN, qui démontra la possibilité de transformer la matière en énergie (de telles transformations sont aujourd’hui courantes dans les centrales atomiques) et inversement.

Ce n’est qu’en 1808 que le chimiste anglais John DALTON en se basant sur les lois des combinaisons chimiques d’alors, élabora une nouvelle théorie atomique, qui grâce à sa clarté et à l’évidence des données expérimentales sur lesquelles elle se basait, fut immédiatement adoptée par tous les chimistes de l’époque. En se basant sur les constatations expérimentales selon lesquelles un corps composé était formé de quantités bien déterminées d’éléments simples. il devenait évident que ces corps composés devaient être formés de tant de particules élémentaires qui se combinaient les unes aux autres. Par exemple, l’expérience montrait que si l’on mélangeait 1 gramme d’hydrogène à 5 grammes d’azote, on obtenait 6 grammes d’ammoniac. On en déduisait qu’un atome d’ammoniac devait être composé d’un atome d’hydrogène et d’un atome d’azote et que ce dernier devait avoir un poids 5 fois plus grand que celui de l’hydrogène.

DALTON définit ainsi 2 types d’atomes : LES ATOMES SIMPLES, ceux des substances élémentaires, ou éléments, comme par exemple, l’hydrogène, l’azote, l’oxygène, le soufre, le fer, le zinc, le cuivre, le mercure, etc… ; LES ATOMES COMPOSÉS, ceux des substances composées, comme l’ammoniac, l’eau, l’acide nitrique, etc… Chacun des atomes peut être caractérisé par un numéro que DALTON appela "poids de composition", et qui exprime de combien de fois le poids d’un atome considéré est plus grand que celui de l’hydrogène, élément le plus léger de tous ; ainsi, le poids de composition de l’hydrogène était 1, celui de l’azote de 5, etc…

La même année où DALTON publiait sa théorie atomique, un chimiste français GAY-LUSSAC, énonçait une nouvelle loi sur la combinaison chimique des substances gazeuses. En considérant les volumes des gaz (naturellement, les gaz doivent être pris à la même température et à la même pression, sinon on ne peut plus parler de volume) ainsi que leurs poids, comme l’avait fait DALTON, GAY-LUSSAC découvrit que les volumes des gaz simples, qui se combinent pour donner lieu à un gaz composé, sont toujours dans un rapport simple : comme 1 à 1, 1 à 2, ou 1 à 3. Par exemple, dans le cas de l’ammoniac, on trouve que l’on doit combiner 1 volume (par exemple 1 litre) d’azote avec 3 volumes (par exemples 3 litres) d’hydrogène pour trouver 2 volumes (ou 2 litres) d’ammoniac (remarquez que l’ammoniac est un gaz qui, dissous dans de l’eau, donne un liquide appelé couramment ammoniaque). Un autre exemple est celui de l’eau : 1 litre d’oxygène combiné à 2 litres d’hydrogène donne lieu à 2 litres de vapeur d’eau.

Les expériences de GAY-LUSSAC confirment la théorie atomique de la matière : en effet si, dans la composition de l’ammoniac, on part de 1 litre d’azote et de 4 litres d’hydrogène, au lieu de 3, on remarque que l’on obtient encore 2 litres d’ammoniac et 1 litre d’hydrogène, ce qui signifie que le litre d’hydrogène mis en supplément, n’a pas pu se combiner. Ceci indique donc que l’ammoniac n’est pas un simple mélange de 2 gaz pris à peu près dans la proportion de 1 à 3, mais un véritable composé dans lequel les composants sont en proportions parfaitement définies, et ce ne peut être que si l’on admet que les gaz composants sont formés de "particules", et que chaque particule d’un gaz se combine avec un certain nombre de "particules" d’un autre gaz. Nous verrons tout à l’heure, ce que nous entendons par "particule".

Pour expliquer les résultats de GAY-LUSSAC, la théorie de DALTON se révèle insuffisante : en effet, elle ne peut expliquer pourquoi une particule d’une certaine substance ne peut se combiner qu’avec une seule ou avec plusieurs particules d’une autre substance.

Une explication complète a été avancée en 1811 par le chimiste italien AVOGADRO, qui a fait les remarques suivantes : pour une MÊME PRESSION ; et à UNE MÊME TEMPÉRATURE, des volumes égaux d’un gaz quelconque doivent contenir toujours le même nombre de "particules" ; il n’est pas dit que de telles particules sont constituées par un seul atome, elles peuvent aussi être formées de plusieurs atomes.

En supposant alors, que les "particules" d’hydrogène et d’azote sont formées toutes les deux par 2 atomes, la formation de l’ammoniac s’explique facilement comme il est indiqué à la figure 3-a. Supposons que nous prenions 1 volume d’azote qui contient 10 particules ou molécules chacune formée par 2 atomes (représentées sur la figure par des triangles assemblés deux à deux) et 3 volumes d’hydrogène contenant 30 molécules chacune d’elles formées par 2 atomes (représentées sur la figure par des rectangles assemblés deux à deux) : on voit comment pendant la réaction chimique, chaque atome d’azote (triangles) se combine avec 3 atomes d’hydrogène (rectangles) pour former au total 20 molécules d’ammoniac, c’est-à-dire 2 volumes d’ammoniac, comme le montre l’expérience.

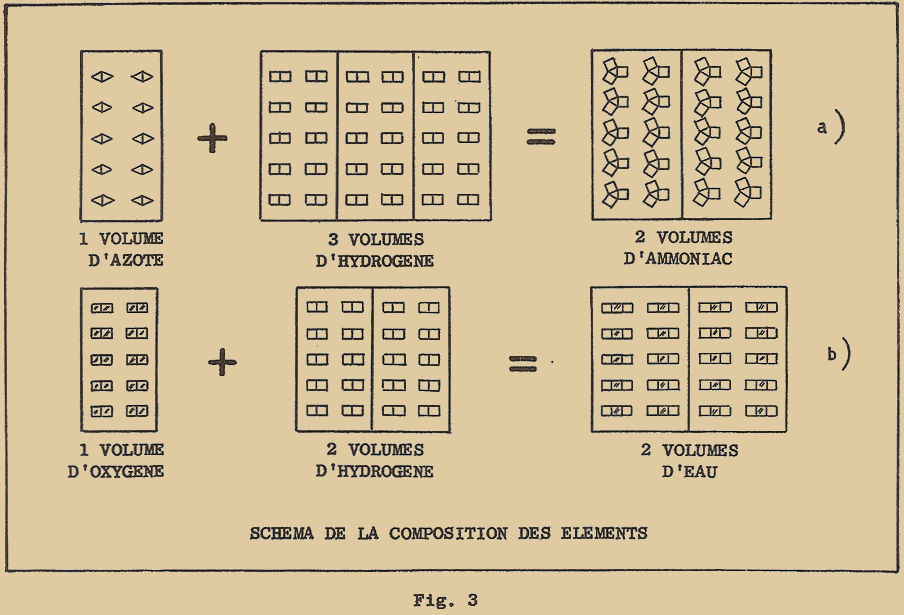
En raisonnant de la même manière, on peut représenter (figure 3-b), la réaction chimique entre 1 volume d’oxygène et 2 volumes d’hydrogène : elle donne lieu à 2 volumes d’eau (à l’état de vapeur).

Les hypothèses d’AVAGADRO ne furent pas acceptées aussi facilement, mais les expériences qui suivirent les confirmèrent toujours davantage et ceci même pour les substances non gazeuses. Aujourd’hui la théorie atomique de la matière s’appuie sur des bases solides et les notions des molécules et des atomes sont bien définies. Par MOLÉCULE on entend la plus petite partie d’un corps simple ou composé qui possède encore toutes les propriétés physiques et chimiques de ce corps. Par exemple, partons d’un grain de sel de cuisine (que l’on appelle en chimie chlorure de sodium) et divisons-le en 2 parties égales : nous obtenons 2 grains de sel plus petits, mais qui sont toujours du sel. Répétons l’opération en pensant que nous avons à notre disposition les appareils qui permettent d’effectuer un tel partage, autant de fois que nous le voulons (ceci d’ailleurs n’est pas possible en pratique, car les grains minuscules obtenus deviendraient trop petits). Il arrivera un moment, où il ne sera plus possible de partager le minuscule grain sans lui faire perdre sa propriété : ce minuscule grain représentera la molécule de chlorure de sodium. Si l’on divise une fois encore, on obtiendra un atome de chlore et un atome de sodium, c’est-à-dire les atomes des éléments qui constituent le chlorure de sodium et qui ont, chacun séparément, des propriétés différentes de celles de la substance qu’ils composent.

Si au lieu de considérer un corps composé, c’est-à-dire un composé chimique, on ne considère qu’un corps simple, soit un élément chimique réduit à la molécule, il sera encore possible de diviser cette molécule en 2 ou plusieurs atomes d’un même élément, si la molécule est poly-atomique (ainsi la molécule d’oxygène est divisible en 2 atomes d’oxygène), ou bien elle n’est plus divisible quand elle est monoatomique, car elle est déjà l’atome de cet élément (ainsi, la molécule de cuivre, comme celle d’ailleurs de tous les métaux, est formée d’un seul atome de cuivre).

Les expériences de GAY-LUSSAC ont aussi permis de définir un autre concept des plus importants pour l’étude des combinaisons chimiques : la VALENCE d’un élément. Elle caractérise la faculté d’un élément à se combiner avec d’autres éléments et s’exprime par le nombre d’atomes d’hydrogène qui se combinent, ou peuvent se combiner, avec un atome de la substance considérée. Par exemple, nous avons vu que dans la formation de l’eau, chaque atome d’oxygène se combinait avec 2 atomes d’hydrogène : nous dirons donc que l’oxygène a pour "valence 2" ou ce qui veut dire la même chose, qu’il est "bivalent". Dans le cas de l’ammoniac, chaque atome d’azote se combine avec 3 atomes d’hydrogène, ce qui signifie que l’azote a pour "valence 3", ou bien qu’il est "trivalent". Dans l’acide chlorhydrique on trouve qu’un atome de chlore se combine avec un seul atome d’hydrogène ; on dira donc que la valence du chlore est 1, c’est-à-dire qu’il est "monovalent" ainsi d’ailleurs que l’hydrogène.

Si au contraire on considère le cuivre, qui ne se compose pas avec l’hydrogène, on ne peut définir la valence de la même façon. Par contre, le cuivre se combine avec l’oxygène, pour former l’oxyde de cuivre utilisé dans les redresseurs et dans ce composé on trouve que chaque atome d’oxygène se combine avec 2 atomes de cuivre ; comme l’oxygène est bivalent, ceci signifie que chaque atome de cuivre a une seule valence.

Il existe des éléments qui ont une valence de 4 (tétravalent) comme le germanium et le silicium, et d’autres une valence 5 (pentavalent) comme l’arsenic ; on a rarement des valences supérieures. Il y a par contre 5 gaz (argon, hélium, krypton, néon, xénon) qui ne se combinent à aucun des éléments et que l’on appelle pour cette raison des gaz rares ou "nobles". Ils ont une valence nulle.

L’idée de valence présente un aspect différent à la lumière de la théorie électronique de l’atome ; elle est comme nous le verrons plus loin, de très grande importance pour comprendre les propriétés du germanium et du silicium.

1 – 2 CLASSIFICATION DES ÉLÉMENTS

Les nombreuses expériences poursuivies par les chimistes de l’Europe entière pour vérifier la théorie d’AVOGADRO, permirent de déterminer avec une très grande précision les "masses atomiques" des différents éléments.

"Masse atomique" ne signifie pas le poids en valeur absolue d’un atome, mais le poids relatif, c’est-à-dire de combien de fois l’atome d’un élément pèse plus que l’élément pris comme référence. Il était naturellement logique de prendre comme référence le poids de l’élément le plus léger, c’est-à-dire l’hydrogène, auquel on a donné par convention le poids atomique 1. De cette façon, il a semblé, d’après les premières expériences, que la masse atomique des différents éléments était toujours un nombre entier : ainsi, la masse atomique de l’hélium est 4, celle du carbone 12, celle de l’azote 14, celle de l’oxygène 16, et ainsi de suite ; des mesures plus précises ont permis de vérifier ultérieurement que ceci n’était pas tout à fait exact et que par exemple la masse atomique de l’oxygène était 15,88 et non pas 16.

On préfère actuellement, maintenir la valeur de 16 pour l’oxygène et s’en servir de référence pour les autres masses atomiques. Celles-ci sont alors légèrement différentes et on trouve : 1,008 pour l’hydrogène ; 4,003 pour l’hélium ; 12,01 pour le carbone ; 14,008 pour l’azote, etc…

La masse atomique a pris rapidement une importance très grande, car avec la valence, elle permet de calculer le rapport en poids des différents éléments d’une réaction chimique déterminée ; MASSE ATOMIQUE et VALENCE sont les nombres caractéristiques de chaque élément : ils en définissent les propriétés chimiques.

Au début du siècle, on connaissait 75 éléments, repérés chacun par 2 nombres qui correspondaient respectivement à la MASSE ATOMIQUE et à LA VALENCE. On a cherché ensuite à classer les éléments selon d’autres critères ; ainsi en 1817, l’allemand DOBEREINER chercha à regrouper les éléments 3 par 3, car il avait remarqué l’existence de "triades" d’éléments ayant des propriétés chimiques semblables, comme par exemple : le fer, le cobalt et le nickel ; le lithium, le sodium et le potassium ; le chlore, le brome et l’iode.

D’autres classifications furent faites en 1862 par le français CHAUCOURTOIS et en 1863 par l’anglais NEWLAND, mais celles-ci n’aboutirent à aucune conclusion définitive.

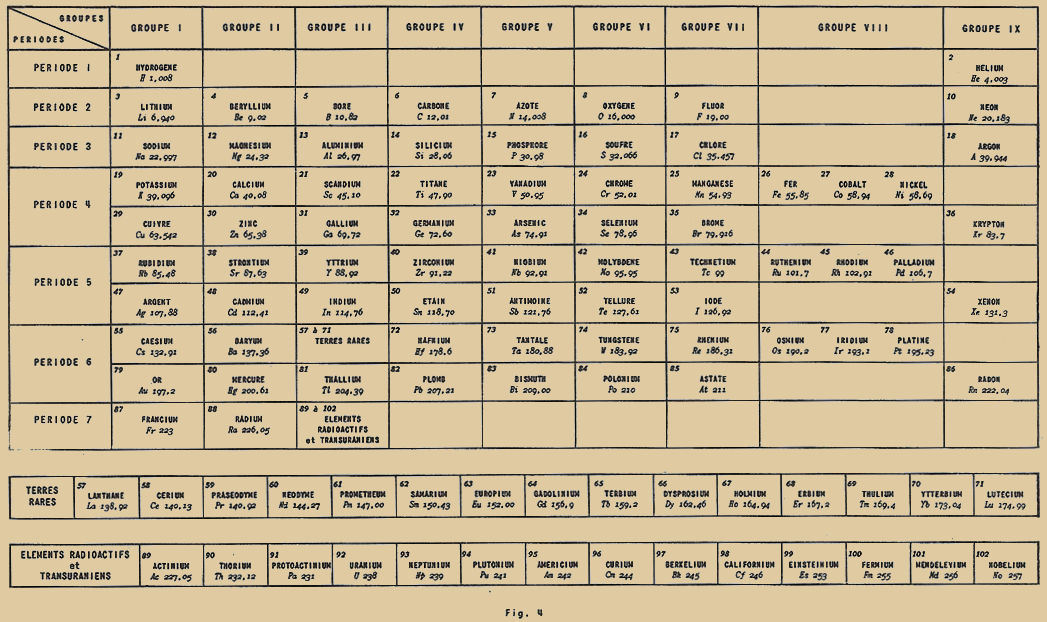
En 1868, le russe MENDELEÏEV fut plus heureux. Il améliora une classification faite par l’allemand MEYER. Les différents éléments furent classés selon un critère très simple, c’est-à-dire selon leur masse atomique, et de cette classification MENDELEÏEV tira des conclusions extrêmement intéressantes. Il remarqua que les principales propriétés des éléments se répétaient dans un certain ordre, à quelques rares exceptions. Ainsi, en plaçant les éléments sur une ligne horizontale selon leur masse atomique, on peut dresser un tableau de 9 colonnes, et dans chacune de celles-ci on place les éléments qui ont des propriétés physiques et chimiques semblables, en particulier ceux qui présentent la même valence. Ainsi fut créée la fameuse CLASSIFICATION PÉRIODIQUE DE MENDELEÏEV. A la figure 4, je vous donne un tableau complet rassemblant tous les éléments connus à ce jour.

Comme vous pouvez le voir, cette table est composée de 7 lignes, chacune d’entr’elles représentant une PÉRIODE, et de 9 colonnes, qui contiennent les groupes des éléments ayant des propriétés analogues. Dans chaque case, figurent un nombre, le nom de l’élément, son symbole (c’est-à-dire le sigle utilisé dans les formules chimiques) et enfin la masse atomique.

En regardant le tableau, on pourrait croire à première vue que le nom donné de "périodique" est impropre, en ce sens que les différentes lignes (ou périodes) ne sont pas égales. La première ligne est la plus simple car elle ne contient que 2 éléments seulement, l’hydrogène (H) et l’hélium (He), respectivement dans la première et dernière colonne. La seconde et la troisième, sont plus complètes, mais encore simples, car elles ne contiennent chacune que 8 éléments.

On remarquera que chaque période commence avec un élément monovalent et se termine par un élément de valence zéro : les éléments intermédiaires ont des valences qui croissent normalement jusqu’à 4 et puis de nouveau décroissent.

Ainsi les éléments de la seconde colonne sont BIVALENTS, ceux de la troisième TRIVALENTS, ceux de la 4^ème TETRAVALENTS (valence 4). A partir de là, la valence recommence à diminuer ; ainsi les éléments de la 5^ème colonne sont TRIVALENTS, ceux de la 6^ème BIVALENTS, ceux de la 7^ème MONOVALENTS, ceux de la 8^ème, sont des éléments particuliers pouvant avoir une ou deux valences secondaires, et enfin ceux de la dernière colonne, ont pour valence zéro.

Les 4^ème, 5^ème et 6^ème périodes sont plus complexes et peuvent être subdivisées chacune en 2 sous-périodes ; si l’on classe par ordre croissant de masse atomique, avant d’arriver aux éléments de valence zéro, on rencontre 2 séries d’éléments ayant des valences croissant d’abord de 1 à 4, puis décroissant de 4 à 1 ; mais entre ces deux séries d’éléments, on trouve trois éléments, de propriétés très semblables, qui ont été classés dans la 8^ème colonne.

Dans la 6^ème période, nous remarquons un cas particulier très intéressant : on a été obligé de placer sous la rubrique "Terres rares", une quinzaine d’éléments : ceux-ci en effet sont tellement semblables par leurs propriétés physiques et chimiques qu’il était difficile de les séparer. Ceci a donc justifié de les classer comme un seul élément, bien qu’en réalité chacun d’eux ait une masse atomique différente, comme on peut le constater en bas du tableau.

La dernière période comprend les éléments les plus lourds, parmi lesquels l’URANIUM et les éléments TRANSURANIENS découvert récemment.

Il faut encore remarquer que l’ordre croissant des éléments ne dépend pas rigoureusement de la masse atomique : il suffit d’observer le tableau pour voir qu’il n’y a pas continuité entre les éléments 18 et 19 (argon et potassium), 27 et 28 (cobalt et nickel), 52 et 53 (Tellure et l’Iode).

La composition de ce tableau par MENDELEÏEV ne fut pas aussi simple qu’elle peut apparaître maintenant, on doit de souvenir qu’à cette époque de très nombreux éléments étaient encore inconnus et le tableau se trouvait alors être incomplet.

L’habileté de Mendeleïev, fut de disposer les différents éléments connus de façon à ne pas interrompre la périodicité du tableau : de nombreuses cases furent laissées libres. On pouvait ainsi non seulement prévoir l’existence d’autres éléments qui restaient à découvrir, mais aussi prévoir leur caractéristiques (si l’on se basait sur l’existence d’une périodicité) de même que leur valence, leur masse atomique avec une certaine approximation, et leur propriétés chimiques.

Les éléments dont Mendeleïev avait prévu l’existence sont ceux des cases 21, 31 et 32 qui furent découverts (ou mieux : retrouvé et isolés des minéraux qui les contenaient), quelques années après. On leur donna le nom de la nation qui les découvrait : ainsi à l’élément 21 découvert par le chimiste suédois NILSON, on donna le nom de SCANDIUM (de Scandinavie) : à l’élément 31, découvert par le chimiste français LECOQ de BOISBAUDRAN, on donna le nom de GALLIUM (de la Gaule ancien nom de la France) et enfin à l’élément 32, découvert par l’allemand WINKLER, on donna le nom de GERMANIUM.

Au fur et à mesure que le tableau périodique se complétait de nouveaux éléments, la connaissance de la matière se précisait. De plus, on étudiait la matière en ses composants les plus petits et chaque particule était soigneusement classée selon ses caractéristiques puis affectée d’un numéro d’ordre. On peut donc dire que tous les "édifices" de la nature (c’est-à-dire tous les corps composés), peuvent être créés à l’aide d’un nombre limité de "briques" (les éléments) se composant entr’eux selon un ordre déterminé.

1 – 3 CONSTITUTION DE L’ATOME

Après la découverte des rayons X, des électrons et de la radioactivité, on se trouvait en présence de phénomènes qui ne pouvaient être expliqués à l’aide de la théorie atomique de la matière : de tels phénomènes ne pouvaient être expliqués que si l’on admettait l’existence de charges électriques, négatives et positives que ne prévoyait pas la théorie atomique. L’hypothèse suivant laquelle l’atome était la plus petite partie de la matière et ne pouvait plus être divisé, n’était plus valable.

En 1911, l’anglais Lord RUTHERFORD proposa le premier modèle composé d’un noyau formé d’un nombre de charges positives égale au numéro d’ordre de l’élément considéré : ces charges positives furent appelés PROTONS. Puisque l’atome à l’état naturel est électriquement neutre (ce qui signifie que chaque charge positive doit être compensée par une charge négative équivalente), RUTHERFORD compléta son modèle d’atome, en disposant tout autour, autant d’électrons qu’il y avait de protons dans le noyau.

L’expérience montra encore que les électrons étaient extrêmement légers, et que leur poids était une très faible part de celui de l’atome ; de ces considérations, on déduisit que le poids d’un atome dépendait presque exclusivement de celui de son noyau (c’est-à-dire des protons) : aujourd’hui, on sait qu’un proton pèse 1840 fois plus qu’un électron.

Nous pouvons maintenant essayer de représenter les différents types d’atomes. En commençant par l’hydrogène, qui est le premier dans la classification de MENDELEÏEV, nous dirons que son noyau est composé d’une seule charge positive (un seul proton) ; il n’y aura par conséquent qu’un seul électron autour de son noyau. Si nous passons au second élément, l’hélium, son noyau doit être composé de 2 protons et de 2 électrons : mais c’est là qu’apparut la première difficulté.

En effet, la masse atomique de l’hélium devrait être exactement double de celle de l’hydrogène, puisqu’il est formé de 2 protons et de 2 électrons. Or l’expérience était formelle et indiquait que l’hélium pesait 4 fois plus que l’hydrogène. Pour tourner la difficulté, on devait alors supposer que le noyau de l’hélium était composé de 4 protons, mais comme il devait avoir une charge positive égale à 2, deux des 4 protons devaient être intimement liés chacun à un électron, ce qui le rendait alors neutre.

Ce n’est qu’en 1932, que le physicien anglais JAMES CHANDWICK découvrit que le couple proton-électron, imaginé par RUTHERFORD n’était en réalité qu’une seule et unique particule, de poids égal à celui d’un électron et d’un proton, mais privée de charges électriques, c’est-à-dire qu’il était électriquement neutre ; c’est pour cette raison, qu’il lui donna le nom de NEUTRON.

Le modèle de l’atome fut encore modifié quelques années après, par le physicien danois NIELS BOHR. Se basant sur les résultats de longues et patientes recherches effectuées par l’anglais Henry MOSELEY – expériences qui consistaient à examiner un nombre considérable de métaux à l’aide des rayons X -, et se basant aussi sur les conclusions que les électrons ne devraient pas seulement tourner autour du noyau mais se déplacer sur des orbites bien déterminées, il proposa un modèle d’atome, très semblable à celui d’un système solaire miniature, où le soleil serait le noyau autour duquel tournaient les planètes (électrons).

Selon Bohr, il y avait seulement 7 orbites possibles, correspondant chacune à une des périodes de la table de Mendeleïev, et disposées à des distances croissantes du noyau. Ainsi les éléments de la première ligne (H et He, c’est-à-dire l’hydrogène et l’hélium) ont respectivement 1 et 2 électrons disposés sur la première orbite la plus voisine du noyau et repéré par la lettre K, cette orbite se trouve complète avec 2 électrons seulement.

Tous les éléments de la seconde ligne (du Li au Ne) ont deux électrons sur l’orbite K et les électrons restants (de 1 à 8) se trouvent sur une seconde orbite, appelée L et qui se trouve complétée avec 8 électrons au maximum. Le même phénomène est valable pour la 3^ème ligne. Celle-ci possède les orbites K et L complètes et une 3^ème orbite plus éloignée du noyau que les précédentes, appelée M ; qui n’a qu’un électron pour le premier élément (Na = sodium) et se trouve complétée à 8 électrons avec le dernier élément de la même ligne (Ar = Argon)

Pour les éléments des 3 groupes suivants, on ajoute 3 nouvelles orbites respectivement N, O et P ; celles-ci à leur tour sont divisées en 2 "sous-orbites" correspondant aux 2 lignes qui subdivisent ce groupe. Une 7^ème orbite Q intervient enfin pour les éléments du dernier groupe.

Bien que la théorie moderne ait un peu modifié la distribution des électrons sur les différentes orbites, le principe reste celui indiqué par BOHR. Je vous ai représenté à la figure 5 quelques exemples d’une telle représentation. On peut en tirer d’importantes conclusions qui permettent de voir d’une manière différente la signification de la notion de valence des éléments et d’expliquer l’aptitude des électrons à quitter plus ou moins facilement l’atome pour se combiner à d’autres éléments.

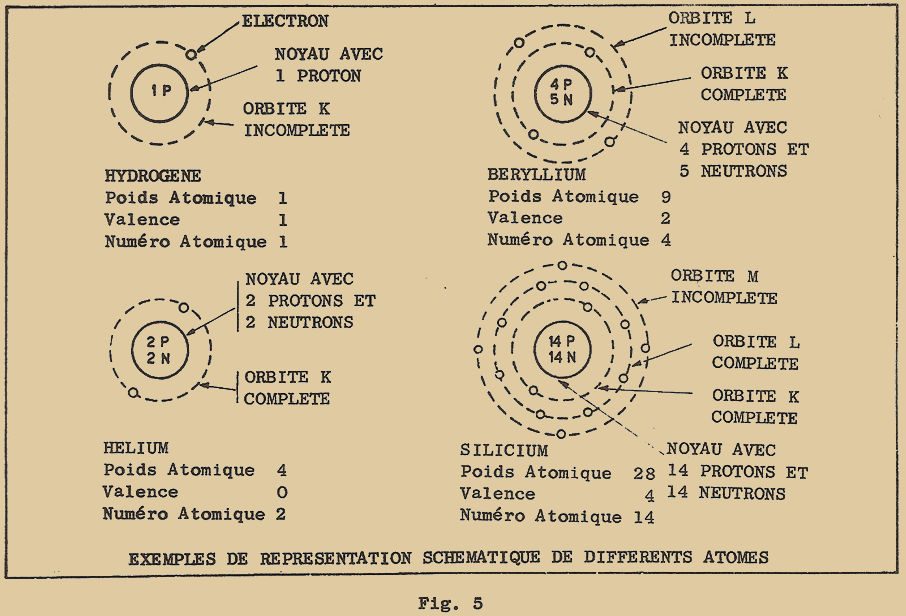
On peut remarquer encore que tous les atomes de la première colonne du tableau, qui sont monovalents comme nous l’avons vu, n’ont qu’un seul électron sur leur orbite la plus externe. Les atomes de la seconde colonne sont bivalents et possèdent au contraire deux électrons sur la même orbite externe : ceux de la troisième colonne sont trivalents et en comportent 3 ; ceux de la quatrième, 4. Les atomes de la dernière colonne ont une orbite externe complète avec 8 électrons (à l’exception de l’hélium dont l’orbite K est déjà complète avec 2 électrons) et ont une valence zéro ; ceux de la ^ème colonne sont monovalents et possèdent 7 électrons, c’est-à-dire qu’il leur manque un électron ; ceux de la 6^ème n’en comporte que 6, c’est-à-dire qu’il leur en manque 2 pour compléter l’orbite et ils sont bivalents ; enfin ceux de la 5^ème colonne, ont 5 électrons (il leur manque donc 3 électrons pour compléter l’orbite externe) et ils sont donc trivalents.

La relation entre la valence d’un atome et le nombre d’électrons sur l’orbite externe est donc très simple : pour les atomes des 4 premières colonnes la valence est donnée directement par le nombre des électrons périphériques, tandis que pour les atomes des 4 colonnes suivantes (on exclut toujours la 8^ème colonne où l’on trouve des triades car, pour comprendre leur cas, il faut recourir à une subdivision ultérieure de leurs orbites, ce qui est assez complexe), la valence est donnée par le nombre d’électrons périphériques qui manquent pour compléter l’orbite, c’est-à-dire pour atteindre 8 (exception faite pour l’hélium dont l’orbite est complète avec 2 électrons et qui se comporte comme les autres éléments qui possèdent 8 électrons).

Ceci étant supposé admis, on comprend que lorsque l’orbite externe n’est pas complète, il y a instabilité, car l’atome tend à perdre des électrons de cette orbite quand leur nombre est inférieur à 4, ou bien à capturer des électrons, pour la compléter quand il en possède plus de 4.

On s’explique aussi pourquoi les atomes de la dernière colonne ont une valence nulle : leur orbite externe est complète, c’est-à-dire très stable, et ainsi, ils ne tendent ni à perdre, ni à capturer des électrons. Les atomes de la première colonne et ceux de la 7^ème ont au contraire une tendance très prononcée à se combiner chimiquement pour donner lieu à des corps composés, car les premiers ont tendance à perdre un électron, tandis que les seconds tendent à en capturer un. Ainsi par exemple, le sodium et le chlore réagissent avec rapidité pour donner le chlorure de sodium (sel de cuisine) comme vous pouvez le voir de façon schématique à la figure 6.

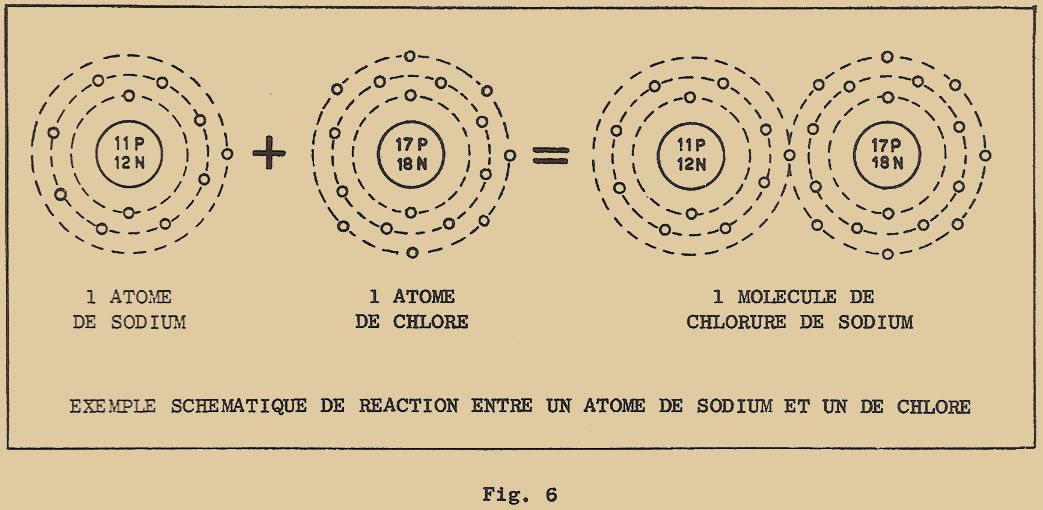
L’atome de sodium perd un électron et se trouve stable puisque l’orbite interne est complète ; l’atome de chlorure capture avidement l’électron perdu par le sodium et, complétant ainsi son orbite externe, devient ainsi à son tour très stable.

On explique de la même façon, les réactions chimiques entre les éléments bivalents de la seconde et 6^ème colonne, ou les tétravalents de la 3^ème et 5^ème colonnes. Des combinaisons chimiques peuvent avoir lieu entre des atomes qui n’ont pas la même valence et dans ce cas plus de 2 atomes interviennent dans les réactions.

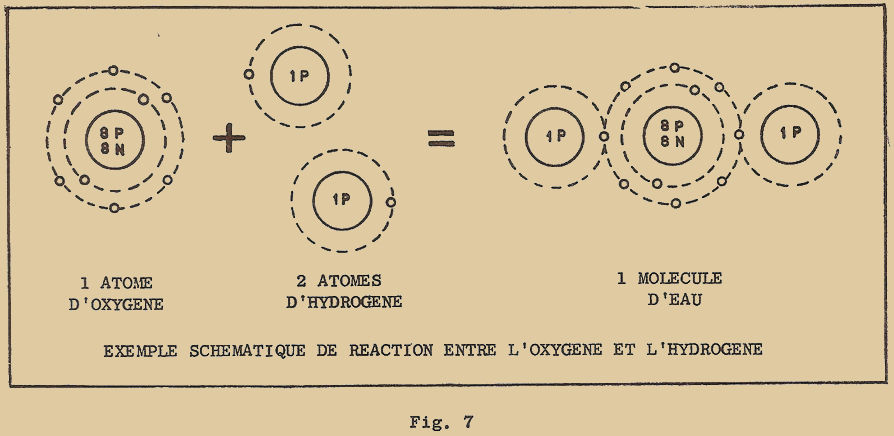
Prenons le cas par exemple de l’oxygène qui est bivalent et de l’hydrogène qui est monovalent. L’oxygène pour compléter son orbite externe a besoin de 2 électrons qui peuvent lui être fournis par 2 atomes d’hydrogène : ainsi la molécule d’eau qui en résulte est formée d’un atome d’oxygène et de 2 atomes d’hydrogène (figure 7).

Les éléments de la 5^ème colonne peuvent, ou bien perdre leurs 5 électrons périphériques, ou bien en capter 3 pour compléter leur orbite. Ils peuvent donc se comporter comme pentavalents (valence 5), ou bien comme trivalents. C’est le cas par exemple, du pentachlorure d’Arsenic, dans lequel un atome d’Arsenic a perdu ses 5 électrons en complétant les orbites d’autant d’atomes du chlore, chacun d’eux ne nécessitant qu’un seul électron.

Les électrons externes des atomes sont donc ceux qui en déterminent les propriétés chimiques, et pour cette raison portent le nom d’ÉLECTRONS DE VALENCE ; l’importance de ces électrons est donc fondamentale pour expliquer les caractéristiques des différents éléments et de leurs composés, et en particulier les semi-conducteurs utilisés dans la fabrication des transistors.

Avec la théorie électronique de la matière, le numéro d’ordre des différents éléments prit une importance beaucoup plus grande que la masse atomique considérée jusqu’alors : il fut considéré alors comme indice de la propriété de chaque élément et on l’appela NOMBRE ATOMIQUE.

Comme nous l’avons déjà vu, celui-ci indique non seulement la position exacte de l’élément dans la table de Mendeleïev, mais donne aussi directement le nombre de charges électriques positives du noyau, et par conséquent le nombre d’électrons qui tournent autour de celui-ci. Des considérations faites jusqu’à maintenant sur la masse atomique il en résulte que la DIFFÉRENCE entre le nombre (arrondi en général) représentant la masse atomique et le nombre atomique donne le NOMBRE de Neutrons qui complètent le noyau d’un atome donné.

Si nous représentons par Z le nombre atomique et par P la masse (ou le poids) atomique d’un certain élément, nous dirons que le noyau est composé de Z protons et de P – Z neutrons et qu’il y a Z électrons qui tournent autour du noyau. Ainsi pour l’oxygène, nous avons Z = 8 ; P = 16. Son noyau est donc composé de 8 protons et de 16 – 8 = 8 neutrons, et il y a 8 électrons qui tournent autour du noyau.

De ces calculs simples, on en déduit le nombre de protons et de neutrons qui sont indiqués par les lettres P et N et qui se trouvent à l’intérieur des cercles représentant les noyaux des atomes de la figure 5.

1 – 4 Isotopes

Si effectivement les atomes étaient tous formé de protons, d’électrons et de neutrons et si le neutron avait un poids égal à celui de l’atome d’hydrogène (en fait, le poids d’un neutron serait égal à celui d’un électron plus un proton puisque l’atome d’hydrogène est composé d’un électron et d’un proton), on devrait en déduire que le poids d’un atome quelconque devrait être un multiple parfait du poids de l’atome de l’hydrogène. En réalité, il suffit de jeter un coup d’œil sur la table de Mendeleïev pour voir que ce n’est pas exact : en effet, puisque la masse atomique de l’hydrogène est voisine de 1, la masse des autres éléments devrait être très voisins d’un nombre entier. C’est ce qui arrive pour certains éléments, comme He (4,0003), N (14,008), O (16,000), F (19,000), Mo (95,95) etc…mais ce n’est pas vrai pour tous. Si vous prenez par exemple le chlore (Cl) : sa masse atomique est 35,457 ce qui est bien loin de 35 ou de 36.

L’explication de ces irrégularités, fut donnée en 1912 par l’anglais SODDY, qui découvrit qu’un élément donné était formé d’un mélange de 2 "sous-produits" ayant tous des propriétés identiques, mais dont les poids pouvaient différer légèrement d’un type à l’autre : à ces "sous-produits" (ou sous éléments) on donna le nom d’ISOTOPES qui en grec, signifie "même lieu" : en effet, ayant des propriétés chimiques identiques, ils occupent la même place dans le tableau de Mendeleïev.

Un appareil extrêmement précis, mis au point quelques années après et appelé SPECTROGRAPHE DE MASSE, permit de contrôler un à un, tous les éléments connus et de déterminer que la grande majorité d’entr’eux était constitué par un mélanges d’isotopes en plus ou moins grand nombre (de deux à plus d’une dizaine).

Les isotopes d’un élément déterminé diffèrent uniquement par leur masse (poids) c’est-à-dire par le nombre de neutrons qui composent leur noyau ; ainsi si nous revenons maintenant à notre précédent exemple du chlore, nous apprenons qu’il est formé par un mélange de 2 isotopes de masse 35 et 37 et dans la proportion respective de 76% et 24% : avec une telle proportion, il en résulte un poids moyen de 35,457 comme on peut le déterminer par voie expérimentale. Les poids des isotopes sont par contre des multiples parfaits de celui de l’hydrogène, mais ne peuvent être trouvés par les déterminations normales des masses atomiques et ceci uniquement parce que la détermination est pratiquée sur un nombre considérable d’atomes et non pas sur un seul ; partant de ceci, la valeur que l’on trouve est obligatoirement une valeur moyenne des poids des différents isotopes qui constituent l’élément étudié.

1 – 5 ORDRES DE GRANDEUR

Maintenant que je vous ai expliqué la constitution de l’atome, il est bon pour fixer les idées, que je vous donne quelques ordres de grandeur sur les dimensions et les charges de ces particules microscopiques. Je vous soulignerai tout de suite que ces valeurs ne peuvent être mesurées directement (en effet, il n’est pas possible d’isoler un atome, de l’agrandir, de voir et de mesurer ses dimensions). On utilise à cette fin une méthode indirecte de calcul en partant des résultats d’expérience.

Les dimensions de l’atome (par exemple celui de l’hydrogène qui est le plus simple de tous) sont de l’ordre de grandeur du dix-millième de micron (le micron dont le symbole est µ, est égal à un millième de millimètre), c’est-à-dire qu’elles sont extrêmement petites ; en d’autres termes, nous pouvons dire qu’il faudrait mettre 10 millions d’atomes d’hydrogène à la queue leu-leu pour faire 1 mm.

Les dimensions de l’électron sont encore beaucoup plus petites : son diamètre est de l’ordre de 5 millièmes de millionième de micron : cela veut dire qu’il faudrait mettre 200.000 millions d’électrons pour faire 1 mm.

L’atome d’hydrogène a des dimensions de l’ordre de 20.000 fois plus grandes que celle d’un électron : ceci signifie que l’unique électron de l’atome d’hydrogène tourne à une grande distance (par rapport à sa dimension) du noyau. Si nous voulions réaliser une maquette d’un tel atome, il faudrait prendre une sphère de 1 mm de diamètre pour représenter l’électron et l’éloigner de 500 m du noyau.

Quant au poids (ou mieux la masse), comme je vous l’ai déjà dit, l’électron pèse environ 1840 fois MOINS que le proton, tandis que le neutron a pratiquement le même poids que ce dernier. Pour obtenir seulement un micro-gramme (c’est à dire 1 millionième de gramme) il faudrait 600.000 millions de protons (ou de neutrons). Pour obtenir un poids égal d’électrons, il en faudrait 1.840 fois plus. On peut. On peut se faire une idée du poids d’un atome, en considérant le "nombre d’Avogadro". Si nous prenons un nombre d’atomes (d’un élément donné) égal au nombre d’Avogadro, nous obtiendrons le poids en grammes de cet élément égal à sa masse atomique. Ceci signifie que 602.500 millions de millions de millions d’atomes d’oxygène par exemple auront un poids de 16 grammes (16 est en effet la masse atomique de l’oxygène) ; un même nombre d’atomes de cuivre pèsera 63,542 grammes ; le même nombre d’atomes de germanium pèsera 72,60 grammes, le même nombre d’atomes de plomb 207,21 grammes, etc…

Nous avons dit à plusieurs reprises que l’électron possédait une charge négative, dite "charge élémentaire", que le proton possédait une charge égale mais positive et que le neutron était par contre neutre ; pour avoir recours à 2 exemples.

Prenons un condensateur de 10pF et chargeons-le sous une tension continue de 100 V ; la charge accumulée sur son armature négative équivaut à 6.250 millions d’électrons.

Considérons maintenant un fil parcouru par un courant de 1µA (c’est-à-dire 1 millième de mA) ; si nous pouvions compter le nombre d’électrons qui traversent une section du conducteur, nous trouverions 6 millions de millions en une seconde.

Je vous donne ci-dessous, un tableau résumant ce que nous venons de voir :

diamètre de l’électron 5 x 10-12 mm

diamètre de l’orbite de l’hydrogène 1,06 x 10-7 mm

masse de l’électron 9,1 x 10-28 g

masse d’un proton 1,6722 x 10-24 g

masse d’un neutron 1,6747 x 10-24 g

nombre d’Avogadro 6,025 x 1023

charge de l’électron 1,6 x 10-19 coulomb

---

EXERCICES DE RÉVISION SUR LA PREMIÈRE LEÇON THÉORIQUE DE TRANSISTOR

Les réponses à ces exercices ne devront pas être envoyées à EURELEC. Je vous conseille de les consigner soigneusement dans un cahier. Vous en vérifierez l’exactitude lors de la prochaine leçon, au terme de laquelle vous trouverez les réponses exactes.

1 – Qu’appelle-t-on molécule ?

2 – Qu’appelle-t-on atome ?

3 – Par quoi exprime-t-on la valence d’un élément ?

4 – Que représente la masse atomique ?

5 – De combien de particules l’atome est-il formé et quelles en sont les propriétés ?

6 – Comment schématiquement peut-on représenter un atome ?

7 – De combien d’électrons, de protons et de neutrons est formé l’atome d’un élément, dont le numéro atomique est 17 et la masse atomique 35 ?

8 – Qu’appelle-t-on "électron de valence" et pourquoi ?

9 – Par quoi peut-on différencier les nombreux isotopes d’un élément ?

Fin de la leçon 1

---

LECON 2

1 – ÉTATS DE LA MATIÈRE

La matière se présente sous trois états différents, qui dépendent uniquement de ses conditions physiques ; nous distinguerons : l’état SOLIDE, l’état LIQUIDE, l’état GAZEUX.

Dans des conditions normales de température et de pression, la matière peut se présenter comme un SOLIDE, un LIQUIDE ou un GAZ.

1 – 1 SOLIDES, LIQUIDES, GAZ

La définition des trois états est très simple : on dit qu’un corps est solide lorsqu’il présente une forme et un volume bien définis, comme par exemple un morceau de fer, une pierre, etc… ; on appellera liquide un corps qui aura un volume bien défini, mais une forme indéterminée, comme par exemple un litre d’eau ; ainsi, le volume occupé sera toujours un litre (bien défini), mais sa forme sera celle du récipient qui le contient ; on dira enfin d’un corps qu’il est gazeux lorsque ni son volume, ni sa forme ne sont définis, de telle sorte qu’il pourra prendre la forme du récipient qui le contient, et que son volume pourra être comprimé ou dilaté à volonté.

Toutes les substances peuvent être amenées à ces trois états : il suffit de les porter à la température voulue (les chauffer ou les refroidir). Prenons par exemple l’eau qui est le composé chimique le plus répandu dans la nature. A la température normale, l’eau est liquide, mais dans les régions froides (ou si l’on vient à la réfrigérer suffisamment), elle passe à l’état solide et devient de la glace ; si nous la chauffons au contraire, elle passera à l’état gazeux (vapeur d’eau) au moment de l’ébullition.

Tout ce que nous venons de voir en ce qui concerne l’eau, reste valable pour les autres éléments ou composés chimiques. Si nous prenons du cuivre, nous pensons d’instinct à un solide parce qu’à la température ambiante il se trouve à l’état solide. Mais si nous le portons à une température supérieure à 1.080 degrés, le cuivre passera à l’état liquide, et à la température de 2.310 degrés, il passera à l’état gazeux. Si nous prenons maintenant l’oxygène nous pensons tout de suite à un gaz, mais il peut être condensé à l’état liquide si on le porte à 183 degrés en dessous de zéro et deviendra solide à une température inférieure à 218 degrés en dessous de zéro.

La température à laquelle un corps passe de l’état solide à l’état liquide, et celle où il passe de l’état liquide à l’état gazeux (ébullition) est parfaitement déterminée et dépend uniquement de la substance considérée ; ces valeurs de température sont donc caractéristiques pour chaque substance et sont appelées respectivement Température de Fusion et Température d’ébullition.

Pour savoir comment se comporte une substance déterminée lorsqu’elle passe d’un état à l’autre, on prend comme base de référence l’EAU.

Prenons de la glace à une certaine température (10° C par exemple en dessous de zéro : c’est à peu près la température de la glace d’un frigidaire) et mettons-la dans un récipient où il y a un thermomètre : celui-ci indiquera donc la température de la glace.

Chauffons lentement le récipient et notons la température à intervalles réguliers, par exemple toutes les 5 minutes : nous allons voir la température monter régulièrement jusqu’à ce que la glace commence à fondre ; à ce moment le thermomètre ne montera plus et indiquera une température constante jusqu’à ce toute la glace soit passée à l’état liquide. Ceci signifie donc que pendant ce passage de l’état solide à l’état liquide, toute l’énergie (c’est-à-dire la chaleur) fournie à la glace sert à faire fondre, c’est-à-dire à en transformer la structure interne comme nous allons le voir sous peu.

Juste à l’instant où toute la glace a fini de fondre, (ou mieux, dès que l’eau à l’état solide est passée à l’état liquide), le thermomètre recommence à monter et continue à monter jusqu’à ce que la température ait atteint la température d’ébullition.

A ce moment, de nouveau le thermomètre indiquera une température constante et toute l’énergie thermique fournie au liquide sert à en changer la structure interne : le liquide s’évapore et passe à l’état gazeux : c’est-à-dire que l’eau devient de la vapeur.

Si nous voulons représenter ce phénomène sur un graphique, nous obtenons la courbe (ligne brisée) de la figure 1 : pendant toute la période 1 – 2 le corps considéré est dans son ensemble à l’état solide et sa température va en augmentant ; pendant la période 2 – 3, il a atteint sa température de fusion et se transforme en liquide ; dans la période 3 – 4 tout le corps est à l’état liquide et sa température recommence à augmenter jusqu’à l’ébullition ; pendant la période 4 – 5 le liquide se transforme en gaz et sa température reste constante enfin, dans la période 5 – 6 le corps en entier est à l’état gazeux et la température recommence à augmenter.

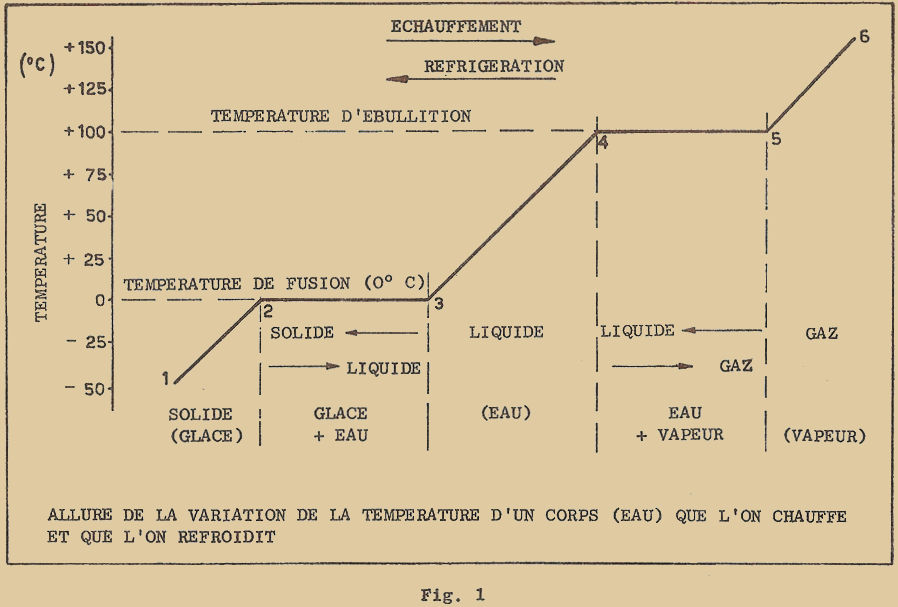
La courbe de la figure 1 peut être naturellement parcourue en sens inverse lorsque l’on part d’un gaz et qu’on le refroidit. Dans ce cas, on passera d’abord de l’état gazeux à l’état liquide, puis du liquide à l’état solide. Le passage d’un état à un autre verra encore la température rester constante et ce au moment de l’ébullition et de la fusion.

Les températures de fusion et d’ébullition sont comme nous l’avons déjà vu, des caractéristiques de chacune des substances et ne dépendent uniquement que de la pression à laquelle est soumise la substance considérée. Toutefois si la première (fusion) dépend très peu de la pression, la seconde (ébullition) en dépend beaucoup. Vous savez certainement qu’au sommet d’une montagne où l’air est raréfié (pression atmosphérique plus faible) l’eau bout à une température plus basse qu’au niveau de la mer où la pression atmosphérique est la plus élevée.

Il est bon de noter que les températures de fusion et d’ébullition de l’eau distillée au niveau de la mer, c’est-à-dire à la pression de l’atmosphère (qui équivaut à 1kg/cm2) sont prises comme références pour la détermination de l’échelle de température, appelée échelle CELSIUS. Le fait que l’eau gèle à 0° et bout à 100° n’est qu’une simple convention. On a pris l’habitude d’indiquer par un signe (+) positif, les températures supérieures à zéro degré et par un signe (-) négatif celles qui sont inférieures à celle valeur ; on écrira donc, par exemple + 25° C (° indiquant les degrés et "C" l’initiale de CELCIUS) pour indiquer une température de 25 degrés au-dessus de zéro ; on écrira de même – 7° C pour indiquer 7 degrés en dessous de zéro.

1 – 2 FORCES INTER-ATOMIQUES ET INTER-MOLÉCULAIRES – LIAISONS CHIMIQUES

Dans la précédente leçon, vous avez étudié comment les diverses substances étaient constituées par des molécules elles-mêmes formées d’un ou plusieurs atomes d’un même élément ou d’éléments composés ; les atomes, à leur tour sont formés d’un certain nombre de charges positives (protons) et d’un nombre égal de charges négatives (électrons). On peut alors presque comprendre de façon intuitive, que les forces qui lient les électrons au noyau sont de caractère électrostatique, en ce sens que les charges de signes opposés s’attirent (loi de Coulomb).

Sont encore d’origine électrostatique les forces qui lient entr’eux les atomes formant la molécule et celles qui lient ensemble les molécules des différentes substances. Ces forces ont un rayon d’action extrêmement faible, se faisant sentir à des distances très petites, de l’ordre de grandeur des atomes (de l’ordre de 1 millionième de centimètre).

En diminuant une telle distance l’intensité d’attraction augmente notablement jusqu’à atteindre une valeur maximum ; si l’on diminue encore cette distance, les forces d’attraction deviennent répulsives, ce qui signifie que deux atomes ne peuvent être rapprochés indéfiniment.

Dans le cas d’un gaz ou d’un mélange de gaz (comme c’est le cas pour l’air) dans les conditions normales, les molécules se trouvent à des distances considérables les unes des autres (par rapport à leurs dimensions évidemment) et les forces inter-moléculaires sont pratiquement nulles ; aucune liaison n’existe donc entre différentes molécules gazeuses et elles peuvent se déplacer librement. En réalité les molécules se déplacent de façon complètement désordonnée et chacune des molécules, en en rencontrant une autre, doit continuellement changer sa direction de parcours.

Les déplacements sont très petits et d’autant plus rapides que la température du gaz est plus élevée ; c’est pour cette raison que la pression d’un gaz enfermé dans un récipient augmente quand on le chauffe (par exemple, la pression des pneus de voiture augmente par échauffement quand on roule longtemps.

On peut se faire une idée sur le mouvement des molécules d’un gaz en observant une fourmilière lorsqu’ un grand nombre de fourmis se jettent sur une proie. Si l’on regarde la fourmilière à une certaine distance, on ne voit qu’une masse noire compacte, constituée par l’ensemble de toutes les fourmis. Mais si l’on se rapproche de façon à pouvoir distinguer chaque fourmi, on remarque que celles-ci se déplacent (semble-t-il) de façon désordonnée en se bousculant continuellement.

Dans le cas des liquides, les molécules sont beaucoup plus rapprochées les unes des autres et les forces inter-moléculaires ne sont plus négligeables. Dans les conditions normales, les molécules se trouvent à la distance exacte pour laquelle les forces inter-moléculaires ne sont ni attractives, ni répulsives. Mais si l’on essaie de les rapprocher un peu en comprimant le liquide, d’intenses forces répulsives apparaissent et empêchent toute compression. Les liquides sont en fait incompressibles.

Les forces d’attraction qui se manifestent quand on éloigne les molécules les unes des autres sont au contraire beaucoup moins intenses : c’est pour cette raison qu’elles ont encore un degré de liberté de mouvement appréciable, bien que plus limité que dans le cas des gaz.

Ainsi comme dans le cas précédent les molécules sont en mouvement désordonné continuel, d’autant plus rapide que la température est plus élevée, mais l’ensemble des mouvements est plus limité car les molécules sont plus rapprochées. L’augmentation de la température, en donnant une plus grande mobilité aux molécules, provoque aussi une plus grande fluidité du liquide (ce que l’on remarque en particulier dans les liquides denses) et une augmentation de son volume.

Si nous passons maintenant aux solides, nous trouvons des forces inter-moléculaires extrêmement puissantes, qui sont capables de bloquer complètement les molécules : aucun mouvement désordonné n’est plus possible, mais seulement une vibration plus ou moins intense autour du point de repos selon la température.

De cette façon, la position des molécules est rigidement fixée et le corps présente un aspect compact et indéformable.

Les forces inter-moléculaires et inter-atomiques peuvent être du type purement électrostatique comme je vous l’ai déjà signalé, quand la substance considérée est formée d’atomes électriquement polarisés. Le cas typique est celui du chlorure de sodium considéré dans la précédente leçon. Les atomes de sodium en se combinant aux atomes du chlore ont cédé à ces derniers un électron (de valence) et sont ainsi devenus électriquement positifs. Les atomes de chlore sont donc devenus négatifs ayant capté un électron : il devient évident qu’entre les deux types d’atomes nait une force d’attraction du type électrostatique. C’est ce type de liaison que l’on rencontre dans le chlorure de sodium et dans toutes les autres substances qui se comportent de même, c’est-à-dire dans lesquelles apparaissent des IONS. On appelle ION, un atome qui a perdu ou capté un ou plusieurs électrons et qui de ce fait n’est plus électriquement neutre ; les chimistes les classent en SELS, ACIDES et BASES.

D’autres types de forces de liaison, se manifestent lorsque la substance est constituée d’atomes tous identiques entr’eux, comme c’est le cas pour le germanium, le silicium, le diamant, etc… Naissent alors des forces d’attraction entre atomes, par le fait que les électrons périphériques (c’est-à-dire de valence) d’un atome ne tournent pas toujours autour de leur propre noyau, mais peuvent abandonner leur orbite propre pour passer sur celle des électrons périphériques des atomes voisins.

En d’autres termes, nous pouvons dire que les atomes s’échangent continuellement leurs propres électrons périphériques et que les forces inter-atomiques sont dues à ces échanges. On les appelle des "forces d’échange" ou énergie de cohésion et les liaisons sont dites COVALENTES. Nous verrons ultérieurement l’importance de ces liaisons dans le mécanisme du fonctionnement des semi-conducteurs.

Des forces analogues se manifestent dans le cas des métaux (cuivre, fer, etc…) où les électrons périphériques se déplacent assez librement entre les atomes sans appartenir vraiment à l’un d’eux. Les liaisons inter-atomiques dues à de tels électrons sont dites liaisons métalliques.

1 – 3 SUBSTANCES CRISTALLINES ET AMORPHES

Dans les solides, les atomes peuvent être tous d’un même type, ou bien de deux ou même plusieurs types différents ; ils peuvent non seulement être placés en des positions fixes, mais encore être alignés dans certaines directions privilégiées, et former ainsi ce que l’on appelle Réseau cristallin. La structure cristalline des solides peut être plus ou moins évidente à l’œil selon ses dimensions. Si l’on observe en effet les grains de chlorure de sodium (sels de cuisine) par exemple, obtenus en versant sur une surface lisse de l’eau fortement salée et en laissant évaporer celle-ci, on remarquera qu’ils ont tendance à former des cubes parfaits avec des facettes lisses. Dans d’autres cas (comme par exemple la fonte ou les aciers) les cristaux sont extrêmement petits et s’interpénètrent les uns dans les autres, dans ce cas la structure cristalline ne peut être mise en évidence que par examen au microscope.

Nous avons une autre catégorie de substances solides qui ne présentent aucune trace de cristallisation. De telles substances dont les molécules sont disposées de façon quelconque, sont dits AMORPHES et présentent une particularité très intéressante, typique dans le cas des verres. Si l’on prend un verre à l’état liquide et si on le laisse refroidir, on ne trouvera pas une courbe de température du type de celle de la figure 1, c’est-à-dire avec un palier horizontal (température constante). Ceci signifie que lorsqu’on diminue la température, le verre devient de plus en plus pâteux et dense pour devenir solide à la température ambiante. Mais en réalité il n’y a pas un changement net d’état. Pour cette raison, les substances amorphes sont considérées du point de vue physique comme des liquides extrêmement denses, plutôt que des solides, quoique se comportant comme tels.

1 – 4 CLASSIFICATION DES CRISTAUX

L’étude des cristaux tant du point de vue expérimental à l’aide des rayons X (radiographie) que du point de vue théorique en ce qui concerne les différentes possibilités de structure des atomes, nous amène à considérer que tous les cristaux peuvent être classés en six systèmes différents, chacun d’eux caractérisé par une configuration géométrique particulière à sa cellule élémentaire. Toutes ces configurations particulières sont des solides géométriques élémentaires aux sommets desquels sont placés les atomes et constituent la cellule. Les différents types sont représentés à la figure 2.

Nous avons les types suivants de cellule :

• Cubique : les atomes sont disposés aux sommets d’un cube, ils sont donc tous à la même distance "a" les uns des autres.
• Parallélépipède rectangle : les atomes sont disposés aux sommets d’un parallélépipède à base rectangulaire et se trouvent à des distances "a" et "b".
• Hexagonale : les atomes sont disposés aux sommets d’un prisme à base hexagonale et se trouvent encore à des distances "a" et "b".
• Orthorhombique : les atomes sont disposés aux sommets d’un prisme droit à base en losange et se trouvent à des distances "a" et "b".
Monoclinique (ou clinorhombique) : les atomes sont disposés aux sommets d’un parallélépipède non rectangle, à base rectangulaire et se trouvent à des distances "a", "b" et "c".
• Triclinique : les atomes sont disposés aux sommets d’un parallélépipède non rectangle, à base non rectangulaire et se trouvent à des distances "a, b, c".

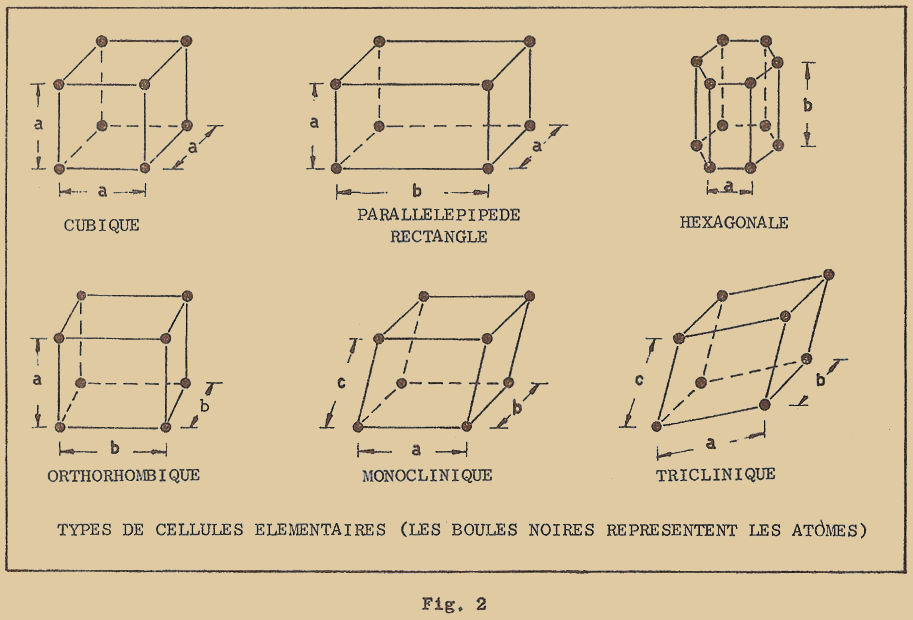
Chacun des systèmes que nous venons de voir peut être ultérieurement subdivisé en classes secondaires car, entre les sommets, les atomes peuvent se placer aussi au centre des faces ou au centre du solide.

Le système cubique en particulier, qui est celui qui nous intéresse le plus dans l’étude des semi-conducteurs, se présente sous trois espèces de structure cristalline, en plus de celle que je vous ai indiquée à la figure 2 :

Système cubique où un atome se trouve au centre du cube (figure 3)
Système cubique où un atome se trouve sur chaque face du cube (figure 4)
Système cubique tétraèdre ou diamant (figure 6)

Le système cubique où un atome se place au centre du cube est caractéristique des métaux appelés "Alcalins", tels le sodium, le potassium, le lithium. La cellule élémentaire du sodium par exemple a l’aspect indiqué à la figure 3 : les atomes du sodium se trouvent aux sommets d’un cube ainsi qu’au centre de celui-ci.

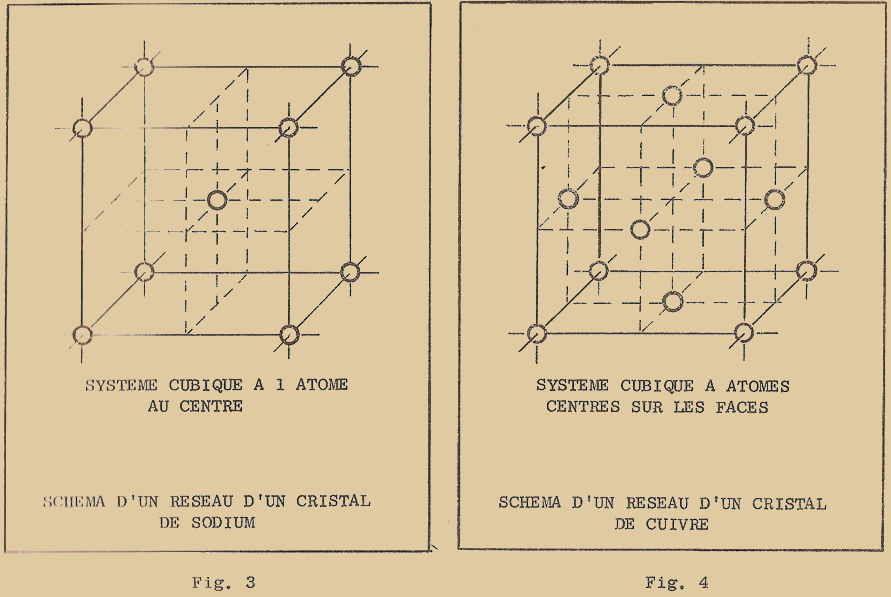
Les métaux proprement dits, tels que l’aluminium, le cuivre, l’argent, le platine, etc… cristallisent au contraire dans le système cubique, semblable à celui de la figure 4. Les atomes du cuivre par exemple se placent aux sommets d’un cube et au centre de chaque face.

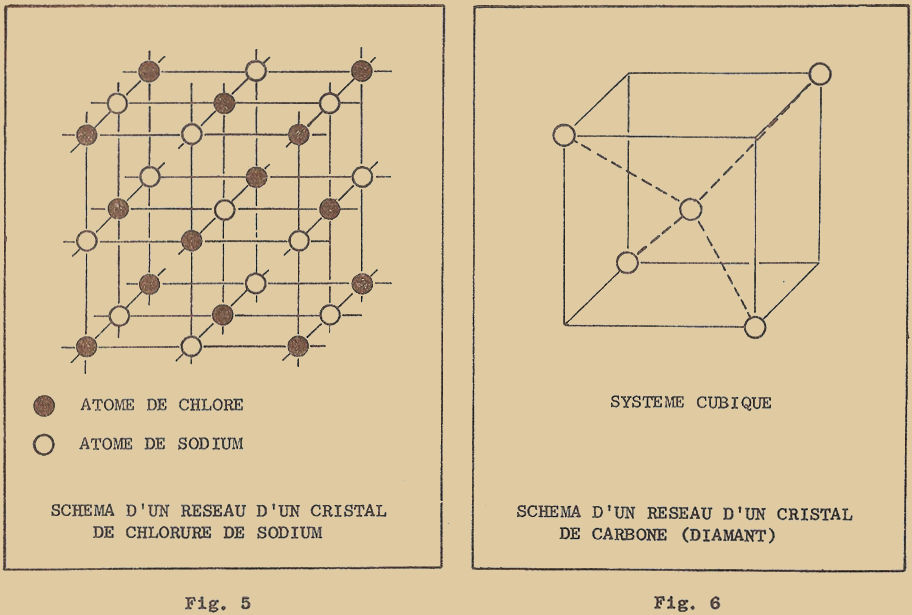
Le chlorure de sodium cristallise aussi dans le système cubique : aux sommets d’un cube se trouvent alternativement un atome de sodium et un atome de chlorure, représentés respectivement par des boules blanches et noires dans la figure 5.

Un autre type de cristal appartenant au système cubique et de très grande importance dans l’étude des semi-conducteurs est celui représenté à la figure 6. Il peut être considéré sous un certain angle comme un dérivé d’une cellule cubique avec un atome au centre, à laquelle on aurait enlevé alternativement 4 des 8 atomes disposés sur les sommets.

Le carbone qui forme le diamant, cristallise dans un tel système (d’où le nom de système cubique diamantaire). Comme vous pouvez le voir à la figure 6, l’atome central de la cellule élémentaire est lié aux 4 atomes disposés aux sommets du cube ; les liaisons sont représentées schématiquement par des lignes en pointillé.

Nous avons aussi des éléments qui peuvent cristalliser dans deux systèmes différents ; c’est le cas par exemple du carbone qui peut cristalliser dans le système cubique diamantaire et également dans le système hexagonal en formant par exemple le graphite. Les atomes de carbone sont alors disposés dans des plans parallèles aux sommets d’un hexagone.

Chaque atome de carbone se trouve encore lié aux 4 atomes, dont 3 seulement se trouvent dans le même plan, tandis que le 4^ème se trouve dans un plan adjacent (figure 7).

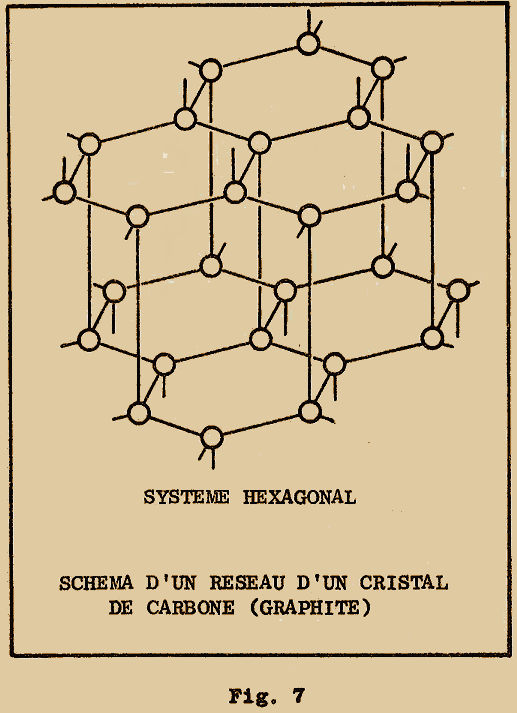
Il est important de remarquer comment un simple changement dans la disposition des atomes d’un réseau modifie complètement les caractéristiques physiques de la substance. En effet, dans les deux cas que nous venons de voir, les atomes de carbone forment le diamant ou le graphite.

Tandis que le diamant est extrêmement dur, lourd, transparent, incolore et ne conduit pas le courant électrique, le graphite est tendre, léger, opaque, noir et bon conducteur du courant.

Pour avoir une idée sur les distances entre les atomes d’un réseau cristallin, il suffit de se rappeler qu’elles sont mesurées en "microns" (dont le symbole est µ) égal à un millième de millimètre. Dans le cas du cuivre, les atomes sont placés aux sommets d’un cube élémentaire et distant de 0,4mµ seulement ; dans le cas du diamant, la distance est de 0,2 mµ et dans le cas du graphite les atomes sont disposés dans des plans distants de 0,34 mµ environ.

Quelle que soit la structure du cristal, les atomes sont liés les uns aux autres par des forces inter-atomiques intenses. Les atomes ne sont pas immobiles dans le réseau mais, comme je vous l’ai déjà dit, animés d’un mouvement vibratoire autour de leur position de repos, comme le seraient des boules vibrantes reliées les unes aux autres par des fils élastiques. L’amplitude de ces vibrations est très faible et dépend de la température du corps considéré ; plus elle est élevée, plus grandes sont les amplitudes.

Si nous chauffons un corps, les vibrations des atomes (des boules) augmentent de plus en plus et les liaisons qui les unissent (les fils élastiques) sont soumises à des forces de plus en plus grandes. Si la température dépasse une certaine limite (température de fusion) les vibrations des atomes deviennent si intenses que les liaisons se rompent : les atomes peuvent alors se déplacer librement et le corps solide est passé à l’état liquide.

Si au contraire, on refroidit le corps, le mouvement de vibration des atomes devient de moins en moins intense et la structure plus solide. Si l’on calcule la température pour laquelle les atomes deviennent immobiles, on trouve la valeur de –273°C, c’est-à-dire 273°C au-dessous de zéro.

Cette température représente une limite théorique au-dessous de laquelle on ne peut plus descendre : les atomes étant immobilisés on ne peut plus les immobiliser d’avantage.

C’est pour cette raison que la température de –273°C a été prise comme température "à zéro absolu". Pour distinguer les valeurs de température mesurées à partir du zéro absolu de celles mesurées à partir du zéro conventionnel (température de la glace fondante) on a décidé de les mesurer en degrés KELVIN (en l’honneur du physicien anglais Lord Kelvin) dont le symbole est °K.

Pour passer des valeurs conventionnelles de température, aux valeurs absolues il suffit simplement d’ajouter 273. Par exemple :

0°C = 0 + 273 = 273°K

25°C = 25 + 273 = 298°K

100°C = 100 + 273 = 373°K

Nous dirons que la glace fond à 273° absolus et que l’eau bout à 373° absolus.

Le passage inverse se fait, évidemment en soustrayant 273°. Ainsi par exemple :

300°K = 300 – 273 = 27°C

183°K = 183 – 273 = - 90°C

L’échelle des températures absolues est utilisée couramment dans l’étude de tous les phénomènes qui dépendent de la température, car les calculs viennent à être simplifiés dans quelques cas particuliers que nous verrons dans les prochaines leçons. Par contre, pour exprimer les températures normales, celles que l’on rencontre dans la vie quotidienne (température atmosphérique, etc…) il est plus commode d’utiliser l’échelle conventionnelle, c’est-à-dire parler en degrés Celsius.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 1ère LEÇON THÉORIQUE

1 – On appelle molécule la plus petite partie d’un composé chimique qui possède encore toutes les propriétés chimiques de celui-ci.

2 – L’atome est la particule d’un élément chimique qui forme la plus petite quantité susceptible de se combiner.

3 – La valence d’un élément est exprimée par le nombre d’atomes d’hydrogène qui peuvent ou pourraient se combiner avec l’élément considéré

4 – La masse atomique exprime de combien de fois l’atome considéré est plus lourd que l’atome d’hydrogène.

5 – Les atomes sont formés par des électrons, dont la charge est négative et le poids extrêmement faible, par des protons, dont la charge est positive et le poids relativement grand (par rapport à celui des électrons) et par des neutrons, électriquement neutres et dont le poids est la somme de ceux d’un proton et d’un électron.

6 – On peut représenter un atome de façon schématique par un noyau (formé de protons et de neutrons) autour duquel tournent des électrons sur des orbites plus ou moins éloignées.

7 – Le nombre d’électrons et de protons est toujours égal au nombre atomique ; l’atome considéré est donc formé de 17 électrons et de 17 protons, le nombre de neutrons est au contraire donné par la différence entre la masse atomique et le nombre atomique, et sera donc 35–17=18.

8 – Le nom d’électron de valence est donné aux seuls électrons de l’orbite externe (électrons périphériques) parce que ce sont eux seuls qui interviennent dans les réactions chimiques et que leur nombre dépend la valence.

9 – Les isotopes d’un élément diffèrent uniquement par leur masse atomique, c’est-à-dire par le nombre de neutrons contenus dans le noyau de leurs atomes.

---

EXERCICES DE RÉVISION SUR LA 2^ème LEÇON THÉORIQUE

1 – Quels sont les états de la matière et combien en connaissez-vous  ?

2 – Comment définit-on la température de fusion d’une substance  ?

3 – Comment est définie par convention l’échelle Celsius  ?

4 – Quels sont les différents types de force inter-atomiques et inter-moléculaires  ?

5 – Qu’appelle-t-on réseau cristallin  ?

6 – En combien de classes différentes, peut-on subdiviser le système cubique et comment les distingue-t-on  ?

7 – Quelles sont les différences de formation d’un diamant et d’un graphite  ?

8 – Comment se comportent les molécules d’un liquide par rapport à celles d’un solide  ?

9 – A combien de degrés Celsius correspond le zéro de l’échelle Kelvin et pourquoi l’appelle-t-on le zéro absolu  ?

Fin de la leçon 2

---

LECON 3

1 – PHÉNOMÈNE DE LA CONDUCTION ÉLECTRIQUE

Il est désormais admis que le courant électrique est constitué par un flux de charges électriques qui se déplacent sous l’action d’une force produite par un champ électrique. Dans les conducteurs solides, en particulier dans les métaux, les charges sont des électrons, c’est-à-dire négatives. Dans les liquides conducteurs les charges électriques sont constituées par des ions positifs et négatifs. Dans le premier cas, nous avons un courant électronique et le conducteur est dit de "première espèce". Dans le second cas, nous avons un courant ionique et le conducteur est dit de "seconde espèce".

1 – 1 CONDUCTEURS ET ISOLANTS

Les propriétés électriques et chimiques d’un matériau dépendent exclusivement de la configuration des atomes qui le constituent et de la manière suivant laquelle ils sont liés entr’eux ; en particulier, l’aptitude du matériau à conduire le courant électrique dépend des électrons de l’orbite périphérique, c’est-à-dire des électrons "de valence". En effet, comme je vous l’ai dit, le courant électrique est constitué d’un mouvement ordonné de charges électriques négatives (électrons) dans le conducteur ; il y a donc possibilité pour les électrons de passer d’un atome à un autre. Je vous ai dit aussi que seuls les électrons de l’orbite externe pouvaient être facilement cédés par les atomes et ce sont donc eux qui constituent le flux de courant. On peut donc dire qu’un matériau est un bon conducteur si ses atomes peuvent céder facilement des électrons, tandis qu’un bon isolant peut au contraire être défini comme un matériau à qui on ne peut arracher facilement les électrons de ses atomes.

En se rappelant ce qui a été dit dans les précédentes leçons, on peut donc prévoir que seront de bons conducteurs de courant les éléments qui ont un seul électron périphérique, car ils pourront le "lâcher" facilement.

Si nous regardons la table de Mendeleïev (voir leçon théorique 1 figure 4), nous verrons que parmi les éléments de la première colonne, nous avons le cuivre (Cu), l’argent (Ag) et l’Or (Au) qui sont les meilleurs conducteurs, c’est-à-dire des matériaux qui opposent la plus faible résistance au passage du courant électrique.

Pour étudier le phénomène de la conduction d’un matériau (pour simplifier, nous ne considérerons que les éléments simples), il faut encore considérer leur structure atomique, de façon limitée d’ailleurs car ce qui nous intéresse ce sont les électrons qui prennent une part active au phénomène de conduction. Nous n’avons donc pas besoin de représenter les atomes avec tous les électrons sur les différentes orbites mais il suffira simplement de mettre en évidence ceux de l’orbite externe.

En effet, les électrons des orbites internes sont solidement liés au noyau et chacun d’eux neutralise une charge positive du noyau (proton). Ainsi toutes les charges positives du noyau sont neutralisées sauf celles qui correspondent aux électrons de l’orbite externe. D’autre part, les neutrons peuvent être complètement négligés, car ils ne possèdent pas de charge, ni positive, ni négative.

L’atome d’un conducteur, par exemple le cuivre dont la configuration complète est indiquée à la figure 1-a, peut être encore représenté, d’une façon simplifiée mais équivalente en ce qui concerne l’étude de la conduction, par un ION ayant autant de charges positives qu’il y a d’électrons sur son orbite externe (électrons de valence) et par ces seuls électrons ; ainsi, l’atome de cuivre (Cu) ayant un seul électron périphérique, sera représenté par un ion avec la charge +1 (indiquée sur la figure 1-b, par le signe +) autour duquel tourne un électron unique.

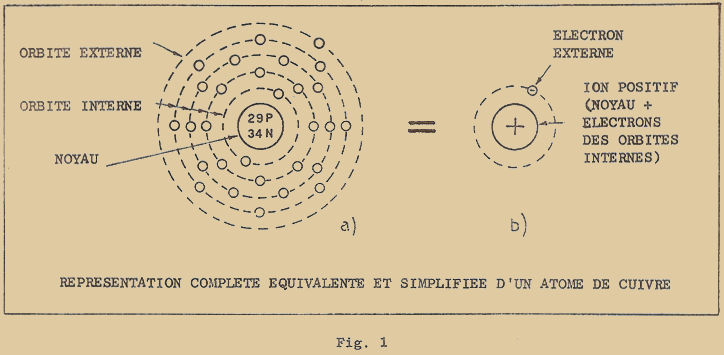
Un morceau de cuivre peut donc être représenté de façon schématique simple et conventionnelle comme un ensemble d’atomes alignés en file et sur des colonnes équidistantes de façon à indiquer sa structure interne (le cuivre cristallise en effet dans le système cubique). Il en résulte la représentation de la figure 2 : le rectangle représente le morceau de cuivre : les signes "+" cerclés symbolisent les ions positifs et le cercle indique que ces ions sont immobiles dans le réseau, le signe "-" indique que les électrons sont libres de se déplacer d’un ion à un autre, c’est pour cette raison que le signe n’est pas entouré de cercle.

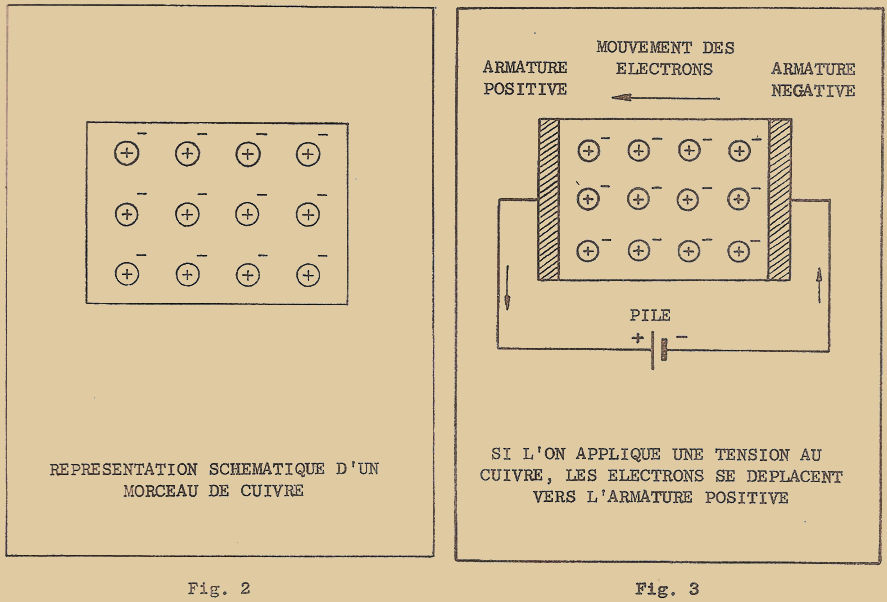
Du point de vue électrique, un morceau de cuivre est donc formé par un certain nombre de charges positives fixes, et par un nombre égal de charges négatives mobiles.

Si le cuivre n’est soumis à aucune tension les électrons tournent continuellement autour des noyaux et peuvent même de temps en temps "sauter" de l’un à l’autre. C’est de cette façon que naissent les liaisons d’échange qui, comme nous l’avons vu, constituent les forces caractéristiques qui maintiennent liés ensemble les réseaux cristallins des métaux.

Si nous appliquons maintenant une tension aux extrémités du morceau de cuivre, en le serrant par exemple entre 2 plaquettes conductrices reliées par des fils de connexion aux bornes d’une pile (figure 3) les électrons vont être repoussés par la borne négative et attirés par la borne positive. Il en découle, étant donné que les électrons peuvent se déplacer librement entre les ions immobiles, qu’ils vont se déplacer tous dans une même direction (vers la gauche d’après la figure 3). Ce flux d’électrons constitue donc le courant électrique de la pile.

Les électrons qui atteignent la plaquette positive sont dirigés par l’intermédiaire du fil de connexion vers la borne positive de la pile. De celle-ci ils se dirigent vers la borne négative de la pile puis vers l’armature négative du morceau de cuivre par l’intermédiaire du fil de liaison et puis dans le cuivre même. De cette façon, il y a autant d’électrons "aspirés" du côté gauche qu’il y en a d’émis du côté droit. À chaque instant, le nombre d’électrons présents dans le cuivre est toujours le même et égal au nombre d’ions contenus.

Les ions, possédant une charge positive subissent aussi l’influence de la tension appliquée, et précisément sont attirés par l’armature négative (à droite) et repoussés par celle de gauche (positive). Pour cette raison, ils tendraient à se déplacer de la gauche vers la droite. Mais un tel mouvement ne peut exister du fait qu’ils sont fixés dans le réseau cristallin.

Le phénomène de conduction peut aussi être considéré d’un point de vue "mécanique" en comparant le morceau de cuivre à une surface plane sur laquelle sont fixées selon un ordre déterminé, autant de boules qu’il y a d’atomes (la boule représentant le noyau de ceux-ci). D’autres billes, beaucoup plus petites (les électrons) sont disposées entre les boules et peuvent se déplacer librement, un peu comme dans un jeu de billard. Une telle représentation a été figurée sur le dessin de la figure 4.

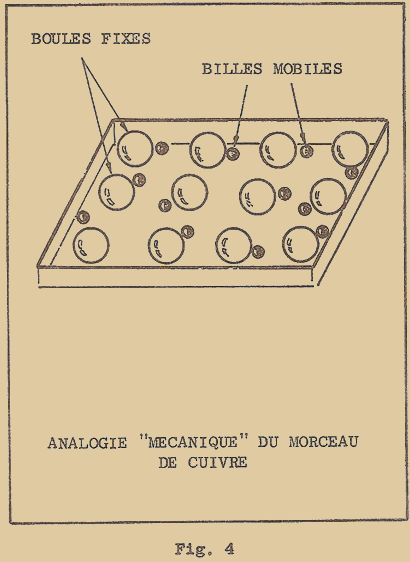
Ne pas appliquer de tension signifie alors tenir la surface plane bien horizontale, de telle façon que les billes peuvent circuler librement dans n’importe quelle direction. Appliquer une tension signifie au contraire incliner plus ou moins la surface plane (l’inclinaison sera d’autant plus grande que plus grande est la tension appliquée) et en soulevant le côté auquel on suppose appliquer la borne négative de la pile. Nous verrons alors les billes se diriger vers le côté bas, c’est-à-dire où serait branchée la borne positive, et elles prendront un mouvement continu.

Si nous voulons poursuivre plus avant la comparaison mécanique, nous pourrons comparer la pile à un tapis roulant qui recueillera les billes au point le plus bas et les ramènera au point le plus haut du plan incliné, de façon à ce qu’elles puissent recommencer leur descente (figure 5).

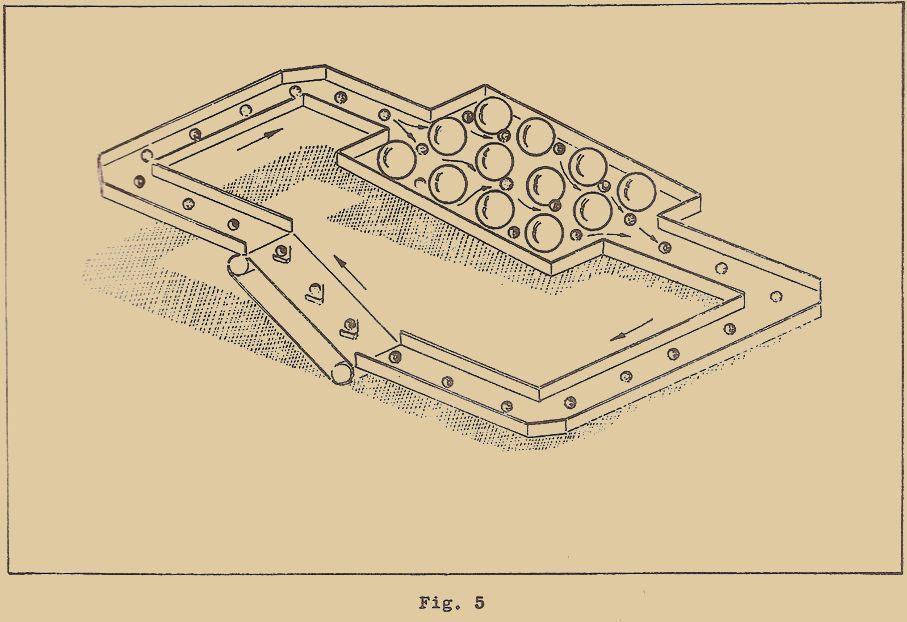
Dans leur mouvement de descente, seules quelques rares billes pourront effectuer leur trajet sans heurter de boules. Celles-ci en effet sont autant d’obstacles contre lesquels viennent se cogner les billes. À chaque rencontre, la bille s’immobilise momentanément, puis contournant la boule, reprend son mouvement de descente.

Le même phénomène a lieu dans le morceau de cuivre : dans le mouvement que leur impose la tension appliquée, les électrons sont continuellement freinés par la présence des noyaux fixes du réseau cristallin qui en limitent la mobilité.

Cette opposition des noyaux au mouvement des électrons constitue la "résistance électrique" du conducteur, c’est-à-dire dans l’exemple choisi, de notre morceau de cuivre.

Nous pouvons donc en conclure que pour être conducteur, un matériau devra être composé d’atomes qui cèdent facilement un ou plusieurs électrons : en d’autres termes, la résistance électrique, ou mieux la RÉSISTIVITÉ (ou résistance spécifique) dépend non seulement du nombre d’électrons "libres" présents, mais aussi de leur "mobilité" c’est-à-dire de la liberté de mouvement que leur permettent les ions du réseau cristallin.

A la lumière de ce que nous venons de voir, nous pouvons expliquer pourquoi en chauffant un conducteur, sa résistance augmente ; si l’on se rappelle en effet que les atomes ne sont pas immobiles, mais vibrent continuellement et rapidement autour de leur point de repos (qui est fixe) on comprend que de telles vibrations prennent une amplitude de plus en plus grande au fur et à mesure que l’on élève la température du corps. Par conséquent, l’espace occupé par un atome qui vibre est plus grand que celui qu’il occuperait s’il était complètement immobile, et il est d’autant plus vaste que les vibrations elles-mêmes sont plus importantes c’est-à-dire que la température est plus élevée.

En chauffant un conducteur, ses atomes (ou mieux ses ions) deviennent plus "encombrants" et s’opposent de plus en plus au mouvement des électrons. En d’autres termes, la RÉSISTIVITÉ du conducteur augmente avec la température.

Si l’on refroidit par contre un corps, sa résistivité diminue : les formules mathématiques montrent qu’une telle résistivité tend à devenir nulle quand la température du conducteur tend vers le zéro absolu (0°K), valeur limite que l’on ne peut atteindre en pratique.

Nous pouvons expliquer de la même façon, pourquoi augmente la température d’un conducteur parcouru par un courant. En effet, il suffit de se rappeler que les ions sont continuellement choqués par les électrons en mouvement et que leur vibration tend à devenir plus grande ; mais une augmentation de l’amplitude des vibrations équivaut à une augmentation de la température. Ainsi, plus grande est l’intensité du courant qui traverse le conducteur, plus nombreux sont les chocs subis par les ions, plus élevée est l’amplitude de leurs vibrations et plus grande enfin la température du conducteur.

Examinons maintenant un autre élément, par exemple le Carbone ; il se trouve dans la 4^ème colonne de la table de Mendeleïev, ce qui signifie que ses atomes ont quatre électrons de valence (c’est-à-dire sur l’orbite extrême).

La masse atomique du carbone est 12, son nombre atomique 6, c’est-à-dire que son atome est formé d’un noyau composé de 6 protons et de 6 neutrons, autour duquel tournent 6 électrons (figure 6-a). Comme nous l’avons fait pour l’atome de cuivre nous pouvons représenter, de façon schématique, l’atome de carbone par un cercle avec 4 charges positives (ion) et 4 électrons autour.

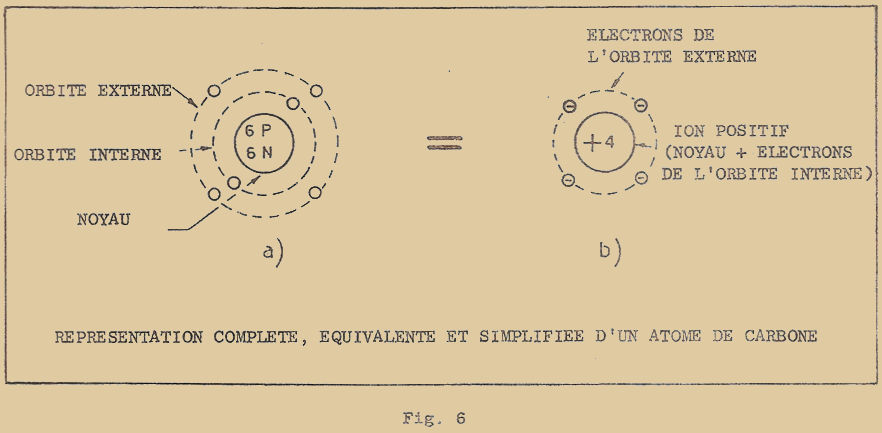
Une des 2 formes de cristallisation possible du carbone est le DIAMANT. Dans celui-ci, chaque atome a une valence 4 et s’unit aux 4 atomes voisins ; le réseau cristallin du diamant a été représenté à la figure 7 ; dans cette figure, les atomes externes ont été laissés libres pour simplifier le dessin, mais on doit bien se rappeler qu’à leur tour ces atomes se trouvent liés à d’autres atomes.

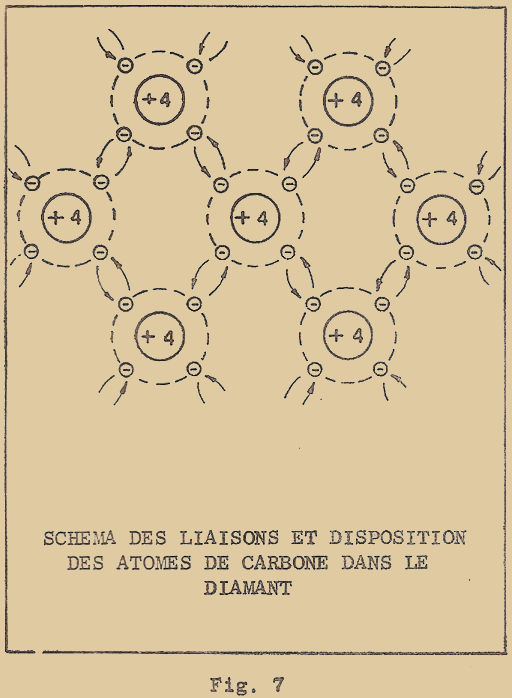
Les 4 valences de chaque atome sont ainsi réalisés par 4 électrons, un de chacun des atomes voisins ; en d’autres termes, nous pouvons dire que chaque atome complète son orbite externe en prenant 4 électrons manquants, un de chacun des 4 atomes voisins ; ainsi se crée entre les électrons d’un atome et ceux des atomes voisins, ce que l’on appelle les "liaisons de valence" (indiquées de façon schématique par les petites flèches partant de chacun des électrons) ; de telles liaisons sont extrêmement solides dans le cas du diamant, dans lequel les électrons ne peuvent se déplacer librement, mais doivent suivre leur orbite ; ainsi si l’on applique une forte tension au diamant, il ne sera pas possible d’arracher des électrons des atomes : le diamant se comporte donc comme un isolant parfait. De la même manière se comportent les isolants habituels (verre, porcelaine, matière plastique, etc…) bien que leurs molécules puissent être, dans certains cas, beaucoup plus complexes que celles du diamant. Pour tous ces corps, la raison de non-conduction du courant électrique reste la même : tous les électrons sont solidement liés aux atomes et ne peuvent se déplacer sous l’action d’une tension.

1 – 2 SEMI-CONDUCTEURS

Entre les matériaux parfaits et bons conducteurs (comme le cuivre, les métaux et leurs alliages en général) et les bons isolants (comme les composés du verre, les composés céramiques et les résines plastiques) il existe une grande catégorie de matériaux qui ne sont ni des bons conducteurs, ni des bons isolants. Parmi ces matériaux, certains présentent des propriétés électriques très particulières : les plus intéressants sont le GERMANIUM et le SILICIUM, appartenant tous deux à la 4^ème colonne de la table de Mendeleïev comme le carbone ; on a donné à ces éléments le nom de SEMI-CONDUCTEURS, car ils ne sont pas de véritables conducteurs.

L’aptitude des différents matériaux à conduire le courant électrique est exprimée de façon quantitative par leur CONDUCTIBILITÉ, dont le symbole est "σ" (qui se prononce sigma). À ce propos, il convient de rappeler que la conductibilité est définie comme l’inverse de la résistivité dont le symbole est "ρ" (se lit "ro"). Nous avons donc :

σ =1/ρ

La résistivité d’un matériau est exprimée numériquement par la résistance électrique que présente un cube de ce matériau de 1 cm de côté (figure 8) et est exprimé en Ω.cm (qui se lit "ohm multiplié par centimètre" ou plus brièvement par "ohm-centimètre).

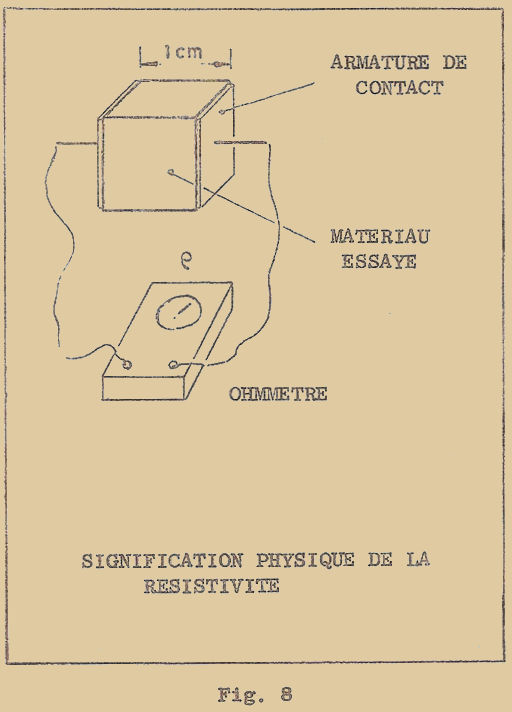
Il y a des sous-multiples et des multiples. La conductibilité qui est l’inverse de la résistivité, est donnée par un nombre qui est d’autant plus grand que la résistivité est plus petite. La conductibilité est exprimée en S/cm ("siemens divisé par centimètre" ou plus simplement en "siemens par centimètre"). Il y a des multiples et des sous-multiples. Dans certaines revues, vous trouverez la conductibilité exprimée en ("mho" par centimètre) : la conductibilité étant en effet, l’inverse de la "résistivité", les américains ont trouvé très pratique de lire le mot ohm à l’envers : d’où le nom de mho.

Je vous donne ci-dessous, les relations entre les multiples et les sous-multiples de la résistivité et de la conductibilité.

Si ρ est exprimé en :		σ sera exprimé en :
MΩ.cm		µS/cm
kΩ.cm		mS/cm
Ω.cm		S/cm
mΩ.cm		kS/cm
µΩ.cm		MS/cm

Prenons quelques exemples.

Pour le cuivre nous avons ρ = 1,7µΩ.cm

Nous aurons σ = 1/1,7 = 0,588 MS/cm = 588 000 S/cm

Pour le germanium nous avons ρ = 47Ω.cm

D’où : σ = 1/47 = 0,0213 S/cm

Pour le silicium nous avons ρ = 230kΩ.cm

D’où : σ = 1/230 = 0,00435 mS/cm = 0,000 004 35 S/cm

Pour le mica enfin (isolant le plus parfait) nous avons ρ = 100.000.000.000MΩ.cm = 10¹¹ MΩ.cm = 10¹⁷ Ω.cm

Nous aurons donc la valeur de la conductibilité

σ = 0,000.000.000.01 µS/cm = 0,000.000.000.000.000.01 S/cm = 10^-17 S/cm

C’est-à-dire que pratiquement la conductibilité est nulle

En comparant les différentes valeurs de conductibilité, on peut dire que le cuivre est environ 27,5 millions de fois plus conducteur que le germanium et environ 135.000 millions de fois plus conducteur que le silicium.

Fermons maintenant cette parenthèse sur la résistivité et la conductibilité, et revenons-en aux semi-conducteurs, en particulier au germanium (Ge) et au silicium (Si). Leurs caractéristiques atomiques sont les suivantes : (voir tableau ci-après)

	Ge	si
Nombre atomique	32	14
Masse atomique	72,60	28,6
Protons	32	14
Neutrons	40	14
Electrons	32	14
Electrons périphérique	4	MS/cm
Masse spécifique	5,32 g/cm3	2,33 g/cm3
Température de fusion	958°C	1420°C
Résistivité à 25°C	47 Ω.cm	230 000 Ω.cm

Étant tétravalents comme le carbone, les atomes de germanium et du silicium peuvent être représentés de la même manière que celle indiquée à la figure 6-b, c’est-à-dire par un ion de charge positive + 4, et par 4 électrons ; la structure du réseau cristallin est la même que celle du carbone représentée à la figure 7. La représentation complète des atomes de germanium et de silicium est indiquée à la figure 9

Si la structure du germanium et du silicium est la même que celle du carbone, on peut penser que ces éléments semi-conducteurs doivent être des isolants parfaits : en effet chaque atome est lié aux 4 atomes voisins par ses 4 électrons de valence qui eux-mêmes sont liés fortement à leur orbite et ne peuvent donc participer au phénomène de conduction. La différence qui existe entre le carbone et le germanium (ou le silicium), et qui fait que ce dernier est un semi-conducteur et non un isolant, réside précisément dans les liaisons qui unissent les différents atomes ; tandis que dans le carbone, ces liaisons sont extrêmement solides comme nous l’avons vu et ne peuvent se rompre en aucun cas, dans le germanium (et le silicium) elles sont beaucoup plus fragiles et peuvent se rompre assez facilement. La rupture d’une liaison signifie en première approximation (nous verrons plus tard ce qui arrive exactement au moment d’une telle rupture) qu’un électron se détache de son orbite et se déplace librement dans réseau cristallin avant d’être capté par un autre atome auquel manque précisément un électron perdu précédemment.

Dans un cristal de germanium, il y a en permanence un certain nombre d’électrons vagabonds : c’est à quoi est due la conductibilité.

La rupture des liaisons est due aux vibrations des atomes, vibrations qui comme nous l’avons vu, sont dues à la température à laquelle est soumis le cristal. Plus la température est élevée, plus grandes sont les amplitudes des vibrations des atomes, et plus il y a de ruptures des liaisons, d’où un nombre plus grand d’électrons qui quittent leur orbite. Il en résulte que plus on augmente la température d’un semi-conducteur et plus on augmente sa conductibilité, c’est-à-dire que l’on diminue sa résistivité, exactement l’inverse de ce qui se produit pour les conducteurs métalliques.

Il faut remarquer cependant, qu’avec l’augmentation de la température, il y a une opposition plus grande de la part des atomes au parcours des électrons, car les chocs augmentent de la même manière que pour le cuivre, et il y a en fait une "diminution" de la mobilité des électrons. Mais en même temps, on constate une augmentation beaucoup plus grande du nombre d’électrons "libérés", ce qui fait qu’en définitive le second phénomène l’emporte, et il y a augmentation de la conductibilité : ceci est la propriété fondamentale qui distingue les semi-conducteurs des conducteurs proprement dits.

Si le germanium (ou le silicium) était porté à la température du zéro absolu (0°K, c’est-à-dire – 273°C), les atomes seraient parfaitement immobiles dans le réseau cristallin, aucune liaison ne pourrait être rompue et il n’y aurait aucun électron libre : le semi-conducteur se comporterait alors comme un isolant parfait de la même manière que le diamant.

À titre d’exemple, je vous ai représenté à la figure 10, la variation de la valeur de la résistivité du germanium pour une température comprise entre 273 et 373°K (correspondant à l’intervalle de 0°C à 100°C) ; comme vous pouvez le voir, la diminution de la résistivité est extrêmement rapide : de 190 Ω.cm à 0°C, elle descend à 47 Ω.cm environ à 25°C et tombe à 3 Ω.cm à 100°C.

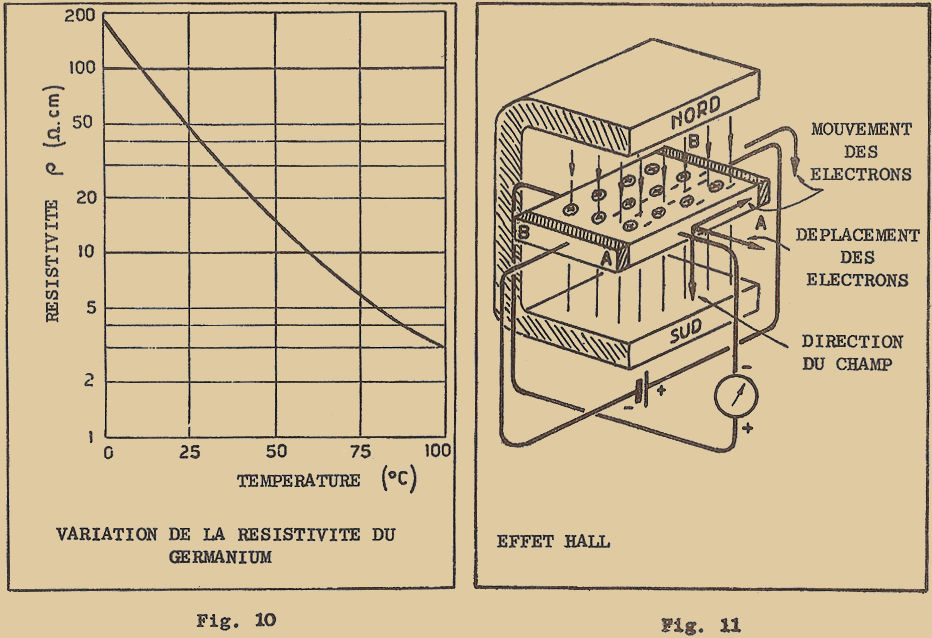
2 – EFFET HALL

L’effet Hall (du nom du savant anglais qui le découvrit en 1879) peut être illustré par une expérience très simple.

Prenons un conducteur quelconque et plaçons-le dans un champ magnétique uniforme, de façon à ce que les lignes de flux de ce dernier soient perpendiculaires au conducteur ; de telles conditions d’expérience peuvent être facilement obtenues, en plaçant le conducteur entre les pièces polaires d’un aimant permanent, comme l’indique la figure 11.

Si maintenant nous faisons parcourir le conducteur par un courant électrique, les électrons vont être soumis à l’action du champ magnétique et tendront à se déplacer dans une direction perpendiculaire à leur direction de mouvement ; dans un sens déterminé par les lignes de flux du champ magnétique. Par exemple, si le champ est dirigé vers le bas, les électrons tendront à se déplacer vers la droite par rapport à la direction de leur mouvement.

L’action du champ magnétique fait que le courant électrique n’est plus distribué uniformément dans le conducteur, mais qu’il est plus dense d’un côté que de l’autre, comme vous pouvez le voir clairement sur la figure 11. Les électrons de circulation vont donc parcourir le conducteur du côté AA.

Ceci entraîne une conséquence que l’on peut vérifier expérimentalement : si nous regardons le conducteur, nous voyons que sur le côté AA, il y a des charges négatives (électrons) et que par contre sur le côté BB restent des charges positives, constituées par les ions fixes du conducteur dont les charges ne sont plus neutralisées par les électrons qui ont quitté cette zone. Entre les 2 côtés du conducteur, apparait donc une différence de potentiel électrique, due à la séparation des charges de signe contraire.

Si nous branchons un voltmètre sensible sur les côtés du conducteur nous pourrons mesurer une tension dont les polarités sont indiquées sur la figure 11 : négative du côté AA, positive du côté BB. L’effet Hall consiste donc dans l’apparition d’une telle tension, dont la valeur permet de calculer la "mobilité" des charges qui constituent le courant dans le conducteur.

Les autres phénomènes, caractéristiques des semi-conducteurs, seront expliqués par la suite, en se référant à l’effet Hall.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 2^ème LEÇON THÉORIQUE

1 – Les états possibles de la matière sont au nombre de 3 : l’état solide, l’état liquide et l’état gazeux.

2 – La température de fusion d’une substance est celle pour laquelle la substance considérée passe de l’état solide à l’état liquide.

3 – L’échelle de température Celsius a été définie en prenant respectivement 0°C. et 100°C, comme les deux températures de fusion et d’ébullition de l’eau distillée à la pression de l’atmosphère (au niveau de la mer).

4 – Les forces inter-atomiques et inter-moléculaires peuvent être du type électrostatique, comme dans le cas du chlorure de sodium, ou des forces d’échange comme dans le cas des métaux et des substances formées par un seul type d’atome.

5 – Un réseau cristallin est la disposition régulière des atomes au sein d’un cristal.

6 – Le système cubique est divisé en 3 classes qui sont respectivement :

système où un atome se trouve au centre du cube
système où un atome se trouve sur chaque face du cercle
système tétraèdre.

7 – Le diamant et le graphite diffèrent uniquement par le mode de cristallisation des atomes du carbone : le premier cristallise dans le système cubique, le second dans le système hexagonal.

8 – Les molécules d’un liquide sont en mouvement désordonné continuel ; les molécules d’un solide au contraire se trouvent en des points bien déterminés, autour desquels elles accomplissent un mouvement de vibration.

9 – Le zéro de l’échelle Kelvin correspond à - 273 degrés Celsius. Il est appelé zéro absolu parce qu’il représente la température minimum que l’on peut théoriquement atteindre et à laquelle il y a arrêt complet du mouvement des molécules.

---

EXERCICES DE RÉVISION SUR LA 3^ème LEÇON THÉORIQUE

1 – De quoi dépend l’aptitude d’un matériau à bien conduire le courant  ?

2 – Comment peut-on représenter un atome de façon simplifiée mais équivalente du point de vue électrique  ?

3 – De quoi dépend la résistivité d’un conducteur  ?

4 – Comment varie la résistivité d’un conducteur quand on chauffe celui-ci et pourquoi  ?

5 – Qu’appelle-t-on conductibilité d’un matériau et en quelles unités l’exprime-t-on  ?

6 – Pourquoi le diamant est-il un isolant parfait, tandis que le germanium ayant une structure cristalline semblable ne l’est pas  ?

7 – Pourquoi dans un semi-conducteur la résistivité diminue-t-elle, au lieu d’augmenter, lorsque croît la température comme cela se produit dans les conducteurs  ?

8 – Quelle serait respectivement la résistivité d’un conducteur et celle d’un semi-conducteur, si on les portait à 0°K  ?

9 – En quoi consiste l’effet Hall  ?

Fin de la leçon 3

---

LECON 4

1 – SEMI-CONDUCTEURS DOPÉS

Pour augmenter la conductibilité d’un semi-conducteur, il suffit d’introduire dans le réseau cristallin, une très faible quantité d’impuretés de façon à créer à l’intérieur du réseau, des "irrégularités" qui permettent alors d’obtenir des charges "libres" que l’on appelle les Porteurs d’Électricité.

On peut utiliser comme "impureté", tout au moins théoriquement, n’importe quel élément dont la valence est différente de celle du semi-conducteur, c’est-à-dire différente de 4. On utilise normalement les éléments de valence 5 ou 3, c’est-à-dire ceux qui de trouvent dans la 5^ème ou la 3^ème colonne de la table de Mendeleïev ; pour ce rôle, les éléments pentavalents suivants peuvent être utilisés : Phosphore (P), Arsenic (As) et Antimoine Sb) ; les éléments trivalents utilisés peuvent être :

BORE (B), ALUMINIUM (AL), GALLIUM (GA), INDIUM (In).

Les premiers possèdent 5 électrons périphériques et peuvent donc être représentés de façon schématique, par un ion de charge positive + 5 et par 5 électrons tournant autour. Les seconds ont au contraire 3 électrons sur l’orbite périphérique et on peut les représenter par un ion de charge positive +3 entouré de 3 électrons.

Les quantités d’impuretés que l’on introduit dans le semi-conducteur (germanium ou silicium) sont infimes : il suffit de penser qu’en introduisant seulement 1 µg (c’est-à-dire un millionième de gramme) de bore dans 100 g de germanium, la résistivité de ce dernier passe de 47 Ω.cm à moins de 1 Ω.cm.

L’ordre de grandeur de la proportion d’impuretés que l’on utilise dans ce cas est alors de l’atome d’impuretés pour 30 millions d’atomes de germanium. L’opération qui consiste à introduire des impuretés dans le semi-conducteur s’appelle quelquefois DOPAGE et le semi-conducteur ainsi traité est dit DOPÉ ; le dopage peut être faible, moyen ou fort, selon la quantité d’impuretés que l’on y a introduite.

Entre les différents éléments susceptibles d’être utilisés, les plus courants sont l’arsenic (pentavalent) et l’indium (trivalent). Si nous prenons ces 2 éléments, leur représentation schématique peut être celle de la figure 1 et sera valable pour tout autre type d’impuretés. Nous étudierons par la suite, surtout le cas du germanium, mais les mêmes considérations sont valables pour le silicium.

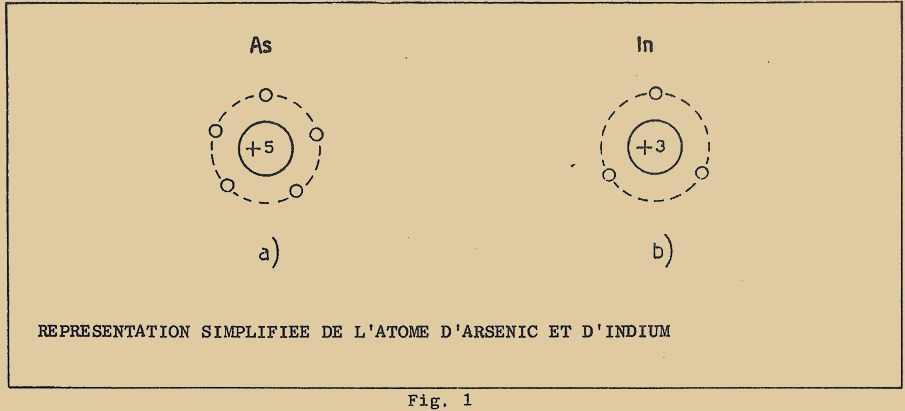
Bien que le fait de "doper" le semi-conducteur en y introduisant des impuretés, soit pentavalentes soit trivalentes provoque, dans les deux cas, une diminution de la résistivité du semi-conducteur ; le comportement de celui-ci du point de vue électrique, est totalement différent dans chacun des cas.

C’est grâce à cette différence de comportement qu’est rendu possible le fonctionnement des diodes et des transistors ; nous étudierons séparément ces deux cas, ainsi que le comportement des atomes d’impuretés introduits dans le semi-conducteur et nous verrons comment se produit le phénomène de conduction.

1 – 1 DOPAGE PAR LES ÉLÉMENTS PENTAVALENTS - SEMI-CONDUCTEUR DU TYPE N

Si on introduit des atomes d’arsenic dans le réseau cristallin du germanium, il est évident qu’ils vont provoquer des irrégularités dans le réseau même pour la simple raison qu’ils ont une constitution différente (en particulier, ils possèdent 5 électrons de valence, tandis que les atomes de germanium en ont seulement 4).

Considérons maintenant un atome d’arsenic entouré d’atomes de germanium.

Nous remarquons tout de suite, que pour effectuer ses liaisons avec 4 atomes de germanium qui l’entourent, il utilisera seulement 4 électrons ; le 5^ème ne trouvant pas d’atome avec lequel il formerait une liaison, reste en surnombre. On peut penser dès lors qu’un tel électron pourra quitter facilement son orbite et voyager dans le réseau cristallin.

En réalité, on constate que même à la température ambiante, l’agitation thermique des atomes (due à leurs vibrations continuelles) est déjà suffisante pour éjecter de tels électrons de leur orbite et les "libérer", chaque atome d’arsenic donnant un électron "libre" ; c’est-à-dire que dans le germanium dopé, il y aura autant d’électrons libres qu’il y a d’atomes d’arsenic introduits. C’est à ces électrons que nous devrons la possibilité de passage du courant électrique dans le germanium et c’est pour cette raison qu’on les appelle des PORTEURS (sous-entendu d’électricité).

Les atomes d’arsenic (ainsi que les autres éléments pentavalents) sont dits des DONNEURS, car ils "donnent" un électron.

En regardant la figure 2, nous pouvons voir que l’atome d’arsenic est formé d’un ion ayant 5 charges positives et de 5 électrons (charges négatives), ce qui le rend électriquement neutre. Mais après qu’il ait cédé un de ses électrons 4 seulement des 5 charges positives sont compensés par les 4 électrons restants, ce qui signifie du point de vue électrique, que l’atome d’arsenic se comporte comme une charge positive et qu’il peut être représenté plus simplement, par un ion ayant une> seule charge positive et par un électron (celui qui a été cédé).

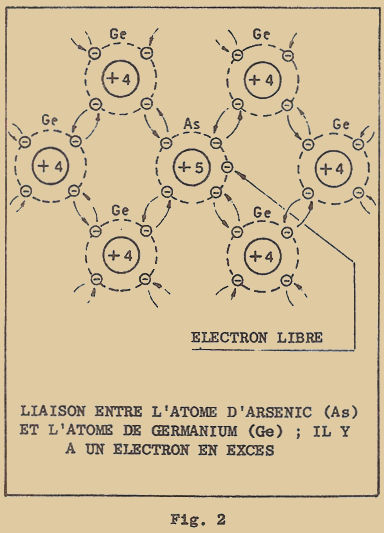
Il faut encore remarquer que tous les atomes de germanium ont leurs électrons solidement liés et qu’ils ne participent pas à la conduction, exception faite pour quelques rares atomes dont une liaison se rompt, mais ils sont si peu nombreux par rapport aux atomes d’arsenic que l’on a introduits, qu’ils peuvent être négligés.

La représentation schématique d’un bloc de germanium dopé par de l’arsenic (ou d’une façon plus générale, d’un semi-conducteur dopé par un élément pentavalent) peut donc être faite en dessinant seulement les atomes DONNEURS par autant de cercles avec le signe + (ions positifs fixes dans le réseau) et par autant de signes – (électrons libres, qu’on appelle les PORTEURS). Voir la figure 3.

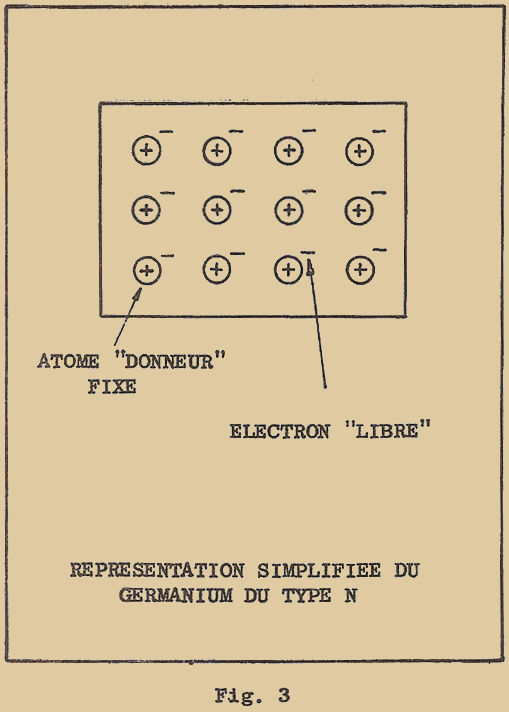
En se rappelant la représentation d’un bloc de cuivre (voir leçon précédente) on peut remarquer qu’elle ne diffère pas de celle d’un bloc de germanium dopé par un élément donneur ; pour expliquer le phénomène de la conduction, il suffira de refaire le raisonnement vu à propos du cuivre. Comme la conduction du courant est due à des électrons, c’est-à-dire à des charges négatives, puisque l’on a introduit dans le germanium des impuretés du type DONNEUR, le germanium est dit du type N (N pour "négatif").

Bien que le phénomène de la conduction soit le même, le germanium N présente une conductibilité beaucoup plus faible que celle du cuivre. Pour l’expliquer, il suffit de se rappeler que dans le cuivre, pour chaque atome du réseau cristallin il y a un électron libre, tandis que dans le cas du germanium, il y en a très peu : quelques électrons libres pour des millions d’atomes du réseau (il n’y a en effet qu’un seul électron libre seulement pour un atome donneur).

Il en résulte donc que dans le germanium nous avons une CONCENTRATION d’électrons (la concentration d’électrons est indiquée par la lettre n et donne le nombre de porteurs négatifs, c’est-à-dire d’électrons libres dans 1 cm³ du matériau considéré), beaucoup plus faible que dans le cuivre. D’autre part, la MOBILITE des électrons (la mobilité est indiquée par la lettre µ_n et exprime la vitesse en cm/s des électrons qui se trouvent dans un cube du matériau considéré de 1 cm de côté, quand on lui applique une tension de 1 V) dépend de la structure du réseau cristallin ; elle est beaucoup plus faible dans le germanium que dans le cuivre. En conclusion, la conductibilité est d’autant plus élevée que plus grandes sont la concentration n et la mobilité µ_n : ainsi, on comprend pourquoi la conductibilité du germanium est beaucoup plus faible que celle du cuivre, et aussi qu’elle augmente avec le dopage.

1 – 2 DOPAGE AVEC DES ÉLÉMENTS TRIVALENTS – SEMI-CONDUCTEURS DU TYPE P

Si dans le réseau cristallin du germanium, on introduit des atomes d’indium (impureté trivalente) on obtient une fois encore, une irrégularité dans le réseau même. Comme on peut le voir sur la figure 4, l’atome d’indium n’ayant que 3 électrons de valence, ne pourra les lier qu’avec 3 des 4 atomes de germanium voisins. L’irrégularité est cette fois représentée par un "manque" d’électrons sur l’orbite de l’atome d’indium et de la liaison correspondante avec l’atome de germanium. Pour mieux mettre en évidence un tel fait, l’électron manquant a été représenté par un cercle en pointillé (sans le signe -) auquel on donne le nom de LACUNE (ou TROU), et la liaison manquante est indiquée par une flèche en pointillé.

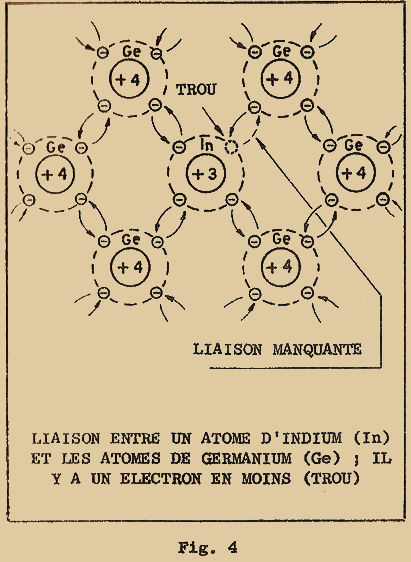
L’atome d’indium, pour compléter son orbite, va chercher à capturer un électron d’un atome voisin ; si dans le voisinage une liaison vient à se rompre entre 2 atomes de germanium (nous avons vu dans la dernière leçon, que sous l’effet de l’agitation thermique, des liaisons se rompaient et se reformaient en permanence), il y aura libération d’un électron qui sera immédiatement capturé par l’atome d’indium.

Il en résultera alors que le "trou" ("lacune") sur l’orbite de l’indium sera "comblé" et disparaîtra, mais il se créera en même temps un nouveau trou sur l’orbite de l’atome de germanium qui vient de perdre son électron comme nous pouvons le constater sur la figure 5.

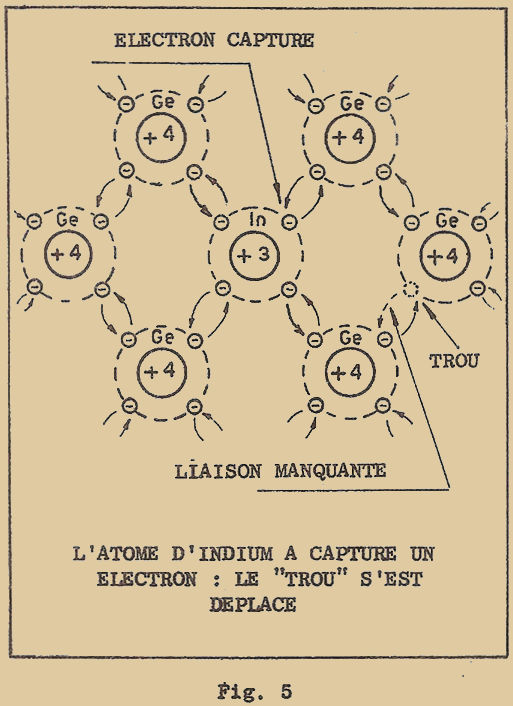
Maintenant ce sera au tour de ce dernier atome de germanium à chercher à capturer un électron libre pour "combler" son trou, et il va y avoir déplacement du "trou" (lacune).

Je tiens à vous signaler que j’emploierai par la suite indifféremment les termes de "trou" et de "lacune" afin de vous habituer à ces 2 mots qui sont couramment utilisés dans la techniques des semi-conducteurs.

En considérant que les électrons manquants sont des lacunes, on peut voir qu’il existe une certaine analogie avec le cas précédent, où le dopage était fait avec de l’arsenic : dans le cas précédent, l’atome d’arsenic "cédait" un électron libre ; ici l’atome d’indium "capture" un électron en "cédant" un trou. L’atome d’indium (ou d’un élément trivalent quelconque) est appelé pour cette raison ACCEPTEUR, puisqu’il "accepte" un électron.

Mais allons plus avant. En regardant la figure 5, nous pouvons noter que l’atome d’indium ayant "accepté" un électron, possède maintenant 4 électrons et seulement 3 charges positives : il se comporte donc comme un ion ayant une charge négative. D’autre part, l’atome de germanium qui a cédé un électron, se comporte comme un ion ayant une charge positive, puisque seulement 3 d’entr’elles sont compensées par les 3 électrons restant. Si nous considérons le "trou" au lieu de l’électron, nous pourrons dire que l’atome d’indium a cédé un trou et que l’atome de germanium a reçu un trou ; mais dans cet échange, l’atome de germanium est devenu un ion ayant une charge positive et on peut ainsi penser qu’une telle charge positive lui a été donnée par le trou qu’il a capté.

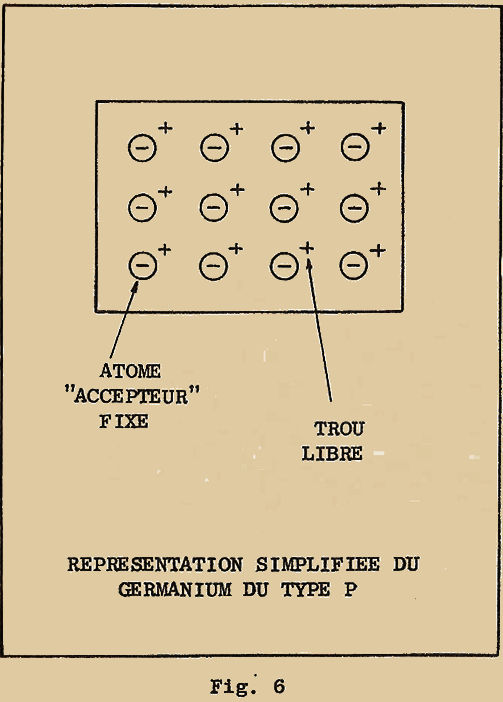
En conclusion, le trou peut être considéré comme une charge positive libre, puisqu’il se comporte comme tel.

Ainsi le germanium dopé par un élément trivalent pourra maintenant être représenté de façon simplifiée, mais équivalente du point de vue de son comportement électrique, en ne dessinant que des atomes "accepteurs", équivalents à des ions négatifs (cercles avec signe -) immobiles dans le réseau et avec une charge positive libre (indiquée par le signe +) comme on peut le voir sur la figure 6.

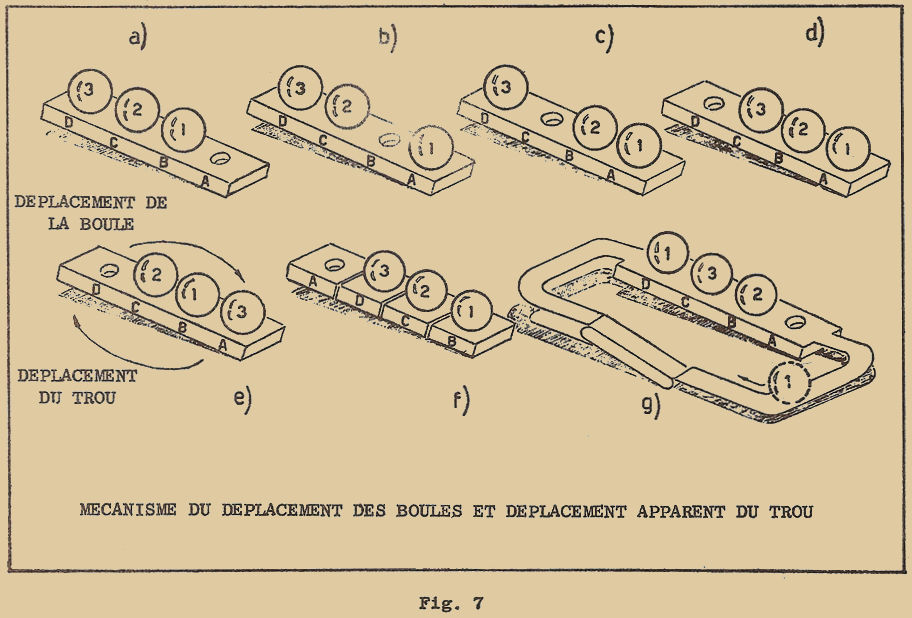
La conduction du courant se fait à l’aide des charges libres qui maintenant sont positives ; c’est pour cette raison qu’un semi-conducteur dopé par un élément accepteur (trivalent) est dit du type P ("P" comme positif).

Pour mieux comprendre comment se comportent les lacunes en tant que charges positives et comment par leur intermédiaire il peut y avoir conduction, on peut recourir à une analogie mécanique.

Imaginons un support ayant 4 trous dont 3 sont occupés par des boules. Inclinons ce support comme sur la figure 7-a les boules restent immobiles, "encastrées" dans leurs trous respectifs. Si maintenant on fait sortir la boule 1 du trou B, elle va, grâce à la pente, venir tomber dans le trou A (figure 7-b), laissant libre le trou B. Si maintenant on fait sortir la boule 2 du trou C, elle ira dans le trou B (figure 7-c) ; enfin la boule 3 ira de même dans le trou C, en libérant le trou D (fig. 7-d).

On peut remarquer que la même disposition que celle de la figure 7-d (naturellement on ne tient pas compte du numérotage des boules qui sont toutes identiques) serait apparue si l’on avait directement déplacé la boule 3 du trou D dans le trou A (figure 7-e) : ceci signifie que le déplacement d’un cran de toutes les boules revient à déplacer une seule boule de 3 crans. La disposition de la figure 7-d peut encore s’obtenir en découpant le support et en enlevant le morceau correspondant au trou A pour le replacer à l’autre extrémité du support (figure 7-f) ; ceci signifie donc que déplacer une boule de 3 crans de gauche à droite équivaut à déplacer le trou de 3 crans de droite vers la gauche.

Lorsque l’on a obtenu la disposition de la figure 7-d, on peut faire sortir la boule 1 du trou A et la ramener de nouveau au trou D, par l’intermédiaire du "tapis roulant" (figure 7-g) ; de cette façon, on revient à la disposition de la figure 7-a, et tout peut recommencer.

En définitive, on en vient à considérer le phénomène ci-dessus sous l’aspect suivant : dans le circuit extérieur, c’est-à-dire celui qui relie l’extrémité droite du support à l’extrémité gauche, ce sont les boules qui de déplacent. Au contraire, en ce qui concerne le circuit support (intérieur pourrait-on dire) au lieu de considérer que ce sont les boules qui se déplacent d’un cran à chaque fois, on peut dire plus simplement que ce sont les trous qui se déplacent de la droite vers la gauche.

Revenons maintenant au phénomène électrique ; plaçons un morceau de germanium du type P (comme celui de la figure 6) entre 2 armatures reliées aux bornes d’une pile (figure 8) : la pile va "envoyer" dans le bloc de germanium par l’intermédiaire des fils de liaison, des électrons, qui vont diffuser à l’intérieur du germanium et "neutraliser" les trous qui se trouvent dans la partie gauche du germanium. Les trous qui se trouvent dans la partie de droite seront alors "attirés" par l’armature de gauche qui est négative et repoussés par l’armature de droite qui est positive, puisqu’ils se comportent comme nous l’avons vu, comme des charges positives. Quand ils auront atteint l’extrémité gauche, ils vont disparaître, car ils vont se combiner avec d’autres électrons, injectés par l’armature négative.

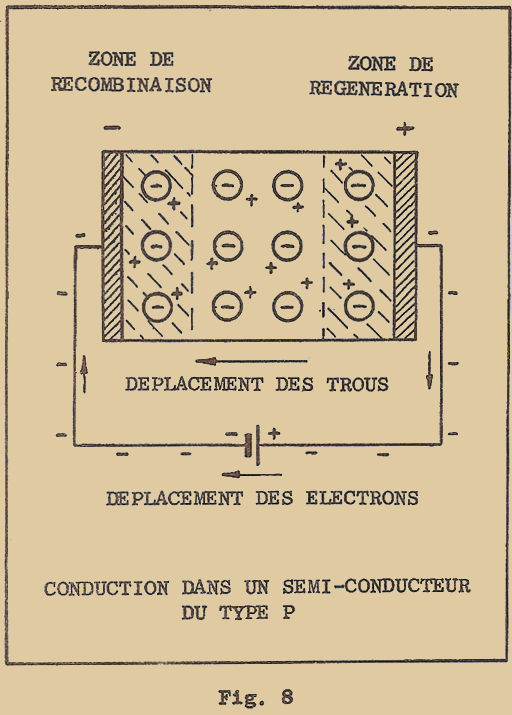
Étant donné d’une part que des électrons sont injectés par l’armature négative et qu’ils ne peuvent atteindre l’armature positive, et que d’autre part, le courant qui parcourt les fils de liaison de droite et de gauche est le même, (en ce sens qu’il est formé par un même nombre d’électrons mis en mouvement par la pile), on peut en déduire que la pile est capable d’"extraire" autant d’électrons du bloc de germanium dans le voisinage immédiat de l’armature positive, qu’elle peut "émettre" dans celui-ci du côté de l’armature négative.

Si nous nous rappelons la constitution interne du bloc de germanium P (figure 4), nous voyons que pour extraire des électrons du semi-conducteur, nous ne pouvons que leur faire "quitter" leur orbite. Mais extraire un électron de son orbite signifie que l’on crée un trou (trou laissé par l’électron) et ainsi le phénomène de la conduction dans un semi-conducteur P peut s’expliquer de la façon suivante :

Dans le voisinage immédiat de l’armature de gauche, nous avons une zone de RECOMBINAISON, dans laquelle les électrons injectés par l’armature de gauche "tuent" les trous : les électrons et les trous se recombinent et leurs charges (de signe opposé) se neutralisent réciproquement. Dans le voisinage immédiat de l’armature de droite, nous avons au contraire une zone de RÉGÉNÉRATION à partir de laquelle on extrait des électrons du semi-conducteur et dans laquelle se forment les nouveaux trous : ceux-ci, attirés par l’armature négative et repoussés par l’armature positive, se déplacent vers la gauche, atteignent la zone de recombinaison et se recombinent avec d’autres électrons.

Les électrons qui sont extraits du côté droit sont réinjectés du côté gauche et referment ainsi le cycle.

Alors que dans les fils de liaison, le courant est constitué par un flux d’électrons qui circulent dans un certain sens, à l’intérieur du semi-conducteur P il est constitué par un flux de lacunes (trous) qui circulent en sens inverse, c’est-à-dire que la conduction a lieu par le déplacement de charges positives au lieu de négatives.

Cette théorie sur la conduction dans les semi-conducteurs du type P peut sembler à première vue, artificielle et complexe : en réalité, elle permet une meilleure analogie pour représenter les 2 types de semi-conducteurs (P et N) et une explication plus simple des phénomènes sur lesquels est basé le fonctionnement des diodes et des transistors. Elle trouve aussi une base dans la mesure de l’effet HALL, d’après laquelle on montre qu’effectivement, un semi-conducteur du type P se comporte comme si le courant était constitué par des déplacements de charges positives et non par des charges négatives.

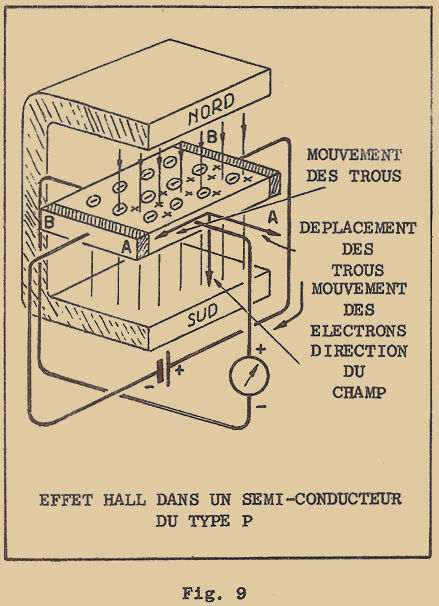
En fait, tandis que dans un semi-conducteur du type N, la tension due à l’effet Hall apparaît avec la même polarité que dans un conducteur métallique dans lequel le courant est formé par un flux d’électrons (voir leçon précédente), dans un semi-conducteur du type P on mesure une tension dont la polarité est inverse ; ce fait ne peut être expliqué que si l’on admet que les charges mobiles dans le semi-conducteur sont positives.

Il suffit de regarder la figure 9 pour remarquer que maintenant les charges mobiles sont positives et qu’elles se déplacent dans le champ magnétique vers la gauche dans le sens de déplacement des trous.

Mais le déplacement vers la gauche s’effectuant par rapport à la direction du mouvement, et comme ce mouvement est maintenant en sens inverse par rapport à celui des électrons, il en résulte que l’accumulation des charges est encore une fois sur le côté AA du semi-conducteur.

La tension qui apparaît doit donc être de polarité inverse par rapport à celle qui a été indiquée dans la leçon précédente, puisque les charges qui s’accumulent sont maintenant positives. Puisque l’expérience montre que la tension due à l’effet Hall a précisément cette polarité dans un semi-conducteur P, on en déduit que le courant qui y circule est constitué par des charges positives. Nous avons ainsi une confirmation expérimentale que les trous sont équivalents à des charges positives.

Comme dans les semi-conducteurs du type N, la conductibilité dépendait de la concentration et de la mobilité des électrons, dans les semi-conducteurs du type P elle dépend de la concentration et de la mobilité des trous. A concentration égale, la conductibilité des semi-conducteurs P est plus faible (c’est-à-dire que la résistivité est plus grande) que dans les semi-conducteurs N ; celle-ci dépend en effet de la mobilité des trous qui est plus faible que celle des électrons.

Dans le cas du germanium, la mobilité des trous est seulement la moitié de celle des électrons : l’explication peut se trouver dans le fait que le déplacement d’un trou correspond au déplacement de plusieurs électrons.

2 - CONDUCTION INTRINSÈQUE

Dans la leçon précédente, en étudiant les semi-conducteurs purs (c’est-à-dire non dopés), nous avons vu que le germanium et le silicium avaient une structure du réseau cristallin identique à celle du diamant, et qu’ils ne se comportaient pas comme d’excellents isolants, sauf à la température voisine du zéro absolu. Le fait de la conduction "intrinsèque" des semi-conducteurs, c’est-à-dire leur conduction propre et lorsqu’ils ne sont pas dopés, était alors attribuée à la présence d’électrons libres provenant de l’agitation thermique des atomes.

Maintenant que nous avons étudié comment la conduction pouvait provenir d’un mouvement de charges positives, représentées par des trous, nous pouvons revenir sur ce phénomène de la conduction intrinsèque et l’expliquer d’une façon beaucoup plus complète.

Prenons un bloc de germanium (ou de silicium) très pur, c’est-à-dire pratiquement sans aucune sorte d’impuretés et portons-le au zéro absolu (- 273°C) ; tous ses atomes sont alors parfaitement immobiles et tous les électrons sur leur orbite solidement liés à ceux-ci. Il n’y a pas de charges libres dans le cristal.

Élevons progressivement la température du bloc de germanium ; ses atomes vont commencer à vibrer et ce d’autant plus que la température sera plus élevée. De telles vibrations vont provoquer comme je vous l’ai déjà dit, la rupture de quelque liaisons : ceci signifie qu’un certain nombre d’atomes vont perdre un électron qui va se détacher de son orbite et, devenant libre, vagabonder dans le réseau cristallin.

Chaque électron qui quitte son orbite, laisse à sa place un trou. Nous pouvons donc dire, que chaque liaison qui se rompt, provoque la formation d’un couple ELECTRON-TROU, ce qui signifie, que nous obtenons une charge négative libre (électron) et une charge positive libre (trou) comme vous pouvez le voir sur la figure 10.

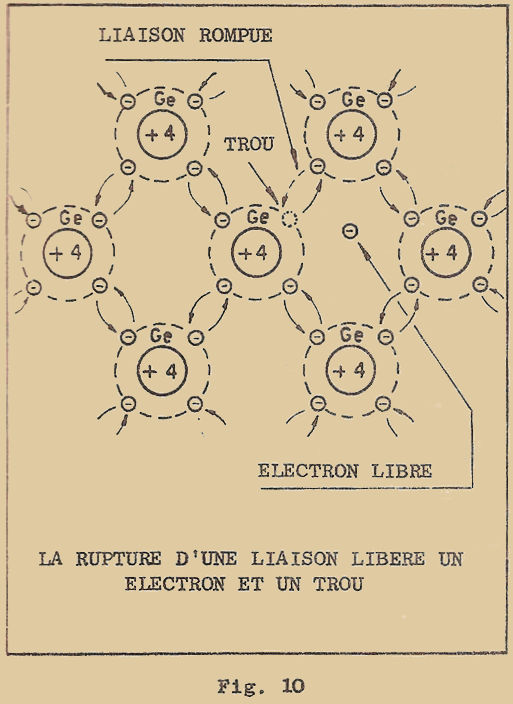
Les électrons et les trous ainsi libérés, vont vagabonder dans le germanium puisqu’aucune tension n’est appliquée et naturellement quand un électron va rencontrer un trou, ils vont se recombiner (l’électron "tombe" dans le trou) et le couple électron-trou va disparaître. En d’autres termes, un électron devenu libre, laisse à sa place un trou, et va voyager dans le cristal pour un temps extrêmement bref jusqu’à ce qu’il "tombe" dans un autre trou et perdre ainsi de nouveau sa liberté. Tandis qu’un électron jouit ainsi pendant un bref instant de sa liberté, ou si vous le préférez qu’il vit sa vie si brève, d’autres électrons "naissent" et "meurent".

Le phénomène est analogue à celui qui se produit dans une grande ville : tous les jours, naissent un certain nombre de personnes et en meurent un autre nombre presque égal, la population se maintenant presque constante. De même, dans le cristal de germanium, naissent et meurent continuellement des couples électron-trou. Ainsi, à chaque instant, il y a dans le cristal un certain nombre d’électrons et autant de trous qui "vivent", c’est-à-dire qu’il y a un certain nombre de charges négatives et de charges positives qui sont libres.

Le nombre de charges libres est d’autant plus élevé que plus grande est la température ; à la température ambiante (25° C) on calcule que dans 1 cm³ de germanium, il y a près de mille millions de millions d’électrons libres et autant de trous. Ce nombre peut paraître extrêmement grand, mais comme le nombre d’atomes de germanium dans 1 cm³ est beaucoup plus grand, il y a seulement un atome sur 50 millions qui possède un couple électron-trou. Le pourcentage des charges libres est très faible dans le germanium et encore plus dans le silicium ; pour cette raison, la conductibilité de tels semi-conducteurs, non dopés et à la température ambiante, n’est pas très élevée.

La conductibilité intrinsèque d’un semi-conducteur est due, non seulement aux électrons, comme je vous l’ai déjà dit dans la dernière leçon, mais aussi à un nombre égal de trous. Un bloc de semi-conducteur pur peut donc être représenté, du point de vue électrique, par un rectangle contenant un certain nombre de charges négatives libres (signe – dans la figure 11) et par un nombre égal de charges positives (signe + dans la même figure).

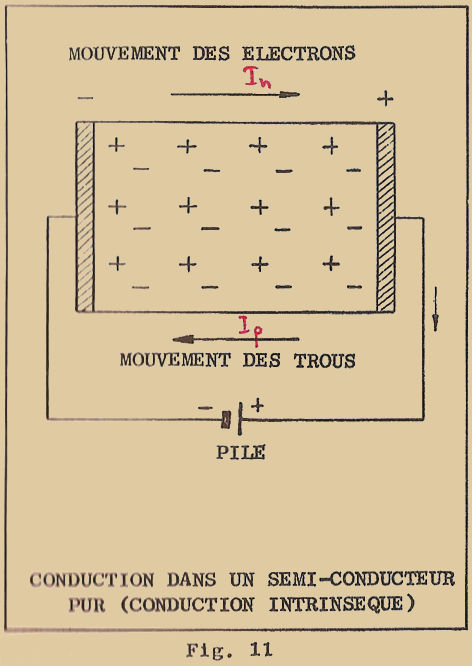
Si nous appliquons une tension à ce bloc de germanium, nous aurons en même temps à l’intérieur de celui-ci, un mouvement d’électrons de la gauche vers la droite (c’est-à-dire du – vers le +) et un mouvement de trous en sens contraire (de la droite vers la gauche, c’est-à-dire du + vers le -). À l’intérieur du germanium, le courant total délivré par la pile sera dû en partie à des électrons (courant électronique "négatif" I_n) et en partie à des trous (courant I_p). À cause de la mobilité différente des électrons et des trous dans le germanium, le courant I_n (courant dû aux électrons) sera environ le double de I_p (courant dû aux lacunes) ; on peut donc dire qu’à l’intérieur du germanium pur, le courant est dû pour deux tiers à des électrons et pour un tiers seulement aux trous, puisque ceux-ci sont plus lents.

3 – PORTEURS MAJORITAIRES ET MINORITAIRES

La faible conductibilité du germanium (ou du silicium) pur, dû aux couples électron-trou présents dans le réseau cristallin peut être notablement augmentée en introduisant un nombre plus ou moins grand d’impuretés. Comme nous l’avons vu, chaque atome introduit équivaut à l’introduction dans le cristal d’un électron libre (lorsque l’atome d’impureté est du type donneur) ou d’un trou (quand l’impureté est du type accepteur) ; le nombre d’atomes d’impuretés introduit est en général beaucoup plus grand que celui des couples électron-trou existants dans le cristal. La conductibilité due aux charges libres existantes peut donc être négligée en comparaison des charges libres introduites par le dopage. C’est pour cette raison, que lorsque l’on étudie la conduction dans un semi-conducteur dopé on peut dire que dans le germanium N, la conduction est due à des électrons, tandis que dans le germanium P elle est due à des lacunes et l’on peut représenter les 2 types de semi-conducteurs comme indiqué dans la figure 3 et la figure 6 respectivement.

En réalité, aussi, dans un semi-conducteur dopé, outre les charges libres que l’on introduit, il y a toujours celles dues aux couples électron-trou, bien que le nombre de ces couples se trouve réduit par le dopage même, toutes choses égales par ailleurs.

Si l’on voulait représenter de façon plus exacte un semi-conducteur dopé, on devrait tenir compte, outre les charges fixes (ions) et mobiles (électrons ou trous) qui correspondent à chacun des atomes d’impuretés introduits (donneur ou accepteur), des charges mobiles (électrons et trous) dues aux couples électron-trou qui sont, rappelons-le, en nombre infime par rapport aux premières.

Si, par exemple, on considère un bloc de germanium N, on devra le représenter comme sur la figure 3 en y adjoignant un certain nombre de couples électron-trou. La représentation complexe qui va en résulter sera celle de la figure 12-a où sont indiqués : des cercles avec le signe + qui représentent les ions des atomes donneurs ; un nombre égal de signes -, qui représentent les électrons, c’est-à-dire les charges négatives mobiles ; un petit nombre de couples électron-trou, représentés chacun par un signe + et un signe -. Les charges négatives résultantes sont donc celles dues aux ions donneurs plus les couples électron-trou.

Ce sont les charges négatives qui contribuent surtout à la conduction tandis que les charges positives contribuent elles, pour une très faible part car elles sont en nombre réduit. C’est pour cette raison, que les premières sont appelées Porteurs Majoritaires et les secondes Porteurs Minoritaires.

On peut représenter par analogie un semi-conducteur du type P (figure 12-b) ; on voit que la représentation est identique à celle de la figure 12-a dans laquelle on a permuté les signes + et -.

En conclusion, les propriétés des 2 types de semi-conducteurs peuvent être résumées par le tableau suivant :

TYPE DE SEMI-CONDUCTEURS	N	P
Charges fixes	ions positif	ions négatifs
Porteurs majoritaires	électrons (-)	trous (+)
Porteurs minoritaires	trous (+)	électrons (-)

Les porteurs minoritaires peuvent être négligés quand on considère la conduction dans un simple conducteur dopé, mais revêtent une importance capitale dans l’étude des diodes et des transistors.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 3^ème LEÇON THÉORIQUE

1 – L’aptitude d’un matériau à bien conduire le courant électrique dépend exclusivement des électrons périphériques de ses atomes.

2 – Du point de vue électrique, on peut représenter un atome de façon simplifiée comme un ion fixe ayant autant de charges positives qu’il y a d’électrons périphériques et entouré d’autant de charges négatives mobiles.

3 – La résistivité d’un conducteur dépend du nombre d’électrons libres dans celui-ci et de leur mobilité.

4 – Quand on élève la température d’un conducteur, sa résistivité augmente, parce que les atomes vibrent de plus en plus fort et gênent de plus en plus le flux d’électrons.

5 – La conductibilité d’un matériau est son aptitude plus ou moins grande à conduire le courant ; elle s’exprime en siemens par centimètre (S/cm).

6 – Le diamant se comporte comme un isolant parfait car il possède des liaisons de valence extrêmement solides, qui maintiennent les électrons périphériques solidement liés aux noyaux. Il n’en est pas de même en ce qui concerne le germanium, présentant des liaisons plus faibles qui peuvent se rompre facilement.

7 – La résistivité d’un semi-conducteur diminue lorsque l’on fait croître la température, parce que plus celle-ci est élevée, plus il y a d’électrons libérés par rupture d’un plus grand nombre de liaisons.

8 – Si un conducteur et un semi-conducteur pouvaient être portés à la température de 0° K, la résistivité du premier deviendrait pratiquement nulle – les atomes s’immobilisant complètement ne feraient plus d’obstacle au flux d’électrons -, tandis que la résistivité du second serait infiniment grande, puisqu’il n’y aurait plus de liaisons rompues et qu’ainsi il n’y aurait plus d’électrons libres.

9 – L’effet Hall consiste en l’apparition d’une faible tension entre les deux faces latérales d’un conducteur quand celui-ci est parcouru par un courant et soumis à l’action d’un champ magnétique transversal.

---

EXERCICES DE RÉVISION SUR LA 4^ème LEÇON THÉORIQUE

1 – Qu’appelle-t-on "doper" un semi-conducteur  ?

2 – Quels sont les atomes qui prennent le nom de DONNEURS et d’ACCEPTEURS et pourquoi  ?

3 – Qu’entend-t-on par concentration et mobilité des électrons dans un semi-conducteur  ?

4 – Quelle différence y a-t’ il entre un semi-conducteur du type N et un semi-conducteur du type P  ?

5 – Qu’appelle-t-on un "trou"  ?

6 – Dans quelle direction se déplacent les trous par rapport aux électrons  ?

7 – Qu’entend-on par couple électron-trou et comment est-il produit  ?

8 – Qu’appelle-t-on conduction intrinsèque d’un semi-conducteur et à quoi est-elle due  ?

9 – A concentration égale de porteurs, la conductibilité est-elle plus grande dans un semi-conducteur du type N ou dans celui du type P et pourquoi  ?

Fin de la leçon 4

---

LECON 5

Dans la leçon précédente, nous avons étudié le phénomène de la conduction dans un semi-conducteur "intrinsèque", c’est-à-dire pur, et "dopé" avec des impuretés pentavalentes (atomes "donneurs") ou trivalentes (atomes "accepteurs").

Nous avons vu aussi, que dans le cas d’un semi-conducteur intrinsèque, la conduction avait lieu par déplacement d’électrons (charges négatives) du côté du germanium relié au pôle négatif de la pile vers celui qui était relié au pôle positif, et en même temps, par déplacement en sens inverse des trous (c’est-à-dire du pôle positif vers le pôle négatif).

Dans le cas d’un semi-conducteur dopé, le phénomène est encore à peu près le même, sauf en ce qui concerne un nombre plus grand de charges positives et négatives mises en jeu et l’on a en outre une majorité d’un des types de charges par rapport à l’autre. Pour cette raison, la conduction est due surtout à un seul type de charge, et précisément à des charges négatives dans un semi-conducteur du type N et à des charges positives dans un semi-conducteur du type P. Dans le premier cas, les électrons constituent les porteurs majoritaires et les trous, les porteurs minoritaires ; dans le second cas, au contraire, les porteurs majoritaires sont constitués par des trous et les porteurs minoritaires par des électrons.

Nous allons voir maintenant, ce qui se passe lorsque 2 blocs de semi-conducteurs, l’un du type P et l’autre du type N, sont mis au contact l’un de l’autre pour former ce que l’on appelle une JONCTION P-N. Pour mieux comprendre le comportement d’une telle jonction, il est préférable que je vous décrive brièvement une expérience très simple que vous pouvez réaliser facilement.

Prenons un récipient en verre transparent qui peut être divisé en deux parties égales par l’intermédiaire d’une cloison poreuse. On utilisera pour cette expérience un verre ordinaire, la cloison peut être réalisée à l’aide d’une feuille de carton, d’un papier épais, ou d’un autre matériau, pourvu que celui-ci ne soit pas imperméable. Ce papier devra être découpé aux dimensions exactes du verre et il sera collé à l’intérieur à l’aide d’une colle qui une fois sèche ne se dissout pas dans l’eau. Il faut vérifier aussi qu’une fois la "soudure" cloison-verre faite, celle-ci est parfaite, de telle sorte qu’il n’y ait aucune possibilité de passage du liquide par les "côtés".

Remplissons maintenant les 2 demi-récipients avec de l’eau, et mettons une goutte d’encre rouge dans l’un et une goutte d’encre bleue dans l’autre ; on obtient ainsi 2 liquides colorés repérés par R (rouge) et B (bleu).

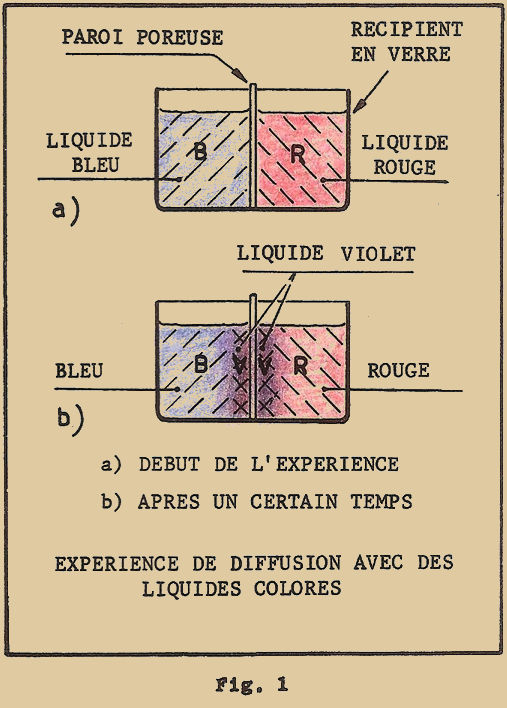
Nous obtenons ainsi la configuration de la figure 1-a, avec le liquide rouge d’un côté et le liquide bleu de l’autre. Laissons les 2 liquides immobiles sans les agiter ; au bout d’un certain moment, de part et d’autre de la cloison, nous verrons apparaître un liquide violacé, repéré par V sur la figure 1-b qui va augmenter de plus en plus en largeur.

La formation de cette zone violacée est due à un fait très simple : les 2 liquides paraissent être immobiles, mais en réalité sont animés d’une agitation moléculaire continuelle, ce qui fait qu’au travers de la paroi poreuse, ils passent de l’un à l’autre et finissent par se mélanger.

La rapidité de diffusion des 2 liquides au travers de la paroi est maximum au début du phénomène, puis va en diminuant progressivement, jusqu’à cesser complètement lorsque les 2 liquides ont fini par se mélanger intimement, en prenant une teinte uniforme.

Si nous revenons aux semi-conducteurs dopés P et N, nous pouvons avoir un phénomène analogue aux 2 liquides colorés : l’eau pure pourra être considérée comme l’équivalent du germanium pur, les encres rouge et bleue correspondant aux impuretés pentavalentes et trivalentes.

1 – 1 FORMATION DE LA BARRIÈRE DE POTENTIEL

Considérons 2 blocs de germanium, un du type P et l’autre du type N : nous pouvons les représenter, comme nous l’avons déjà vu dans la leçon précédente et que je vous rappelle à la figure 2-a

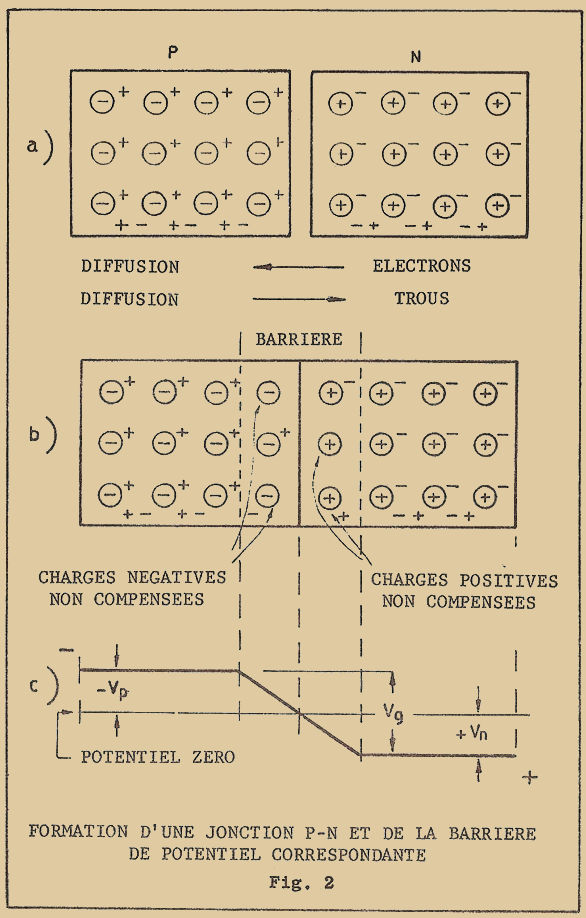
Le germanium P sera représenté par des cercles avec le signe – qui indique que ce sont les ions négatifs des atomes accepteurs ; les signes + représentent les porteurs majoritaires constitués par les trous, et enfin quelques signes – qui représentent les porteurs minoritaires constitués par des électrons. Pour le germanium N, nous aurons au contraire, des cercles renfermant le signe + et qui représentent les ions positifs des atomes donneurs, les signes – qui représentent les porteurs majoritaires constitués par des électrons et les signes + qui représentent les porteurs minoritaires constitués par des trous.

Mettons en contact les 2 blocs de germanium comme indiqué sur la figure 2-b. Il se produit un phénomène analogue à celui que nous avons vérifié dans l’expérience décrite précédemment. Comme tout à l’heure, avec la diffusion des 2 liquides d’une paroi à l’autre, les charges libres des 2 germaniums vont commencer à diffuser à travers la jonction d’un bloc dans l’autre.

Ainsi, les électrons du germanium N (nous ne considérons pour le moment que les porteurs majoritaires) vont traverser la jonction et diffuser dans le germanium P, où ils vont se recombiner avec les trous ; de leur côté, les trous du germanium P franchissent la jonction, diffusent dans le germanium N et se recombinent avec des électrons. Tandis que dans le cas des liquides colorés, le phénomène continue jusqu’à ce qu’ils se soient complètement mélangés, dans le cas du germanium le phénomène s’arrête rapidement et ne continue plus comme on pourrait le penser au premier abord.

Si nous regardons de plus près ce qui se passe autour de la jonction, c’est-à-dire au voisinage de la limite de contact entre 2 blocs (figure 2-b), nous pouvons voir qu’en ces régions, la concentration des charges mobiles diminue pour deux raisons, bien distinctes : tout d’abord à cause de la diffusion, puisqu’une partie des électrons du germanium N passe dans le germanium P et, inversement une partie des trous du germanium P passe dans le germanium N.

Ensuite à cause de la recombinaison, puisqu’une autre partie des électrons du germanium N se recombine avec des trous provenant du germanium P et, inversement une partie des trous du germanium P se recombine avec des électrons du germanium N.

Il résulte de cela, que dans le voisinage immédiat de la zone de jonction entre les 2 types de germanium, les charges fixes des ions donneurs et accepteurs ne sont plus toutes neutralisées par les charges mobiles de signe contraire. Dans la région P alors, comme vous pouvez le constater sur la figure 2-b, le nombre des charges mobiles positives ne sera plus égal à celui des charges fixes négatives, mais sera devenu inférieur, c’est-à-dire que l’on aura un certain nombre de charges négatives non compensées : de même dans la région N nous aurons une déficience d’électrons et il y aura donc un certain nombre de charges fixes positives non compensées.

Les 2 blocs de germanium, qui au début étaient électriquement neutres, maintenant ne le sont plus ; la région P va se charger négativement par la présence des charges négatives fixes qui ne sont plus neutralisées par les charges positives mobiles ; la région N va se charger positivement par la présence des charges positives fixes qui ne sont plus compensées par les charges négatives mobiles.

A cause de ces charges non compensées, les deux régions vont se charger à des potentiels respectivement négatif et positif par rapport à la valeur zéro qu’elles avaient avant la jonction ; entre les deux régions apparait maintenant une différence de potentiel V_g. Le passage du potentiel négatif – V_p (celui de la région P) au potentiel positif + V_n (celui de la région N) est graduel et occupe toute la zone de jonction est appelée BARRIÈRE, c’est-à-dire la zone où se trouvent les charges non compensées, comme vous pouvez le voir sur la figure 2-c.

Il est évident que cette différence de potentiel, nulle à l’instant où les 2 régions sont mises en contact, va augmenter continuellement au fur et à mesure que les charges libres diffusent d’une région à l’autre et se neutralisent mutuellement, car le nombre de charges non compensées va croître.

Mais la différence de potentiel qui apparait dans la zone de la jonction a une polarité telle qu’elle s’oppose à la diffusion des charges libres ; elle va croître donc jusqu’au moment où devenue suffisamment élevée, elle va empêcher une diffusion ultérieure des charges libres. Pour cette raison, la différence de potentiel de la jonction prend le nom de BARRIÈRE DE POTENTIEL, puisqu’elle constitue un obstacle à la diffusion ultérieure des charges.

1 – 2 ÉQUILIBRE DYNAMIQUE DE LA JONCTION

Pour étudier de plus près le phénomène, on peut avoir recours comme toujours, à une analogie du type mécanique. Les deux semi-conducteurs peuvent être représentés par deux plans, disposés sur un même niveau lorsqu’ils sont au même potentiel et sur des niveaux différents s’il existe une différence de potentiel entr’eux. Dans ce cas, la différence de niveaux entre les deux plans sera d’autant plus grande que l’est la différence de potentiel. Le plan qui représente le semi-conducteur P sera placé le plus haut. Les électrons pourront être représentés par des boules noires lourdes posées sur les plans et qui tendent à rouler vers le bas (parce qu’elles sont lourdes). Les trous, au contraire, pourront être représentés par des boules blanches très légères qui tendent à monter et qui sont disposées sous les plans comme le feraient des ballons que l’on vend dans les fêtes, et qui libérés vont se "coller" au plafond.

La représentation complexe de la jonction sera celle de la figure 3. Sur le plan de droite, disposé vers le bas (semi-conducteur N à potentiel positif) on trouve autant de boules noires qu’il y a de porteurs majoritaires (constitués par des électrons) et sous le plan, il y a quelques boules blanches (porteurs minoritaires constitués par des trous) ; sur le plan de gauche, disposé vers le haut, (semi-conducteur P à potentiel négatif), on trouve au contraire très peu de boules noires (porteurs minoritaires, constitués par des électrons) et dessous, autant de boules blanches qu’il y a de porteurs majoritaires (constitués par les trous). Les 2 plans horizontaux sont reliés par un plan incliné qui représente la barrière de potentiel de la jonction.

En se rappelant en outre, qu’à cause de l’agitation thermique toutes les boules sont en mouvement désordonné continuel, il est facile de prévoir ce qui peut arriver dans les conditions de la figure 3.

Les boules noires de droite, dans leur mouvement vont se trouver au pied de la barrière et vont tenter de la franchir : seules quelques-unes d’entr’elles possédant une énergie suffisante pourront atteindre le sommet, tandis que les autres arrivées à une certaine hauteur, vont redescendre. Les boules noires de gauche, qui vont se trouver près de la pente vont rouler vers le bas et se trouver sur le plan de droite.

Pour les boules blanches, le même phénomène va se produire : celles de gauche dans leur mouvement vont chercher à descendre le long de la barrière, mais toutes n’y réussiront pas. Tandis que celles de droite, dès qu’elles vont atteindre le plan incliné, vont glisser vers le haut, et rejoindre les boules de gauche.

En conclusion, l’effet de la barrière est de favoriser le passage de la gauche vers la droite des boules noires et de la droite vers la gauche des boules blanches. Mais par contre, la barrière fait office d’obstacle pour le passage inverse, c’est-à-dire des boules noires de droite vers la gauche et des boules blanches de gauche vers la droite.

Cependant, les boules noires de gauches et les boules blanches de droite représentent les porteurs minoritaires, tandis que les boules noires de droite et les boules blanches de gauche représentent les porteurs majoritaires : on peut donc en conclure, que la barrière de potentiel favorise le passage au travers de la jonction des porteurs minoritaires et fait office d’obstacle au passage des porteurs majoritaires.

Le phénomène peut donc être résumé de la façon suivante. Dès que les deux semi-conducteurs sont mis en contact, il y a diffusion des porteurs majoritaires de l’un vers l’autre au travers de la jonction, et début de formation de la barrière de potentiel à cause des charges fixes qui restent et qui ne sont plus compensées.

La diffusion des porteurs majoritaires détermine un courant (à qui on donne, comme nous le verrons par la suite, le nom de "courant direct") à travers la jonction, constitué par le flux F_n d’électrons de droite vers la gauche et par le flux F_p de trous de la gauche vers la droite.

Ces deux flux diminuent au fur et à mesure que la barrière de potentiel croît, et si les porteurs minoritaires n’avaient pas existé, la barrière de potentiel aurait augmenté jusqu’au moment où F_n et F_p seraient devenus nuls (figure 3).

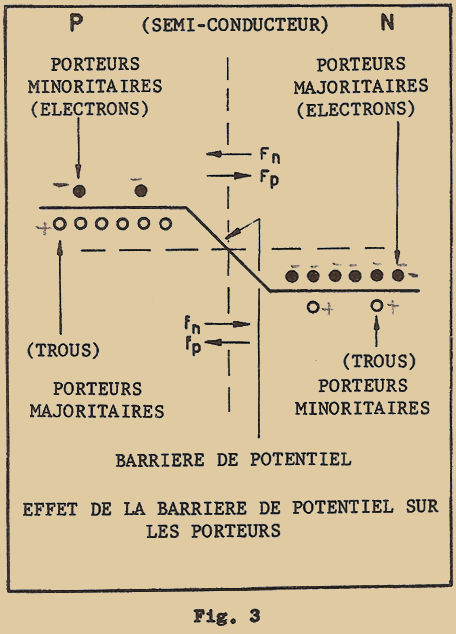
Mais en réalité, il existe des porteurs minoritaires et nous avons vu qu’ils sont sollicités par la pente de la barrière de potentiel à traverser la jonction. Ainsi, dès que la barrière de potentiel commence à se former, tous les porteurs minoritaires qui se trouvent au voisinage de la jonction sont attirés de l’autre côté de la jonction. À travers la jonction, s’établit donc un courant de porteurs minoritaires auquel on donne le nom de "courant inverse", et il en résulte un flux d’électrons f_n de gauche vers la droite et un flux de lacunes f_p de droite vers la gauche (figure 3) dont l’intensité ne dépend pratiquement pas de l’amplitude de la barrière de potentiel, mais seulement de la quantité de porteurs minoritaires présents dans les semi-conducteurs.

Ainsi la barrière de potentiel n’augmentera pas jusqu’à annuler complètement les flux des porteurs majoritaires, mais seulement jusqu’à les réduire et les rendre exactement égaux aux flux des porteurs minoritaires.

La condition de régime sera atteinte (c’est-à-dire qu’alors le courant complexe à travers la jonction sera nul) quand les flux f_n et f_p des porteurs minoritaires seront exactement compensés par les flux en sens inverse des porteurs majoritaires F_n et F_p. En d’autres termes, ce sera au moment où il y aura autant d’électrons qui passeront de gauche vers la droite (f_n) que d’électrons qui passeront de droite vers la gauche (F_n) et qu’il y aura autant de trous qui passeront de droite vers la gauche (f_p) que de trous de la gauche vers la droite (F_p). De façon complexe, tout se passe comme si aucun électron, ni aucun trou, ne traversaient la jonction ; on dit alors que la jonction a atteint un régime d’équilibre dynamique.

1 – 3 HAUTEUR DE LA BARRIÈRE DE POTENTIEL

La hauteur de la barrière de potentiel doit être telle qu’elle rende parfaitement égaux (de façon qu’ils se neutralisent au voisinage) les flux des porteurs majoritaires et minoritaires à travers la jonction.

Pour déterminer la valeur en volt de la barrière de potentiel qui s’établit au voisinage des deux semi-conducteurs, il faut encore tenir compte de l’aspect suivant du phénomène.

Si nous revenons à notre analogie mécanique de la figure 3, nous pourrons en déduire que la barrière de potentiel sera d’autant plus élevée, que seront grandes les énergies des porteurs majoritaires, car ils pourront la sauter plus facilement. Mais la vitesse des porteurs (ou l’énergie) dépend uniquement de la température à laquelle se trouve le semi-conducteur ; ainsi la hauteur de la barrière de potentiel dépend elle aussi de la température et croît avec cette dernière.

A la température ambiante (27°C ou 300°K), la valeur calculée de la hauteur de la barrière de potentiel est de l’ordre de 0,3 V pour une jonction de deux semi-conducteurs au germanium et de 0,7 V pour une jonction obtenue avec deux semi-conducteurs au silicium.

Remarquez bien, que je dis "valeur calculée" et non pas "valeur mesurée" car il n’est pas possible de mesurer à l’aide d’un voltmètre la hauteur de la barrière de potentiel.

En effet, si l’on désirait mesurer une telle différence de potentiel à l’aide d’un voltmètre, on brancherait les pointes de touche de l’appareil aux deux extrémités des semi-conducteurs qui forment la jonction P-N directement ou à travers des armatures métalliques comme indiqué sur la figure 4-a. Mais entre l’armature A et le semi-conducteur P apparait une tension et de même entre l’armature B et le semi-conducteur N et ces deux tensions sont telles qu’elles ramènent des deux armatures (elles sont faites dans le même métal) au même potentiel.

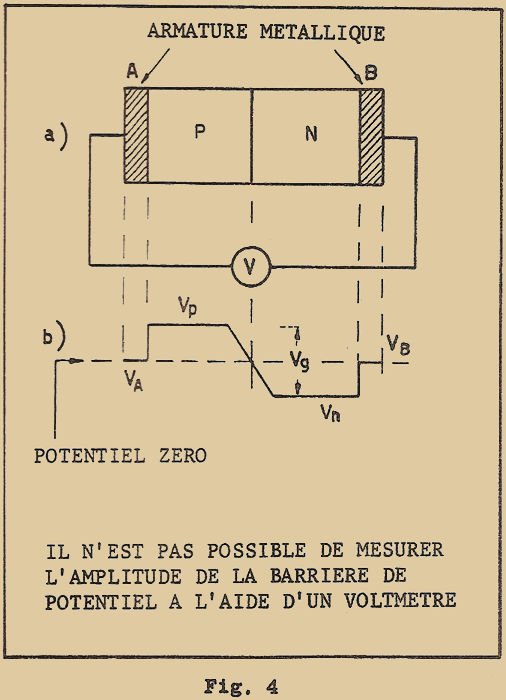
Si l’on représente les potentiels des deux semi-conducteurs et des armatures métalliques, on obtient le graphique de la figure 4-b où l’on voit que V_A et V_B se trouvent exactement au même niveau : ainsi si l’on branche entre eux un voltmètre, l’appareil ne peut indiquer de tension.

L’explication du phénomène peut aussi être donnée en raisonnant en énergie. Si l’appareil de mesure indiquait une tension, cela voudrait dire que dans le circuit il circule un certain courant et qu’ainsi la jonction fournit une énergie électrique, sans qu’on lui fournisse une énergie équivalente de quelque nature que ce soit ; en effet, à l’intérieur de la jonction, on ne constate aucun phénomène chimique qui délivrerait de l’énergie électrique (comme cela se produit dans une pile) ; on ne lui fournit pas non plus de l’énergie thermique (comme dans les piles solaires) ni de l’énergie mécanique (comme dans les dynamos ou dans les alternateurs) et il ne s’y produit pas non plus de phénomène de désintégration atomique (comme cela se produit dans la pile atomique).

On devrait alors conclure que la jonction "crée" de l’énergie à partir de rien : ceci ne peut avoir lieu car ce serait contraire au principe qui dit que rien ne se crée, rien ne se détruit (principe de la conservation de l’énergie)

On doit donc admettre que la différence de potentiel qui apparait entre les armatures métalliques et les semi-conducteurs est de sens tel qu’elle compense exactement la barrière de potentiel de la jonction.

Il faut remarquer encore qu’il n’y a aucune "astuce" qui permette de mesurer la tension de la jonction. On pourrait penser par exemple à ne pas mettre d’armatures A et B, et brancher directement les pointes de touche du voltmètre sur les faces externes des semi-conducteurs : la tension qui compenserait la barrière de potentiel se formerait alors directement entre les pointes de touche et le semi-conducteur. On pourrait penser aussi, utiliser des armatures en métal différent : dans ce cas, effectivement, les potentiels V_A et V_B ne seront plus égaux, mais lorsque l’on branchera sur les armatures les pointes de touche du voltmètre, il apparaîtra entre les pointes de touche et les armatures d’autres tensions par effet Volta (potentiel de "contact" remarqué déjà par les électrotechniciens du siècle dernier), qui compenseront à leur tour la différence de potentiel existant entre A et B.

2 – POLARISATION DE LA JONCTION

Après avoir examiné comment était formée une jonction et comment elle se comportait en l’absence de tension appliquée à ses extrémités, il faut que nous étudiions son comportement lorsqu’elle vient à être polarisée, c’est-à-dire lorsque l’on applique à ses bornes une tension de valeur donnée ; en d’autres termes, nous allons étudier le phénomène de la conduction au travers de la jonction.

Étant donné que la jonction est formée par la juxtaposition d’un semi-conducteur P et d’un semi-conducteur N, nous voyons immédiatement qu’il peut y avoir deux cas distincts de branchement d’une pile, selon que le pôle positif de celle-ci est relié au semi-conducteur N ou au contraire au semi-conducteur P.

Dans le premier cas, je vous ai illustré à la figure 5-a, le pôle positif de la pile est réuni à l’armature métallique B placée sur le semi-conducteur N et le pôle négatif est relié à l’armature A, du côté du semi-conducteur P : de cette manière, le semi-conducteur P est polarisé négativement par rapport au semi-conducteur N.

Si vous vous rappelez qu’à cause de la formation de la barrière de potentiel, le semi-conducteur P se trouvait déjà porté à un potentiel négatif par rapport au semi-conducteur N avant même que l’on n’applique une tension extérieure quelconque, vous en déduisez immédiatement qu’étant donné que la tension de la pile a la même polarité que la barrière de potentiel, la hauteur de celle-ci sera augmentée.

Ce qui vient d’être dit, peut-être vérifié en examinant le diagramme qui représente les potentiels de la jonction quand aucune tension n’est appliquée, les armatures A et B se trouvent au même potentiel, c’est-à-dire que V_A et V_B sont sur un même niveau, tandis que le semi-conducteur P se trouve à un potentiel négatif et le semi-conducteur N à un potentiel positif (représenté par la ligne en pointillés sur la figure 5b) : ces potentiels se trouvent respectivement au-dessus et en-dessous de la ligne horizontale de référence (potentiel zéro).

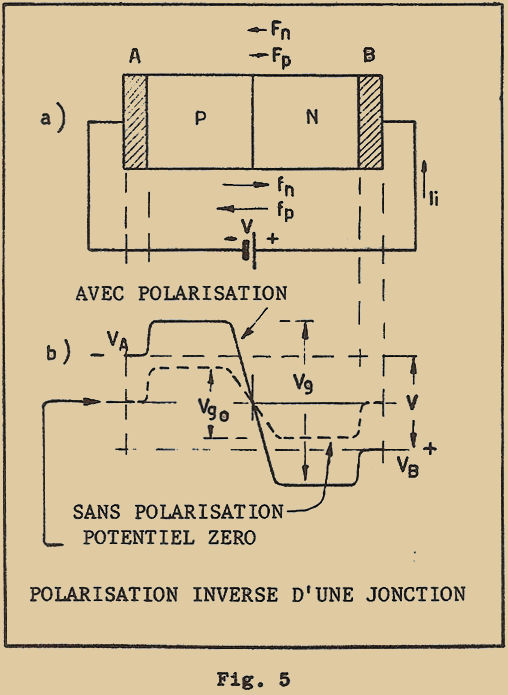
Appliquer une tension V aux armatures A et B signifie porter V_A et V_B à une différence de niveau égale à la valeur V ; comme le pôle négatif de la pile est relié à l’armature A et que le pôle positif est relié à l’armature B, V_A se déplace vers le haut et V_B vers le bas : par conséquent, la hauteur de la barrière de potentiel qui initialement avait la valeur V_g0 se déplacera à la valeur V_g égale à V_g0 + V. On peut déduire très facilement les effets que va provoquer la hauteur de la barrière de potentiel en se rappelant qu’elle est sans influence sur les flux des porteurs minoritaires, tandis que son effet est déterminant sur les flux des porteurs majoritaires. Nous pourrons donc prévoir que les flux f_p et f_n continueront à maintenir la même intensité qu’avant l’application de la tension, tandis que les flux F_n et F_p seront réduits et même annulés complètement si la barrière de potentiel atteint une hauteur suffisante pour empêcher complètement le passage des porteurs majoritaires au travers de la jonction.

L’équilibre dynamique de la jonction est ainsi rompu : les flux F_n et F_p, réduits ou même annulés, ne peuvent plus compenser les flux de sens inverse f_n et f_p ; il n’y aura effectivement passage au travers de la jonction que de trous de droite vers la gauche et d’électrons de gauche vers la droite c’est-à-dire d’un courant de porteurs minoritaires.

L’intensité d’un tel courant est très faible, car les porteurs minoritaires sont très peu nombreux et leur nombre ne dépend pas de la valeur de la tension appliquée, mais uniquement de la température à laquelle est portée la jonction ; de façon plus précise l’intensité augmente avec la température, car avec cette élévation croît le nombre de porteurs minoritaires existant dans chacune des régions du semi-conducteur, ainsi que les flux f_n et f_p.

En d’autres termes, nous pouvons dire qu’en polarisant la jonction comme indiqué à la figure 5, celle-ci va conduire très peu, c’est-à-dire qu’elle va présenter une résistance très élevée.

Inversons maintenant les connexions de la pile et portons ainsi, le semi-conducteur P à un potentiel positif, le semi-conducteur N à un potentiel négatif (figure 6-a). Si nous reprenons le raisonnement de tout à l’heure, il est facile de voir que la polarité de la tension appliquée est maintenant de sens opposé à celle de la barrière de potentiel. L’allure de la distribution des potentiels devient celle qui est indiquée en traits pleins sur la figure 6-b – (je vous ai représenté en lignes pointillés, le potentiel de la barrière avant la polarisation). La hauteur (ou l’amplitude) de la barrière de potentiel passe de la hauteur V_g0 à une valeur plus faible : V_g0 – V.

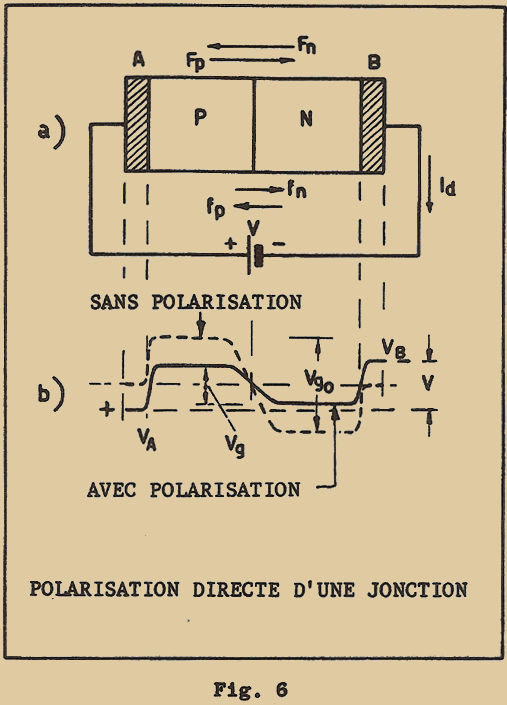
Les flux f_p et f_n des porteurs minoritaires gardent encore la même intensité, mais les flux F_p et F_n des porteurs majoritaires deviennent beaucoup plus grands, puisque la barrière de potentiel s’oppose moins au passage de ceux-ci. Maintenant ce sont les flux des porteurs majoritaires qui sont les plus importants et il y a effectivement passage d’électrons de droite vers la gauche et de trous de gauche vers la droite. Le courant qui traverse la jonction dépend de la hauteur de la barrière de potentiel puisque celle-ci règle les flux des porteurs majoritaires et il peut atteindre des valeurs élevées car les porteurs majoritaires sont en nombre élevé aussi. En d’autres termes, nous pouvons dire que si nous polarisons la jonction comme il est indiqué sur la figure 6, nous aurons une conduction élevée, c’est-à-dire que la jonction présente une résistance très faible.

En conclusion, une jonction P-N se comporte de façon différente selon la polarité de la tension qu’on lui applique : la jonction conduit bien, si le pôle positif de la pile est relié au semi-conducteur P et ne conduit pas (ou plus précisément conduit très peu) si le semi-conducteur P est relié au pôle négatif de la pile. Ce comportement est exactement celui d’une diode et l’on en déduit donc que la jonction P-N présente la même propriété de redressement qu’une diode.

Par analogie avec les diodes nous dirons que dans le cas de la figure 5, la jonction est polarisée en sens inverse et que le courant I_i qui traverse le circuit est d’intensité très faible, puisqu’il est constitué de porteurs minoritaires : ce courant est dit INVERSE.

Dans le cas de la figure 6, nous dirons que la jonction est polarisée dans le sens direct et que le courant I_d, d’intensité beaucoup plus grande car il est constitué par des porteurs majoritaires, est appelé DIRECT.

L’effet diode qui se manifeste dans une jonction P-N peut encore être expliqué d’une façon beaucoup plus simple, mais moins exacte, en considérant uniquement les porteurs majoritaires et en négligeant complètement les porteurs minoritaires comme nous l’avons fait au début de l’étude sur la conduction des semi-conducteurs dopés.

En polarisant la jonction en sens inverse, l’armature A se trouve portée à un potentiel négatif et l’armature B à un potentiel positif.

L’action d’une telle polarité est d’attirer les trous du semi-conducteur P vers l’armature A et les électrons du semi-conducteur N vers l’armature B comme sur la figure 7-a où pour simplifier le dessin, je ne vous ai représenté que les porteurs majoritaires en négligeant aussi les charges fixes des ions accepteurs et donneurs.

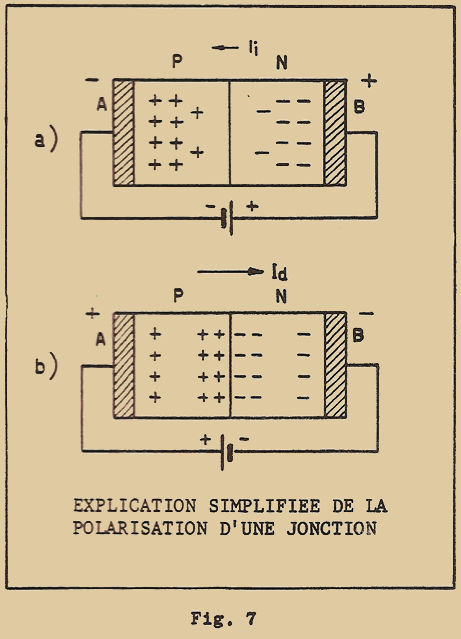
Dans ces conditions, nous avons un éloignement des trous et des électrons de la jonction et une interdiction faite à ceux-ci de traverser la jonction pour se recombiner entr’eux. Seuls quelques rares porteurs réussissent à traverser la jonction et le courant inverse I_i qui en résulte est très faible.

Dans le cas de la polarisation directe au contraire, le potentiel de l’armature A est positif et ainsi repousse les charges positives (trous) vers la jonction ; le même phénomène a lieu pour les électrons du semi-conducteur N qui sont repoussés vers la jonction par le potentiel négatif de l’armature B.

Les porteurs sont ainsi sollicités à traverser la jonction et à se recombiner et provoquent un courant direct I_d intense (figure 7-b).

Il faut remarquer encore, que les sens des courants direct et inverse de la figure 7 sont indiqués selon le système conventionnel c’est-à-dire que le courant se déplace du pôle positif vers le pôle négatif de la pile. En réalité, ce n’est que dans le semi-conducteur P seulement que les porteurs, constitués par des trous (charges positives), se déplacent dans le sens de la flèche, c’est-à-dire du pôle positif au pôle négatif. Dans le reste du circuit (semi-conducteur N, conducteurs métalliques de liaison avec la pile) le courant est constitué par des électrons (charges négatives) et pour lesquels, le véritable sens de déplacement des porteurs est opposé à celui de la flèche, c’est-à-dire qu’il va du pôle négatif de la pile au pôle positif.

Considérer que le flux du courant est dans un sens ou dans l’autre, n’a aucune importance, car il suffit de s’entendre sur les termes. Il suffit de rappeler que le sens conventionnel du courant est " du + vers le –" ; le sens électronique du courant (c’est-à-dire le sens de déplacement des électrons) est "du – vers le +" : raisonnez sur le véritable courant électronique (flux d’électrons) à l’intérieur d’une triode qui va bien du – (cathode émissive) au + (plaque).

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 4^ème LEÇON THÉORIQUE

1 – "Doper" un semi-conducteur signifie que l’on introduit des impuretés dans son réseau cristallin.

2 – On appelle donneurs les atomes des éléments pentavalents qui utilisés comme impuretés, donnent chacun un électron au semi-conducteur. On appelle accepteurs les atomes des éléments trivalents qui eux capturent chacun un électron du semi-conducteur.

3 – On appelle concentration des électrons dans un semi-conducteur le nombre d’électrons libres dans 1 cm³ de celui-ci : on appelle mobilité des électrons, la liberté de mouvement que ces électrons possèdent dans le réseau cristallin.

4 – La différence qui existe entre un semi-conducteur N et un du type P réside dans le type de charges libres qui y sont présentes : dans le premier cas, la conduction est due à des charges négatives, dans le second à des charges positives.

5 – On appelle "trou" (ou "lacune") l’absence d’un électron dans le réseau cristallin d’un semi-conducteur.

6 – Les trous se comportent comme des charges positives et se déplacent donc dans le sens opposé à celui des électrons.

7 – Par couple électron-trou on indique l’ensemble d’un électron devenu libre et du trou laissé par celui-ci dans le réseau ; l’apparition d’un tel couple est due à la rupture d’une liaison existant entre les atomes des semi-conducteurs.

8 – La conduction intrinsèque d’un semi-conducteur est sa conduction propre, c’est-à-dire lorsqu’il n’est pas dopé. Cette conduction est due à la présence d’un couple électron-trou.

9 – A égalité de concentration de porteurs, la conductibilité d’un semi-conducteur N est plus grande à cause de la plus grande mobilité des électrons.

---

EXERCICES DE RÉVISION SUR LA 5^ème LEÇON THÉORIQUE

1 – Par quelle réunion la jonction P-N est-elle formée  ?

2 – A quoi est due l’apparition de la barrière de potentiel  ?

3 – Jusqu’à quel moment la barrière de potentiel peut-elle croître  ? (explication simplifiée).

4 – Quelles sont les valeurs en volts de la hauteur de la barrière de potentiel dans le cas d’une jonction au germanium et au silicium  ? Comment mesure-t-on de telles valeurs  ?

5 – Quel est le comportement de la barrière de potentiel vis-à-vis des porteurs majoritaires et minoritaires existant dans les deux régions du semi-conducteur  ?

6 – Si l’on réunit les deux extrémités d’une jonction P-N non polarisée, quel est le sens du courant et pourquoi

7 – Pourquoi une jonction P-N se comporte-t-elle comme une diode  ?

8 – Le courant inverse d’une jonction varie comme la température de la jonction ; pourquoi  ?

9 – Par quoi le courant direct d’une jonction est-il constitué  ?

Fin de la leçon 5

---

LECON 6

1 – LA DIODE À JONCTION

Dans la leçon précédente, nous avons vu pourquoi une jonction P-N présentait les propriétés d’une diode, c’est-à-dire qu’elle conduisait bien le courant dans un sens et très mal dans le sens inverse ; de façon bien précise, nous avons démontré que la jonction conduisait quand elle était polarisée de telle sorte que la région P soit rendue positive par rapport à la région N ; ainsi en admettant que le courant circule dans le sens conventionnel nous dirons qu’il y a conduction dans le sens P-N et qu’il n’y a pas conduction dans le sens N-P.

La jonction P-N qui peut être formée avec du germanium ou du silicium, peut donc être utilisée comme une diode et par exemple redresser un courant alternatif. Le dispositif prend alors le nom de diode à jonction et son symbole graphique est celui de la pointe d’une flèche, appuyant sur un plan (figure 1). Le sens de la flèche indique le sens dans lequel la diode conduit, lorsque celle-ci est polarisée dans le sens direct, c’est-à-dire quand le pôle positif de la pile est relié du côté de la flèche. Pour bien le mettre en évidence, j’ai porté sur le dessin les signes + et -.

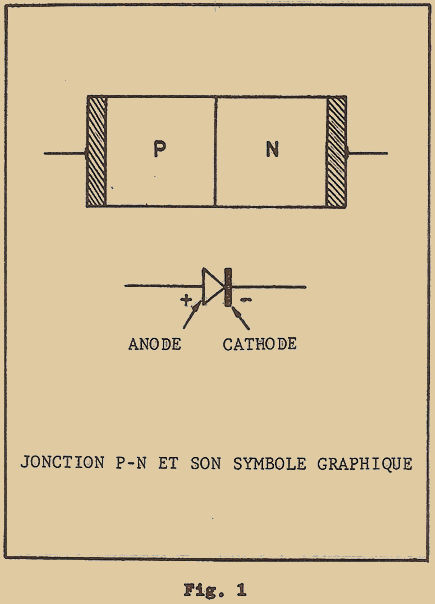
Le côté de la flèche correspond au semi-conducteur P et prend le nom d’Anode. Du côté du plan (trait vertical) c’est au contraire le semi-conducteur N et on l’appelle la Cathode.

Les propriétés d’une diode sont exprimées de façon complète en donnant la caractéristique tension-courant, appelée plus brièvement "caractéristique V - I" où V est le symbole de la tension et I celui du courant. Elle est obtenue, en mesurant différentes valeurs de tension appliquée à la diode et les différents courants qui en résultent.

A la figure 2-a, je vous ai représenté le schéma du circuit utilisé pour appliquer à la diode une tension positive V_d (tension directe).

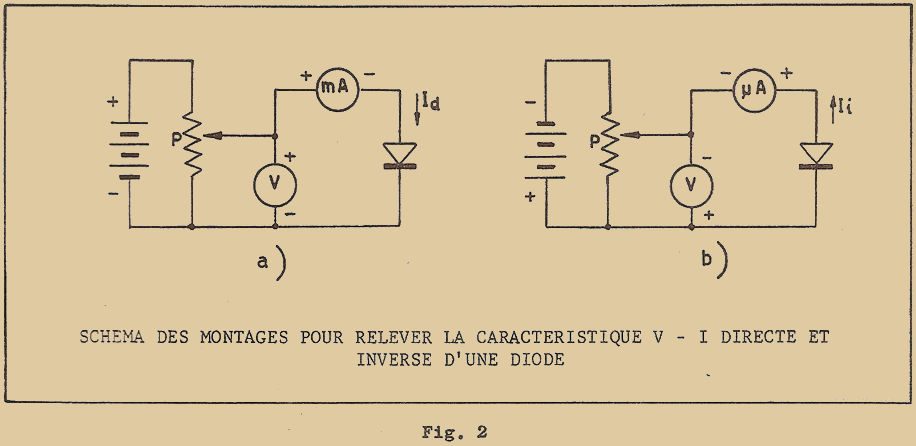
A l’aide d’un potentiomètre P on peut régler la valeur d’une telle tension (qui est mesurée à l’aide d’un voltmètre V) et est par exemple de 1 V, puis 2 V, puis 3 V etc … et on note en même temps, les valeurs correspondantes du courant direct I_d lues sur le milliampèremètre (mA sur le schéma).

D’une façon analogue, on peut appliquer à la diode une tension négative V_i (tension inverse) et pour les différentes valeurs de celle-ci, on note les valeurs correspondantes du courant inverse I_i (figure 2-b) lues sur le microampèremètre (µA sur le schéma).

Tous les couples de valeurs mesurées (chacune constituée par la valeur de la tension et la valeur correspondante du courant) peuvent être reportés sur un graphique, de façon à obtenir ainsi la caractéristique de la diode. Dans ce but, on trace 2 axes de coordonnées (figure 3) et à partir de leur point d’intersection 0 (origine), on gradue l’axe horizontal en volts, - positifs vers la droite, négatifs vers la gauche -, et l’axe vertical en milliampères, - positifs vers le haut (courant direct) et négatifs vers le bas (courant inverse) -. En supposant que la tension directe V_d = 1,5 V et que le courant direct I_d = 5mA, on cherche la valeur 1,5V et sur le demi-axe horizontal de droite et on élève à partir de ce point, une droite verticale (en pointillés sur la figure 3) jusqu’à la hauteur correspondant à 5mA lue sur l’axe vertical vers le haut : on détermine ainsi le point A.

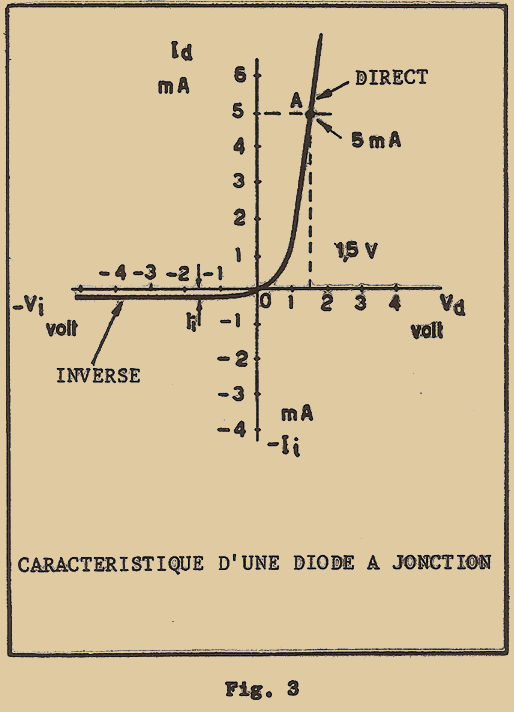
En procédant de la même manière pour toutes les valeurs, en se rappelant qu’il faut porter les valeurs de la tension et du courant direct vers la droite et vers le haut, et les valeurs de la tension et du courant inverse vers la gauche et vers le bas, on détermine autant de points qu’il y a de couples de valeurs ; il suffit alors de relier tous ces points par une ligne pour obtenir la courbe caractéristique de la diode.

Son allure caractéristique est celle de la figure 3. En l’examinant graphiquement, nous pouvons faire les remarques importantes suivantes.

Tout d’abord, la courbe passe toujours par l’origine des axes : en effet, si la tension appliquée est nulle, le courant dans le circuit sera nul aussi. D’autre part, on peut considérer que la courbe globale est formée par l’ensemble de 2 courbes partielles : celle qui se trouve à droite de l’axe vertical, représente le comportement de la diode en polarisation directe ; celle qui se trouve à gauche de l’axe vertical, représente le comportement de la diode en polarisation inverse.

La courbe de droite montre comment en augmentant la tension directe V_d appliquée à la diode, le courant direct I_d augmente très rapidement dès le début. Pour des tensions de quelques volts, le courant atteint déjà les valeurs maxima tolérées par le type de diode considéré (de quelques milliampères, comme sur la figure 3 pour les diodes de faible puissance, à quelques ampères pour les diodes à grande puissance). Arrivés à ce point, nous pouvons faire une observation. Comme nous l’avons vu dans la dernière leçon, la tension directe a pour effet de diminuer la hauteur de la barrière de potentiel de la jonction, jusqu’à atteindre un maximum et l’annuler. Or, si la hauteur de la barrière de potentiel est, à la température ambiante, de quelque 0,3V pour une jonction au germanium, et de 0,7V environ pour une jonction au silicium, on tendrait à croire que la tension maximum que l’on peut appliquer à la diode ne doit pas être supérieure à ces valeurs, alors que la caractéristique de la figure 3 atteint quelques volts. Ceci parait donc en contradiction avec la théorie, car avec une telle polarisation, on devrait non seulement annuler la barrière, mais encore en inverser le sens.

Le fait est que les régions P et N du semi-conducteur que l’on utilise, ne sont pas des conducteurs parfaits, mais présentent une résistance ohmique plus ou moins grande. A cause même de cette résistance, quand la diode est parcourue par un courant, il se produit une chute de potentiel et il n’y a qu’une faible partie de la tension qui se trouve réellement utilisée pour réduire l’amplitude de la barrière de potentiel.

Comme la chute de potentiel dûe à la résistance du semi-conducteur augmente lorsque le courant qui traverse la diode croît, et ceci d’autant plus rapidement que la tension appliquée augmente, il en résulte que l’on peut appliquer des tensions très grandes (qui sont de quelques volts, par rapport aux dixièmes de volt correspondant à la hauteur de la barrière de potentiel) et qu’elles n’arrivent pas à abaisser complètement la barrière de la jonction.

On peut donc en conclure que pour de faibles tensions directes appliquées à la diode, l’amplitude de la barrière est peu affectée et c’est elle qui règle essentiellement le courant. Pour des tensions plus grandes, au contraire la barrière de potentiel est pratiquement réduite à zéro et le surplus de tension appliqué sert à vaincre la résistance du semi-conducteur et ainsi c’est la valeur de cette résistance qui limite le courant.

Si l’on regarde maintenant la caractéristique de gauche qui correspond à la polarisation inverse de la diode, on peut voir qu’en augmentant la tension négative appliquée, le courant devient rapidement égal à une valeur très faible et se maintient à cette valeur lorsque l’on fait croître la tension : la courbe reste par conséquent toujours à la même distance de l’axe horizontal.

Si l’on se rappelle que la tension inverse appliquée à la diode a la même polarité que la barrière de potentiel, on comprend très bien l’allure de cette caractéristique. Le début de la courbe, voisine de l’origine correspond en effet à des tensions inverses très faibles, qui produisent évidemment une augmentation de la hauteur de la barrière de potentiel, mais qui sont insuffisantes pour annuler complètement les flux des porteurs majoritaires. En effet, le courant effectif qui traverse la jonction n’est seulement qu’une faible partie de celui qui correspond aux porteurs minoritaires.

Dès que la tension appliquée a une valeur suffisante pour annuler complètement le flux des porteurs majoritaires, le courant inverse qui traverse la jonction correspond aux seuls flux des porteurs minoritaires. A ce moment, le courant inverse ne peut plus augmenter, puisque le nombre de porteurs minoritaires n’augmente pas avec la tension. La caractéristique qui va en résulter à partir d’un certain point, sera parfaitement horizontale. La caractéristique ne pourra pas être continuée comme on le veut, mais devra être limitée à un certain point pour ne pas dépasser les valeurs maxima de courant et de tension admissibles par la diode. En effet, quand la diode conduit, elle peut être traversée par un courant maximum (sens direct) qui dépend des dimensions physiques de la jonction : plus la section transversale de celle-ci est grande, plus grand pourra être le courant admissible. La caractéristique directe est donc limitée par la valeur maximum I_max du courant admissible par la diode.

En ce qui concerne la caractéristique inverse, la limite sera imposée, non pas par la valeur du courant, qui reste toujours très faible, mais par la tension appliquée : si l’on dépasse une certaine valeur, qui peut aller de quelques dizaines de volts à quelques centaines de volts selon le type de diode, la diode peut être détruite et même déjà avant elle peut ne plus fonctionner de façon correcte. La valeur maximum de la tension inverse que la diode peut supporter est indiquée par V_i max.

Les valeurs maxima du courant direct et de la tension inverse sont des données très importantes, qui ne doivent jamais être dépassées dans les conditions normales de fonctionnement.

Une autre donnée typique de la diode est celle qui est indiquée par I_s (c’est-à-dire courant de "saturation"), La valeur du courant inverse. Il serait bien souhaitable que le courant inverse soit nul (diode idéale) mais ceci n’est pas possible avec une diode réelle. Une diode est donc d’autant meilleure que son courant inverse est plus faible.

La valeur de I_s doit toujours être comparée à la valeur I_max, en ce sens qu’une diode de puissance, capable de délivrer quelques ampères, ne pourra pas avoir un courant inverse aussi faible que celui d’une diode normale dont le courant direct n’est que de quelques dizaines de milliampères.

Il ne suffit pas d’indiquer la valeur de I_s, mais il faut préciser encore à quelle température de la jonction celle-ci a été mesurée : puisque le courant inverse croît rapidement avec la température, à cause de l’accroissement rapide avec celle-ci de la concentration des porteurs minoritaires.

1 – 1 EFFET ZENER

En regardant la caractéristique inverse de la figure 3, on pourrait penser d’après ce que l’on a dit, que la tension inverse peut être augmentée autant que l’on désire, sans que le courant qui a atteint la valeur de saturation correspondant à la concentration des porteurs minoritaires, n’augmente ; ce n’est pas exact : en effet, si l’on continue à augmenter la tension inverse appliquée à la jonction, le courant reste pratiquement constant jusqu’à une valeur bien définie de la tension. Au-delà de cette valeur, il va commencer à croître tellement vite que la caractéristique inverse passe de la position horizontale à la position verticale comme indiqué à la figure 4.

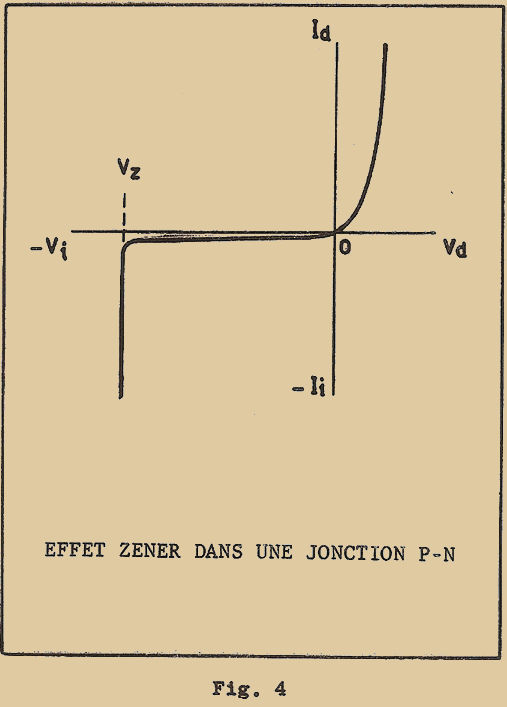
Ceci signifie ; que la jonction présente une résistance très élevée (c’est-à-dire qu’elle conduit peu) tant que la tension inverse qu’on lui applique est inférieure à la valeur V_Z et quelle présente une résistance très faible (c’est-à-dire une conduction très grande) dès que la tension a atteint la valeur V_Z. Il suffit d’augmenter de quelques dixièmes de volt la tension inverse au-delà de la valeur V_Z, pour avoir immédiatement un courant inverse, beaucoup plus grand que si l’on avait polarisé la diode dans le sens direct.

On a donné à ce phénomène le nom d’effet Zener, du nom du savant qui le découvrit pour la première fois et qui en donna une justification, se référant à la théorie générale des semi-conducteurs.

Pour expliquer l’effet Zener, il faut se rappeler que le courant inverse est dû exclusivement aux porteurs minoritaires et considérer l’origine de ces porteurs.

Nous avons vu dans les dernières leçons, que les porteurs minoritaires étaient dus à la formation de paires électron-trou, provoquées par la rupture des liaisons existant entre les atomes du semi-conducteur : nous pouvons dire que normalement nous avons un certain nombre de liaisons "rompues" (et ainsi autant de paires électron-trou) et que la rupture est provoquée par les vibrations des atomes du semi-conducteur qui sont dues à la température.

Mais la vibration des atomes n’est pas la cause unique de la rupture des liaisons ou en d’autres termes, elle n’est pas la seule cause qui agit sur un électron de façon à lui faire quitter son orbite et à obtenir ainsi un électron libre et un trou. De façon plus générale, nous pourrons dire qu’une force quelconque qui agit sur un électron, pourra lui faire quitter son orbite, pourvu qu’elle ait une intensité suffisante.

Il faut se rappeler encore que l’électron est une charge électrique (négative) et que la présence d’un champ électrique fait apparaître une force, d’autant plus grande qu’est plus intense le champ. Cette force va tendre à déplacer l’électron des potentiels négatifs vers les potentiels positifs.

Ainsi, si l’on soumet les atomes d’un semi-conducteur à un champ électrique intense, des forces extrêmement élevées vont agir sur leurs électrons, et quelques-uns d’entr’eux pourront même quitter leur orbite.

Si nous reprenons l’examen d’une jonction, nous verrons qu’il est relativement facile de réaliser les conditions énoncées. En effet, si nous polarisons une jonction en sen inverse, toute la tension inverse va être appliquée à la faible largeur de la barrière de potentiel. Dans la zone de la barrière, apparaît donc un champ électrique E qui peut prendre des valeurs élevées, en fonction de la tension V_G (figure 5). Le champ électrique E est donné par le rapport de l’amplitude de la barrière de potentiel exprimée en volts à la largeur de celle-ci, exprimée en mm.

E = V_G/d avec E en V/mm, V_G en V, d en mm

Pour avoir une idée sur l’intensité du champ électrique, supposons que nous appliquions à la jonction, une tension inverse de 4,5 V ; nous obtenons ainsi une barrière de potentiel dont la hauteur est égale à V_G = V + V_Go ; si le semi-conducteur est du silicium, nous aurons V_Go = 0,7V (voir leçon précédente) et V_G = 4,5 + 0,7 = 5,2V. Supposons par exemple que l’épaisseur de la barrière soit de 3µm (c’est l’ordre de grandeur d’une barrière) soit 0,003mm ; appliquons la formule précédente :

E = 5,2/0,003 = 1.730V/mm

c’est-à-dire que c’est à peu près le dixième du champ électrique crée entre les électrodes des bougies de voiture.

Un tel champ électrique est suffisant pour arracher les électrons des orbites externes des atomes de silicium. Qui se trouvent dans la zone de la barrière, et il se produit ainsi un très grand nombre de paires électrons-trous. On comprend donc pourquoi, dans une telle région la concentration des porteurs minoritaires devient très grande et comment le courant inverse peut prendre des valeurs élevées.

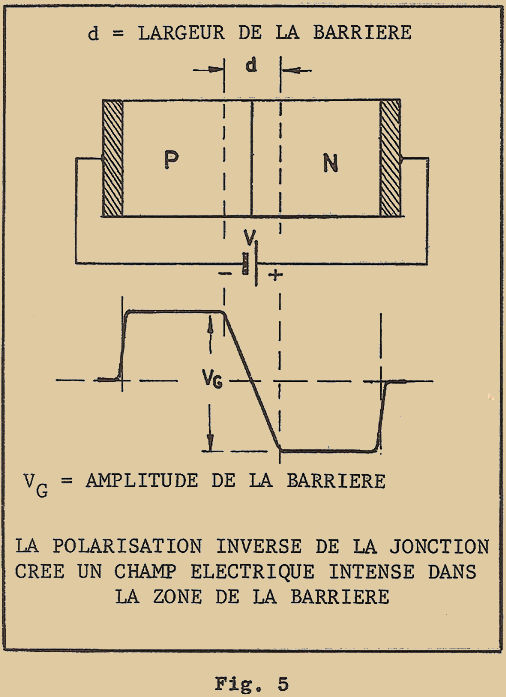
La tension pour laquelle ce phénomène se manifeste est dite tension de Zener et elle est normalement de quelques volts. Elle dépend aussi, bien que de façon moins évidente, de la température mais les variations dUes à ce paramètre sont en général de l’ordre du dixième de volt.

L’effet Zener est d’une très grande importance et est utilisé dans les diodes spéciales, dites diodes de Zener qui fonctionnent comme stabilisatrices de tension, ainsi que nous le verrons plus tard.

Étant donné que de telles diodes stabilisent la tension à la valeur V_Z, il s’avère important de chercher à réaliser des diodes ayant des valeurs de tension Zener différentes, ce que l’on peut obtenir en particulier avec des diodes au silicium soigneusement dopées.

On peut démontrer que la largeur de la barrière dépend de la concentration des atomes donneurs et accepteurs et il est facile de voir, que si cette largeur augmente, on pourra appliquer une tension inverse, proportionnellement plus grande avant que le champ électrique n’atteigne la valeur critique qui provoque l’effet Zener. On peut réaliser ainsi des diodes dont la tension Zener est supérieure à la centaine de volts.

Il faut remarquer aussi, que lorsque la tension Zener est supérieure à environ 10V, le phénomène n’est plus dû à l’effet Zener mais à l’effet d’Avalanche.

En effet, si la largeur de la barrière est assez grande (par rapport aux quelques microns vus ci-dessus), avant que la tension inverse appliquée n’atteigne la valeur suffisante pour créer le champ nécessaire à l’effet Zener, les électrons qui constituent le courant inverse prennent une vitesse très grande.

Si leur vitesse est suffisamment élevée, ils deviennent en mesure de heurter violemment les atomes du semi-conducteur qui se trouvent dans la zone de la barrière et d’en faire sortir quelques électrons périphériques ; ces électrons à leur tour prennent de la vitesse et ayant acquis une vitesse suffisante, libèrent d’autres électrons. Le phénomène se développe très rapidement et c’est pour cette raison qu’on lui donne le nom d’"effet d’Avalanche", car il est semblable à une avalanche, qui partant du sommet d’une montagne, dévale rapidement en grossissant vers la vallée.

Le même raisonnement peut être repris pour les trous, puisqu’ils collaborent aussi à la création de nouvelles paires électron-trou et à la rapide augmentation des porteurs minoritaires.

En pratique, les choses ne sont pas aussi simples et on ne peut pas dire que la rapide augmentation du courant inverse soit dûe exclusivement à l’effet Zener ou à l’effet d’avalanche, mais les 2 effets existent ensemble. Il n’est donc pas tout à fait exact de donner le nom de Zener à toutes les diodes utilisées comme stabilisatrice de tension.

1 – 2 CAPACITÉ D’UNE JONCTION

Une jonction P-N, présente, outre une valeur de résistance qui dépend de la tension qu’on lui applique (valeur faible pour une polarisation directe, valeur très élevée avec une polarisation inverse avec valeur extrêmement faible au moment de l’effet Zener), une valeur de capacité que l’on peut mesurer très facilement à l’aide d’un pont par exemple.

Pour voir de quelle façon une jonction peut se comporter comme un condensateur, nous pouvons faire le raisonnement suivant :

Considérons une jonction P-N non polarisée. Elle peut être subdivisée en trois parties (figure 6) et en particulier : une région A (constituée par le semi-conducteur P), une région B (constituée par la barrière) et une région C (constituée par le semi-conducteur N). Nous pouvons donc remarquer que, tandis que dans les régions A et C il y a des charges mobiles (constituées essentiellement par des porteurs majoritaires), dans la région B il n’y a que des charges fixes puisque les charges mobiles se sont mutuellement compensées, en se recombinant.

Un matériau contenant des charges mobiles peut être considéré comme un conducteur, tandis qu’un matériau ne contenant que des charges fixes se comporte comme un isolant. Ainsi la jonction peut être assimilée à 2 conducteurs métalliques (régions A et C) séparées par un isolant, c’est-à-dire un diélectrique (région B). Mais deux conducteurs métalliques séparés par un isolant constituent un condensateur : la jonction se comporte donc comme un condensateur.

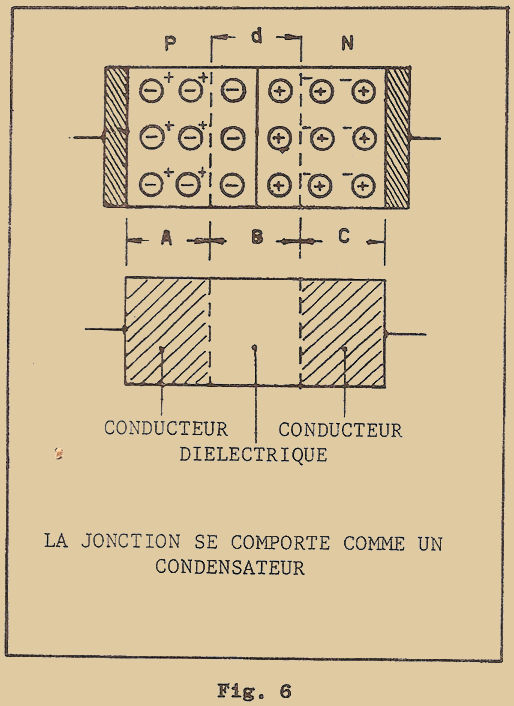
Pour déterminer la capacité de cet étrange condensateur, on peut faire appel à la formule classique pour les condensateurs :

C = Ɛo x Ɛr x S/d C en pF, S en m², d en m

où Ɛo est la constante diélectrique du vide (égale à 8,86 pF/m), Ɛr est la constante diélectrique relative au diélectrique considéré (interposé entre les armatures), S est la surface des armatures et d la distance entre ces dernières.

Dans le cas de la jonction, Ɛr = 16 pour le germanium et 12 pour le silicium ; pour S (surface transversale de la jonction) on peut considérer une valeur moyenne de 1 mm² (soit 0,000.001 m²) ; d = 3µm comme nous l’avons vu précédemment (soit 0,000.003 m). En remplaçant ces valeurs dans la formule, on obtient :

C = 8,86 x 16 x 0,000.001/0,000.003 = 47 pF environ

C’est la valeur de la capacité qui existe dans une jonction non polarisée. Si nous appliquons maintenant à la jonction, une polarisation inverse, l’armature A devient négative et la B positive : les charges libres se trouvent ainsi éloignées de la jonction. Nous avons donc une augmentation de la largeur de la barrière et une diminution de la capacité (figure 7-a). Si nous augmentons la tension inverse de polarisation, la largeur de la barrière augmente encore et la capacité diminue encore (figure 7-b).

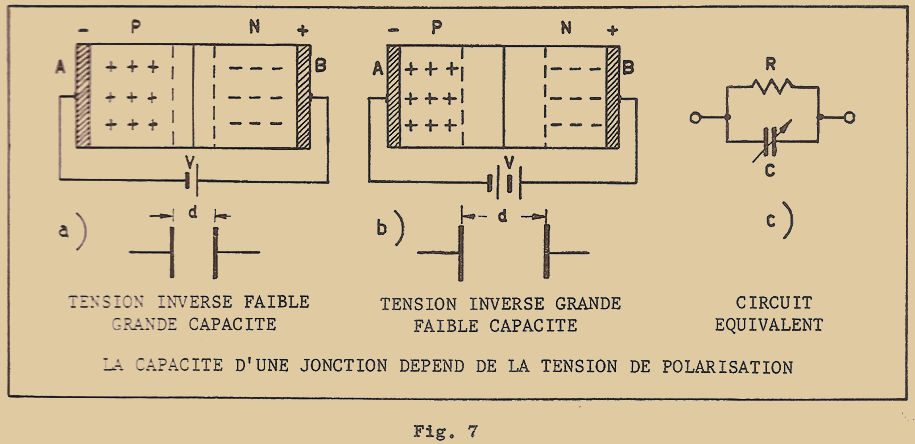
Nous voyons donc que non seulement la jonction présente une certaine capacité, mais que sa valeur peut être variable entre certaines limites, en agissant sur la polarisation inverse. La jonction peut donc être représentée par un schéma équivalent, formé par une capacité variable avec en parallèle une résistance de très forte valeur (figure 7-c).

La résistance indique que le diélectrique n’est pas un isolant parfait puisque qu’il laisse passer un léger courant. En effet, la jonction est traversée par le courant inverse de saturation I_s et se comporte comme une résistance dont la valeur est :

R = V/I_s , où V est la tension de polarisation

Cette propriété de la jonction permet de réaliser des diodes dont le rôle est de fonctionner comme des condensateurs variables et dont la valeur dépend de la tension de polarisation inverse. Ces diodes trouvent des applications, principalement dans les circuits de contrôle automatique de la fréquence des oscillateurs (par exemple dans les oscillateurs locaux des récepteurs FM ou TV).

Des diodes au silicium, spécialement construites, présentent des capacités variables de quelques pF à une centaine de pF, avec des tensions de polarisation variables de quelques volts à quelques dizaines de volts. Ainsi, des diodes redresseuses classiques au silicium, peuvent être utilisées comme des capacités variables. Dans tous les cas, la résistance en parallèle sera comprise entre une centaine de kΩ et 1 MΩ, ce qui ne perturbe pas les circuits oscillants ordinaires.

La capacité que présente une jonction quand elle est polarisée dans le sens direct est beaucoup plus grande qu’elle n’est lors d’une polarisation inverse et peut atteindre ainsi des valeurs d’une dizaine de mille de pF. Le phénomène est alors beaucoup plus complexe que celui que je vous ai décrit tout à l’heure, car la diode conduit et l’on ne peut plus considérer que la zone de la barrière est sans charges libres.

D’un autre côté, la valeur de R est très faible (la diode conduit) : la capacité est ainsi pratiquement court-circuitée et son effet est presque toujours négligeable.

Si la capacité de la jonction polarisée en inverse peut être exploitée en utilisant la diode comme un condensateur variable, elle est par contre très gênante, lorsque l’on utilise la diode comme un simple redresseur ou détecteur et elle devient pratiquement inutilisable dès que la fréquence est un peu supérieure à la gamme acoustique.

Ceci est dû au fait que la capacité aux fréquences élevées présente une réactance faible : elle court-circuite pratiquement la résistance inverse élevée de la diode, et ainsi celle-ci conduit en même temps dans les deux sens et par la même, perd sa propriété de redressement.

Les diodes à jonction, utilisées comme redresseurs, ne peuvent travailler qu’à des fréquences basses, pour convertir par exemple le courant alternatif en courant continu, mais ne peuvent être utilisées comme détecteurs des fréquences HF modulées.

2 – PROPRIÉTÉS DES JONCTIONS P-N

Si nous résumons maintenant tout ce qui a été étudié dans cette leçon à propos des jonctions, nous pourrons dire qu’une jonction P-N présente trois propriétés principales, qui permettent d’utiliser une diode pour trois rôles différents :

1. comme REDRESSEUR, en la faisant travailler dans les parties de la caractéristique directe et de la caractéristique inverse, sans atteindre la tension de Zener.
2. comme STABILISATEUR DE TENSION en la faisant travailler dans la partie verticale de la caractéristique inverse, c’est-à-dire à la tension Zener
3. comme CONDENSATEUR VARIABLE en la faisant travailler dans la partie horizontale de la caractéristique inverse, c’est-à-dire entre de faibles valeurs de la tension de polarisation et la tension Zener.

3 – DIODE A POINTES

Un autre type de diode, dérivé de la diode à jonction, est appelé diode à pointes ou diode cristal. On utilise encore la propriété de redressement que présente un contact à pointes, c’est-à-dire dont les dimensions sont extrêmement faibles, obtenu en appuyant un fil métallique très mince sur un morceau de semi-conducteur.

Cette propriété était déjà connue à la fin du siècle dernier, lorsqu’on utilisait pour la détection des ondes électromagnétiques le cristal de galène constitué par un morceau de sulfure de plomb (galène) sur lequel on appuyait une "moustache de chat".

La diode à pointe n’est qu’une version moderne et améliorée de l’antique diode à galène, dans laquelle la galène est remplacée par du germanium ou du silicium N, sur lequel on appuie la pointe d’un mince fil (en général en bronze phosphoreux), formé en ressort, de façon à garantir une pression légère et constante sur le semi-conducteur et d’éviter ainsi que le contact ne puisse devenir incertain. Je vous ai représenté à la figure 8-a, la constitution d’une diode à pointe et à la figure 8-b, je vous ai reporté son symbole graphique, identique à celui d’une diode à jonction.

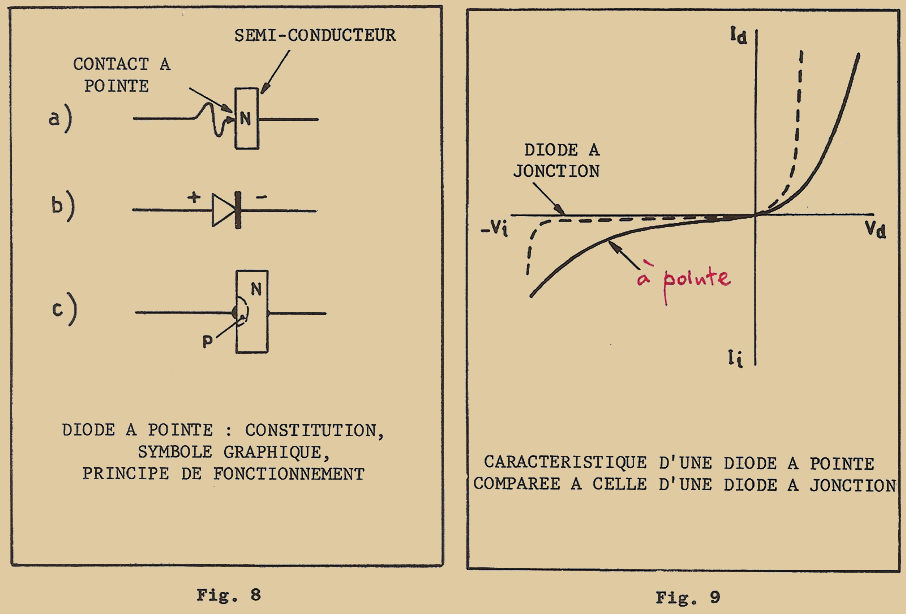
Bien que la propriété de redressement du contact à pointes ait été exploitée depuis fort longtemps, le fonctionnement d’une telle diode n’est pas encore parfaitement clair et s’explique à l’aide de différentes théories, parmi lesquelles la plus simple et la plus probable est celle qui est tirée de la théorie de fonctionnement des diodes à jonction.

Il faut encore remarquer, que la qualité de redressement du contact à pointes est fortement augmentée, si l’on soumet la diode au processus de "formation" qui consiste à faire traverser le contact même, par de fortes impulsions de courant, de très brève durée. Un tel procédé, (développé pendant la dernière guerre mondiale, lorsque les diodes ont commencé à être utilisées dans les installations Radar) a la propriété de diminuer fortement la résistance directe et d’augmenter beaucoup sa résistance inverse quand elle est polarisée en sens inverse, ce qui signifie que le courant inverse est fortement réduit.

Pendant le processus de "formation", les fortes impulsions de courant (dont l’intensité atteint quelques centaines demA, c’est-à-dire des valeurs qui sont presque des dizaines de fois plus grandes que le courant maximum admissible pour un fonctionnement normal de la diode) font fondre partiellement la très fine pointe métallique, et facilitent ainsi la diffusion des atomes du métal dans le semi-conducteur. On obtient ainsi un véritable dopage du semi-conducteur, avec comme effet, de transformer le type N en type P dans le voisinage immédiat du contact à pointes, et de créer une minuscule jonction P-N à laquelle est dûe la propriété de redressement de la diode (figure 8-c).

La caractéristique de la diode à pointes est très semblable à celle d’une diode à jonction, comme vous pouvez le voir sur la figure 9 où la première a été tracée par une ligne continue et la seconde par une ligne en pointillés ; si vous regardez une telle figure, vous pouvez remarquer tout de suite deux différences. Dans la partie de droite (polarisation directe), la courbe continue est beaucoup plus "basse" que celle qui est en pointillés : ceci signifie qu’à une même tension appliquée, le courant qui traverse une diode à pointes est plus faible que celui qui traverse une diode à jonction. En d’autres termes, la diode à pointes présente une résistance directe, plus grande que celle d’une diode à jonction.

Dans la partie de gauche (polarisation inverse), le courant inverse ne reste pas constant lorsque l’on augmente la tension de polarisation, c’est-à-dire qu’il n’atteint pas une valeur de saturation comme pour une diode à jonction (ligne en pointillés) mais augmente continuellement avec la tension (ligne continue). L’explication d’un tel phénomène peut être donnée par le fait que la jonction qui s’est formée autour du contact est tellement petite, qu’elle s’échauffe rapidement au passage du courant inverse. Il est facile alors de comprendre, qu’un tel échauffement provoque une augmentation de la concentration des porteurs minoritaires et qu’ainsi il y a augmentation du courant inverse.

Une plus grande résistance directe, et une valeur plus grande du courant inverse font que la diode à pointes a des qualités inférieures à celles d’une diode à jonction. Par contre, elle a un avantage énorme : la très faible capacité de la jonction, dûe à ses dimensions réduites, permet son utilisation à des fréquences très élevées. Les diodes à pointes sont principalement utilisées comme détecteurs des ondes HF modulées en amplitude ou en fréquence, domaine d’application où les diodes à jonction ne peuvent être utilisées pour les raisons que nous avons vues.

Il faut remarquer, qu’en raison de l’augmentation continuelle du courant inverse avec l’augmentation de la tension appliquée, on ne constate pas d’effet Zener dans les diodes à pointes.

Enfin, les propriétés de redressement d’un contact à pointes fait sur des semi-conducteurs P sont nettement inférieures à celles d’un contact sur des semi-conducteurs du type N. C’est pour cette raison que toutes les diodes à pointes sont obtenues à partir des semi-conducteurs du type N.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 5^ème LEÇON THÉORIQUE

1 – La jonction P-N est formée par la réunion de deux blocs de semi-conducteurs de type différent : c’est-à-dire du type P et du type N.

2 – La barrière de potentiel est dûe aux charges fixes existant dans les deux semi-conducteurs, dans le voisinage immédiat de la jonction et qui ne sont plus compensées par les charges mobiles correspondantes car celle-ci ont diffusé à travers la jonction elle-même.

3 – Si l’on néglige la présence des porteurs minoritaires (explication simplifiée), on peut dire que la hauteur de la barrière de potentiel croît jusqu’à l’annulation de la diffusion des charges mobiles à travers la jonction.

4 – La valeur atteinte par la barrière de potentiel est de 0,3V pour une jonction au germanium et 0,7V pour une jonction au silicium. Les valeurs ne sont pas mesurables : elles ont été déterminées par voie de calcul et correspondent à une température de 300°K.

5 – La polarité de la barrière de potentiel est telle qu’elle s’oppose à la traversée de la jonction des porteurs majoritaires et qu’elle favorise par contre celle des porteurs minoritaires.

6 – Si l’on réunit les extrémités d’une jonction non polarisée on ne constate aucun courant au travers de celle-ci car il n’y a, à l’intérieur, aucun phénomène capable de développer de l’énergie.

7 – Une jonction P-N se comporte comme une diode, car elle ne conduit le courant que dans un sens, c’est-à-dire seulement lorsque le semi-conducteur P est rendu positif par rapport au semi-conducteur N.

8 – Le courant inverse d’une jonction croît avec la température car avec celle-ci la concentration des porteurs minoritaires augmente.

9 – Le courant direct d’une jonction est constitué par les flux des porteurs majoritaires.

---

EXERCICES DE RÉVISION SUR LA 6^ème LEÇON THÉORIQUE

1 – Qu’exprime la caractéristique V – I d’une diode  ?

2 – A quelles valeurs correspond le courant inverse d’une diode  ?

3 – Qu’appelle-t-on tension de Zener  ?

4 – Quelle différence y a-t’ il entre l’effet Zener et l’effet d’avalanche  ?

5 – Qu’est-ce qu’une diode Zener  ?

6 – Dans quelles conditions, une diode à jonction peut-elle se comporter comme un condensateur variable et pourquoi  ?

7 – Quels sont les avantages et les inconvénients à utiliser une diode à jonction comme condensateur variable  ?

8 – Quelles sont les limites du courant direct et de la tension inverse pour une diode fonctionnant en redresseuse  ?

9 – En regardant la caractéristique d’une diode comment peut-on établir s’il s’agit d’une diode à jonction ou d’une diode à pointes  ?

Fin de la leçon 6

---

LECON 7

1 – LE TRANSISTOR JONCTION

Dans la leçon précédente, nous avons étudié les propriétés de la jonction P-N et nous avons vu ses applications pratiques, en particulier comme diode à jonction.

Nous allons étudier maintenant, le comportement d’un dispositif plus complexe, formé de trois semi-conducteurs disposés les uns à la suite des autres et dont deux consécutifs sont de types différents. Nous voyons tout de suite que de cette façon, nous pouvons obtenir deux dispositions différentes : nous pouvons en effet, placer un semi-conducteur P entre deux semi-conducteurs N comme indiqué sur la figure 1-a, ou bien au contraire placer un semi-conducteur N entre deux semi-conducteurs P (figure 1-b).

Le montage sera encore complété par 3 armatures métalliques placées respectivement aux extrémités des semi-conducteurs latéraux et sur le côté du semi-conducteur central et repérées par les lettres E – B et C. On donne à ce montage le nom de TRANSISTOR.

Pour bien distinguer les deux types, le dispositif de la figure 1-a sera appelé Transistor NPN, et celui de la figure 1-b, Transistor PNP.

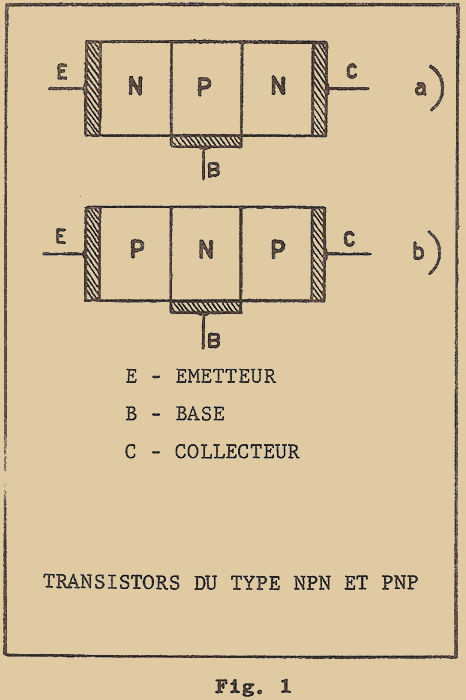
Nous appellerons encore le semi-conducteur central BASE (d’où la lettre B donnée à l’armature et à la connexion correspondante) et les semi-conducteurs externes seront nommés EMETTEUR et COLLECTEUR (d’où les lettres E et C portées à côté des connexions).

Les caractéristiques des deux types de transistors sont parfaitement identiques, et pour cette raison, il suffit de n’en étudier qu’un seul. Tout ce qui va être dit va être dit dans ce qui va suivre pour un type, pourra être repris pour l’autre type en remplaçant les trous par les électrons, les électrons par les trous et en intervertissant les polarités des tensions appliquées aux électrodes (émetteur, base, collecteur).

En d’autres termes, nous pouvons dire que les deux types de transistors fonctionnent de la même manière, mais nécessitent des tensions de polarité opposée : ainsi, le transistor NPN fonctionne avec des tensions positives, tandis que le transistor PNP fonctionne avec des tensions négatives.

Si nous observons la figure 1, nous remarquons que les trois semi-conducteurs forment deux jonctions distinctes. Dans le cas du transistor NPN, l’émetteur et la base forment une jonction N-P tandis que la base et le collecteur forment une jonction P-N.

Dans le cas du transistor PNP au contraire, l’émetteur et la base forment une jonction P-N, tandis que la base et le collecteur forment une jonction N-P.

Si de telles jonctions doivent être polarisées, il est évident que les tensions appliquées aux électrodes du transistor devront être de polarité différente suivant le type du transistor utilisé. Par exemple, si nous voulons que la jonction émetteur-base soit polarisée dans le sens direct, il faudra relier le pôle positif de la pile sur la base et le négatif sur l’émetteur dans le cas du transistor NPN, tandis que dans le cas du transistor PNP il faudra relier le pôle positif à l’émetteur et le négatif sur la base.

Ayant établi ces considérations sur les analogies et les différences des deux types, nous pouvons passer à l’étude des caractéristiques et du fonctionnement des transistors, en ne considérant qu’un seul type, par exemple le NPN.

Quand on n’applique aucune tension extérieure au transistor, celui-ci se comporte de la même manière que deux jonctions de type différent (une jonction N-P et une P-N dans le cas du transistor NPN) réunies ensemble et non polarisées.

Pour chacune des jonctions, nous pouvons reprendre les considérations faites dans les leçons précédentes : nous pourrons en conclure, qu’à cause de la diffusion des porteurs majoritaires, il se forme deux barrières et qu’ainsi il apparait deux barrières de potentiel (chacune correspondant à une jonction) qui sont

opposées

, puisque les deux jonctions sont de type différent.

Ainsi, si nous négligeons pour simplifier les potentiels des armatures métalliques auxquelles sont reliées les connexions, et si nous ne considérons que les potentiels des semi-conducteurs, les barrières de potentiel ont l’allure indiquée sur la figure 2. En effet, les deux régions N se chargent à un potentiel positif, représenté sur la figure par la ligne en traits pleins et dessinée en dessous de la ligne de référence (potentiel zéro), qui elle est tracée en traits pointillés, tandis que la région centrale P se charge à un potentiel négatif représenté par la ligne au-dessus de la référence.

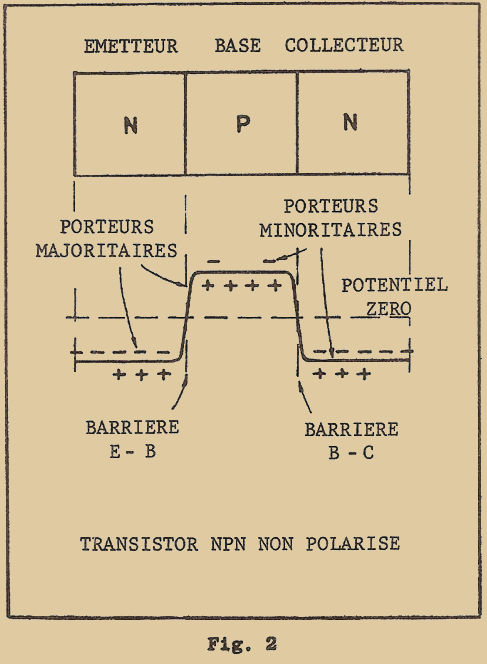
La hauteur des deux barrières dépend, comme nous l’avons vu, de la température à laquelle sont portés les semi-conducteurs et de leur dopage. Si les deux régions extrêmes sont dopées identiquement (c’est-à-dire si la concentration des porteurs est la même dans les deux régions) les deux barrières qui en résulteront auront même amplitude, comme c’est le cas dans la figure 2. Si au contraire, les concentrations sont différentes, la barrière qui correspond à la région la plus dopée sera la plus grande.

Ceci n’apporte aucune différence en ce qui concerne le fonctionnement du transistor. Ainsi, nous verrons par la suite qu’en pratique les deux régions extrêmes n’ont pas la même concentration des porteurs. Pour le moment nous supposerons pour simplifier que les deux barrières de potentiel ont même hauteur.

En l’absence de polarisation extérieure, le transistor ne sera parcouru par aucun courant, car les deux jonctions sont en régime d’équilibre dynamique, comme nous l’avons étudié pour la jonction P-N.

Selon la théorie, de l’équilibre dynamique, nous avons ainsi quatre flux de porteurs à travers chacune des jonctions, comme il est indiqué sur la figure 3.

À travers la jonction émetteur-base, nous avons deux flux de charges négatives (électrons) qui se compensent : un de l’émetteur vers la base dû aux porteurs majoritaires (électrons présents dans l’émetteur du type N) et indiqué par F_nEB ; l’autre de la base vers l’émetteur dû aux porteurs minoritaires (électrons présents dans la base du type P) et indiqué par f_nBE. D’autre part, nous avons deux flux de charges positives (trous) qui ne sont pas nécessairement égaux à ceux des charges négatives que nous venons de voir, mais égaux entr’eux de façon à pouvoir se compenser : un flux de la base vers l’émetteur dû à des porteurs majoritaires et indiqué F_pBE, et un autre de l’émetteur vers la base dû à des porteurs minoritaires et indiqué par f_pEB.

D’autres flux existent au travers de la jonction collecteur-base ; F_nCB flux d’électrons du collecteur vers la base ; f_pBC flux de trous de la base vers le collecteur ; f_nBC flux d’électrons de la base vers le collecteur ; f_pCB flux de trous du collecteur vers la base. Les deux premiers sont dûs aux porteurs majoritaires et sont respectivement équilibrés par les deux autres, dûs aux porteurs minoritaires.

1 – 1 POLARISATION DE LA JONCTION COLLECTEUR-BASE

Pour un fonctionnement correct du transistor, qu’il soit du type PNP ou NPN, la jonction base-collecteur devra toujours être polarisée en sens inverse, c’est-à-dire que la tension appliquée doit avoir une polarité telle qu’elle augmente l’amplitude de la barrière de potentiel de cette jonction.

Dans le cas des transistors du type NPN, on devra donc relier le collecteur au pôle positif et la base au pôle négatif de la pile de polarisation.

Quand seule la jonction collecteur-base est polarisée et qu’aucune tension n’est appliquée à la jonction émetteur-base, il est évident que le transistor se comporte exactement comme une diode (constituée par la base et le collecteur) polarisée en sens

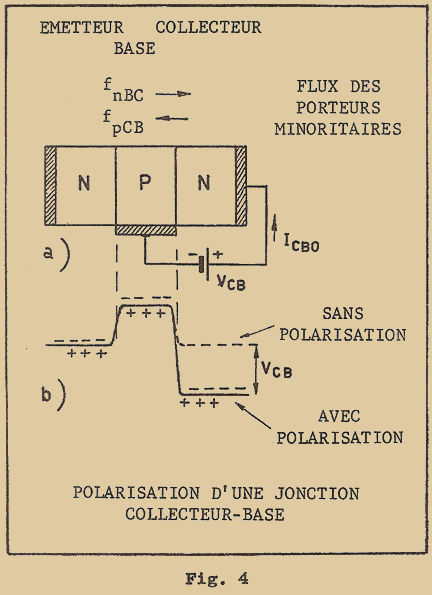
La figure 4 illustre cette condition de fonctionnement : entre les armatures métalliques du collecteur et de la base, on a branché la pile de polarisation, de façon à rendre le collecteur positif par rapport à la base (figure 4-a). La valeur de polarisation V_CB (l’indice CB indique la tension appliquée entre collecteur et base) peut varier de quelques volts à quelques dizaines de volts, selon le type du transistor (faible, moyenne ou grande puissance).

A la figure 4-b, je vous ai reporté au contraire le diagramme qui représente les barrières de potentiel des deux jonctions. Alors que l’amplitude de la barrière correspondant à la jonction émetteur-base, reste la même que précédemment (figure 2), puisqu’elle n’est pas polarisée, l’amplitude de la barrière correspondant à la jonction collecteur-base se trouve accrue de la valeur V_CB.

Si l’on se rappelle ce qui a été dit à propos de la jonction P-N polarisée en sens inverse, il est facile de prévoir l’effet d’une telle polarisation sur les flux des porteurs à travers la jonction. En effet, l’augmentation de l’amplitude de la barrière devient un obstacle infranchissable pour les porteurs majoritaires, tandis qu’elle favorise le passage des porteurs minoritaires. Les flux F_nCB et f_pBC de la figure 3 sont ainsi annulés, tandis que les flux des porteurs minoritaires f_nBC et f_pCB restent inchangés. Ceux-ci constituent le courant inverse de la jonction collecteur-base, que l’on appelle en général courant de saturation du collecteur ou mieux courant résiduel, ce qui est indiqué par le symbole I_CBo (et se lit "i, cé, bé zéro") ; l’indice CBo indique que le courant est celui qui traverse la jonction collecteur-base, lorsque le courant qui traverse la jonction émetteur-base est nul, c’est-à-dire lorsque celle-ci n’est pas polarisée.

La valeur de I_CBo est très faible, puisqu’il s’agit d’un courant inverse, et peut varier entre quelquesµA à quelquesmA selon le type du transistor. Elle ne dépend pratiquement pas de la tension V_CB appliquée au collecteur, mais est très sensible à la température à laquelle se trouve le transistor.

Puisque I_CBo est dû uniquement aux porteurs minoritaires présents dans les deux régions du semi-conducteur qui constituent la base et le collecteur, il faut encore remarquer qu’il est d’autant plus grand que plus grande est la concentration de ces porteurs.

1 -2 POLARISATION DE LA JONCTION ÉMETTEUR-BASE

De ce qui vient d’être dit, nous déduisons que le courant de collecteur peut augmenter à partir de la valeur I_CBo à une valeur I_C quelconque, si d’une façon ou d’une autre, nous pouvions augmenter la concentration des porteurs minoritaires existant dans la base et le collecteur.

Ceci est possible d’une manière très simple : en polarisant dans le sens direct, la jonction émetteur-base. De façon plus précise, on n’obtient seulement qu’une augmentation des porteurs minoritaires présents dans la base (des électrons dans le cas d’un transistor NPN, des trous dans le cas d’un transistor PNP) et non pas des porteurs minoritaires présents dans le collecteur, mais cela suffit pour que le courant du collecteur augmente d’intensité.

Pour comprendre comment la polarisation de la jonction émetteur-base fait croître le courant du collecteur, il suffit de considérer la figure 5. A la figure 5-a, je vous ai représenté le transistor NPN dont les deux jonctions sont polarisées en même temps, à l’aide de deux piles différentes.

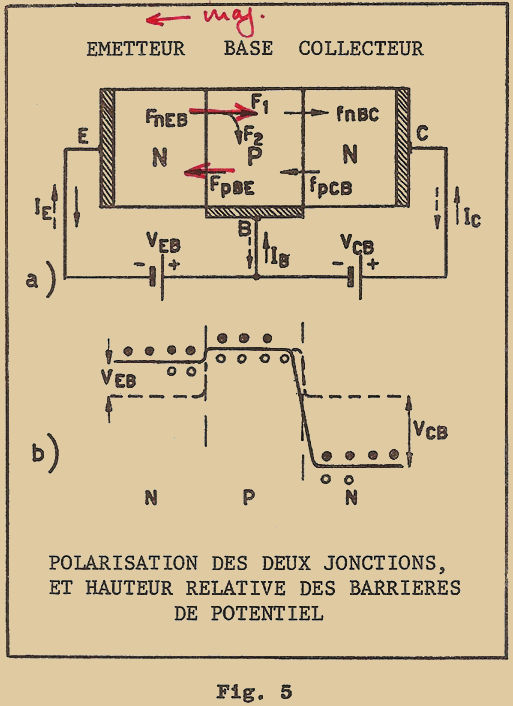
On applique au collecteur, la tension V_CB qui le rend positif par rapport à la base. A l’émetteur au contraire, on applique la tension V_EB qui le rend négatif par rapport à la base. Dans ces conditions, la jonction collecteur-base se trouve polarisée en sens inverse, c’est-à-dire qu’elle n’est traversée que par les flux des porteurs minoritaires f_nBC et f_pCB comme nous l’avons vu précédemment.

La jonction émetteur-base se trouve polarisée au contraire dans le sens direct, et elle est ainsi traversée par deux flux de porteurs majoritaires F_nEB et F_pBE et par deux flux de porteurs minoritaires f_nBE et f_pEB. En se rappelant ce qui a été vu en son temps sur une jonction polarisée en sens direct, on peut dire que les flux dûs aux porteurs minoritaires sont très faibles par rapport à ceux dûs aux porteurs majoritaires, et que pour simplifier, tout en gardant une approximation très bonne, on peut négliger les minoritaires. On dira alors, que la jonction émetteur-base n’est traversée que par les porteurs majoritaires comme indiqué sur la figure 5a.

La tension de polarisation V_EB de la jonction émetteur-base est au maximum de quelques dixièmes de volt, déjà nettement suffisante pour abaisser notablement la barrière de potentiel et donner un flux intense de porteurs majoritaires.

Pour tous les trous qui diffusent de la base vers l’émetteur, tout se passe de la même façon que pour une diode polarisée dans le sens direct.

Ainsi, dès que les trous ont atteint l’émetteur, ils se recombinent avec des électrons qui y sont présents, pendant que d’autres électrons sont fournis par la pile à l’émetteur. Pendant ce même temps, la pile récolte un même nombre d’électrons de la base, et au voisinage de la connexion de base, de nouveaux trous se forment et le phénomène peut ainsi se poursuivre.

C’est d’une manière tout à fait différente que se comporte le flux d’électrons F_nEB. Si l’on regarde la figure 5-b, on voit que les boules noires (qui représentent les électrons) présents dans l’émetteur, une fois qu’elles ont escaladé la barrière et qu’elles ont atteint la base, diffusent dans celle-ci, et se comportent alors comme des porteurs minoritaires, puisque la base est du type P. Comme les porteurs minoritaires des électrons sont sollicités à descendre la barrière de potentiel existant entre la base et le collecteur et à aller vers ce dernier (n’oublions pas que la polarisation inverse d’une jonction base-collecteur favorise le passage des porteurs minoritaires).

Le principe de fonctionnement du transistor est donc le suivant : les électrons "émis" par la région de gauche, à cause de la polarisation directe de la jonction émetteur-base, tendent à atteindre la région de droite (c’est-à-dire qu’ils sont "recueillis") à cause de la polarisation inverse de la jonction base-collecteur ; d’où le nom d’émetteur donné à la région de gauche et de "collecteur" à la région de droite.

Quand la jonction émetteur-base est polarisée dans le sens direct, comme nous l’avons dit, le flux des porteurs minoritaires à travers la jonction base-collecteur est constitué par le flux f_pCB très faible dû aux trous présents dans le collecteur, et par le flux f_nBC notablement plus grand qui est dû au grand nombre d’électrons qui se trouvent dans la base et qui y sont injectés par l’émetteur.

Il faut encore souligner, que tous les électrons "émis" par l’émetteur n’atteignent pas le collecteur : une partie de ceux-ci en effet, pendant leur voyage à travers la base, se recombinent avec des trous qui y sont présents : seuls ceux qui atteignent le sommet de la barrière base-collecteur peuvent "rouler" vers le bas et atteindre le collecteur. Le flux d’électrons F_nEB fournis par l’émetteur à la base, se divise dans la base même en deux parties.

F₁ constitué par les électrons qui vont atteindre la jonction base-collecteur, sans se recombiner à des trous de la base ; ce sont eux qui vont accroître le flux f_nBC et produire une augmentation du courant I_C du collecteur.

F₂ constitué par les électrons qui vont se recombiner avec des trous de la base et ainsi ne pourront atteindre le collecteur ; ce flux ne contribue donc d’aucune façon à l’augmentation du courant I_C puisqu’il fournit le courant qui va se diriger vers la connexion de la base.

Nous avons vu ce qui se passait à l’intérieur du transistor ; voyons maintenant ce qui se passe dans les circuits extérieurs, c’est-à-dire les courants qui parcourent les connexions d’émetteur, de base et du collecteur, et que l’on appelle respectivement I_E - I_B et I_C.

Le courant I_C du collecteur est dû exclusivement aux flux des porteurs minoritaires à travers la jonction base-collecteur, c’est-à-dire aux flux f_pCB et f_nBC. Le premier de ces flux (f_pCB) reste pratiquement de même intensité qu’il y ait ou non une polarisation émetteur-base. Le second (f_nBC) augmente avec la polarisation de la jonction émetteur-base et ceci grâce au flux F₁.

Le courant I_E qui traverse la connexion de l’émetteur est dû par contre aux flux des porteurs majoritaires F_nEB et F_pBE qui traversent la jonction émetteur-base.

Il n’est pas difficile de voir que l’augmentation du courant de collecteur est toujours inférieure à celle du courant de l’émetteur : en effet, cette augmentation est donnée par le flux F₁ qui n’est seulement qu’une partie du flux F_nEB ; mais à son tour, le flux F_nEB ne représente seulement qu’une partie du courant I_E, car I_E est non seulement constitué par le flux F_nEB mais aussi par le flux F_pBE.

Le courant I_B qui traverse la connexion de base est constitué par le flux F_pBE, par le flux F₂ et par le flux f_pCB.

On peut ainsi établir rapidement une relation entre les trois courants du transistor, en observant que le courant I_E se subdivise en deux parties : un courant qui contribue à l’augmentation du courant de collecteur, et un autre courant qui se dirige vers la connexion de la base. Ainsi, on peut dire que dans tous les cas, on a :

I_E = I_C + I_B

ou si l’on préfère :

I_C = I_E - I_B

Comme on le verra par la suite, il est souhaitable que le courant I_C soit le plus possible égal à I_E. Ceci signifie donc, qu’il faut chercher à rendre le courant de base I_B le plus faible possible. Pour atteindre ce but, il faudra rechercher des "astuces" de fabrication pour réduire au maximum les flux f_pCB, F₂ et F_pBE.

Le flux f_pCB est déjà très faible comme je vous l’ai dit, et dans la plupart des cas, il pourra être négligé devant les autres. En effet, ce flux est dû aux porteurs minoritaires (trous) présents dans le collecteur et il contribue à produire le courant I_CBo. En général, on n’a pas besoin de recourir à des tours de force pour le réduire.

Pour réduire le flux F₂ la seule solution est de rendre le plus faible possible le nombre de trous que les électrons peuvent rencontrer dans leur voyage à travers la base. Il est évident que moins il y aura de trous rencontrés, moins les électrons auront de chance de se recombiner, et les possibilités d’atteindre le collecteur seront plus grandes.

Dans la fabrication pratique des transistors, ceci peut être atteint de deux façons différentes, qui sont d’ailleurs en général utilisées ensemble.

La première consiste à rendre la base la plus mince possible ; il est évident que de cette façon, le parcours des électrons est réduit ainsi que leurs probabilités de se recombiner avec des trous de la base.

La seconde consiste à doper très faiblement le semi-conducteur P dont est faite la base : de cette façon, on diminue le nombre de trous existant dans la base.

A l’aide de ces deux "astuces" que je viens de vous décrire, presque tous les électrons "émis" par l’émetteur, traversent la base sans se recombiner et atteignent le collecteur.

Enfin, il faut réduire au minimum le flux F_pBE, ce qui équivaut à faire en sorte que le courant I_E à l’intérieur du transistor soit constitué presque exclusivement par le flux F_nEB c’est-à-dire uniquement par des électrons. Comme le flux F_nEB est dû à des électrons de l’émetteur qui sous l’action de la tension de polarisation traversent la jonction émetteur-base et atteignent la base, tandis que le flux F_pBE est dû à des trous existants dans la base et qui sous la tension de polarisation se dirigent vers l’émetteur, il est facile de voir comment on peut faire pour réduire dans les proportions désirées les intensités de ces flux.

Il suffit de penser que si dans la base il n’existait aucun trou, le flux F_pBE serait nul et il n’y aurait que le flux d’électrons F_nEB. En pratique, on ne peut atteindre cet idéal, mais on peut réduire le flux des trous, et le rendre négligeable par rapport à celui des électrons, en dopant différemment l’émetteur et la base ; il suffira donc de prendre pour l’émetteur du germanium fortement dopé pour avoir une forte concentration d’électrons, tandis que pour la base on utilisera du germanium faiblement dopé pour obtenir une très faible concentration de trous (le faible dopage de la base est d’autre part, très utile pour la réduction du flux F₂ comme nous l’avons vu précédemment).

Avec ces précautions (émetteur fortement dopé, base faiblement dopée et très mince) on arrive à faire en sorte que le courant I_E soit presque uniquement constitué par des électrons émis par l’émetteur, et que presque tous ces électrons peuvent être recueillis par le collecteur. En d’autres termes, on obtient un courant de collecteur dont l’intensité est presque celle du courant d’émetteur.

2 - COEFFICIENT D’AMPLIFICATION DE COURANT "ALPHA"

De l’étude que nous venons de faire sur le comportement du transistor lorsque les deux jonctions sont polarisées, nous pouvons tirer les conclusions suivantes :

Le courant de collecteur, étant constitué par le courant inverse de la jonction base-collecteur, ne dépend pas de la tension (inverse) appliquée à cette jonction, mais dépend de la concentration des porteurs minoritaires présents dans la base. Comme cette concentration peut être augmentée à volonté en agissant sur la polarisation directe de la jonction émetteur-base, il en résulte que le courant de collecteur dépend presque exclusivement de la tension appliquée entre émetteur et base, c’est-à-dire du courant d’émetteur I_E.

Si I_E augmente, I_C augmente aussi ; si I_E diminue, I_C décroît de même : en d’autres termes, le courant de collecteur suit toutes les variations du courant d’émetteur. Seulement, lorsque I_E s’annule, I_C ne s’annule pas complètement, puisque comme nous l’avons vu, le courant de collecteur se réduit à la valeur de saturation I_CBo.

Une telle valeur est de l’ordre de grandeur de quelquesµA seulement, tandis que dans les conditions normales de fonctionnement, le courant d’émetteur est de l’ordre de quelquesmA, c’est-à-dire 1.000 fois plus environ. Le courant de saturation I_CBo peut ainsi être négligé par rapport à la valeur du courant de collecteur (dans les conditions normales de fonctionnement).

Si l’on néglige alors le courant I_CBo, on peut dire que le courant de collecteur I_C est presque égal au courant d’émetteur I_E ou plus exactement que I_C a une valeur légèrement inférieure à celle de I_E. Il est alors intéressant de définir comme coefficient d’amplification de courant, le rapport entre la valeur du courant de collecteur et la valeur du courant d’émetteur. Ce coefficient d’amplification est en général indiqué par la lettre grecque "alpha" dont le symbole est "α" :

α = I_C/I_E

Puisque comme nous l’avons vu, le courant de collecteur est toujours légèrement inférieur à celui d’émetteur, on en déduit que α est toujours inférieur à 1, mais très près de cette valeur. Dans les transistors couramment utilisés dans les récepteurs radio, la valeur de α varie entre une valeur minimum de 0,95 et une valeur maximum de 0,995. Ceci signifie donc que le courant I_C a, selon le type de transistor, une valeur qui varie entre 95 % et 99,5 % de la valeur du courant I_E.

Si par exemple, un transistor donné a un α de 0,98 et si dans son circuit d’émetteur (c’est-à-dire dans son circuit d’entrée) on fait circuler un courant I_E de 5mA, le courant qui circulera dans le circuit du collecteur (c’est-à-dire dans son circuit de sortie) sera :

I_C = α x I_E = 0,98 x 5 = 4,9mA

Si le transistor fonctionne avec de faibles courants d’émetteur (inférieurs à 1mA), on ne peut plus négliger le courant de saturation I_CBo car le courant de collecteur est aussi très faible.

Pour tenir compte de ce courant, la formule précédente doit être modifiée ; ainsi, pour déterminer le coefficient α, il suffira de soustraire du courant de collecteur, le courant de saturation I_CBo et en faire le rapport avec le courant d’émetteur :

α = (I_C - I_CBo)/I_E

Par analogie, pour déterminer le courant de collecteur, en partant du courant d’émetteur, il suffira de tenir compte de I_CBo :

I_C = α x I_E + I_CBo

Si par exemple I_CBo = 5µA, α = 0,98 et I_E = 0,1mA = 100µA nous aurons :

I_C = 0,98 x 100 + 5 = 98 + 5 = 103µA

C’est la valeur du courant total de collecteur qui est plus grand que I_E. Dans ces conditions, si l’on négligeait le courant de saturation I_CBo on trouverait un α plus grand que 1, ce qui ne peut pas être. On aurait en effet α = 103 : 100 = 1,03 environ.

Il nous faut maintenant faire une remarque fondamentale en ce qui concerne le fonctionnement du transistor. Nous avons dit au début de cette leçon, qu’un transistor était un dispositif qui avait la propriété d’amplifier : or nous voyons au contraire que le courant de sortie, c’est-à-dire I_C est toujours inférieur au courant d’entrée I_E. Il nous vient donc à l’esprit la question suivante : comment un transistor peut-il amplifier, si le courant qu’il fournit est toujours plus faible que celui qui est utilisé pour le commander  ?

Pour répondre à cette question, il suffit de faire la remarque suivante. La jonction émetteur-base est toujours polarisée dans le sens direct ce qui signifie qu’il suffit d’appliquer une tension très faible entre l’émetteur et la base, pour faire circuler un fort courant I_E : par exemple, pour obtenir un courant I_E de 5mA, nous avons supposé qu’il suffisait d’une tension V_EB de 0,1 V environ (figure 6).

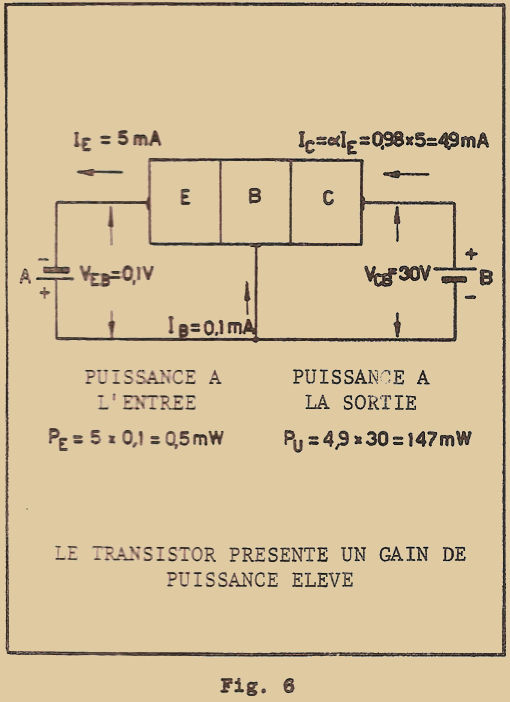
Dans ces conditions, dans le circuit du collecteur, nous aurons un courant I_C dont la valeur sera, pour un α = 0,98, de 4,9mA. La jonction collecteur-base est par contre polarisée en sens inverse, et peut donc supporter des tensions relativement élevées ; nous pouvons supposer par exemple que la tension V_CB est de 30 V.

Ceci signifie donc, que pour obtenir un courant de 4,9mA dans le circuit du collecteur, il faut fournir à l’émetteur, une puissance de :

5mA x 0,1 V = 0,5mW, c’est-à-dire un demi-milliwatt

Cette puissance est évidemment fournie par la pile A de la figure 6. La puissance qui est fournie par la pile B de polarisation du collecteur est au contraire de : 4,9mA x 30 V = 147mW, c’est-à-dire presque 300 fois plus grande que celle qui est fournie par la pile A.

Nous pouvons donc expliquer la propriété amplificatrice du transistor de la façon suivante : en fournissant à son circuit d’entrée, une puissance faible, celui-ci est capable de délivrer dans son circuit de sortie une puissance qui est quelques centaines de fois plus grande.

Ceci est dû exclusivement au fait que le transistor a la propriété de faire circuler dans son circuit de sortie qui est à haute tension, un courant qui est presque égal à celui qui circule dans son circuit d’entrée qui lui, est à basse tension. En effet, si la tension du collecteur était la même, ou plus faible que celle de l’émetteur, la puissance de sortie aurait été plus faible que celle délivrée au circuit d’entrée et on n’aurait eu aucune amplification de puissance.

Pour qu’un transistor amplifie, il faut donc que le circuit du collecteur fonctionne sous une tension beaucoup plus élevée que la tension sous laquelle fonctionne le circuit de l’émetteur.

Ainsi, si on applique à l’entrée d’un transistor, un signal de faible puissance, comme celui par exemple que peut délivrer un pick-up, on pourra prélever à la sortie le même signal, mais à une puissance beaucoup plus grande.

Nous pouvons faire une comparaison du type mécanique, en considérant par exemple le frein à air (pneumatique) : le chauffeur ne peut exercer une force suffisante pour bloquer les roues de son camion ; il appuie donc avec son pied, sur une pédale qui règle le flux de l’air comprimé. Sa commande est de faible puissance, mais elle est capable de délivrer une puissance très grande nécessaire pour arrêter le véhicule.

Le transistor se comporte donc comme cette pédale : commandé par une puissance faible, il est capable de délivrer une puissance beaucoup plus grande.

Il faut remarquer encore, que le circuit d’émetteur présente une faible résistance d’entrée (puisqu’il se comporte comme une diode polarisée dans le sens direct), tandis que le circuit du collecteur présente une résistance très grande (puisqu’il se comporte comme une diode polarisée en sens inverse).

De ce point de vue le transistor est un dispositif qui est capable de transférer un certain courant d’un circuit à faible résistance d’entrée, à un circuit de sortie à grande résistance. C’est cette propriété qu’ont utilisé les américains, pour former avec les termes "transfer" et "résistor", le mot "transistor".

3 – DISTINCTION ENTRE ÉMETTEUR ET COLLECTEUR

Si l’on regarde la figure 1, on peut se demander avec juste raison quelle est, des deux régions extrêmes, celle qui correspond à l’émetteur.

En effet, le transistor se présente d’une manière parfaitement symétrique en ce sens que les deux régions externes sont constituées par le même type de semi-conducteur, et que du point de vue principe de fonctionnement, il est absolument indifférent de considérer l’un ou l’autre comme émetteur ou comme collecteur.

En pratique, par contre, une telle symétrie n’existe pas à cause même de la fabrication du transistor. En effet, il faut faire de telle sorte que le coefficient d’amplification α soit le plus voisin de 1.

Ceci ne peut être obtenu, qu’en dopant différemment les semi-conducteurs qui deviendront l’émetteur et le collecteur.

On en déduit donc que la région qui doit devenir l’émetteur sera, celle qui sera la plus fortement dopée. D’autre part, pour des raisons de dissipation de la chaleur développée à l’intérieur du transistor, la jonction collecteur-base (comme nous le verrons plus tard) est en général de section plus grande que celle d’émetteur-base, ce qui est une autre raison pour rompre la symétrie.

Le manque de symétrie est plus prononcé dans un transistor dont le α est plus voisin de 1, et moins prononcé dans un transistor qui a un α faible

Ainsi, si par erreur de branchement, on intervertit les 2 extrémités collecteur et émetteur, le transistor pourra encore fonctionner plus ou moins bien. Si le transistor a un coefficient α élevé, une telle interversion donnera un α très faible par rapport à sa valeur normale, et le transistor fonctionnera moins bien évidemment.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 6^ème LEÇON THÉORIQUE

1 – La caractéristique V-I d’une diode exprime le courant dans la diode en fonction de la tension appliquée, dans le sens direct ou dans le sens inverse.

2 – Le courant inverse d’une diode correspond aux valeurs des flux des porteurs minoritaires.

3 – La tension de Zener est la valeur particulière de la tension pour laquelle le courant inverse d’une diode prend des valeurs très élevées.

4 – Dans l’effet Zener, l’augmentation de la concentration des porteurs minoritaires, due à la création de paires électron-trou, est provoqué par le champ électrique intense qui règne dans la zone de la barrière.

L’effet d’avalanche est dû par contre aux électrons qui franchissent la barrière à une très grande vitesse.

5 – On appelle diode de Zener, ou diode Zener, une diode à jonction réalisée pour exploiter l’effet Zener, et utilisable comme stabilisatrice de tension.

6 – Une diode à jonction qui fonctionne avec des tensions inverses ne dépassant pas la valeur de Zener, se comporte comme un condensateur, parce que dans ces conditions, la zone de la barrière, privée de charges libres, peut être considérée comme un diélectrique, tandis que les deux autres régions voisines forment les deux armatures.

7 – L’utilisation d’une diode à jonction à la place d’un condensateur variable classique présente l’avantage de pouvoir faire varier la capacité (entre certaines limites) d’une façon purement électronique, en agissant sur la tension inverse de polarisation : l’inconvénient est d’obtenir une capacité non "pure", car elle se présente comme un condensateur ayant en parallèle une résistance (à cause du courant inverse).

8 – La limite du courant direct d’une diode à jonction fonctionnant comme redresseuse est donnée par les dimensions de la jonction, tandis que la limite de la tension inverse est donnée par la tension de Zener.

9 – En observant la caractéristique d’une diode, on peut déterminer rapidement s’il s’agit d’une diode à jonction ou d’une diode à pointes : dans le premier cas (jonction) la caractéristique inverse est pratiquement horizontale, dans le second cas (pointes) elle est rapidement descendante.

---

EXERCICES DE RÉVISION SUR LA 7^ème LEÇON THÉORIQUE

1 – Comment est formé un transistor  ?

2 – Par quoi le fonctionnement d’un transistor NPN se différencie-t-il d’un transistor PNP  ?

3 – Comment doit-on polariser les deux jonctions d’un transistor  ?

4 – Qu’appelle-t-on courant résiduel I_CBo et quel est son ordre de grandeur par rapport au courant normal de collecteur  ?

5 – De quoi dépend le courant de collecteur  ?

6 – Comment définit-on le coefficient d’amplification en courant α et quelles sont ses valeurs courantes dans la pratique  ?

7 – Quels sont les procédés technologiques utilisés pour obtenir un α pratiquement égal à 1, c’est-à-dire pour faire en sorte que le courant I_C soit de très peu inférieur au courant I_E  ?

8 – Comment doit-on comprendre la propriété amplificatrice d’un transistor  ?

9 – Quelle est la condition indispensable pour qu’un transistor puisse amplifier  ?

Fin de la leçon 7

---

LECON 8

1 – MONTAGES EN BASE COMMUNE ET ÉMETTEUR COMMUN

Dans la leçon précédente, nous avons vu le principe de fonctionnement du transistor, en montrant comment le courant du collecteur pouvait être commandé par le courant d’émetteur. Pour que le transistor puisse fonctionner de cette manière, il faut polariser sa jonction émetteur-base dans le sens direct et sa jonction collecteur-base dans le sens inverse en utilisant deux piles distinctes, comme je vous l’indique sur la figure 1.

Si l’on regarde attentivement un tel montage on peut remarquer que la connexion de base est commune au circuit du collecteur et à celui de l’émetteur. En effet, si l’on considère le transistor comme un simple dispositif à trois connexions, on peut voir comment le courant de collecteur sort de la pile de droite parcourt la connexion de collecteur, entre dans le collecteur et sort par la connexion de base pour revenir au pôle négatif de cette pile ; le sens du courant I_C est indiqué par la flèche.

De la même manière, si l’on considère le circuit de l’émetteur, on voit comment le courant d’émetteur sort de la pile de gauche, entre dans le transistor par la connexion de base et sort par celle de l’émetteur.

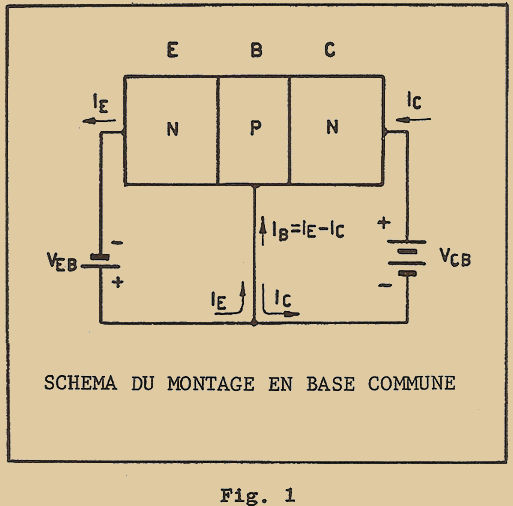
La liaison de base est ainsi parcourue en même temps par le courant de collecteur I_C et par celui de l’émetteur I_E. Étant donné que ces deux courants parcourent cette connexion en sens inverse, le courant de base réel, sera donné par leur différence, c’est-à-dire que l’on aura : I_B = I_E – I_C ; comme nous l’avons déjà vu, I_B sera très faible, étant donné que I_C est très peu différent de I_E.

Cette façon de brancher le transistor est appelé "Montage en base commune", puisque la connexion de base est commune aux circuits d’entrée et de sortie. Étant donné encore qu’en général, cette connexion de base est reliée à la masse, on dit aussi que le transistor est monté avec la BASE à la MASSE.

Pour faire fonctionner un transistor, on peut encore le monter selon le schéma de la figure 2. On polarise encore avec une pile et toujours dans le sens direct, la jonction émetteur-base, tandis que la jonction collecteur-base est polarisée, comme à l’habitude, en sens inverse, en reliant la pile entre le collecteur et l’émetteur au lieu de la relier entre le collecteur et la base comme c’était le cas à la figure 1.

Avec un tel schéma, la liaison de l’émetteur est commune aux circuits des deux piles car elle est parcourue et par le courant du collecteur et par le courant de la base, comme indiqué sur la figure 2 par les flèches.

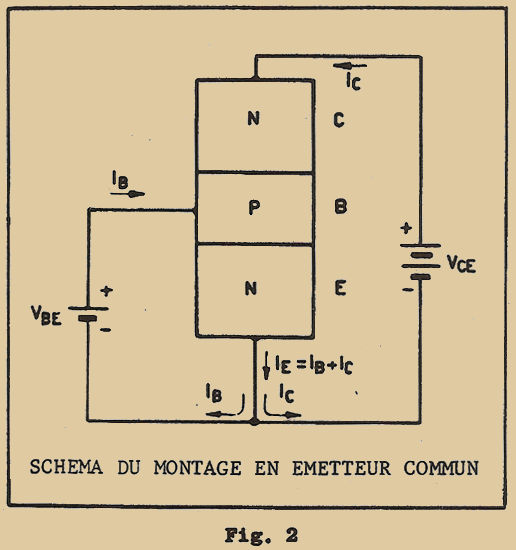
Le courant complexe dans la liaison de l’émetteur sera alors la somme des courants de collecteur et de la base, puisqu’ils circulent tous les deux dans le même sens, et l’on aura :

I_E = I_C + I_B

Par analogie avec le circuit précédent, le montage de la figure 2 sera dit "Montage en Émetteur Commun" ou "Émetteur à la masse", étant donné que maintenant la liaison de l’émetteur est commune au circuit d’entrée (qui est maintenant la base, au lieu d’être l’émetteur) et au circuit de sortie (qui est encore le collecteur).

Le fonctionnement du transistor en montage émetteur commun est un peu différent de celui que nous avons vu dans la dernière leçon, en ce sens que le circuit d’entrée est maintenant celui de la base au lieu d’être celui de l’émetteur, c’est-à-dire que maintenant le courant de collecteur sera commandé par celui de la base. Pour l’instant, nous étudierons uniquement le fonctionnement du transistor dans ce montage, comme nous l’avons fait pour la base commune. Les avantages et les inconvénients de ces deux schémas seront illustrés ultérieurement, lors de l’étude des circuits amplificateurs.

1 – 1 POLARISATION DU COLLECTEUR

Dans ce montage en émetteur commun, la tension du collecteur est appliquée entre le collecteur et l’émetteur avec une polarité telle qu’elle rende la jonction collecteur-base polarisée en sens inverse.

Si l’on considère un transistor NPN, on aura le pôle positif de la pile branché sur le collecteur comme on peut le voir sur la figure 3.

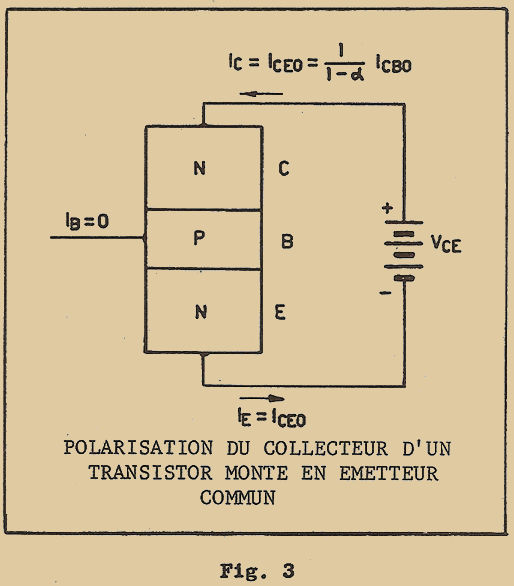
Dans le circuit, il circulera alors un courant de collecteur que l’on appelle I_CEo (se dit "i, cé, é, zéro") et qui indique le courant qui circule entre le collecteur et l’émetteur, lorsque le courant de base est nul (en effet, la base n’est pas reliée car elle est "en l’air", et dans sa connexion, il ne peut circuler aucun courant.

Ce courant de collecteur est analogue à celui de I_CBo que l’on avait dans le cas du montage en base commune, mais on peut voir rapidement que I_CEo n’est plus simplement le courant résiduel de la jonction collecteur-base, mais qu'il est beaucoup plus grand.

Pour comprendre ceci, il suffit de considérer que la tension V_CE fournie par la pile, se répartit entre les deux jonctions qui se trouvent disposées en série.

On peut penser alors, remplacer le transistor par deux diodes à jonction (figure 4), l’une d’elle indiquée par D_CB représentant la jonction collecteur-base et l’autre indiquée par DBE, et symbolisant la jonction base-émetteur. Ces diodes seront obligatoirement reliées en série et disposées l’une en sens inverse de l’autre comme on peut le voir sur la figure 4-a.

Ainsi la jonction collecteur-base est parcourue par le courant dans le sens N-P, tandis que la jonction base-émetteur est parcourue dans le sens P-N. Si les diodes sont disposées de cette façon, la diode D_CB sera polarisée en sens inverse (comme l’est la jonction collecteur-base), puisque la cathode est reliée au pôle positif de la pile, tandis que la diode DBE est polarisée dans le sens direct, étant donné que la cathode est reliée au pôle négatif de la pile.

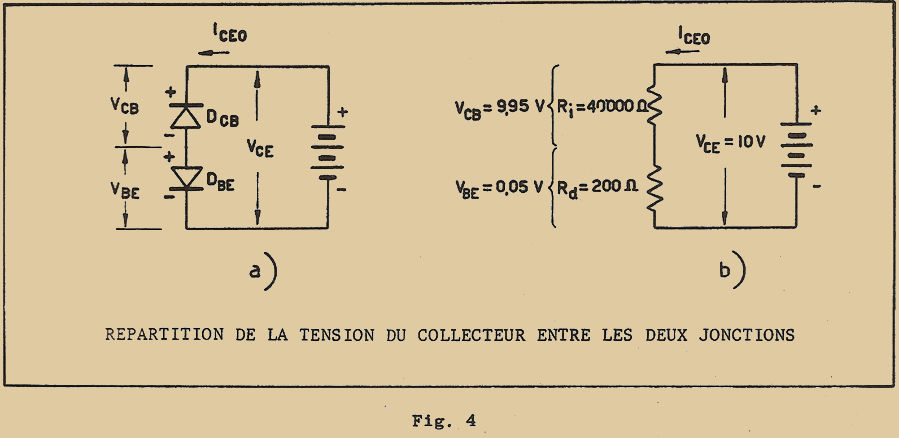
La tension V_CE se répartit donc entre deux tensions : V_CB aux bornes de la diode D_CB et V_BE aux bornes de la diode DBE. Pour déterminer ces deux tensions on peut encore remplacer les deux diodes par leur résistance interne, qui ont des valeurs très différentes ; en effet, la diode D_CB étant polarisée en sens inverse a une résistance R_i très élevée ; par contre, la diode DBE étant polarisée dans le sens direct, présente une résistance directe R_d très faible.

Prenons un exemple, et supposons que la tension V_CE soit de 10 V, que R_i soit de 40.000 Ω et que R_d, soit de 200 Ω (c’est-à-dire 200 fois plus petite que R_i). Il en résulte alors le schéma de la figure 4-b où R_i et R_d se comportent comme des répartiteurs de tension.

La tension V_BE aux bornes de R_d sera donnée par la relation :

V_BE = V_CE R_d/(R_d + R_i ) = 10 200/(200+40.000) = 0,05 V environ

Aux bornes de R_i la tension sera :

V_CB = V_CE – V_BE = 10 – 0,05 = 9,95 V

Il résulte de ce simple calcul que la tension de 10 V donnée par la pile n’est pas appliquée intégralement à la jonction collecteur-base : une faible partie de cette tension se retrouve aux bornes de la jonction base-émetteur, et polarise ainsi dans le sens direct cette jonction (voir figure 5-a).

Ceci signifie donc que la barrière de potentiel existant entre le collecteur et la base se trouve accrue seulement de 9,95 V, au lieu de 10 V, si l’on reprend l’exemple ci-dessus. Au même moment, la barrière de potentiel qui existe entre la base et l’émetteur se trouve réduite de 0,05 V comme on peut le voir sur la figure 5-b ; où la ligne en pointillés représente la barrière de potentiel existant en l’absence de polarisation, tandis que la ligne en traits pleins représente la même barrière de potentiel modifiée par l’application de la tension V_CE.

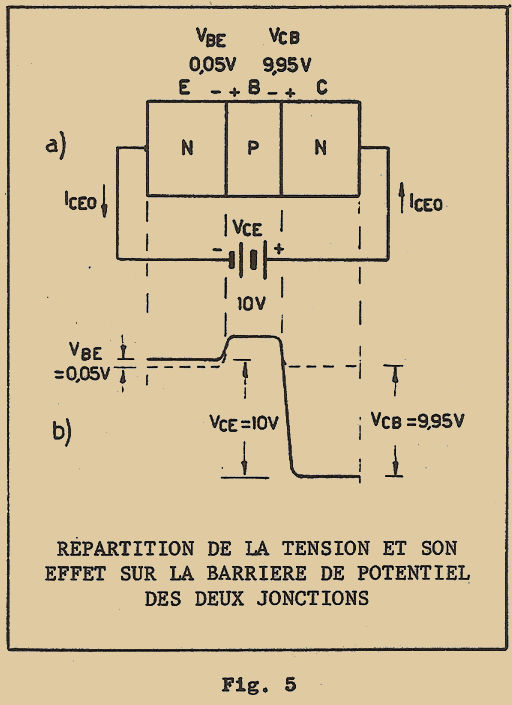
Nous pouvons maintenant refaire le raisonnement établi en son temps sur la polarisation simultanée des 2 jonctions du transistor en base commune (revoir la leçon précédente), et conclure ce qui suit :

Si l’on applique une tension entre le collecteur et l’émetteur, une faible partie de celle-ci polarise en sens direct la jonction base-émetteur, ce qui provoque de la part de l’émetteur, l’émission d’une certaine quantité d’électrons qui diffusent dans la base et en grande partie atteignent le collecteur.

Le courant de collecteur ne sera donc pas uniquement constitué par le courant résiduel I_CBo mais aussi par le courant dû à l’émission des électrons par l’émetteur.

Si l’on veut déterminer de combien le courant I_CEo est plus grand que le courant I_CBo, il suffira d’utiliser la formule que nous avons vue dans la leçon précédente et qui est valable dans tous les cas :

I_C = α I_E + I_CBo

Il faut se rappeler que dans ce cas, I_E est nécessairement égal à I_C puisque I_B est nul (la base n’est pas reliée) et aussi que cette valeur particulière de I_C est appelée I_CEo.

En remplaçant alors I_C et I_E par I_CEo dans la formule précédente, on trouve après une transformation algébrique simple :

I_CEo = 1/(1- α) I_CBo

Pour avoir une idée sur l’augmentation de I_CEo par rapport à I_CBo supposons que α soit égal à 0,98 et que I_CBo soit de 5µA. On aura alors :

I_CEo = 1/(1- 098) I_CBo = 1/0,02 I_CBo = 50 I_CBo = 50 x 5 = 250µA,

c’est-à-dire que I_CEo qui en résulte est 50 fois plus grand que le courant I_CBo que l’on aurait si le transistor était monté en base commune.

La valeur de 1/(1- α) dépend naturellement de la valeur de α du transistor considéré et sera d’autant plus grande que plus grand sera α ; par exemple, si α est compris entre 0,95 et 0,995, on trouve que I_CEo sera de 20 à 200 fois plus grand que I_CBo.

1 – 2 POLARISATION DE LA BASE ET COEFFICIENT D’AMPLIFICATION "BETA"

Avec le montage émetteur commun, le courant de collecteur peut encore être commandé en agissant sur la hauteur de la barrière de potentiel existant entre la base et l’émetteur.

Tandis que dans le cas du montage en base commune, la jonction base-émetteur était polarisée dans le sens direct en appliquant une tension négative sur l’émetteur, on doit appliquer maintenant, une tension positive sur la base. En effet, pour polariser la jonction on peut, soit rendre l’émetteur négatif par rapport à la base, soit rendre positive la base par rapport à l’émetteur. Le schéma du circuit sera donc celui de la figure 2 (il est évident par contre, que si l’on utilise un transistor PNP, les tensions qu’il faudra appliquer au collecteur ou à la base devront être négative au lieu d’être positives).

Si l’on rend la base positive, on diminue la hauteur de la barrière de potentiel de la jonction base-émetteur et on augmente ainsi le flux des électrons émis par l’émetteur et captés par le collecteur.

Si l’on considère les courants, on peut dire qu’en augmentant la tension de polarisation V_BE de la base, on augmente le courant de base I_B et proportionnellement, il y a augmentation du courant de collecteur I_C. En d’autres termes, le courant I_C est commandé par le courant de base.

Ainsi, dans le cas du montage en émetteur commun, on peut définir un coefficient d’amplification de courant comme étant un rapport entre le courant de collecteur (c’est-à-dire le courant de sortie) et le courant de commande qui le détermine, c’est-à-dire dans notre cas le courant de base (au lieu que ce soit le courant d’émetteur).

Étant donné que le courant résiduel I_CEo est beaucoup plus grand que le courant I_CBo que l’on avait en montage base à la masse, on ne peut plus le négliger devant les valeurs normales du courant du collecteur, il faut donc en tenir compte.

Par analogie avec ce qui a été dit dans le cas du montage en base commune, on appellera "coefficient d’amplification de courant", le rapport entre le courant collecteur I_C diminué du courant résiduel I_CEo et le courant de base I_B.

Ce coefficient est appelé BETA (seconde lettre de l’alphabet grec dont le symbole est "β") et est exprimé par la relation suivante :

β = (I_C-I_CEo)/I_B

(il faut indiquer que certains auteurs appellent ce coefficient α ; pour le distinguer alors du coefficient d’amplification en montage base à la masse, on l’écrit α B pour le montage base à la masse, et α E pour celui en émetteur commun).

Pour se rendre compte des valeurs de β que l’on trouve normalement pour les transistors et leurs relations avec les valeurs de α, il suffira de faire le raisonnement simple suivant :

Dans le cas du montage en émetteur commun, le courant d’émetteur est toujours de très peu supérieur à celui du collecteur, de par le mécanisme de fonctionnement même des transistors comme nous l’avons vu dans la dernière leçon.

Le courant de base est toujours donné par la différence entre I_E et I_C et a donc une valeur très faible par rapport à I_C. On se doute bien, que les valeurs de β qui vont en résulter, seront beaucoup plus grandes que 1.

On peut en effet démontrer, par simple transformation algébrique, que β est lié à α (puisqu’au fond, il s’agit de deux coefficients relatifs à un même transistor branché de deux façons différentes) et il est donné par :

β = α/(1- α)

Cette formule permet ainsi de calculer le coefficient d’amplification de courant d’un transistor monté en émetteur commun lorsque l’on connait la valeur du coefficient d’amplification de courant en montage base commune.

Par exemple, pour un transistor qui a un α = 098, en montage en émetteur commun on aura un coefficient d’amplification :

β = 0,98/(1- 0,98) = 0,98/0,02 = 49

On peut voir ainsi la grande différence qu’il y a entre les deux types de montage : tandis qu’en base commune le coefficient d’amplification est toujours inférieur à 1, dans le montage en émetteur commun ce coefficient prend des valeurs beaucoup plus grandes, c’est-à-dire que le transistor fonctionne véritablement comme amplificateur de courant. Ceci signifie qu’il suffit de faibles valeurs du courant de commande (courant de base) pour obtenir des valeurs élevées du courant de collecteur.

En effet, le courant de collecteur, qui en l’absence de polarisation de la base (courant de base I_B nul) prend la valeur I_CEo (courant résiduel), augmente d’une valeur égale à β fois la valeur du courant que l’on fait circuler dans la base et qui est donc plusieurs dizaines de fois plus grand que I_B. En termes mathématiques, le courant de collecteur I_C est donné par la formule :

I_C = β I_B + I_CEo

Ainsi, si dans un transistor dont le β = 49 et I_CEo = 250µA on fait circuler dans la base un courant I_B de 100µA par exemple, le courant de collecteur prendra la valeur :

I_C = 49 x 100 + 250 = 4900 + 250 = 5150µA = 5,15mA

Dans le montage en base commune, pour obtenir cette valeur de courant de collecteur, on aurait eu besoin d’un courant de commande (courant d’émetteur) du même ordre de grandeur que I_C (et même légèrement supérieur à 5,15mA), c’est-à-dire d’un courant beaucoup plus grand que celui en émetteur commun.

Les valeurs de β que l’on rencontre en pratique pour les transistors classiques de faible et de moyenne puissance (comme ceux utilisés dans les récepteurs radio), varient de 20 à 200 selon les types. Ces valeurs correspondent à des valeurs de α comprises entre 0,95 et 0,995 environ.

1 – 3 COMPARAISON ENTRE LES DEUX TYPES DE MONTAGES

De ce qui vient d’être vu, il apparaît évident que le transistor présente un gain de courant en émetteur commun, beaucoup plus grand que celui en base commune. Ceci signifie donc que l’on peut obtenir un courant de collecteur donné, à l’aide d’un courant de commande très faible.

Ainsi, pour fixer les idées, on peut dire par exemple, que pour un transistor préamplificateur basse fréquence, le courant de commande de base (montage en émetteur commun), est de l’ordre de quelques dizaines deµA, tandis que pour le même transistor en montage base commune le courant de commande (courant d’émetteur), doit être de l’ordre de quelques mA.

On peut ainsi considérer que le gain de puissance exprimé comme le rapport entre la puissance fournie par la pile du collecteur à celle fournie par la pile de polarisation de la base, est nettement plus élevé avec l’émetteur à la masse. Pour donner un exemple on peut reprendre le cas considéré dans la leçon précédente relatif au montage en base commune.

On suppose que pour faire circuler dans la base, un courant de commande de 100µA (= 0,1mA) le transistor nécessite une tension de polarisation de 0,1 V ; la puissance fournie par la pile de polarisation de la base (pile 1 de la figure 6) sera donc égale à :

0,1 V x 0,1mA = 0,01mW

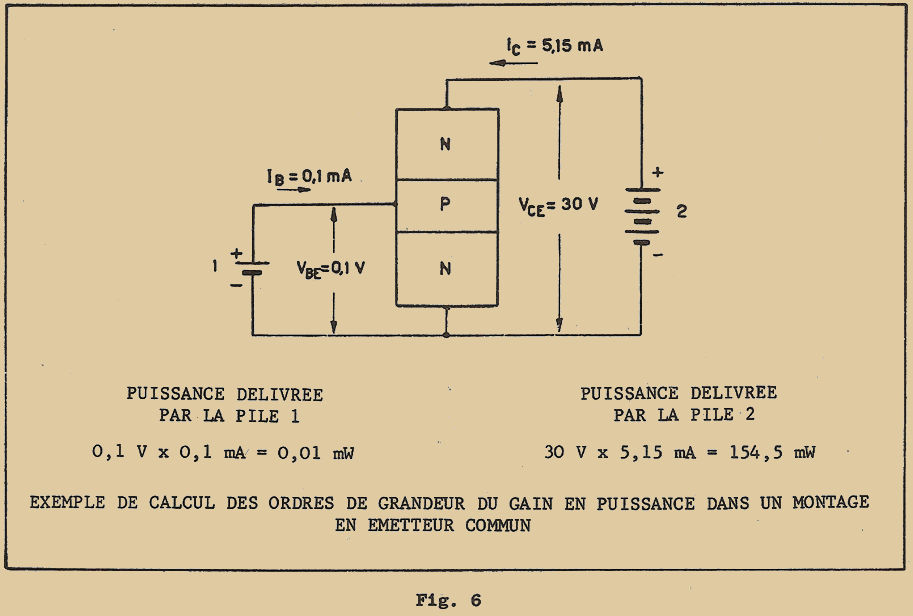
Avec un tel courant de base, on a vu que l’on obtenait un courant de collecteur égal à 5,15mA. Si l’on suppose d’autre part, que la tension de polarisation du collecteur est de 30 V, la puissance délivrée sera :

30 V x 5,15mA = 154,5mW

Le gain en puissance est donc : 154,5/0,01 = 15.000 environ. Dans le cas du montage en base commune, on avait trouvé un gain de 300 seulement.

A ce gros avantage du montage en émetteur commun, il y a par contre un inconvénient assez sensible qui est celui d’un grand courant résiduel.

Nous avons déjà vu que ce courant I_CEo est beaucoup plus grand que le courant résiduel I_CBo relatif au cas du montage en base commune et nous avons dit que I_CEo était 1/(1- α) fois plus grand que I_CBo. Maintenant que nous avons défini le coefficient d’amplification β nous pouvons trouver d’une façon très simple, la valeur de I_CEo.

Considérons en effet le schéma de la figure 7, où l’on n’applique au transistor que la tension de collecteur V_CE.

Dans ces conditions, la jonction collecteur-base est polarisée en sens inverse et est ainsi traversée par le courant résiduel I_CBo (courant inverse de la diode collecteur-base).

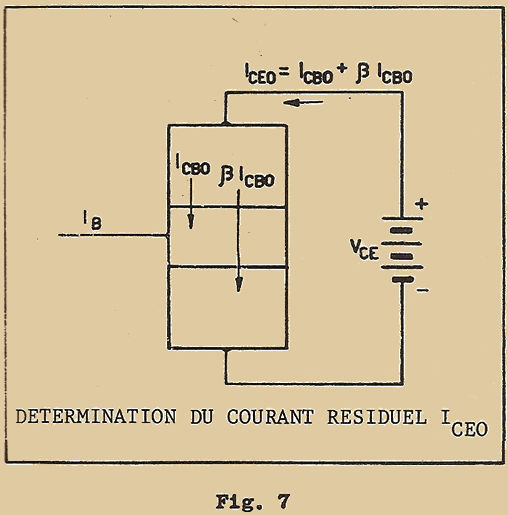
Ce courant ne peut revenir à la pile par la liaison de base comme dans le cas du montage en base commune, puisque celle-ci est "en l’air". Ainsi, I_CBo doit obligatoirement traverser la jonction base-émetteur, mais il se comporte alors comme un courant de commande et provoque une augmentation du courant de collecteur égal à β fois la valeur de ce même courant I_CBo. En conclusion, le courant I_CEo sera constitué par le courant I_CBo et par un courant égal à β fois I_CBo.

I_CEo = I_CBo β I_CBo = (β + 1) I_CBo

Ainsi donc, le courant résiduel du collecteur dans le cas d’un montage en émetteur commun est β + 1 fois plus grand que le courant résiduel que l’on aurait en montage base commune.

Si l’on tient compte de la relation qui lie β et α, on voit facilement que la valeur de β+1 est égale à 1/(1- α) . Etant donné aussi, que la valeur de β est toujours beaucoup plus grande que 1, la différence entre β et β + 1 est faible. C’est pour cette raison, que l’on dit couramment que I_CEo est environ β fois plus grand que I_CBo.

Pour résumer un peu tout ce que nous venons de voir, nous allons reporter dans le tableau ci-dessous, les valeurs que nous avons trouvées dans les exemples précédents, étant bien entendu que ce sont des ordres de grandeur, qui peuvent varier d’un type de transistor à l’autre.

	B. Com.	Em. Com.
Coefficient d'amplification de courant	α = 0,98	β = 49
Coefficient d'amplification de puissance	300	15000
Courant de collecteur	IC = 5mA	IC ~5mA
Courant de commande	IE = 5mA	IB = 0,1mA
Courant résiduel	ICB0 = 5µA	ICE0 = 250µA

2 – TRANSISTORS À JONCTION NPN ET PNP ET LEUR SYMBOLE GRAPHIQUE

Dans les schémas que nous avons vus jusqu’ici, nous avons toujours représenté le transistor de façon schématique d’après sa véritable constitution physique, c’est-à-dire par trois rectangles figurant les trois régions du semi-conducteur qui le constituent. Dans les schémas électriques des montages à transistors, on représente le transistor par un symbole graphique qui indique d’une manière conventionnelle, s’il s’agit d’un transistor du type NPN ou d’un PNP. De nombreux signes graphiques ont été utilisés dans le passé, mais actuellement, les symboles représentés à la figure 8 ont été normalisés. Un trait épais représente le bloc du semi-conducteur d’où partent trois connexions - D’une part, un trait perpendiculaire au trait épais, indique la liaison de base ; d’autre part on remarque deux traits inclinés qui représentent les liaisons de l’émetteur et du collecteur. Pour distinguer l’émetteur du collecteur, le premier porte une flèche, dont la direction a pour rôle d’indiquer s’il s’agit de transistor du type NPN ou PNP.

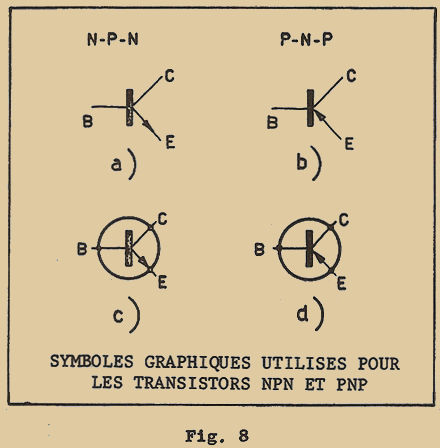
Le choix de la direction de la flèche est fait de telle sorte qu’elle indique la direction de circulation du courant direct (dans le sens conventionnel et non pas dans le sens électronique) de la jonction émetteur-base. En se rappelant alors qu’une jonction conduit dans le sens P-N il est facile de déterminer que la flèche sera tournée vers l’extérieur dans le cas d’un transistor NPN (c’est-à-dire de la base, qui est du type P vers l’émetteur qui est du type N) tandis que dans le cas d’un transistor PNP, elle sera tournée vers le trait épais (c’est-à-dire de l’émetteur, qui est du type P, vers la base qui est du type N). Les deux cas sont représentés respectivement sur les figures 8-a et 8-b.

Dans certains cas ces symboles graphiques sont entourés par un cercle et se présentent comme indiqués sur les figures 8-c et 8-d qui indiquent respectivement les types NPN et PNP.

Dans toutes les études que nous avons faites jusqu’à présent, nous avons toujours considéré que le transistor était du type NPN : mais il est bien entendu que tout reste valable s’il s’agit du type PNP, en prenant la précaution d’inverser les tensions de polarisation des électrodes.

Pour résumer ce qui vient d’être dit, je vous ai dressé un tableau où se trouvent réunis les différents montages possibles (quatre cas) et à la figure 9 je vous indique les schémas correspondants.

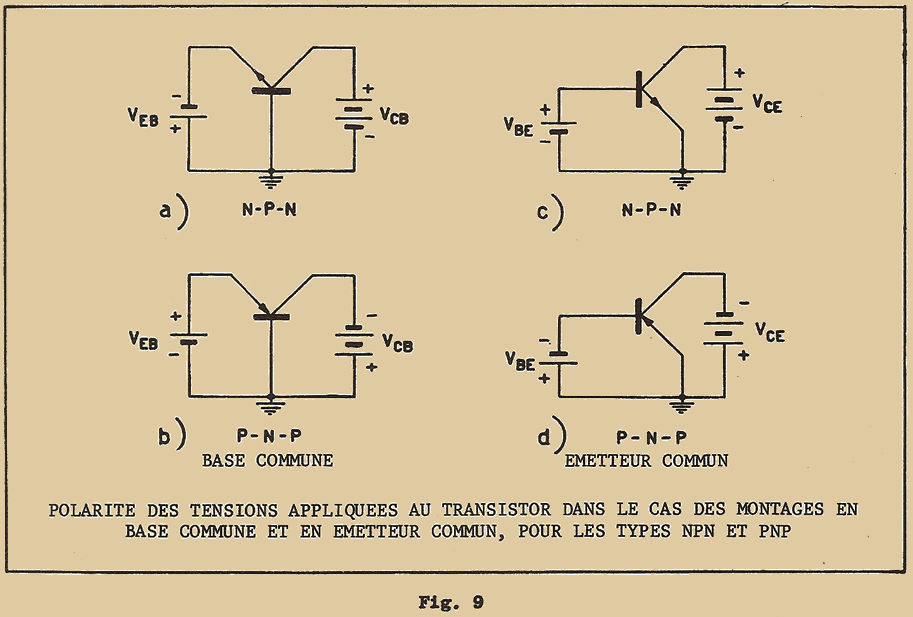
1. Montage en base commune – Transistor NPN (figure 9-a). Tension de collecteur V_CB : positive. Tension d’émetteur V_EB : négative.

2. Montage en base commune – Transistor PNP (figure 9-b). Tension de collecteur V_CB : négative. Tension d’émetteur V_EB : positive.

3. Montage en émetteur commun – Transistor NPN (figure 9-c). Tension de collecteur V_CE : positive. Tension e base V_BE : positive.

4. Montage en émetteur commun – Transistor PNP (figure 9-d). Tension de collecteur V_CE : négative Tension e base V_BE : négative.

Dans ces schémas, vous remarquerez que la tension de collecteur est toujours positive dans le cas des transistors NPN et négative dans le cas des transistors PNP, tandis que la tension de l’électrode de commande (base et émetteur respectivement dans les deux types de montage) a sa polarité opposée à celle du collecteur en base commune, et la même que celle du collecteur dans le montage en émetteur commun.

3 – TRANSISTORS À POINTES

Les premiers transistors qui apparurent ne furent pas à jonction comme ceux que nous avons étudié maintenant, mais du type à pointes. Comme de tels transistors ont pratiquement disparu actuellement (en tous les cas dans les récepteurs radio) et ont été remplacés par des transistors jonction de qualité supérieure, ils n’en présentent pas moins un intérêt historique. Nous en parlerons brièvement comme simple rappel

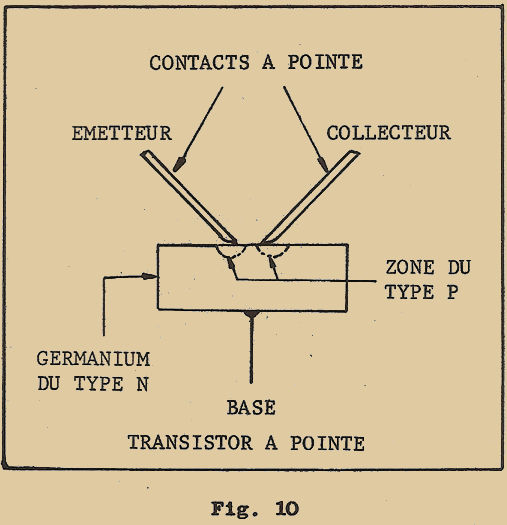
Comme je vous l’indique sur la figure 10, le transistor à pointes est constitué par un bloc de germanium du type N, sur lequel viennent s’appuyer deux pointes métalliques, chacune d’entr’elles formant avec le germanium une diode à pointes.

Le fonctionnement du transistor à pointes peut être expliqué en reprenant la théorie déjà exposée et qui traitait des diodes à pointes, c’est-à-dire en admettant que dans le voisinage immédiat de chacune des pointes il se forme dans le germanium N, une zone P, par l’intermédiaire d’une formation, analogue à celles des diodes.

De cette manière, il se forme deux petites jonctions et le fonctionnement du transistor à pointes peut être comparé à celui d’un transistor du type PNP.

Dans la réalisation pratique, les deux pointes sont placées à une distance très faible l’une de l’autre, à peine 50 µ, et sont constituées par des fils très fins de tungstène qui appuient avec une légère pression sur la surface du germanium. Dans certains types de transistors, les deux pointes peuvent être de métal différent ; ainsi par exemple, on utilise le bronze phosphoreux pour former la pointe qui doit fonctionner comme collecteur.

Les défauts principaux des transistors à pointes sont les suivants : instabilité des contacts, variation des caractéristiques du transistor dans le temps (le transistor "vieillit" comme on dit) et bruit de fond important ; valeurs du courant résiduel du collecteur élevées, surtout lorsque le transistor est utilisé dans un montage en émetteur commun ; courants de collecteur faibles à cause de la surface de contact réduite, ce qui limite la puissance de sortie.

Pour toutes ces raisons, le transistor à pointes a été pratiquement abandonné dans les circuits radio, dès que l’évolution de la technique de fabrication des transistors à jonction a permis d’atteindre avec ces derniers les fréquences élevées de fonctionnement, qui avaient été pendant un certain temps, le domaine exclusif des transistors à pointes.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 7^ème LEÇON THÉORIQUE

1 – Un transistor est formé par un bloc de germanium d’un type donné, placé entre deux blocs de type opposé.

2 – La différence de fonctionnement d’un transistor du type NPN par rapport à un transistor du type PNP réside uniquement dans la polarité de la tension de polarisation.

3 – Pour un fonctionnement correct d’un transistor, sa jonction émetteur-base devra toujours être polarisée dans le sens direct, tandis que la jonction collecteur-base devra toujours être polarisée en sens inverse.

4 – Le courant résiduel I_CBo est le courant qui traverse la liaison du collecteur, quand le courant qui traverse la liaison d’émetteur est nul. Il est environ mille fois plus faible que le courant normal de collecteur.

5 – Le courant de collecteur d’un transistor dépend exclusivement du courant que l’on fait circuler dans la liaison de son émetteur.

6 – Le coefficient d’amplification de courant α est défini comme le rapport entre le courant du collecteur et celui de l’émetteur ; en pratique la valeur α est comprise entre 0,950 et 0,995.

7 – Pour rendre la valeur du courant de collecteur aussi voisine que possible de la valeur du courant d’émetteur, on doit faire une base aussi mince que possible ainsi qu’un dopage élevé pour l’émetteur et très faible pour la base.

8 – On doit comprendre la propriété amplificatrice d’un transistor comme étant celle d’un certain dispositif qui est capable de délivrer à sa sortie, une puissance plus grande que celle utilisée pour le commander.

9 – La condition indispensable pour qu’un transistor puisse fonctionner comme amplificateur de puissance est que la tension appliquée sur son collecteur soit plus grande que celle que l’on applique sur l’émetteur.

---

EXERCICES DE RÉVISION SUR LA 8^ème LEÇON THÉORIQUE

1 – Quelle est la différence qui existe entre le montage en base commune et celui en émetteur commun (préciser quels sont les courants de commande dans l’un et l’autre montage  ?

2 – Pourquoi dans un transistor déterminé, le courant résiduel I_CEo est-il toujours plus grand que le courant I_CBo  ?

3 – Par quoi est donné le coefficient d’amplification de courant β  ?

4 – Entre quelles valeurs extrêmes, peut varier le coefficient β dans les transistors du commerce  ?

5 – Quels sont les avantages et les inconvénients du montage émetteur commun par rapport à celui en base commune  ?

6 – Comment peut-on distinguer la connexion de l’émetteur de celui du collecteur en observant le symbole graphique d’un transistor  ?

7 – Par quoi se différencie le symbole graphique d’un transistor PNP d’un transistor NPN  ?

8 – Quelle est la polarité de la tension du collecteur dans le cas d’un transistor NPN et dans celui d’un PNP  ?

9 – Quelle est la polarité de la tension appliquée à l’électrode de commande d’un transistor par rapport à celle qui doit être appliquée au collecteur  ?

Fin de la leçon 8

---

LECON 9

1 – COURBES CARACTÉRISTIQUES DES TRANSISTORS

Lors de l’étude des diodes, nous avons vu que nous pouvions représenter leurs propriétés, de façon simple et complète en déterminant les courbes caractéristiques V – I, qui expriment le courant dans la diode lorsque l’on fait varier la tension appliquée à ses bornes. En d’autres termes, d’après la courbe caractéristique on peut connaître la valeur du courant dans la diode quand on applique à ses bornes une tension déterminée, directe ou inverse.

Les propriétés des Transistors peuvent aussi être exprimées de façon analogue, à l’aide de courbes caractéristiques, mais la représentation est beaucoup plus complexe.

Tout d’abord, on doit remarquer que le transistor peut être branché de deux façons différentes, il faut donc s’attendre, étant donné que ses propriétés ne sont plus les mêmes, qu’il sera nécessaire et même indispensable d’avoir deux représentations différentes, une pour le montage en base commune et l’autre pour le branchement en émetteur commun.

D’autre part, dans le cas de la diode il n’y avait que deux grandeurs en jeu (figure 1-a) et il suffisait d’une seule courbe caractéristique pour les représenter ; dans le cas du transistor, nous avons quatre grandeurs (figure 1-b) qui indépendamment du montage (base commune ou émetteur commun), peuvent être considérées comme formant deux grandeurs liées (paires). La première paire, correspond au circuit d’entrée (circuit de commande du transistor), elle est constituée par la tension V_e appliquée entre l’électrode de commande et l’électrode commune, et par le courant I_e qui traverse alors cette électrode de commande. L’autre paire est constituée par la tension V_u appliquée entre l’électrode de sortie et celle qui est commune, et par le courant I_u qui traverse la liaison de l’électrode de sortie.

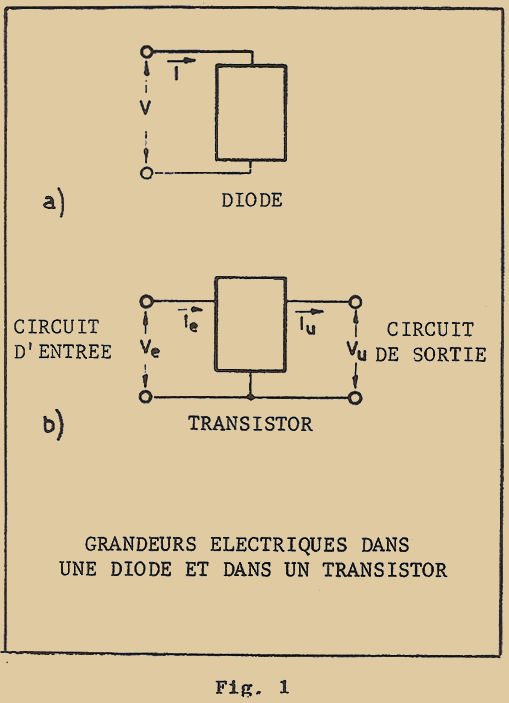
On voit donc que l’on peut représenter par exemple, d’une part les caractéristiques du circuit d’entrée et d’autre part celles du circuit de sortie.

En examinant par exemple ces dernières qui représentent les variations du courant de sortie I_u lorsque l’on fait varier la tension de sortie V_u, on peut noter tout de suite que le courant de sortie dépend aussi du courant d’entrée I_e, ou bien de la tension d’entrée V_e, puisque c’est elle qui détermine le courant I_e. Nous en déduisons donc que la courbe V_u – I_u ne sera pas unique comme dans le cas de la diode, mais qu’il y en aura autant que désiré, chacune d’elle étant caractéristique d’une valeur particulière du courant de commande I_e (ou de la tension V_e).

Les propriétés du circuit de sortie du transistor ne pourront donc être représentées de façon complète que si l’on trace différentes courbes V_u – I_u, chacune d’elle fonction de la valeur I_e (ou V_e) qui la détermine.

L’ensemble de ces courbes prend le nom de "Famille de courbes caractéristiques de sortie" et l’on dira que ces courbes ont comme Paramètre, le courant I_e ou la tension V_e suivant que telle ou telle des deux grandeurs d’entrée est choisie.

En conclusion, pour le circuit de sortie, nous pourrons avoir deux familles de courbes caractéristiques bien distinctes, une qui a pour paramètre le courant d’entée I_e, l’autre qui a pour paramètre la tension d’entrée V_e. Nous les appellerons "Courbes caractéristiques de sortie" ou "Caractéristique V_u – I_u".

De la même manière, nous pouvons prendre en considération les deux grandeurs I_e et V_e : en refaisant le même raisonnement, nous arriverons à la conclusion que les propriétés du circuit d’entrée d’un transistor, peuvent être représentées par deux familles de courbes caractéristiques différentes, suivant que l’on prend comme paramètre, le courant I_u ou la tension V_u. A ces familles de courbes, nous donnerons le nom de "Courbes caractéristiques d’entrée" ou "Caractéristiques V_e - I_e".

En combinant de façon différente les quatre grandeurs de la figure 1-b, nous pourrons obtenir d’autres familles de courbes caractéristiques. Par exemple, en considérant I_u et I_e et V_u et V_e, nous pouvons obtenir des courbes appelées "Caractéristiques mutuelles" nom qui provient du fait qu’elles représentent la dépendance de chacune des grandeurs de sortie, avec les grandeurs d’entrée de la même espèce (c’est-à-dire courant de sortie et courant d’entrée ou bien tension de sortie et tension d’entrée.

On obtient ainsi ce que l’on appelle les Caractéristiques mutuelles de courant ou Caractéristiques I_u – I_e qui peuvent avoir comme paramètre la tension V_u ou la tension V_e, et les Caractéristiques mutuelles de tension, ou caractéristiques V_u – V_e ayant comme paramètre le courant I_e ou le courant I_u.

Nous pouvons obtenir encore quatre autres familles de caractéristiques si nous considérons I_u – V_e et V_u – I_e. Celles-ci vont prendre le nom de Caractéristiques de Transfert et exprimeront la dépendance du courant et de la tension de sortie par rapport à la tension et au courant d’entrée.

Au total nous avons douze familles différentes de courbes caractéristiques qui sont les suivantes :

1. - Caractéristique de sortie V_u – I_u avec comme paramètre I_e
2. - Caractéristique de sortie V_u – I_u avec comme paramètre V_e
3. - Caractéristique d’entrée V_e – I_e avec comme paramètre I_u
4. - Caractéristique d’entrée V_e – I_e avec comme paramètre V_u
5. - Caractéristiques mutuelles de courant I_u – I_e avec comme paramètre V_e
6. - Caractéristiques mutuelles de courant I_u – I_e avec comme paramètre V_u
7. - Caractéristiques mutuelles de tension V_u – V_e avec comme paramètre I_e
8. - Caractéristiques mutuelles de tension V_u – V_e avec comme paramètre I_u
9. - Caractéristiques de transfert I_u – V_e avec comme paramètre I_e
10. - Caractéristiques de transfert I_u – V_e avec comme paramètre V_u
11. - Caractéristiques de transfert V_u – I_e avec comme paramètre V_e
12. - Caractéristiques de transfert V_u – I_e avec comme paramètre I_u

Ce sont toutes les caractéristiques possibles que l’on peut tracer, mais il suffit d’en donner seulement deux, pour représenter complètement les propriétés d’un transistor. Celles-ci seront choisies parmi celles qui contiennent les quatre grandeurs en présence, c’est-à-dire celles qui sont représentées à la figure 1-b. À partir de ces deux seules caractéristiques nous pourrons déduire les dix autres par des constructions graphiques simples. Le choix de l’une à l’autre caractéristique ne dépend uniquement que du circuit particulier que vous avez à étudier, ainsi un type de caractéristique peut être plus commode qu’un autre.

Dans les renseignements techniques donnés par le fabricant, figure souvent la caractéristique de sortie, avec comme paramètre, le courant d’entrée. Celle-ci est en général, accompagnée par une ou plusieurs autres caractéristiques.

Pour que vous compreniez mieux, je vais vous indiquer maintenant comment en pratique, on peut obtenir ces courbes, dans le cas du montage en base commune puis dans celui en émetteur commun.

A la figure 2, vous trouverez les grandeurs qui interviennent respectivement dans ces deux montages.

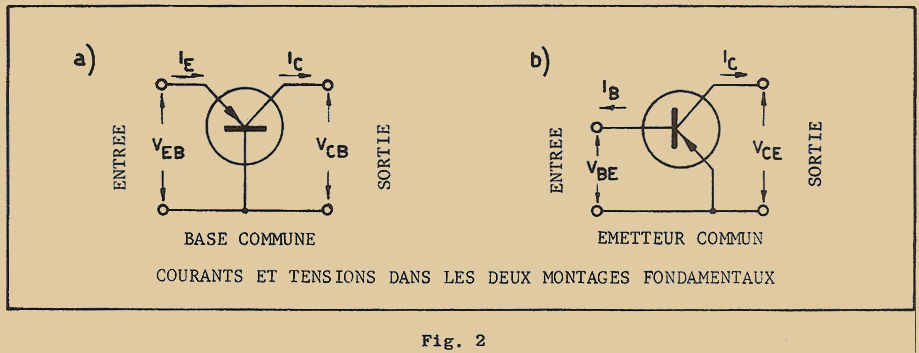
1 – 1 CARACTÉRISTIQUES CORRESPONDANT AU MONTAGE EN BASE COMMUNE

Pour relever les courbes caractéristiques d’un transistor donné, il est nécessaire de disposer de quatre appareils qui ont à mesurer les quatre grandeurs considérées et de deux générateurs de courant continu (en général des piles) dont les tensions et les courants doivent être réglables dans la limite des valeurs pour lesquelles le transistor à essayer a été construit.

Pour relever les caractéristiques correspondant au montage en base commune, le schéma à réaliser est celui indiqué à la figure 3. Comme vous pouvez le voir, il y a une pile A qui sert à polariser dans le sens direct la jonction émetteur-base, le courant de commande de l’émetteur peut être réglé et ajusté à l’aide du rhéostat R_A et mesuré par le milliampèremètre M₁. Le millivoltmètre V₁ mesure la tension entre émetteur et base. De cette manière, V₁ indique la tension d’entrée qui dans ce cas est la tension émetteur-base V_EB, M₁ indique le courant d’entrée, c’est-à-dire le courant d’émetteur I_E.

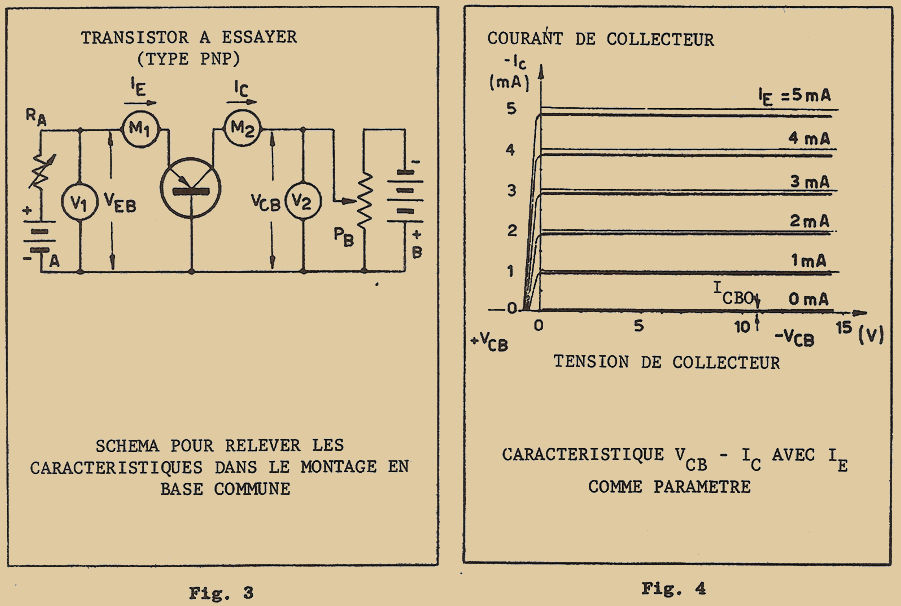
On procède de la même façon, pour polariser la jonction collecteur-base en sens inverse, à l’aide de la pile B. Les grandeurs de sortie peuvent être réglées et ajustées à l’aide du potentiomètre P_B ; leurs valeurs sont mesurées par les appareils V₂ et M₂ qui indiquent respectivement la tension de sortie (tension collecteur-base) et le courant de sortie (courant de collecteur).

Si l’on désire tracer par exemple, la famille de courbes caractéristiques de sortie avec le courant d’entrée comme paramètre (c’est-à-dire la famille V_CB – I_C avec I_E comme paramètre) qui est la plus importante car la plus utile pour établir le projet d’un circuit, on devra procéder comme suit :

On coupe la liaison de l’émetteur, de façon à rendre nul le courant à l’entrée (I_E = 0) et en agissant sur le potentiomètre P_B on règle la tension de collecteur aux valeurs suivantes : 0V, 1V, 2V, 3V, 4V, etc …jusqu’à atteindre la valeur maximum désirée. En correspondance avec ces valeurs, lues sur V₂, on lit les valeurs du courant de collecteur sur M₂.

Il est facile de prévoir les résultats, car ayant interrompu la liaison de l’émetteur, le transistor se comporte comme une simple diode, formée par la jonction collecteur-base, polarisée en sens inverse.

La courbe que l’on obtient en reportant sur un graphique les valeurs de la tension et du courant trouvées n’est autre que la caractéristique inverse d’une diode. On aura ainsi construit la première courbe de la famille qui sera représentée par I_E = 0 pour rappeler qu’elle a été déterminée en maintenant le courant de l’émetteur à la valeur zéro (figure 4).

Comme nous l’avons vu dans la leçon précédente, pour une tension de collecteur nulle, le courant du collecteur est nul aussi, et la courbe passe donc par l’origine 0 des axes du graphique. Si l’on augmente la tension du collecteur le courant prend rapidement une valeur qui reste ensuite pratiquement constante (et très faible) correspondant au courant résiduel du transistor appelé I_CBo. Etant donné la faible valeur de ce courant, la courbe I_E = 0 se confond pratiquement avec l’axe horizontal.

Pour tracer les autres courbes, on rebranche la connexion de l’émetteur et on règle le rhéostat R_A, jusqu’à lire sur M₁, une valeur donnée du courant de l’émetteur, par exemple 1mA. Dans ces conditions, on va de nouveau faire varier la tension du collecteur de volt en volt et noter les valeurs correspondantes du courant de collecteur lu sur M₂.

Comme dans le montage en base commune, le courant de collecteur a une valeur inférieure, mais peu différente du courant émetteur, on lira sur M₂ un courant peu différent de 1mA et cette valeur restera pratiquement constante non seulement lorsque l’on augmentera la tension du collecteur, mais encore lorsque la tension sera nulle. Ceci est dû au fait, comme on l’a vu en son temps, que même si l’on n’applique pas de tension sur le collecteur, la barrière de potentiel de la jonction collecteur-base est suffisante pour recueillir sur le collecteur presque tous les porteurs émis par l’émetteur.

En reportant sur le graphique de la figure 4, les paires de valeurs obtenues pour la tension et le courant du collecteur, on obtient la caractéristique indiquée par I_E = 1mA. Celle-ci est pratiquement rectiligne et se situe un peu au-dessous de la ligne indiquée par 1mA et tracée en traits fins. On obtient ainsi avec une bonne approximation I_C = α I_E où α est un peu inférieur à 1.

Si on veut annuler le courant de collecteur, il ne suffit plus d’annuler la tension du collecteur comme dans le cas où l’on avait I_E = 0, mais encore il faut inverser la tension V_CB de façon à annuler l’effet de la barrière de potentiel et à empêcher les porteurs émis par l’émetteur d’atteindre le collecteur.

Dans le cas d’un transistor PNP, il faudra polariser le collecteur par une tension positive : on obtient ainsi la partie de la caractéristique tracée à gauche de l’axe vertical de la figure 4 où l’on peut voir comment le courant du collecteur chute rapidement à zéro dès que la tension positive du collecteur atteint une valeur de 0,5 V environ.

Pour tracer d’autres courbes de cette famille, il suffira de procéder de la même manière, en réglant successivement le courant de l’émetteur à 2mA, 3mA, 4mA, etc … jusqu’à la valeur maximum admissible pour le type du transistor essayé.

A la figure 4, on a représenté un exemple de famille de courbes caractéristiques V_CB – I_C. Etant donné que l’on considère un transistor PNP, il faut, pour obtenir la polarisation inverse de la jonction collecteur-base, que la tension de collecteur soit négative ; de cette façon, la tension collecteur-base est indiquée sur le graphique en portant le signe "moins" et on doit écrire - V_CB ; de la même manière le courant de collecteur est indiqué par - I_C.

Une telle famille de courbes caractéristiques se présente comme formée par autant de lignes presque horizontales par rapport aux tensions négatives du collecteur (courbes à droite de l’axe vertical) et rapidement descendantes pour des tensions positives (courbes à gauche de l’axe vertical).

Une autre famille de courbes caractéristiques très importante pour établir un projet de circuit à transistors est celle de l’entrée en prenant la tension de collecteur comme paramètre.

Pour tracer ces courbes, on utilise encore le schéma de la figure 3. Il suffit d’amener la tension du collecteur à une valeur déterminée en agissant sur le potentiomètre P_B et de faire varier le courant de l’émetteur de zéro jusqu’à la valeur maximum admissible, en agissant sur R_A.

Pour chaque valeur de I_E lue sur M₁, on note la valeur correspondante de V_EB indiquée par V₁. En reportant ces couples de valeurs sur un graphique on obtient une courbe caractéristique.

Les autres caractéristiques s’obtiennent de façon analogue, en maintenant la tension de collecteur à des valeurs différentes.

A la figure 5, je vous ai reporté comme exemple une famille de cinq courbes caractéristiques V_EB – I_E, ayant pour paramètre, les valeurs de tension de collecteur de 0V, 1V, 5V, 10V, et 15V. Ces courbes sont relatives au même type de transistor PNP dont nous avons tracé les caractéristiques à la figure 4.

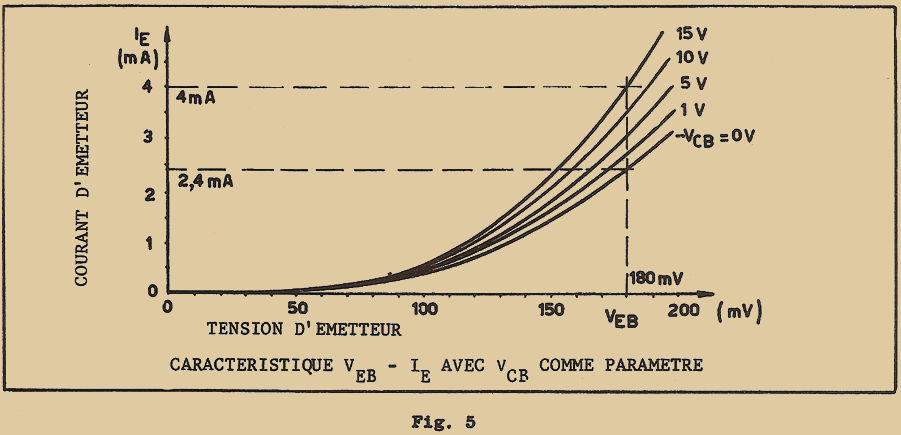
Comme ces caractéristiques sont celles de la jonction émetteur-base, polarisée en sens direct, il est logique de penser qu’elles auront l’allure de la caractéristique directe d’une diode à jonction.

La tension que l’on applique au collecteur a pour effet de rendre cette diode d’autant plus conductrice qu’elle est plus élevée. Il suffit en effet de remarquer à la figure 5 que pour une tension de 180 mV appliquée entre l’émetteur et la base, le courant de l’émetteur est de 2,4mA pour une tension nulle de collecteur, et de 4mA pour une tension de collecteur de 15V.

Maintenant que vous avez vu comment on pouvait déterminer les deux caractéristiques principales, il est facile de comprendre, comment on peut déterminer, n’importe quelle autre caractéristique. Il suffit en effet de régler convenablement R_A et P_B de la figure 3, et lire les valeurs des grandeurs qui nous intéressent, pour construire, point par point, la courbe désirée, comme par exemple la caractéristique mutuelle des courants avec comme paramètre la tension de collecteur (figure 6).

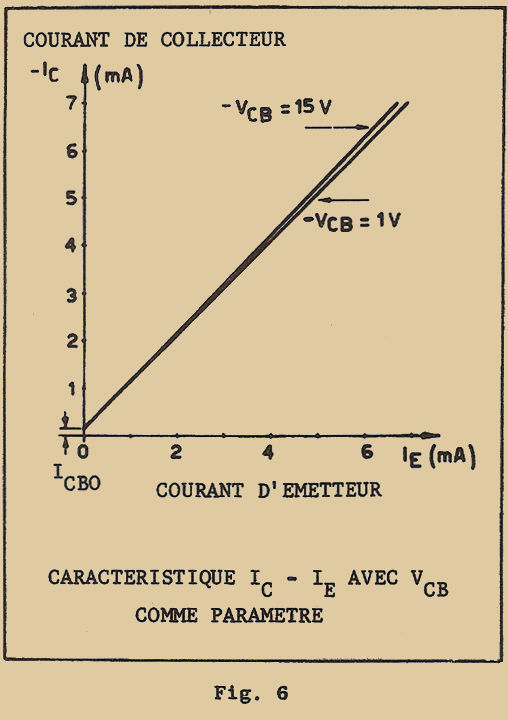
Cette dernière est obtenue en maintenant constante la tension du collecteur, et en mesurant les valeurs du courant de collecteur en fonction des différentes valeurs du courant de l’émetteur.

Comme vous pouvez le voir sur la figure de telles courbes caractéristiques sont presque "les unes sur les autres" : pour plus de clarté, je ne vous ai dessiné que deux seulement, correspondant à des tensions de collecteur de 1 V et de 15 V. Les caractéristiques intermédiaires seraient tracées entre ces deux courbes.

L’explication de ceci provient du fait que le courant de collecteur est très peu influencé par la tension de collecteur : en faisant varier celle-ci, la caractéristique varie très peu.

Il encore remarquer que les caractéristiques considérées sont pratiquement rectilignes, car il y a une assez bonne proportionnalité entre courant de collecteur et courant d’émetteur.

Notez encore, que les différentes caractéristiques ne passent pas par l’origine des axes, mais coupent l’axe vertical au point correspondant au courant résiduel de collecteur I_CBo : en effet pour I_E = 0, le courant de collecteur ne s’annule pas complètement, mais conserve une faible valeur.

1 – 2 COURBES CARATÉRISTIQUES EN MONTAGE ÉMETTEUR COMMUN

Pour relever les courbes caractéristiques relatives au montage en émetteur commun, il suffit de modifier le schéma de la figure 3 comme indiqué à la figure 7. Remarquez encore, que M₁ est maintenant un microampèremètre car le courant de base est très faible. Si l’on prend à nouveau un transistor PNP les polarisations sont encore négatives et les valeurs des tensions et des courants sont précédées par convention par le signe moins. Nous aurons donc la tension et le courant de base (grandeurs d’entrée) indiqués respectivement par – V_BE et – I_B, la tension et le courant de collecteur (grandeurs de sortie) par – V_CE et – I_C.

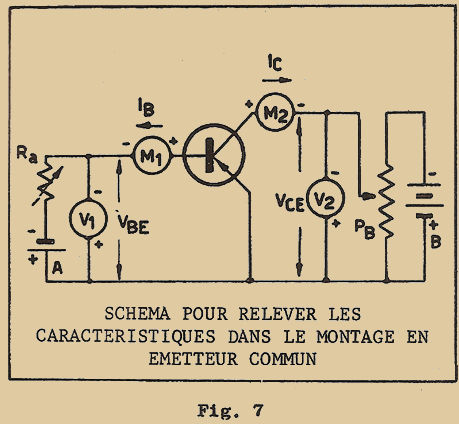
Etant donné que les opérations à suivre pour relever ces caractéristiques sont celles qui ont déjà été décrites pour le montage en base commune il suffit simplement de vous les indiquer et de les commenter.

Les courbes caractéristiques de sortie ayant pour paramètre le courant de base (courant de commande), se présentent comme sur la figure 8. Comme différence essentielle par rapport aux courbes analogues de la figure 4, celles-ci ne sont plus maintenant parallèles, mais d’autant plus inclinées que le courant de base est plus élevé. Ceci est dû au fait que maintenant la tension du collecteur a une certaine influence sur le courant I_C et qu’ainsi en l’augmentant on accroît I_C.

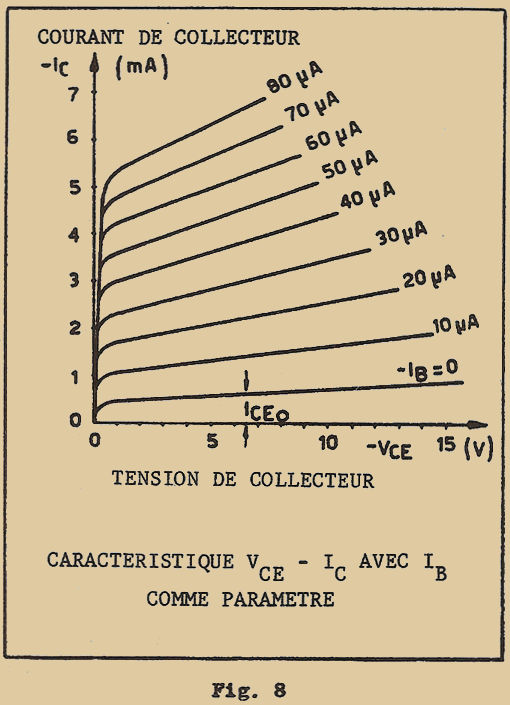
Autre fait à noter : avec le montage en émetteur commun, le courant de collecteur s’annule lorsque l’on annule la tension V_CE. Ainsi, toutes les caractéristiques partent de l’origine 0 des axes. En augmentant la tension de collecteur, le courant I_C croît d’abord rapidement pour atteindre une certaine valeur (qui dépend du courant que l’on fait circuler dans la base), puis il continue à croître, mais beaucoup plus lentement.

Chaque caractéristique est donc composée de deux parties bien distinctes : une partie presque verticale qui correspond à des valeurs très faibles de la tension de collecteur, l’autre presque horizontale, pour des valeurs plus grandes de V_CE.

Les deux parties presque rectilignes sont raccordées par une partie courbe que l’on appelle Coude de la caractéristique.

Dans la dernière partie presque verticale, le courant de base a peu d’influence sur la valeur de I_C qui ne dépend presque que de la tension de collecteur. C’est pour cette raison que la partie verticale est presque commune à toutes les caractéristiques qui viennent se raccorder à celle-ci, comme on peut le voir sur la figure 8.

Il faut noter encore, que la caractéristique correspondant à un courant de base nul (– I_B = 0) est obtenue en supprimant la liaison de la base : elle n’est plus confondue avec l’axe horizontal comme sur la figure 4, mais elle en est bien distincte. En effet, sa distance à l’axe représente le courant résiduel du collecteur I_CEo, qui comme nous l’avons vu dans une leçon précédente est beaucoup plus grand que I_CBo qui correspond lui au montage en base commune.

Si l’on trace maintenant les caractéristiques d’entrée avec la tension de collecteur comme paramètre, celles-ci se présentent comme sur la figure 9. Vous remarquerez qu’elles sont encore semblables à celles de la figure 5 correspondantes en base commune, puisqu’elles représentent toujours la caractéristique de la diode formée par la jonction base-émetteur, polarisée en sens direct. Tandis que dans le cas de la figure 5, les différentes caractéristiques partaient de la valeur zéro de la tension de base, dans le cas de la figure 9 elles partent à partir de la valeur 100mV environ. Ceci signifie que pour un courant de base nul (liaison de base "en l’air") il apparait entre la base et l’émetteur une faible partie de la tension appliquée entre le collecteur et l’émetteur, comme nous l’avons vu dans la précédente leçon. Vous noterez encore, que la tension de la base passe de 100mV à 110mV environ lorsque la tension de collecteur passe de 1V à 15V.

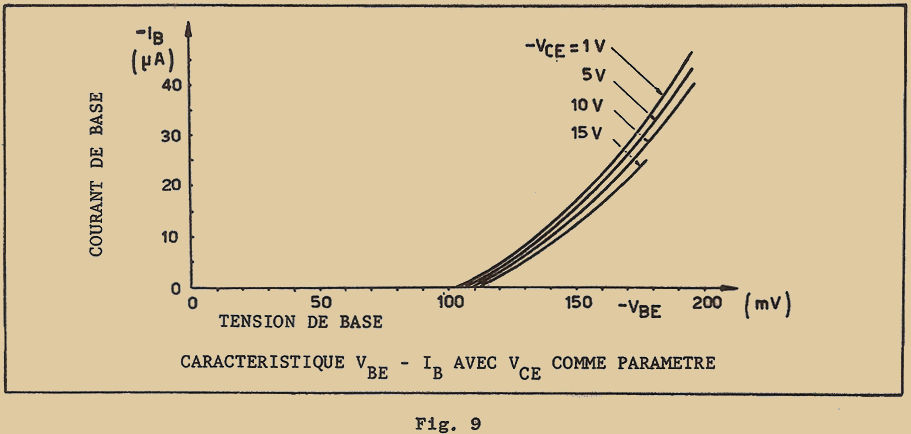
Enfin, pour les courbes caractéristiques mutuelles de courants avec comme paramètre, la tension de collecteur (figure 10), les considérations faites à propos de la figure 6 restent encore valables. Nous remarquerons seulement que maintenant les différentes caractéristiques sont beaucoup plus éloignées les unes des autres car la tension du collecteur a une certaine influence sur la valeur du courant I_C.

Chacune des courbes caractéristiques coupe l’axe vertical à une distance de l’origine 0, égale à la valeur du courant résiduel I_CEo qui correspond à la valeur de la tension de collecteur que cette courbe a comme paramètre.

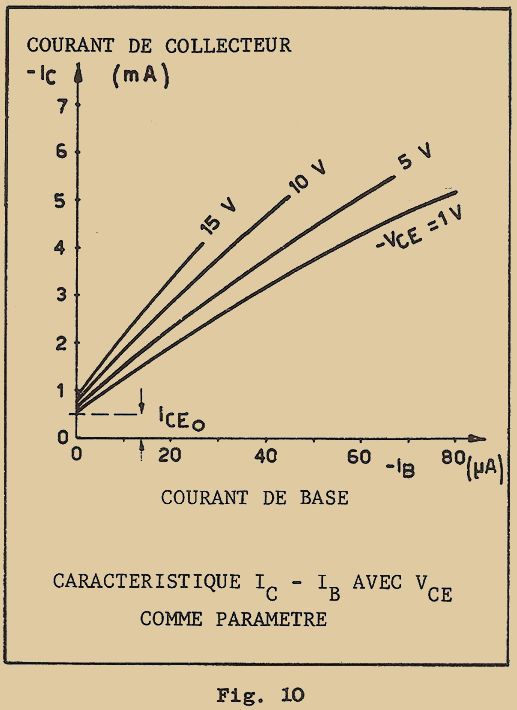
Les trois familles de courbes caractéristiques que nous avons illustrées dans les cas de montage en base commune ou en émetteur commun, sont les plus commodes pour établir des projets d’étapes amplificateurs.

Elles sont relatives à des transistors à jonction PNP utilisés comme préamplificateurs de basse fréquence.

Les courbes relatives à des transistors pour d’autres usages mais toujours de faible puissance, ne diffèrent pas sensiblement de celles que nous avons étudiées. Pour les transistors de puissance, en basse fréquence, elles se différencient par des valeurs de courants de collecteur (qui peuvent atteindre des dizaines ou des centaines de milliampères ou même pendant quelques instants quelques ampères), et des courants de base (de l’ordre du milliampère, ou même d’une dizaine de milliampères, au lieu de microampères).

On peut aussi étudier les transistors NPN, de la même façon la grande différence résidant dans les symboles des tensions et des courants : ceux-ci ne sont plus précédés du signe – dans le cas du montage en émetteur commun, tandis que dans le cas du montage en base commune, ce signe moins précède les symboles relatifs au circuit d’entrée (émetteur) au lieu que ce soit pour le circuit de sortie (collecteur).

2 – UTILISATION PRATIQUE DES COURBES CARACTÉRISTIQUES

Maintenant que nous avons vu comment nous pouvions relever les courbes caractéristiques, il est intéressant de savoir comment nous devons les utiliser pour connaître les conditions de fonctionnement du transistor dans un circuit déterminé, et inversement, comment nous devons monter un transistor pour qu’il travaille dans des conditions établies à l’avance.

Pour résoudre de tels problèmes, nous nous serviront surtout des caractéristiques de sortie V_C – I_C qui ont comme paramètre le courant de commande (I_E pour le montage en base commune, et I_B pour le montage en émetteur commun) et que l’on appelle encore souvent Caractéristiques de collecteur. Leur utilisation est subordonnée à la notion du point de fonctionnement et à celle de la droite de charge. Nous allons illustrer ces notions en prenant le cas d’un transistor PNP monté en émetteur commun, ce que l’on rencontre le plus souvent en pratique. Ce que nous allons dire maintenant restera valable aussi dans le cas du montage en base commune (il suffira uniquement de considérer les caractéristiques correspondantes à ce montage), de même évidemment pour les transistors du type NPN.

2 – 1 POINT DE FONCTIONNEMENT

Je prends donc le cas d’un transistor PNP monté en émetteur commun (voir figure 2-b). Si l’on applique une certaine tension entre le collecteur et l’émetteur et si l’on fait traverser la base par un certain courant de commande, on déterminera un courant de collecteur bien défini. Le transistor fonctionnera donc dans des conditions particulières, définies par la valeur de la tension du collecteur, de la valeur du courant de base et de celle du courant de collecteur ; cette condition particulière de fonctionnement est représentée par un point bien défini sur la caractéristique.

Ainsi, le point A de la caractéristique de la figure 11 représente les conditions particulières de fonctionnement caractérisées par les valeurs suivantes :

• tension de collecteur V_CE = 5 V lue sur l’échelle horizontale en correspondance de la ligne verticale tracée à partir du point A.
• courant de collecteur I_C = 4mA lue sur l’échelle verticale en correspondance de la ligne horizontale tracée à partir du point A.
• courant de base I_B = 70µA : c’est la valeur du paramètre de la caractéristique qui passe par le point A

Pour déterminer sur la caractéristique, le point de fonctionnement, il suffit de connaître deux des trois valeurs indiquées ; en en connaissant deux, on retrouve facilement la troisième. On peut alors résoudre les trois problèmes suivants :

1. Etant donné une certaine tension V_CE appliquée au collecteur, déterminer le courant I_B qui doit traverser la connexion de base pour obtenir un certain courant de collecteur I_C.
2. Etant donnée une certaine tension V_CE appliquée au collecteur, déterminer le courant du collecteur I_C que l’on obtient pour un courant de base I_B donné.
3. Etant donné un certain courant de base I_B, déterminer la tension du collecteur V_CE pour obtenir un courant de collecteur I_C demandé.

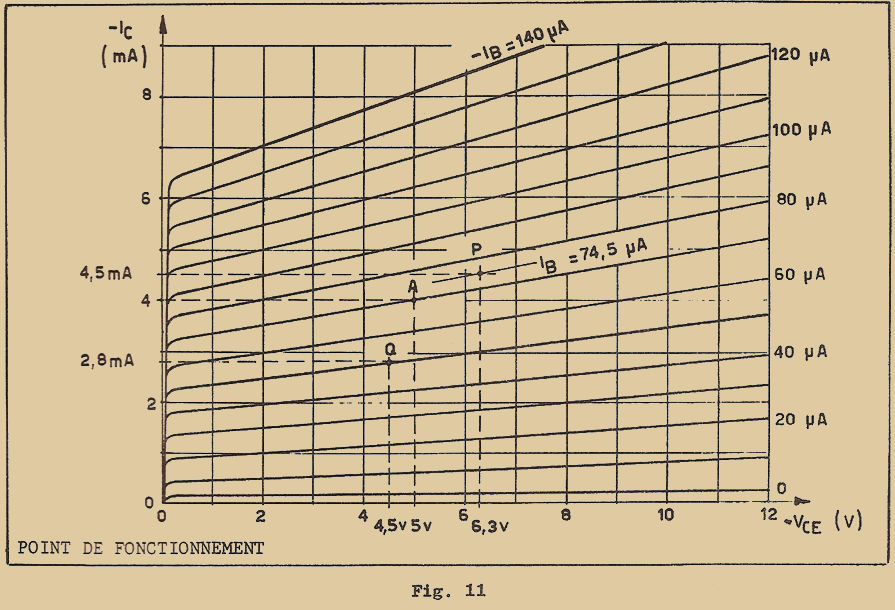
Prenons quelques exemples :

Problème N° 1 - On désire alimenter le transistor à l’aide d’une tension de 6,3 V (V_CE = 6,3 V) et on voudrait obtenir un courant de collecteur de 4,5mA (I_E = 4,5mA). Quel est le courant de base I_B nécessaire  ?

Il faut en premier lieu déterminer sur la caractéristique, le point de fonctionnement défini par les valeurs V_CE = 6,3 V et I_C = 4,5mA. Un tel point est obtenu par l’intersection de la verticale menée par le point de l’axe horizontal correspondant à la valeur de tension de 6,3 V et de l’horizontale menée à partir du point de l’axe vertical correspondant à la valeur du courant de 4,5mA (point P de la figure 11).

Si le point de fonctionnement se trouve sur une caractéristique, la valeur du courant de base est donnée directement par cette courbe. Lorsqu’au contraire, le point de fonctionnement tombe entre deux caractéristiques comme c’est le cas sur la figure (entre les caractéristiques 70µA et 80µA) La valeur du courant I_B sera comprise entre les valeurs des paramètres correspondant (c’est-à-dire entre 70µA et 80µA).

La valeur exacte de I_B est déterminée par interpolation entre les deux courbes. Ceci se pratique comme indiqué sur la figure 12 où l’on a agrandi la partie de la figure 11 autour du point P.

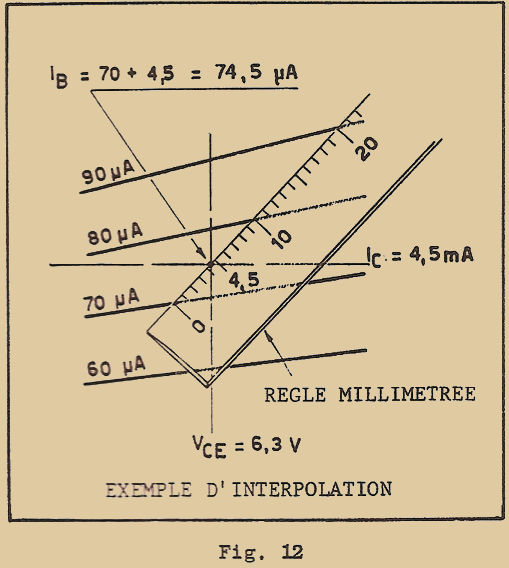
On prend une règle millimétrée et on l’incline de façon à faire coïncider le zéro de la graduation avec la caractéristique 70µA et la graduation 10 mm avec la caractéristique 80µA en prenant soin de faire passer l’arête de la règle par le point P.

La valeur lue sur la règle millimétrée ajoutée à la valeur du bas donne la valeur du courant de base cherchée.

Ainsi, dans notre exemple, en face du point P, nous lisons sur la règle 4,5 mm : la valeur de I_B sera donc 70 + 4,5 = 74,5µA.

Problème N°2 – On se fixe une tension de collecteur V_CE = 4,5 V et on désire connaître la valeur du courant de collecteur que l’on obtient pour un courant de base de I_B = 50µA.

Le point de fonctionnement Q (figure 11) est déterminé par l’intersection de la verticale menée à partir de l’axe horizontal, au point correspondant à la valeur de 4,5 V avec la caractéristique de paramètre I_B = 50µA. En traçant par le point Q une droite horizontale jusqu’à l’intersection avec l’axe vertical, on obtient sur celui-ci, la valeur du courant cherché : I_C = 2,8mA.

Si la valeur de I_B ne correspond pas à une courbe caractéristique on doit interpoler entre les deux caractéristiques les plus voisines en utilisant la méthode décrite sur la figure 12.

Le troisième problème est moins fréquent en pratique ; je ne vous donnerai donc pas d’exemple numérique. Mais il est facile de comprendre comment il faut le résoudre.

2 – 2 DROITE DE CHARGE

Nous allons encore nous borner au transistor PNP monté en émetteur commun, mais en intercalant cette fois dans son circuit de collecteur une résistance, comme indiqué sur la figure 13. Cette résistance est appelée Résistance de charge ou Résistance de collecteur, elle est indiquée par R_C. Nous voulons savoir maintenant comment se déplace le point de fonctionnement du transistor monté de cette façon.

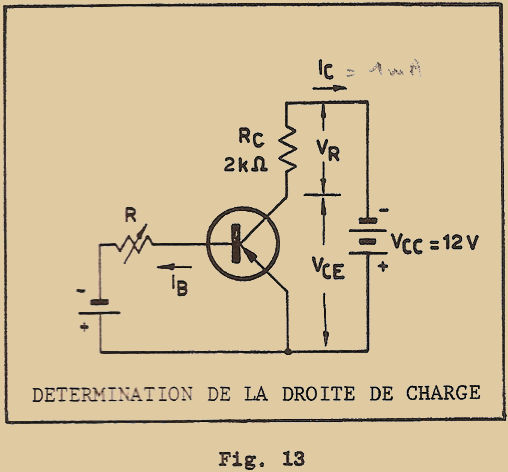
Supposons que la tension d’alimentation du collecteur V_CC soit de 12 V et que la résistance de charge soit de 2 kΩ. Nous voyons tout de suite que la tension V_CE effectivement appliquée entre le collecteur et l’émetteur n’est pas égale à la tension d’alimentation, mais qu’elle est plus faible, puisqu’une certaine chute de tension a lieu dans la résistance R_C dûe au courant I_C.

Ainsi par exemple si l’on règle le courant de collecteur à la valeur de 1mA, en agissant sur le rhéostat R la chute de tension V_R aux bornes de R_C sera donnée par la loi d’Ohm : 1mA x 2 kΩ = 2 V. La tension V_CE ne sera donc pas de 12 V, mais seulement de 12 – 2 = 10 V.

Si le courant de collecteur augmente : 2mA, 3mA, 4mA, 5mA, la chute de tension aux bornes de R_C augmentera et deviendra 4V, 6V, 8V, 10V ; la tension entre collecteur et émetteur descendra à 8V, 6V, 4V, 2V.

Si l’on porte ces différents points de fonctionnement sur les caractéristiques de la figure 14 (points numérotés de 1 à 5), on remarque que ces points sont parfaitement alignés et qu’il est possible de les réunir par une ligne droite. Cette droite est appelée droite de charge.

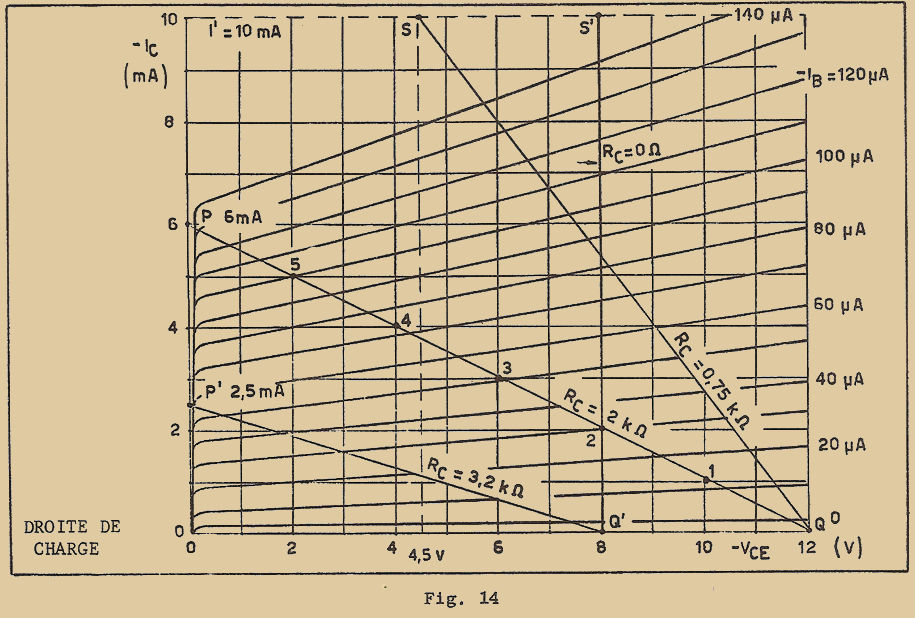
Il est intéressant de remarquer qu’en prolongeant la droite de charge au-delà des points 1 et 5, celle-ci coupe l’axe horizontal au point correspondant à la tension d’alimentation (12 V dans le cas de notre exemple) et l’axe vertical au point correspondant à la valeur du courant obtenu en divisant la tension d’alimentation par la résistance de charge.

Ainsi, dans notre exemple, la droite de charge rencontre l’axe vertical au point correspondant à 12 V / 2 kΩ = 6mA qui est précisément la valeur du courant qui traverserait la résistance R_C si celle-ci était reliée directement aux bornes de la pile d’alimentation du collecteur.

Etant donné que pour tracer la droite de charge il suffit d’en connaître deux points, il est beaucoup plus commode en pratique de déterminer ces deux points particuliers (indiqués sur la figure 14 par les lettres P et Q) qui se trouvent à l’intersection avec les axes vertical et horizontal.

La position de la droite de charge dépend uniquement de la valeur de la tension d’alimentation qui définit le point Q, et de la valeur de la résistance de charge qui, avec la tension d’alimentation, définit le point P selon la relation que nous avons vue ci-dessus.

Par exemple, si la tension d’alimentation V_CC est de 8 V et la résistance de charge de 3,2 kΩ, la droite de charge sera tracée en joignant les points Q’ et P’ obtenus respectivement sur l’axe horizontal au point 8 V et sur l’axe vertical au point 8 V/3,2 kΩ = 2,5mA (figure 14).

Il peut arriver quelquefois que le point P se trouve en dehors du graphique et ne puisse être déterminé sur l’axe vertical. Prenons par exemple : V_CC = 12 V et R_C = 750 Ω (= 0,75 kΩ).

Dans ce cas, le point sur l’axe horizontal correspond encore au point Q déjà vu, tandis que le point sur l’axe vertical correspond à la valeur 12 V / 0,75 kΩ = 16mA qui n’est pas portée sur le graphique.

La droite de charge pourra alors être tracée en considérant le point S que l’on peut obtenir sur la ligne horizontale passant par la valeur maximum I’ du graphique (I’ = 10mA dans notre exemple).

Le point S (figure 14) se trouve sur la verticale passant par la valeur V’ lue sur l’axe horizontal et donnée par la formule :

V’ = V_CC – I’ R_C

Dans le cas de notre exemple, nous aurons :

V’ = 12 -10 x 0,75 = 12 – 7,5 = 4,5 V (figure 14)

Il faut remarquer encore que la droite de charge est d’autant moins inclinée sur l’axe horizontal, que la valeur de R_C est plus petite : elle devient même verticale, quand la résistance de charge est nulle, ce qui signifie que le collecteur est branché directement sur la pile (R_C = 0 Ω).

En effet, si R_C = 0 Ω et que V_CC = 8 V, le point S’ se trouvera sur la verticale passant par la valeur V’ = 8 – 10 x 0 = 8 – 0 = 8 V, c’est-à-dire précisément sur la verticale passant par le point Q’ : la droite de charge est donc verticale.

Les problèmes qui peuvent être résolus à l’aide des droites de charge seront illustrés par quelques exemples dans la prochaine leçon.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 8^ème LEÇON THÉORIQUE

1 – Dans le montage en base commune, la base est reliée à la masse et le courant de collecteur est commandé par le courant d’émetteur ; au contraire, dans le montage en émetteur commun, le courant de collecteur est commandé par le courant de base et l’émetteur est relié à la masse

2 – Dans le montage en émetteur commun, une faible fraction de la tension de polarisation du collecteur polarise dans le sens direct la jonction émetteur-base et provoque une émission de porteurs de l’émetteur même ; c’est pour cette raison que le courant I_CEo est plus grand que le courant I_CBo.

3 – Le coefficient d’amplification de courant β est donné par la valeur du courant de collecteur, diminué du courant résiduel, et divisé par la valeur du courant de base.

4 – Les valeurs courantes du coefficient d’amplification de courant β sont comprises entre 20 et 200 environ.

5 – Le montage en émetteur commun présente l’avantage par rapport à celui en base commune, d’un gain de courant plus grand et d’un gain de puissance supérieur. Par contre l’inconvénient principal est le courant résiduel plus grand.

6 – Dans le symbole graphique d’un transistor l’émetteur est repéré par une flèche qui indique le sens de conduction de la jonction émetteur-base.

7 – Le symbole graphique d’un transistor PNP se distingue de celui d’un transistor NPN par le sens de la flèche de l’émetteur : dans le premier cas la flèche est tournée vers l’intérieur, dans le second vers l’extérieur.

8 – La tension du collecteur a une polarité positive dans le cas des transistors NPN et négative dans les transistors PNP.

9 – La polarité de la tension appliquée à l’électrode de commande d’un transistor est la même que celle appliquée au collecteur dans le cas du montage en émetteur commun, et inverse dans le cas du montage en base commune.

---

EXERCICES DE RÉVISION SUR LA 9^ème LEÇON THÉORIQUE

1 – Qu’appelle-t-on famille de courbes caractéristiques de sortie  ?

2 – Quelle est la famille de courbes caractéristiques la plus importante pour un transistor en montage en base commune  ?

3 – Comment se présentent les courbes caractéristiques V_CB – I_C avec comme paramètre I_E, c’est-à-dire celles qui correspondent au montage en base commune  ?

4 – Pourquoi les caractéristiques mutuelles de courant ayant comme paramètre V_CB (relatives au montage en base commune) sont-elles pratiquement superposées l’une à l’autre  ?

5 – Quelles sont les différences essentielles dans la forme des caractéristiques de sortie (ayant comme paramètre, le courant d’entrée) correspondant aux montages en base commune et à l’émetteur commun  ?

6 – Qu’appelle-t-on point de fonctionnement d’un transistor  ?

7 – A quelle résistance donne-t-on le nom de résistance de charge  ?

8 – Qu’appelle-t-on droite de charge  ?

9 – De quoi dépend l’inclinaison de la droite de charge  ?

Fin de la leçon 9

---

LECON 10

1 – CIRCUITS DE POLARISATION

Dans la leçon précédente, nous avons défini ce que l’on appelle "le point de fonctionnement" d’un transistor et comment on pouvait tracer la droite de charge sur les caractéristiques.

Aujourd’hui, nous nous proposons d’étudier la façon de polariser un transistor.

Les circuits de polarisation les plus simples sont indiqués aux figures 1-a et 1-b dans les cas respectifs de montage en base commune, et montage en émetteur commun. Vous pouvez constater dès à présent que dans le premier cas, deux piles distinctes sont nécessaires, étant donné que l’émetteur et le collecteur nécessitent des tensions de polarité opposée ; dans le second cas au contraire, la base et le collecteur nécessitent des tensions de même polarité, et une seule pile est utilisée.

Ceci est un autre avantage du montage en émetteur commun par rapport à celui de la base à la masse.

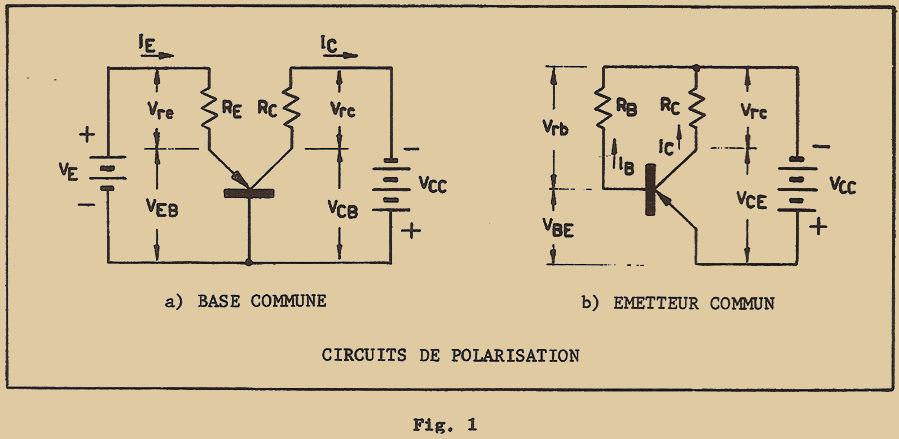
Les schémas de la figure 1 correspondent à des transistors du type PNP ; si l’on voulait utiliser un transistor NPN, il suffirait d’inverser la polarité des piles.

1 – 1 MONTAGE EN BASE COMMUNE

Le circuit de polarisation indiqué à la figure 1-a, est constitué par deux résistances, une de charge de collecteur R_C, l’autre de polarisation de l’émetteur R_E. La détermination des valeurs de ces résistances ne peut être faite qu’après avoir fixé la valeur des tensions des deux piles et choisi le point de fonctionnement du transistor.

Supposons un transistor PNP que nous désirons faire travailler avec un courant de collecteur de 2mA et une tension de collecteur de 5 V. La pile de polarisation délivre une tension négative V_CC de 9 V et celle de polarisation de l’émetteur une tension positive V_E de 3 V.

Pour déterminer rapidement les valeurs de R_C et R_E, il suffit de faire deux approximations qui en pratique sont tout à fait acceptables : on admettra que le courant de collecteur I_C et celui de l’émetteur I_E sont égaux (ce qui en pratique est presque vrai, puisque α est très peu différent de 1 et que I_CBo est pratiquement négligeable par rapport à I_C). On peut admettre encore que la tension V_EB est négligeable devant la tension V_E de la pile (en effet, V_E est de l’ordre de quelques volts, tandis que V_EB est compris entre 0,1 et 0,2 V environ).

Avec ces simplifications, les valeurs des deux résistances peuvent être calculées facilement à l’aide des deux formules suivantes :

R_C = (V_CC - V_CB)/I_C et R_E= (V_E )/I_E = (V_E )/I_C

Les valeurs des résistances seront exprimées en kΩ, si les tensions le sont en volts et les courants en mA. Nous trouvons donc :

R_C = (9 - 5)/2 = 2kΩ R_E = 3/2 = 1,5 kΩ

Un cas différent du précédent, mais très intéressant, est la détermination du point de fonctionnement d’un transistor d’un circuit donné, déjà réalisé. On veut donc déterminer les valeurs du courant de collecteur I_C et de la tension collecteur-base V_CB quand on connait les valeurs des deux résistances ainsi que la tension des piles de polarisation. Un tel problème peut être utile dans le cas où l’on désire essayer un transistor dans les conditions de fonctionnement indiquées sur un schéma. On peut encore faire les mêmes approximations que ci-dessus :

I_C = I_E = (V_E )/R_E V_CB = V_CC – R_C I_C

Les unités de mesure restent les mêmes.

Prenons un exemple numérique : V_CC = 9 V et V_E = 3 V. Nous avons R_E = 1,2 kΩ et R_C = 1,8 kΩ ; nous obtenons :

I_C = I_E = 3/1,2 = 2,5mA ; V_CB = 9 – 2,5 x 1,8 = 9 – 4,5 = 4,5 V

Si l’on désire effectuer un calcul plus précis, il faut tenir compte de la tension V_EB et du coefficient α du transistor. Le calcul est alors :

I_C = α I_E = α (V_E - V_EB)/R_E

tandis que la tension collecteur-base est déterminée par la formule précédente.

EXEMPLE : α = 0,955 et V_EB = 0,15 V environ : les valeurs calculées précédemment sont modifiées et deviennent :

I_C = 0,955 x (3 - 0,15)/1,2 = 0,955 x 2,85/1,2 = 0,955 x 2,37 = 2,27mA

V_CB = 9 – 2,27 x 1,8 = 9 – 4,08 = 4,92 V

Comme vous le voyez, la différence n’est pas très grande et dans la pratique courante, on peut utiliser les formules simplifiées.

1 – 2 MONTAGE EN EMETTEUR COMMUN

Le schéma utilisé est celui de la figure 1-b ; une seule pile suffit à polariser le collecteur et la base. Pour déterminer les valeurs des résistances de collecteur R_C et de base R_B il est indispensable de connaître le point de fonctionnement, la tension de la pile et la valeur du coefficient d’amplification du courant β, sinon, il faut avoir recours aux courbes caractéristiques relatives au montage en émetteur commun.

Comme la polarisation de la base est obtenue par la même tension d’alimentation que celle du collecteur qui est toujours de quelques volts (en général de 4,5 V à 12 V ou plus), on peut encore, et pour une raison encore plus évidente que dans le cas précédent, négliger dans les calculs la tension base-émetteur V_BE qui reste de l’ordre de un ou deux dixièmes de volt.

Si l’on ne dispose pas de courbes caractéristiques de collecteur, le calcul des valeurs des résistances de collecteur et de base peut être fait très simplement si l’on néglige le courant résiduel I_CEo par rapport au courant I_C de fonctionnement. Ceci peut être admis avec une approximation suffisante, si la valeur de I_C est environ cinq fois plus grande que celle du courant résiduel I_CEo. Pour les transistors courants qui ne sont pas de puissance, le courant résiduel I_CEo peut être négligé lorsque I_C est supérieur à 1mA. Prenons un exemple numérique. Supposons un transistor du type PNP utilisé comme préamplificateur BF avec un β = 48. Nous voulons que le point de fonctionnement soit défini par les valeurs : I_C = 3mA ; V_CE = 4,5 V. La tension d’alimentation V_CC est de 9 V.

On obtient :

R_C = (V_CC - V_CE)/I_C = (9 - 4,5)/3 = 4,5/3 = 1,5 kΩ

La valeur obtenue n’est exacte qu’en fonction des approximations faites, la chute de tension Vrc aux bornes de la résistance, est la différence entre la tension d’alimentation et la tension que l’on désire avoir sur le collecteur.

Par contre le calcul de la valeur de R_B est beaucoup plus approximatif car on commet une première erreur dans le calcul de I_B (puisque l’on néglige I_CEo) et une seconde en négligeant la tension V_BE.

La valeur de I_B est obtenue facilement en divisant I_C par β. Dans notre exemple, nous obtenons :

I_B = I_C/β = 3/48 = 0,0625mA

D’où :

R_B = V_CC/I_B = 9/0,0625 = 144 kΩ

Si l’on doit par contre déterminer le point de fonctionnement dans un certain circuit, on commence par calculer le courant de base, puis celui de collecteur et enfin la tension du collecteur. Ainsi par exemple si l’on a R_B = 120 kΩ, R_C = 1,5 kΩ, une tension d’alimentation de 9 V et un β de 48, on obtient :

I_B = V_CC/R_B = 9 / 120 = 0,075mA = 75µA

I_C = β x I_B = 48 x 75 = 3.600µA = 3,6mA

V_CE = V_CC – R_C x I_C = 9 – 1,5 x 3,6 = 9 – 5,4 = 3,6 V

Le calcul est encore approximatif, non seulement parce que l’on a négligé la tension base-émetteur V_BE et le courant résiduel I_CEo, mais aussi parce que la valeur de β, varie d’un point de fonctionnement à l’autre (comme nous le verrons plus tard) : ainsi ne connaissant pas à priori le point de fonctionnement, on ne connait pas la valeur vraie de β (dans l’exemple précédent, la valeur de β = 48 n’est valable que pour I_C = 3mA et V_CE = 4,5 V).

Le calcul est cependant suffisant dans la plupart des cas, pour effectuer des mesures de contrôle sur le circuit étudié.

1 – 3 UTILISATION DES COURBES CARACTÉRISTIQUES DE COLLECTEUR

Pour faire un calcul plus exact des valeurs des résistances de la base et du collecteur ou bien pour déterminer avec une précision plus grande, le point de fonctionnement d’un transistor monté dans un circuit donné, il faut faire appel aux courbes caractéristiques de collecteur ainsi qu’à celles de V_BE en fonction de V_CE. Comme en général, la tension V_BE peut être négligée, les caractéristiques de collecteur seules suffiront (figure 2).

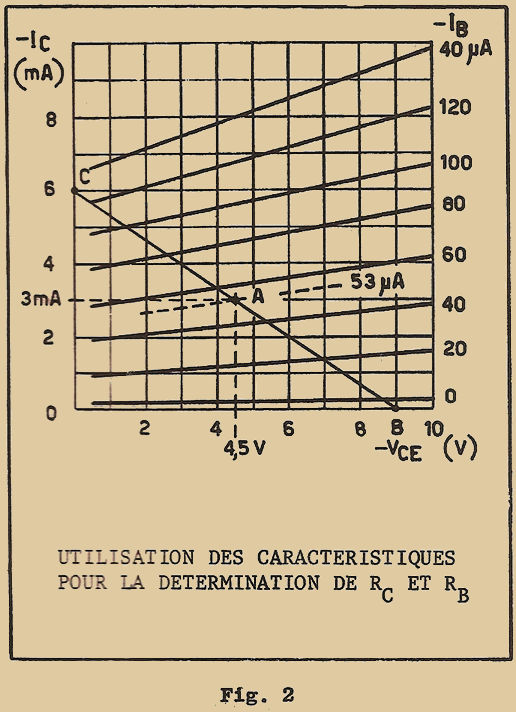
Les courbes caractéristiques de la figure 2 sont relatives au transistor type SFT 352. Les signes "moins" placés devant les symboles des tensions et des courants, servent à indiquer, comme je vous l’ai déjà dit, que ces grandeurs sont négatives, car on considère un transistor du type PNP.

Supposons que l’on désire faire fonctionner le transistor au point de fonctionnement déjà considéré dans l’exemple du calcul précédent (tension de collecteur V_CE = 4,5 V, courant de collecteur I_C = 3mA et alimentation par une tension de 9 V). Ce point de fonctionnement sera représenté sur la caractéristique du collecteur par le point A.

Pour déterminer la valeur de la résistance R_C, on doit tracer la droite de charge ; celle-ci doit passer nécessairement par le point de fonctionnement (point A de la figure 2) et par le point B qui représente sur l’axe horizontal la tension d’alimentation V_CC. Il suffit de joindre ces deux points par une droite qui, prolongée, coupe l’axe vertical au point C.

La valeur de R_C est donnée par le rapport entre la tension d’alimentation (valeur lue au point B) et le courant lu sur l’axe vertical en face du point C.

Dans notre cas le courant est de 6mA.

D’où :

R_C = 9/6 = 1,5 kΩ

Cette valeur est la même que celle trouvée précédemment puisque dans le calcul de R_C, n’intervient ni β, ni I_CEo, il est donc indifférent d’utiliser la formule ou d’opérer sur les courbes.

Par contre, dans la détermination de la valeur de R_B, on obtient une valeur plus correcte en utilisant les courbes, car on tient automatiquement compte de la valeur exacte de β au point de fonctionnement ainsi que de la valeur de I_CEo ce que l’on avait négligé dans les précédents calculs.

Le processus du calcul de R_B est donc le suivant. On détermine en premier lieu, la valeur de I_B correspondant à la caractéristique qui passe par le point de fonctionnement. Dans le cas de l’exemple le point A tombe entre deux caractéristiques. Il faut donc interpoler sa valeur, comme je vous l’ai indiqué dans la leçon précédente. On trouve pour I_B la valeur de 53µA.

La valeur de R_B est alors immédiatement donnée par :

R_B = V_CC/I_B = 9/53 = 0,17 MΩ = 170 kΩ

En comparant cette valeur à celle que l’on avait obtenue précédemment on peut se faire une idée sur la différence qui résulte des deux méthodes de calcul. On trouve maintenant un courant de 53µA au lieu de 62,5µA, et une résistance de base de 170 kΩ au lieu de 144 kΩ. Ces différences sont dûes au fait que l’on a négligé dans le premier cas le courant résiduel de collecteur I_CEo ; elles sont toutefois faibles et restent tolérables pour de nombreux calculs pratiques.

Dans la détermination du courant I_B, il est presque toujours nécessaire de faire une interpolation car il est rare que le point de fonctionnement tombe exactement sur une courbe. Comme cette opération risque d’être assez imprécise, on l’évite et on a recours à la caractéristique mutuelle de courant (que le constructeur donne en général avec les courbes de collecteur, ou que l’on détermine soi-même comme indiqué plus loin). Le calcul de I_B est alors fait comme indiqué sur la figure 3. A droite de l’axe vertical sont reportées les courbes caractéristiques de collecteur de la figure 2, sur lesquelles on a tracé la droite de charge correspondant à R_C = 1,5 kΩ, droite qui passe par le point de fonctionnement A. A gauche du même axe, on a dessiné la caractéristique mutuelle I_C – I_B avec comme paramètre la valeur de la tension de collecteur relative au point de fonctionnement que l’on désire obtenir : 4,5 V.

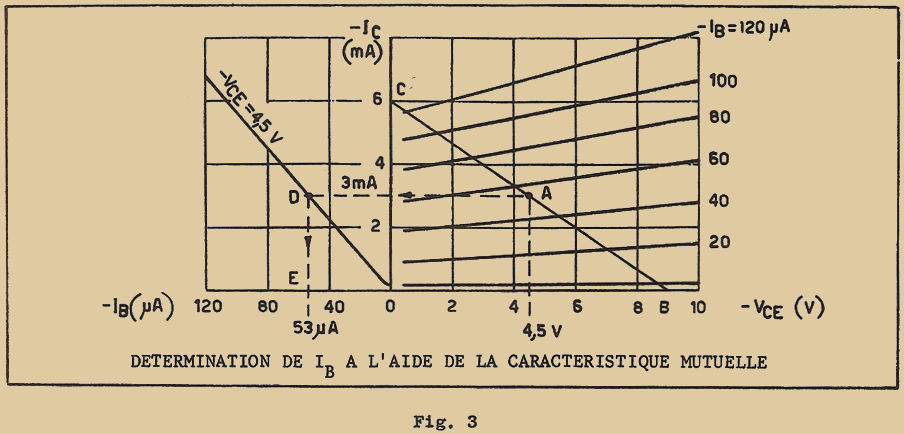
La détermination du courant de base se fait alors très simplement en traçant la droite horizontale passant par le point A (trait en pointillés de la figure 3) jusqu’à l’intersection avec la caractéristique mutuelle (point D) et en abaissant la verticale jusqu’à rencontrer l’axe horizontal.

En face du point E on lit la valeur du courant de base : 53µA comme on l’avait trouvé précédemment d’ailleurs par interpolation (figure 2).

Si l’on ne dispose pas de caractéristique mutuelles ou si la caractéristique mutuelle qui nous intéresse n’existe pas (on trouve assez souvent dans les données techniques des fabricants la caractéristique relative à la tension V_CE de 4,5 V), celle-ci peut-être dessinée de la façon suivante en partant des courbes de collecteur.

Supposons que le point de fonctionnement du transistor corresponde à une tension de collecteur V_CE = 7,5 V et que l’on désire avoir la caractéristique mutuelle correspondant à cette tension.

On cherchera sur l’axe horizontal de la caractéristique de collecteur (figure 4) la valeur de 7,5 V et on tracera à partir de ce point, une droite verticale. Celle-ci va rencontrer les différentes caractéristiques aux points marqués A, B, C, D, E, F, G, H, correspondants respectivement aux courbes qui ont comme paramètre les valeurs suivantes du courant de base : 0, 20, 40, 60, 80, 100, 120, 140µA

On tracera ensuite, à partir de l’origine 0, un axe horizontal vers la gauche que l’on divisera en des intervalles égaux et correspondant aux valeurs du courant de base trouvées ci-dessus.

On déterminera ainsi le point A’ comme étant l’intersection de l’horizontale menée par le point A (courbe de paramètre 0µA) et de la verticale menée par le point de l’échelle horizontale de gauche correspondant au même courant 0µA. On déterminera ensuite de la même façon, le point B’ (paramètre 20µA) puis les points C’, D’, E’, F’, G’ et H’. En joignant tous ces points, on obtiendra la caractéristique mutuelle relative à la tension de 7,5 V de collecteur.

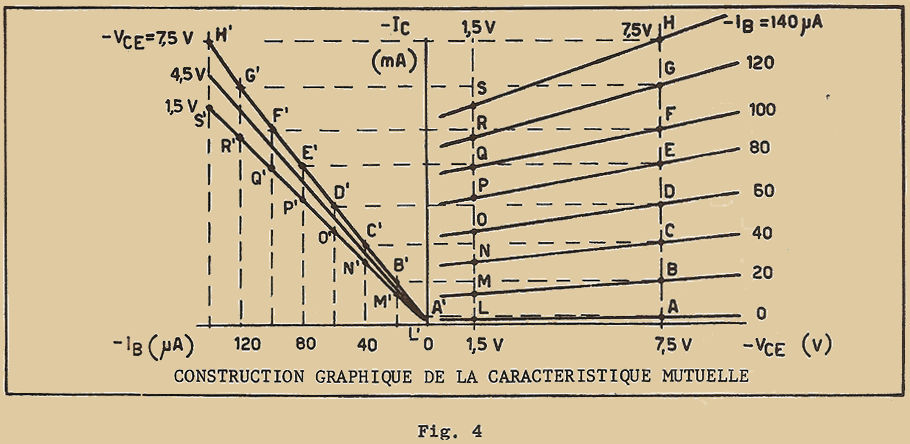
A titre d’exemple, je vous ai dessiné sur la même figure la caractéristique mutuelle relative à une tension V_CE de 1,5 V. D’autre part, la courbe correspondante à V_CE = 4,5 V (la même que celle de la figure 3) a été représentée pour montrer la variation de telles courbes en fonction de la tension du collecteur, ce qui permet ainsi d’évaluer l’erreur commise en n’utilisant pas la courbe correcte.

Il reste encore à voir comment déterminer à l’aide des courbes caractéristiques le point de fonctionnement d’un transistor lorsque ce dernier est polarisé à l’aide des résistances de collecteur et de base de valeurs données.

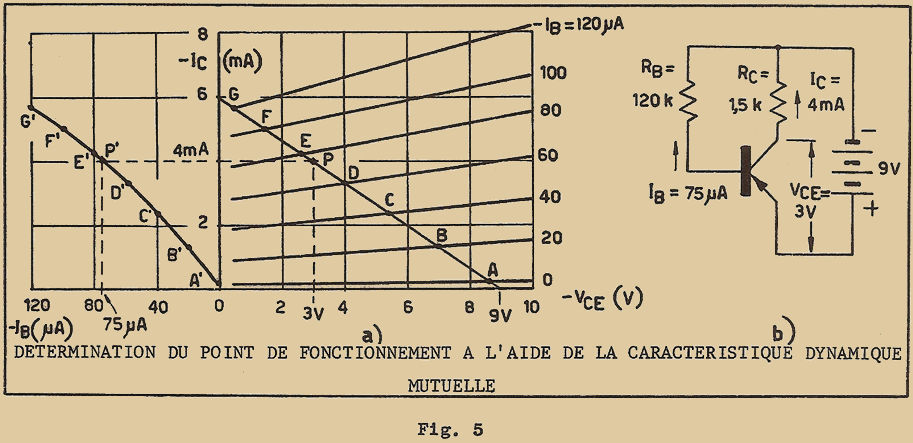
EXEMPLE : Transistor SFT 352 alimenté par une tension V_CC = 9 V et polarisé par des résistances R_B = 120 kΩ et R_C = 1,5 kΩ.

Il faut tout d’abord tracer sur les caractéristiques de collecteur, la droite de charge relative à la valeur R_C = 1,5 kΩ, droite qui passe par le point correspondant à 9 V sur l’axe horizontal et par le point 9 V / 1,5 kΩ = 6mA de l’axe vertical (figure 5-a). On calcule ensuite la valeur du courant de base qui est égal à 9 V / 120 kΩ = 75µA si l’on néglige encore la tension V_BE. Le point de fonctionnement est déterminé par l’intersection de la droite de charge avec la caractéristique qui a comme paramètre, un courant de base de 75µA. Comme une telle caractéristique n’est pas dessinée, il faudra encore une fois interpoler comme déjà indiqué, entre les caractéristiques 60µA et 80µA (point de fonctionnement P). D’où la valeur du courant est I_C = 4mA et la tension : V_CE = 3 V.

Une détermination plus exacte du point P s’obtiendrait en utilisant la caractéristique mutuelle. Il faut remarquer toutefois que ne connaissant pas encore la tension du collecteur V_CE, on ne sait pas à priori quelle caractéristique mutuelle on doit prendre. On peut tourner l’obstacle, en utilisant une caractéristique mutuelle particulière, appelée Caractéristique Dynamique qui a l’avantage de pouvoir être obtenue non pas pour une tension de collecteur déterminée mais pour la droite de charge utilisée ; c’est sur cette caractéristique que se déplace nécessairement le point de fonctionnement.

Pour tracer la caractéristique mutuelle dynamique, pour une droite de charge R_C = 1,5 kΩ (figure 5-a) on procèdera de la même façon que sur la figure 4, sauf que maintenant, les points A, B, C etc sont déterminés par l’intersection de cette droite de charge avec les différentes courbes caractéristiques de collecteur au lieu que ce soit avec la droite verticale passant par une valeur déterminée de V_CE.

On obtient la caractéristique dynamique en joignant les points A’, B’, C’, etc … On trace ensuite la verticale par le point 75µA (lu sur l’axe horizontal de gauche) jusqu’à rencontrer la courbe au point P’, puis une horizontale passant par P’, jusqu’à obtenir l’intersection avec la droite de charge, ce qui fixe le point de fonctionnement P.

En regardant la figure 5-a, on voit que l’on retrouve les valeurs I_C = 4mA et V_CE = 3 V. Cette méthode donne une précision bien meilleure, mais elle est par contre moins rapide. De même dans la détermination du point de fonctionnement, l’utilisation des caractéristiques donne des résultats plus précis.

2 – VALEURS LIMITES

De tout ce qui vient d’être dit, on pourrait penser que le point de fonctionnement d’un transistor peut être placé comme on le veut et où on le veut. En réalité, il faut remarquer que chaque transistor présente des limites bien définies qui dépendent de son type, de ses dimensions et de sa constitution. Il est évident par exemple, qu’un transistor de faibles dimensions ne peut fournir la même puissance qu’un transistor de grandes dimensions. Pour chaque type de transistor, le constructeur donne des valeurs limites qui ne doivent en aucun cas être dépassées dans les conditions normales de fonctionnement pour éviter de le détruire irrémédiablement, ou plus simplement, pour éviter qu’il ne fonctionne dans de mauvaises conditions.

• Les limites que donne en général le fabricant, sont les suivantes :
• courant maximum de collecteur I_C max
• tension maximum de collecteur V_CE max
• puissance maximum de collecteur P_C max
• température maximum de la jonction Tj max

D’autres valeurs limites peuvent aussi être fournies, comme celles qui intéressent la base et l’émetteur.

Ainsi par exemple, pour un transistor BF de faible puissance le fabricant donne comme indiqué ci-dessus les valeurs limites absolues pour une température ambiante de 25°C.

• tension collecteur-émetteur V_CE max = - 30 V
• tension émetteur-base V_EB = - 12 V
• courant collecteur I_C max = - 10mA
• dissipation à l’air libre P_C max = 75mW
• température de la jonction Tj max = 75°C

Ces valeurs ne doivent jamais être dépassées dans un fonctionnement normal du transistor, c’est-à-dire que l’on peut choisir le point de fonctionnement arbitrairement, mais il faudra veiller à ce qu’aucune des valeurs ci-dessus ne soit jamais dépassée (courant, tension, puissance).

2 – 1 VALEUR MAXIMUM DU COURANT DE COLLECTEUR

La valeur maximum du courant de collecteur qui peut être admise dans un transistor donné est imposée par deux considérations différentes.

La première considération est de caractère "de conservation" en ce qui concerne la vie du transistor. On sait qu’un conducteur quelconque est détruit s’il est parcouru par un courant trop intense par rapport à sa section transversale. Dans le cas d’un transistor, la limite est imposée par la section de la jonction collecteur-base, car celle-ci est traversée par l’ensemble du courant de collecteur. Plus cette section sera grande, plus le courant qui la traverse pourra être élevé, sans risque de destruction et sans altération des caractéristiques du transistor.

A section égale de la jonction, la valeur maximum du courant pourra être différente selon les impuretés introduites et selon le type de semi-conducteur utilisé.

Une autre considération différente concerne le fonctionnement correct du transistor ; en effet, le coefficient d’amplification diminue lorsque le courant de collecteur croît et prend des valeurs très faibles par rapport à celles qu’il a lors d’un fonctionnement normal.

Si donc le transistor doit travailler avec un coefficient d’amplification trop faible, on trouve une nouvelle limite au courant de collecteur.

Les deux limites ainsi définies ne sont évidemment pas les mêmes, et il faut choisir la plus restrictive.

A la figure 6, je vous ai dessiné les courbes caractéristiques d’un transistor de faible puissance BF. Une ligne horizontale passe par le point de l’échelle verticale correspondant à I_C max = 10mA (valeur maximum admise pour ce type de transistor).

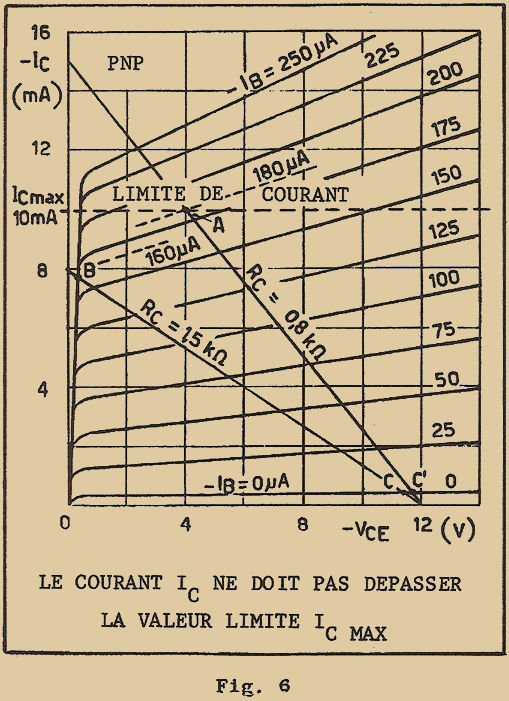
Le point de fonctionnement devra être choisi de telle façon qu’il soit toujours en dessous de cette ligne et jamais au-dessus. Si le transistor travaille avec une résistance de charge R_C en série avec le collecteur on peut considérer deux cas différents, suivant que la droite de charge coupe ou non la droite horizontale correspondant à la limite du courant de collecteur.

Supposons par exemple qu’on alimente le transistor avec une tension V_CC = 12 V par l’intermédiaire d’une résistance de charge de 0,8 kΩ. La droite de charge passe par le point 12 V de l’axe horizontal et par le point 12 V / 0,8 kΩ = 15mA de l’axe vertical. Elle coupe donc la droite horizontale de limite de courant au point A de la figure 6.

Le point de fonctionnement qui, comme nous l’avons vu, se déplace obligatoirement sur la droite de charge, ne devra en aucune façon dépasser le point A. Ceci signifie que le courant de polarisation de la base pourra au maximum prendre la valeur correspondant à celle de la caractéristique passant par le point A, c’est-à-dire 180µA.

Dans ce cas, une fois que l’on a défini la valeur de la résistance de charge, la limitation de courant de collecteur dépend de la limitation du courant de base.

Augmentons maintenant la résistance de charge et amenons-la à 1,5 kΩ (la droite de charge passant toujours par le point 12 V de l’axe horizontal). Elle rencontre l’axe vertical au point 12 V / 1,5 kΩ = 8mA. Elle ne coupe plus la droite horizontale limite.

Dans ce dernier cas, si l’on augmente graduellement le courant de base, le point de fonctionnement se déplace jusqu’en B, lorsque I_B prend la valeur de 160µA environ. Si l’on continue à augmenter encore le courant de base, le point de fonctionnement ne peut aller au-delà du point B car les caractéristiques qui correspondent aux valeurs de I_B supérieures à 160µA, rencontrent toutes la droite de charge donnée au même point B. On dit alors que le courant de collecteur a atteint sa valeur de saturation.

Quand la droite de charge ne rencontre pas la ligne horizontale limite du courant maximum de collecteur, on n’a pas besoin de s’inquiéter de la valeur de I_C max, qui restera toujours inférieure à la limite.

Si l’on diminue par contre le courant de base, le point de fonctionnement se déplace vers le bas, et atteint au maximum le point C, lorsque I_B se réduit à zéro.

On peut donc en conclure que :

1. quand la droite de charge coupe la droite horizontale limite du courant collecteur, le point de fonctionnement ne doit jamais dépasser le point A (figure 6) et par ailleurs il ne peut descendre en dessous de C’.
2. Quand la droite de charge ne rencontre pas la droite I_C max, les seules limites sont le point B (vers le haut) et le point C (vers le bas).

2 – 2 VALEUR MAXIMUM DE LA TENSION DE COLLECTEUR

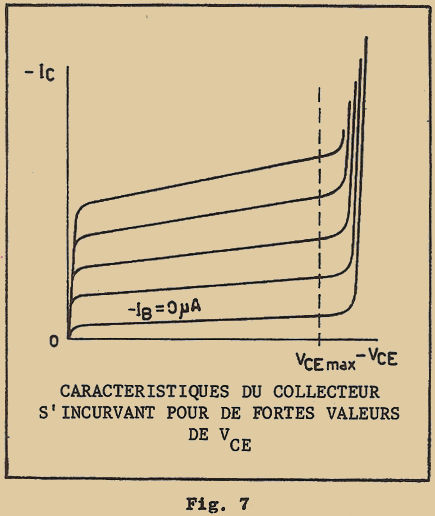
Lorsque nous avons étudié la diode à jonction, nous avons vu qu’un phénomène dit de Zener apparaissait dès que la tension inverse appliquée à la jonction dépassait une certaine valeur. Le même phénomène apparait dans les transistors, puisque la jonction collecteur-base se comporte de la même façon qu’une diode polarisée en inverse.

Lorsque nous relevons les courbes caractéristiques de collecteur, si nous continuons à augmenter la tension de collecteur, nous observons qu’à un moment donné, le courant I_C commence à augmenter très rapidement, et la courbe s’incurve vers le haut (figure 7).

On observe d’ailleurs le même phénomène lors du montage en base commune. Dans les deux cas il ne faut pas dépasser la valeur maximum de la tension appliquée au collecteur si l’on ne veut pas faire fonctionner le transistor dans cette partie incurvée de la courbe, ce qui risquerait, ou bien de le détruire irrémédiablement, (on a d’ailleurs vu qu’une diode normale ne devait pas travailler non plus dans la zone de Zener), ou bien de le faire travailler dans de mauvaises conditions.

Dans le cas de la diode polarisée en inverse, l’augmentation du courant était dûe exclusivement à l’effet Zener (ou à l’effet d’avalanche) ; dans le transistor un tel phénomène peut être dû à une autre cause (figure 8).

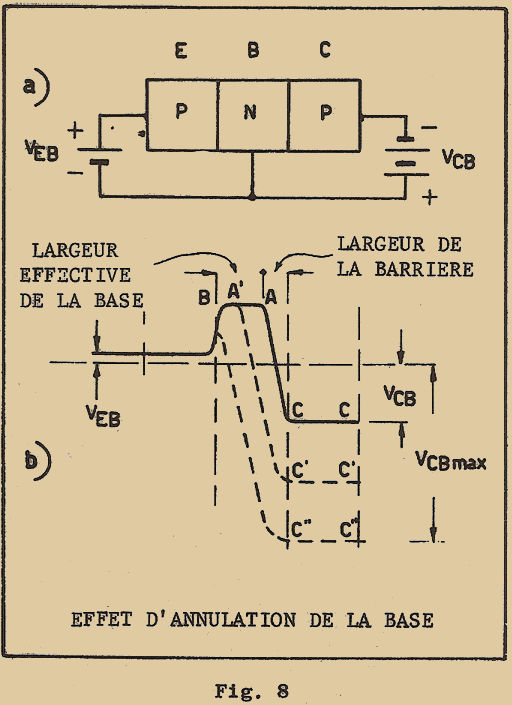
En effet, si l’on regarde le graphique des barrières de potentiel qui s’établissent aux jonctions d’un transistor lorsque celui-ci est polarisé comme sur la figure 8-a, on peut remarquer que la barrière relative à la jonction collecteur-base (ligne AC - figure 8-b) se situe presque exclusivement dans la base, car celle-ci est moins dopée que le collecteur.

Pour cette raison, la largeur réelle de la base n’est pas celle de la zone du semi-conducteur du type N qui constitue la base, mais seulement une fraction de celle-ci, et précisément la largeur BA indiquée sur la figure 8-b. Si l’on augmente la tension appliquée entre le collecteur et la base, la droite CC se déplace vers le bas, par exemple en C’C’. Par conséquent, le point A se déplace en A’ et réduit encore davantage la largeur de la base. On voit tout de suite, que si la tension de collecteur augmente encore, la droite CC continuera à descendre de plus en plus, et le point A continuera à se déplacer vers la gauche en réduisant la largeur réelle de la base.

A un moment donné, quand la droite CC s’est déplacé en C’’C’’, la largeur de la base est complétement annulée et on ne peut plus vérifier "l’effet transistor".

Le transistor se comporte alors comme un bloc unique de germanium P (en effet dans le montage en base commune, ou entre le collecteur et l’émetteur dans le montage en émetteur commun, est ainsi déterminé par les trois phénomènes : effet Zener, effet d’avalanche, effet d’annulation de la base).

Suivant le type du transistor, la tension maximum du collecteur peut varier de 10 V à 40 V environ ; seuls quelques transistors au silicium peuvent supporter des tensions de l’ordre d’une centaine de volts.

Sur les caractéristiques de collecteur (figure 7), la tension maximum V_CE max délimite vers la droite une zone interdite. Le point de fonctionnement doit se trouver à gauche de cette valeur V_CE max.

2 – 3 VALEUR MAXIMUM DE LA PUISSANCE DE DISSIPATION DU COLLECTEUR

Le point de fonctionnement est caractérisé par une valeur de la tension V_CE et par un courant I_C. Les deux valeurs expriment donc : la tension appliquée entre le collecteur et l’émetteur, le courant absorbé par le transistor ; le produit de ces deux valeurs n’est autre que la puissance fournie au transistor par le circuit d’alimentation du collecteur.

P_C = V_CE x I_C

Elle sera exprimée enmW, si la tension est donnée en volts et le courant en mA. Comme cela arrive pour n’importe quelle résistance, le transistor s’échauffe quand il est parcouru par un courant (effet Joule).

Par suite d’un tel échauffement, la température interne du transistor, ou plus précisément la température de la jonction collecteur-base, augmente et devient plus grande que la température ambiante dans laquelle se trouve plongé le transistor. L’augmentation de la température de la jonction sera d’autant plus élevée que la puissance P_C dissipée au collecteur sera plus grande. On comprend donc qu’il y aura une certaine limite à fixer à P_C pour que la température de la jonction soit maintenue entre certaines limites non dangereuses pour le transistor.

L’augmentation de la température de la jonction peut être calculée par la simple formule suivante :

T’j = K x P_C

où T’j indique l’augmentation de la température en °C, P_C la puissance dissipée au collecteur enmW et K un coefficient appelé "résistance thermique" du transistor. La valeur de K est exprimée en °C/mW et dépend du type de transistor : elle indique de combien de degrés augmente la température de la jonction pour chaque milliwatt de puissance dissipée sur le collecteur. Ainsi, par exemple si pour un certain transistor on a K = 0,4°C/mW et s’il travaille sous une tension V_CE = 5 V avec un courant I_C = 3mA, la puissance P_C sera 5 V x 3mA = 15mW ; l’augmentation de la température de sa jonction sera de 0,4 x 15 = 6°C.

La température Tj à laquelle est portée la jonction sera alors donnée simplement par la somme de la température Ta de l’ambiance dans laquelle est plongé le transistor et de l’augmentation T’j de la température de la jonction dûe à P_C ; on a donc :

Tj = Ta + T’j

Dans l’exemple précédent, si la température de l’ambiante est de 25°C, la température de la jonction sera 25 + 6 = 31°C. Si au contraire, la température de l’ambiante est de 50°C, on aura Tj = 50 + 6 = 56°C. Il peut sembler étrange de parler d’une température ambiante de 50°C, mais il faut tenir compte de la température ambiante dans laquelle est plongé le transistor, et de ce que cette ambiante peut être élevée à cause de l’échauffement dû aux résistances et aux transistors de puissance qui se trouvent dans le voisinage immédiat du transistor considéré. Afin que le transistor ne soit pas endommagé, il faut veiller à ce que la température de la jonction ne dépasse pas la température limite, en général de l’ordre de 75 °C pour les transistors au germanium et 150°C pour ceux au silicium.

Comme la température de la jonction dépend non seulement de l’augmentation de température due à la puissance P_C, mais aussi de la température ambiante, on en déduit que la puissance maximum P_C max admissible du collecteur (pour un type de transistor donné) ne doit pas dépasser une certaine valeur.

Pour cette raison le constructeur indique toujours la valeur P_C max pour une température ambiante donnée. Il donne par exemple P_C max = 75mW pour Ta = 45°C.

Si on donne les valeurs de K et de Tj max (c’est-à-dire les valeurs de la résistance thermique et de la température maximum admise pour la jonction), on peut calculer la valeur de P_C max en fonction de la température ambiante qui nous intéresse, par la formule suivante :

P_C max = (T_j max - T_a)/K

Soit par exemple : Tj max = 75°C K = 0,4°C/mW

On trouve la puissance maximum que l’on peut dissiper sur le collecteur à une température ambiante de 35°C :

P_C max (à 35°C) = (75-35)/0,4 = 40/0,4 = 100mW

Le fabricant donne quelquefois un graphique où sont reportées les valeurs de P_C max en fonction de la température ambiante (de 25°C à 75°C pour les transistors au germanium, de 25°C à 150°C dans le cas des transistors au silicium) (figure 9). Comme vous pouvez le voir, la puissance maximum dissipable sur le collecteur diminue rapidement lorsque la température ambiante croît, jusqu’à s’annuler pour T_a égale à la température maximum admissible par la jonction.

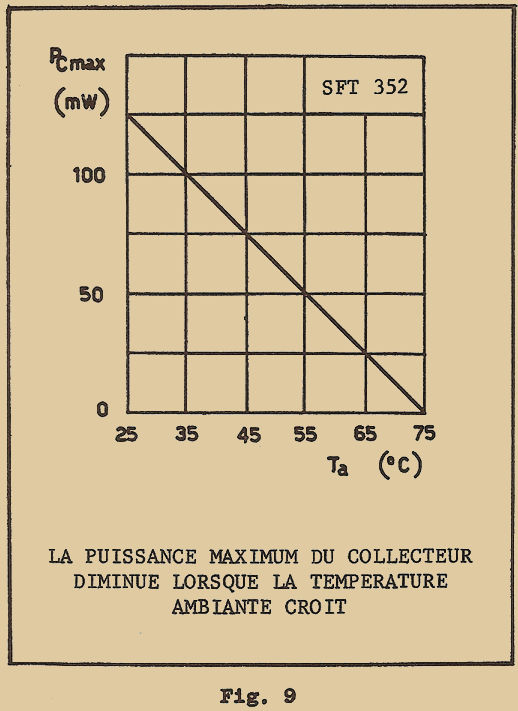
En effet, si la température de l’ambiante est de 75°C, la jonction est aussi portée à cette température et ne peut donc admettre aucune augmentation de température.

Dans ces conditions, le transistor ne peut plus dissiper aucune puissance. P_C aussi faible que possible provoquerait une augmentation de la température de la jonction et celle-ci dépasserait 75°C.

Nous allons voir maintenant comment la limitation de P_C max peut être figurée sur les caractéristiques du collecteur.

En se rappelant que la puissance de collecteur P_C est donnée par le produit de la tension V_CE par le courant I_C, on voit que l’on peut avoir sur les courbes caractéristiques autant de points de fonctionnement que l’on désire, pour lesquels P_C prend cette valeur.

Ces points sont en effet déterminés par les paires de valeurs V_CE et I_C qui multipliées entre elles donnent P_C. Si on prend par exemple P_C = 20mW on trouve les paires de valeurs suivantes :

POINT DE FONCTIONNEMENT	VCE	IC	PC = VCE x TC
A	10V	2mA	10 x 2 = 20mW
B	8V	2,5mA	8 x 2,5 = 20mW
C	5V	4mA	5 x 4 = 20mW
D	4V	5mA	4 x 5 = 20mW
E	2,5V	8mA	2,5 x 5 = 20mW
F	2V	10mA	2 x 10 = 20mW

En reportant ces différents points sur les courbes caractéristiques (figure 10) et en les joignant par une ligne on obtient une courbe dite à puissance constante, puisque pour tous les points de cette courbe, la puissance dissipée sur le collecteur est toujours la même : 20mW. De façon analogue on peut tracer d’autres courbes à puissance constante, correspondant à d’autres valeurs de P_C.

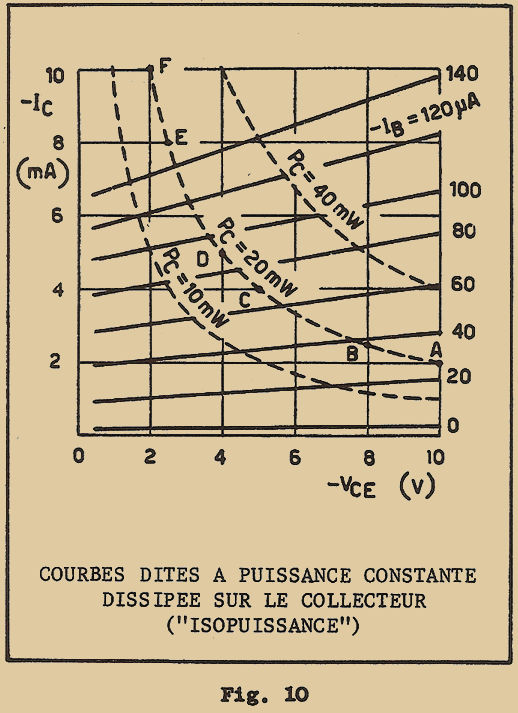
A titre d’exemples je vous donne sur la figure 10, les courbes correspondant à 10mW et 40mW. On voit qu’en augmentant la valeur de P_C, la courbe correspondante s’éloigne de l’origine des axes (elle se déplace donc vers la droite). Ceci signifie donc, que pour tous les points de fonctionnement situés dans la zone comprise entre les deux axes et une certaine courbe à puissance constante, la puissance dissipée sur le collecteur est inférieure à la puissance relative à cette courbe.

Pour être certain que la puissance dissipée sur le collecteur ne dépasse pas la valeur limite P_C max, il suffira de tracer la courbe à puissance constante limite P_Cmax et de faire en sorte que le point de fonctionnement correspondant ne dépasse jamais cette courbe.

A la figure 11, je vous ai dessiné les caractéristiques relatives à un transistor BF de faible puissance, où ont été reportées les différentes limites de courant maximum, de tension maximum et de puissance maximum de dissipation sur le collecteur.

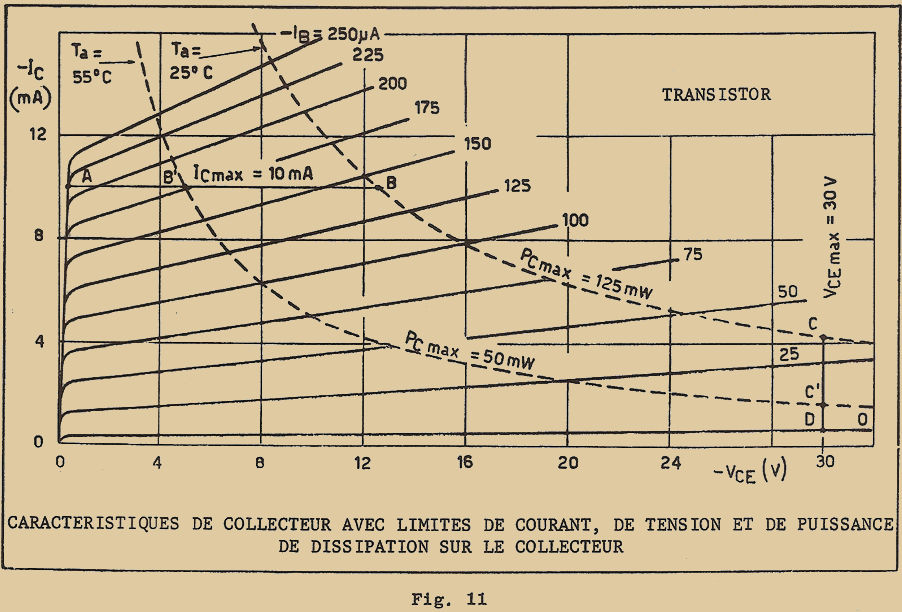
Pour une température ambiante de 25°C, on a P_C max = 125mW et la zone utile pour le choix des points de fonctionnement est délimitée par les points 0 A B C D.

Cette zone se réduit rapidement lorsque la température ambiante augmente à cause de la diminution rapide de P_C max. On voit ainsi que pour Ta = 55°C, P_C max est de 50mW seulement et la zone est réduite aux points 0 A B’ C’ D’.

Après avoir délimité la zone de fonctionnement normal on peut choisir le point de fonctionnement, en veillant à ne jamais dépasser les valeurs maxima admises.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 9^ème LEÇON THÉORIQUE

1 – On appelle famille de courbes caractéristiques de sortie l’ensemble des courbes tracées pour différentes valeurs de courant (ou de tension) de commande

2 – Pour un transistor en montage base commune, la famille de courbes la plus importante est V_CB – I_C avec I_E comme paramètre.

3 – Les courbes caractéristiques V_CB – I_C ayant I_E comme paramètre se présentent comme autant de droites pratiquement horizontales à droite de l’axe vertical qui décroissent rapidement à gauche de cet axe.

4 – Les caractéristiques mutuelles I_C – I_E ayant comme paramètre V_CB sont pratiquement superposées l’une à l’autre, parce que le courant de collecteur dans le cas du montage en base commune dépend très peu de la tension appliquée au collecteur.

5 – Dans le montage en base commune, les caractéristiques sont pratiquement horizontales et s’étendent aussi à gauche de l’axe vertical. Dans le montage en émetteur commun, elles sont plus ou moins inclinées vers le haut et ne s’étendent qu’à droite de l’axe vertical.

6 – Le point de fonctionnement d’un transistor est un certain point donné sur les courbes caractéristiques qui indique que le transistor fonctionne dans des conditions bien définies.

7 – On appelle résistance de charge, la résistance placée dans la liaison du collecteur, c’est-à-dire dans le circuit de sortie.

8 – La droite de charge est la droite tracée sur les courbes caractéristiques du collecteur, qui joint le point de l’axe horizontal correspondant à la tension d’alimentation du collecteur au point de l’axe vertical qui correspond à la tension d’alimentation divisée par la résistance de charge.

9 – L’inclinaison de la droite de charge dépend de la valeur de la résistance de charge ; elle est d’autant plus inclinée sur l’axe horizontal que cette résistance est plus grande et à la limite, elle devient verticale quand la résistance de charge est nulle.

---

EXERCICES DE RÉVISION SUR LA 10^ème LEÇON THÉORIQUE

1 – Qu’appelle-t-on polariser un transistor  ?

2 – Quelles sont les approximations que l’on peut faire dans le calcul de la polarisation dans le cas d’un montage en base commune  ?

3 – Comment peut-on déterminer la valeur de I_B qui correspond à un certain point de fonctionnement sur les courbes caractéristiques sans avoir à faire appel à une interpolation  ?

4 – Qu’appelle-t-on caractéristique mutuelle dynamique  ?

5 – Pour quelles raisons la valeur maximum du courant de collecteur est-elle limitée  ?

6 – Quelles sont les trois causes qui limitent la valeur maximum de la tension de collecteur  ?

7 – Comment calcule-t-on la puissance dissipée sur le collecteur  ?

8 – Qu’appelle-t-on "résistance thermique" d’un transistor  ?

9 – Comment varie la puissance maximum dissipable sur le collecteur quand la température ambiante varie  ?

Fin de la leçon 10

---

LECON 11

1 –EFFET DE LA TEMPÉRATURE SUR LES CARACTÉRISTIQUES D’UN TRANSISTOR

Lorsque nous avons étudié les propriétés des semi-conducteurs, nous avons vu que leur résistivité, très sensible à la température diminuait rapidement lorsque le semi-conducteur était chauffé, par suite de la rapide augmentation du nombre de paires électron-trou.

Une première constatation de ce phénomène avait été vue lors de l’étude de la diode à jonction, le courant inverse qui était pratiquement indépendant de la tension inverse appliquée à la jonction, était cependant très sensible à la température et, augmentant rapidement avec celle-ci, réduisait l’efficacité de la diode. Ce n’est pas le cas par contre, pour le courant direct qui est peu sensible à l’augmentation de la température car il est constitué principalement par les porteurs majoritaires, dont la concentration est donnée surtout par le nombre d’impuretés introduites.

Etant donné que le transistor est constitué par des semi-conducteurs, il est évident que ses caractéristiques seront influencées par la température à laquelle il sera soumis. Comme d’autre part, le transistor est constitué de deux jonctions, l’une polarisée dans le sens direct, l’autre dans le sens inverse, nous voyons tout de suite que la jonction polarisée en sens inverse sera la plus affectée par les variations de température.

Dans le fonctionnement normal du transistor, la jonction polarisée en sens inverse est la jonction collecteur-base ; ainsi une élévation de la température provoquera une augmentation du courant de collecteur. Ceci est dû à deux causes différentes : a) augmentation du coefficient d’amplification de courant, b) augmentation du courant résiduel de collecteur.

C’est cette dernière cause qui est la plus importante, et on peut en première approximation, considérer que le coefficient d’amplification reste pratiquement constant avec l’augmentation de la température. Par contre, on ne peut pas négliger l’augmentation du courant résiduel, comme on le verra bientôt.

Nous allons maintenant expliquer, comment augmente le courant résiduel. Pour cela, considérons le schéma de la figure 1, où le transistor est monté en base commune ; le courant résiduel (I_CBo dans ce cas) peut être mesuré à l’aide d’un microampèremètre inséré dans la liaison du collecteur, en laissant "en l’air" la connexion de l’émetteur de façon à ce que le courant de commande soit nul. Nous supposons d’autre part, que nous avons un thermomètre précis indiquant exactement la température à laquelle se trouve le transistor.

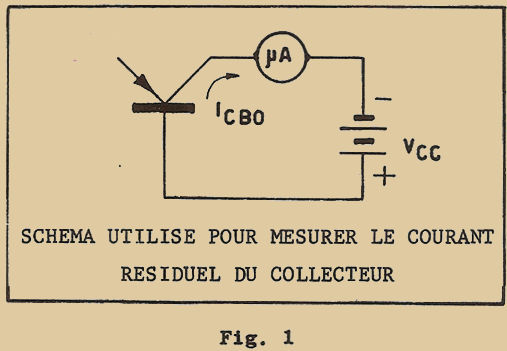
En partant de la température ambiante, par exemple 25°C, élevons progressivement la température du transistor : nous allons constater une croissance d’abord lente, puis de plus en plus rapide du courant I_CBo.

Nous verrons qu’approximativement, le courant résiduel double chaque fois que la température augmente de 10°C. Par exemple si à la température de 25°C, le courant résiduel est de 5µA, à une température de 35°C (+ 10°C), le courant résiduel sera de 10µA environ.

Si nous augmentons encore la température de 10°C, soit 45°C, le courant va encore doubler et deviendra 20µA : il sera donc devenu 4 fois plus grand qu’il ne l’était à 25°C. A 55°C, il va encore doubler et deviendra égal à 40µA, c’est-à-dire 8 fois ce qu’il était à 25°C (2 x 2 x 2 = 8) ; et ainsi de suite : 80µA à 65°C, 160µA à 75°C. Il ne faut d’ailleurs pas dépasser 75°C, si le transistor est du type au germanium, car c’est la température maximum admissible.

L’allure de la courbe du courant résiduel en fonction de la température est du type de la figure 2 pour un transistor SFT 352. La courbe monte très rapidement : elle est d’allure exponentielle comme le définissent les mathématiciens.

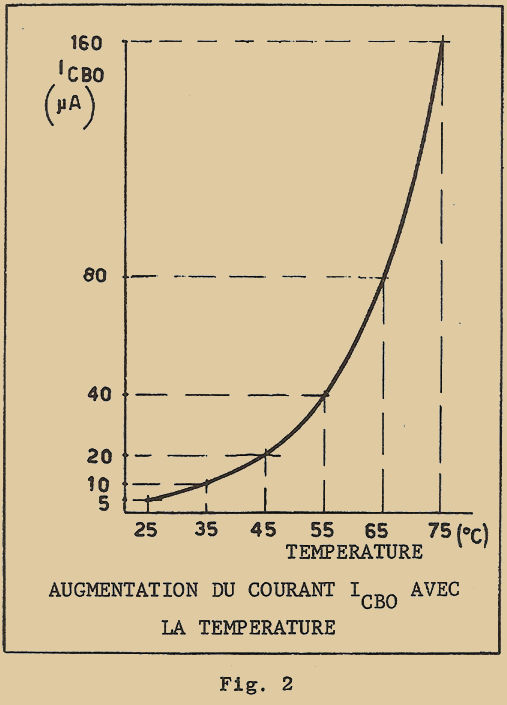
L’allure de cette courbe ne dépend pas tellement du type du transistor considéré que des propriétés même des semi-conducteurs. Ceci signifie donc, que l’allure générale sera la même pour tous les transistors, à part les valeurs des courants résiduels.

Nous pouvons alors tracer une courbe universelle, qui servira pour tous les types de transistors, en portant sur l’axe vertical, non plus les courants, (qui varient suivant le type de transistor) mais un certain coefficient H qui indique de combien de fois le courant résiduel à une température donnée, sera plus grand qu’à la température de référence de 25°C.

Etant donné, que nous avons admis que le courant résiduel doublait pour une augmentation de température de 10°C nous aurons à 25°C (température de référence), un coefficient H égal à 1. À 35°C, H = 2 ; à 45°C, H = 4 et ainsi de suite : H = 8 pour 55°C ; 16 pour 65°C ; 32 pour 75°C. Avec ces valeurs, nous pouvons tracer la courbe universelle.

Il suffit donc de connaître la valeur de I_CBo relative à 25°C (valeur qui en général, est toujours donnée par les fabricants) pour pouvoir calculer la valeur du courant résiduel à n’importe quelle autre température, au-dessus de 25°C. Ainsi par exemple, si le courant résiduel I_CBo du transistor SFT 352 est de 15µA (à 25°C), sa valeur à la température 50°C sera trouvée de la façon suivante. Nous chercherons sur le graphique de la figure 3 la valeur de H correspondante à cette température : H = 6 environ. Ceci signifie qu’à la température de 50°C, le courant résiduel sera environ 6 fois plus grand qu’à 25°C. Soit :

I_CBo (25°C) x H = 15 x 6 = 90µA

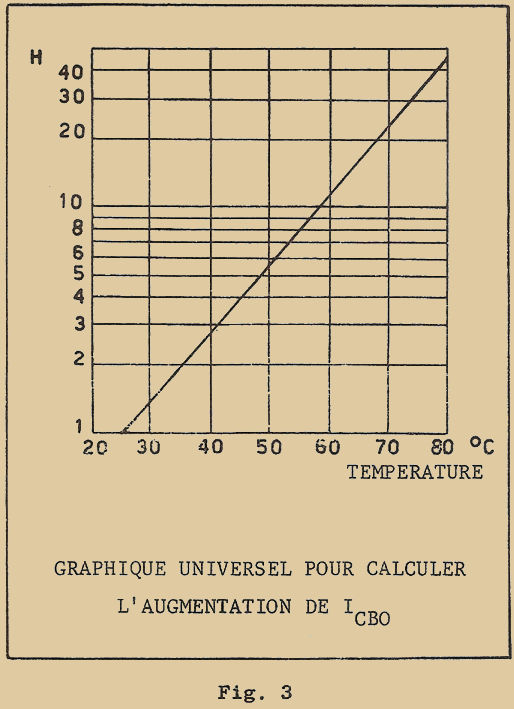
Maintenant que vous avez bien compris comment évoluait le courant résiduel en fonction de la température, nous allons étudier l’effet de cette augmentation sur le courant I_C.

Pour cela, nous examinerons séparément, le cas d’un montage en base commune et d’un montage en émetteur commun.

1 – 1 MONTAGE EN BASE COMMUNE

Lors de l’étude du montage en base commune nous avons vu que le courant de collecteur I_C pouvait être calculé par la formule suivante :

I_C = α I_E + I_CBo

c’est-à-dire qu’il était la somme d’un courant dû au courant de commande I_E et d’un courant résiduel.

Supposons que le coefficient α ne varie pas avec la température, et voyons quelle augmentation va subir le courant de collecteur lorsque nous allons élever sa température d’une certaine quantité.

Pour prendre un exemple, considérons un transistor base à la masse comme sur la figure 4-a, et dont le coefficient d’amplification soit α = 0,98. Supposons encore que la température soit de 25°C et qu’alors le courant résiduel I_CBo soit de 5µA (= 0,005mA) ; faisons traverser la connexion d’émetteur par un courant de commande I_E = 2mA.

En nous basant sur la formule précédente, le courant de collecteur sera :

I_C = 0,98 x 2 + 0,005 = 1,960 + 0,005 = 1,965mA.

Portons la température à 50°C, le courant résiduel devient 6 fois plus grand. Le courant résiduel devient donc : 5 x 6 = 30µA (0,030mA). Par conséquent, si le courant d’émetteur reste encore fixé à 2mA, le courant de collecteur devient :

I_C = 0,98 x 2 + 0,030 = 1,990mA

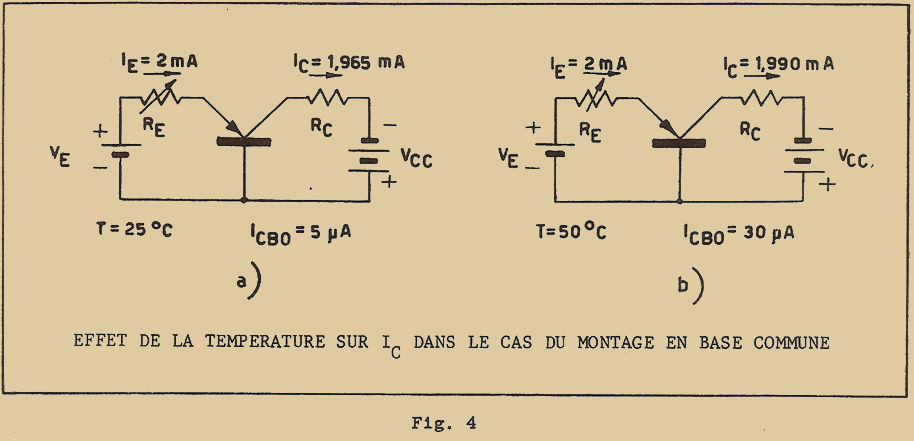
L’augmentation du courant de collecteur due à l’augmentation de la température de 25°C (50°C – 25°C) sera donnée par la différence entre les valeurs du courant de collecteur à ces deux températures.

Augmentation de I_C = 1,990 – 1,965 = 0,025mA = 25µA

(cette augmentation de I_C est évidemment la même que celle du courant résiduel I_CBo)

Nous pouvons donc dire, en toute généralité, que dans un montage en base commune, une élévation de la température provoque pour le courant de collecteur un accroissement qui est précisément celui du courant résiduel.

Etant donné d’autre part, que le courant résiduel est toujours très faible par rapport au courant de collecteur, nous pouvons en conclure qu’en première approximation, le courant I_C est peu influencé par l’augmentation de la température.

1 – 2 MONTAGE EN ÉMETTEUR COMMUN

Reprenons le même transistor que ci-dessus, et montons-le maintenant avec l’émetteur à la masse (figure 5-a). L’influence de la température sur le courant du collecteur va se manifester de façon tout à fait différente.

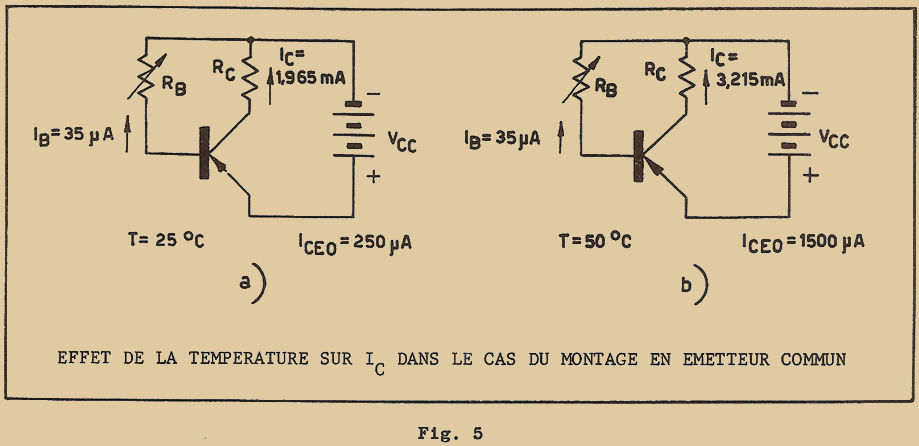
Le courant du collecteur est donné par la formule suivante (comme nous l’avons vu lors de l’étude du montage en émetteur commun).

I_C = β I_B + I_CEo

Reprenons la même variation de température de 25°C à 50°C.

Nous savons d’autre part que : β = α/(1- α)

Si α = 0,98 nous avons :

β = 0,98/(1- 0,98) = 0,98/0,02 = 49

D’autre part, nous savons aussi que : I_CEo = (β + 1) I_CBo

Si I_CBo = 5µA à 25°C, nous aurons :

I_CEo = (49 + 1) x 5 = 50 x 5 = 250µA = 0,250mA

Si l’on règle la valeur de R_B (figure 5-a) de façon à avoir un courant de base I_B = 35µA le courant de collecteur sera :

I_C = 49 x 0,035 + 0,250 = 1,715 + 0,250 = 1,965mA

c’est-à-dire la même valeur que celle dans l’exemple en base commune.

En élevant la température à 50°C, le courant résiduel I_CEo devra être calculé en fonction de I_CBo relatif à cette température.

I_CEo = (49 + 1) x 30 = 50 x 30 = 1.500µA = 1,5mA

En maintenant le courant de base à 35µA, le courant de collecteur devient :

I_C = 49 x 0,035 + 1,500 = 1,715 + 1,500 = 3,215mA

Comme vous pouvez le constater, l’effet de la température est beaucoup plus sensible dans le montage en émetteur commun. En comparant ces résultats, vous voyez que maintenant le courant de collecteur a presque doublé lorsque la température est passée de 25°C à 50°C.

Augmentation de I_C = 3,215 – 1,965 = 1,250mA

On peut démontrer que cette augmentation est (β + 1) fois plus grande que le courant résiduel I_CBo.

On vérifie en effet, qu’en multipliant par (β + 1) = 49 + 1 = 50 fois, l’accroissement du courant résiduel I_CBo calculé précédemment : I_CBo = 25µA on trouve :

50 x 25 = 1.250µA = 1,250mA

c’est-à-dire exactement la valeur que nous avons trouvée pour l’augmentation de I_C.

1 – 3 EFFET DE LA TEMPÉRATURE SUR LES CARACTÉRISTIQUES DE COLLECTEUR

Etant donné que le courant de collecteur augmente avec la température, il est évident que les courbes caractéristiques de collecteur seront-elles aussi influencées par celle-ci.

Les caractéristiques qui sont le plus influencées par la température sont celles qui correspondent au montage en émetteur commun. Nous avons vu en effet, que le courant de collecteur variait beaucoup avec la température surtout lorsque le transistor était monté en émetteur commun.

Comme dans le montage en base commune, la variation du courant collecteur est faible avec l’augmentation de la température (on peut même considérer que pratiquement, il n’y a pas de variation de courant), les courbes caractéristiques ne seront que peu perturbées par la température.

Nous n’examinerons donc que les courbes qui correspondent au montage en émetteur à la masse, car en pratique c’est le plus courant.

Nous avons vu que l’augmentation du courant collecteur était la même que celle du courant résiduel I_CEo, si le courant de base était maintenu constant. Nous supposons d’autre part, que le coefficient d’amplification de courant β reste constant.

Il est facile donc de prévoir comment les courbes caractéristiques vont se modifier avec la température : elles vont se déplacer vers le haut d’une quantité égale à l’augmentation du courant I_CEo.

En pratique, le coefficient β lui aussi augmente un peu avec la température. Il y a donc de ce fait, une dilatation plus grande entre les courbes caractéristiques car, comme nous le verrons plus loin, la distance qui sépare deux courbes successives est proportionnelle à la valeur β.

En conclusion, une élévation de la température d’un transistor, correspond à un déplacement des courbes vers le haut, et à une dilatation de celles-ci : voyez la figure 6 où je vous ai représenté les courbes relatives à une température de 25°C (figure 6-a) et 55°C (figure 6-b).

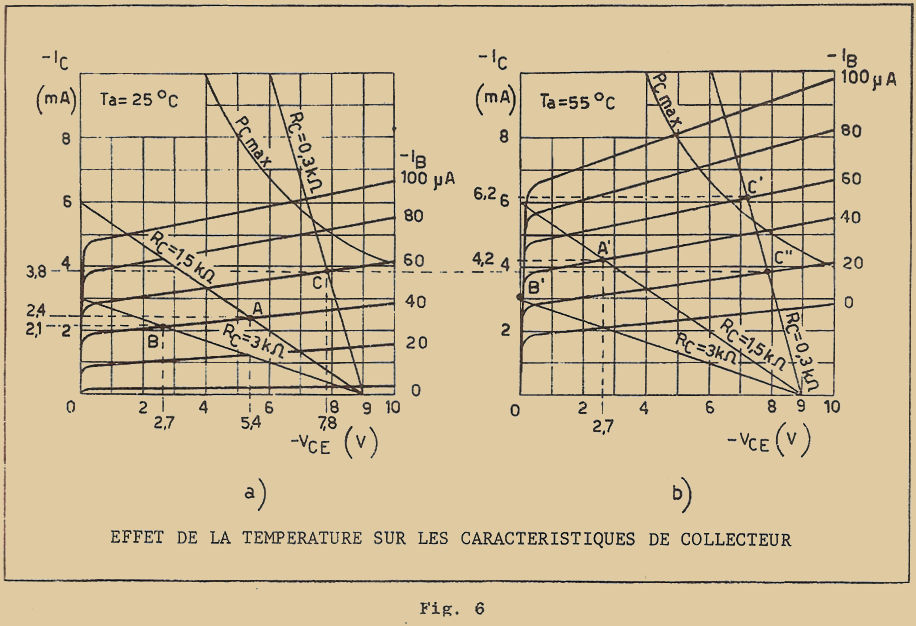
En étudiant les caractéristiques de la figure 6, il est très intéressant de remarquer comment se déplace le point de fonctionnement lorsque la température s’élève de 25°C à 55°C et d’essayer de découvrir une méthode très simple, pour réduire à des limites tolérables, l’influence de la température sur le déplacement du point de fonctionnement, c’est-à-dire sur la valeur du courant de collecteur.

Considérons le circuit de la figure 7-a. Le point de fonctionnement, à la température de 25°C peut être facilement déterminé sur les caractéristiques de la figure 6, en traçant la droite de charge R_C = 1,5 kΩ et en considérant la valeur du courant de polarisation

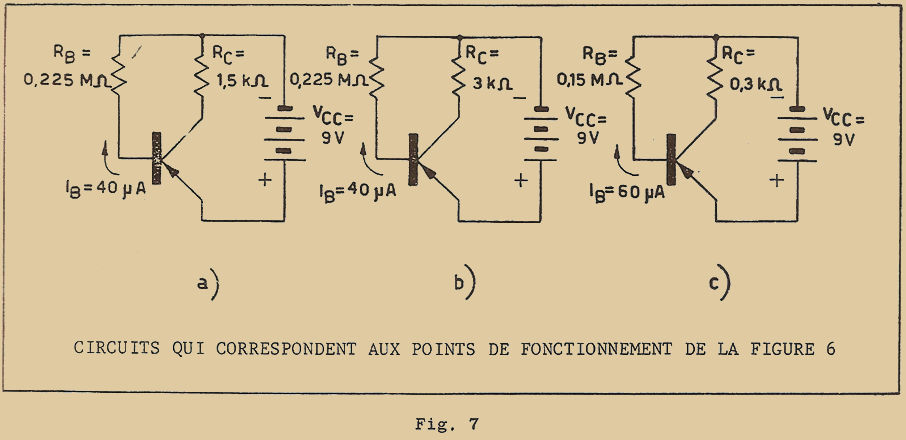
I_B = V_CC/R_B

Dans le cas de notre exemple, nous avons : I_B = (9 V)/(0,225 MΩ) = 40µA et le point de fonctionnement vient en A (figure 6-a), c’est-à-dire à l’intersection de la droite de charge et de la courbe I_B = 40µA.

Pour déterminer le point de fonctionnement à la température 55°C, il suffit de tracer la même droite de charge (1,5 kΩ) sur les caractéristiques de la figure 6-b et de prendre son intersection sur la courbe I_B = 40µA. Le nouveau point d’intersection est A’.

Nous voyons que le courant de collecteur est passé de 2,4mA à 4,2mA tandis que la tension du collecteur passait de 5,4 V à 2,7 V : dans cet exemple, le déplacement du point de fonctionnement peut ne pas avoir de conséquence néfaste sur le fonctionnement du transistor.

Par contre, dans d’autre cas, le déplacement du point de fonctionnement peut être désastreux pour les deux raisons suivantes :

Considérons le schéma de la figure 7-b qui diffère de celui de la figure 7-a par le changement de la valeur de la résistance de charge R_C qui devient maintenant 3 kΩ. Le point de fonctionnement sera déterminé en traçant la droite de charge pour 3 kΩ et par le même courant de polarisation fixé à 40µA. Ce point est maintenant B sur la figure 6-a (à 25°C).

Si la température s’élève à 55°C, le point de fonctionnement passe en B’ (figure 6-b), c’est-à-dire dans la zone de saturation, car la droite de charge ne coupe plus la courbe I_B = 40µA.

Dans ces conditions, il n’y a bien sûr pas de danger de destruction du transistor, car le point de fonctionnement se trouve en dessous de la courbe Pcmax, mais il devient évident que le transistor ne peut plus fonctionner comme un véritable amplificateur, car il se trouve dans une zone de saturation.

Un autre cas est celui qui est illustré dans le schéma de la figure 7-c et est caractérisé par une valeur de R_C très faible, comme c’est le cas dans les montages où le collecteur est relié au primaire d’un transformateur BF ou HF.

Dans cet exemple, la droite de charge a été tracée pour R_C = 0,3 kΩ et le point de fonctionnement sera défini par le courant de polarisation de la base, dont la valeur est :

I_B = (9 V)⁄(0,15 MΩ) = 60µA

A 25°C, le point de fonctionnement est en C (figure 6-a), tandis qu’à 55°C il est en C’ (figure 6-b).

On peut remarquer que si le point C était en dessous de la courbe P_Cmax, il n’en est plus de même pour le point C’. Le déplacement du point de fonctionnement place maintenant le transistor dans une zone interdite où la puissance dissipée sur le collecteur dépasse la valeur maximum admise. Dans ces conditions le transistor est détruit irrémédiablement.

Pour telle ou telle autre raison, nous ne pouvons donc admettre un déplacement du point de fonctionnement avec la température.

Pour éviter de tels inconvénients, nous avons deux solutions possibles : ou bien empêcher purement et simplement que la température du transistor n’atteigne 55°C (ce qui n’est pas toujours possible), ou bien utiliser un schéma plus complexe que celui de la figure 7 en ce qui concerne la polarisation de façon à neutraliser en partie l’effet de la température.

2 – STABILISATION THERMIQUE ET COEFFICIENT DE STABILITÉ

En observant la figure 6-b, nous voyons qu’il existe une méthode simple pour éviter que l’élévation de la température ne provoque une augmentation du courant de collecteur. En effet, si nous prenons le cas de la figure 7-c, nous voyons que le point de fonctionnement se déplace de C (figure 6-a) en C’ (figure 6-b) quand la température passe de 25°C à 55°C et le courant collecteur augmente de 3,8mA à 6,2mA.

Si nous désirons, qu’à la température de 55°C, le courant de collecteur reste fixé à sa valeur de 3,8mA, il suffit de faire en sorte qu’avec l’augmentation de la température, il y ait réduction du courant de base.

En effet, si dans le cas de l’exemple, le courant de base était ramené à la valeur de 20µA lorsque la température est devenue 55°C, le courant collecteur n’aurait pas varié.

La réduction du courant de base de 60µA à 20µA doit évidemment survenir d’une façon automatique et progressive avec l’élévation de la température et si la température venait à décroître, le courant de base devrait augmenter graduellement de façon à maintenir constant le courant de collecteur.

Cette correction automatique de la valeur du courant de collecteur est obtenue en utilisant des circuits de polarisation particuliers qui vont être décrits. Afin d’évaluer leur aptitude à réduire les variations du courant de collecteur (il n’est pas possible en effet en pratique d’annuler complètement ces variations), on introduit un coefficient que l’on appelle coefficient de stabilité.

Ce coefficient de stabilité (qui dépend non seulement du type du montage utilisé, mais aussi des valeurs des éléments qui le constituent) est indiqué par la valeur S et défini comme suit :

S = (accroissement de I_C)/(accroissement de I_CBo )

Ce coefficient S indique de combien de fois l’accroissement du courant I_C dû à une certaine élévation de la température, est plus grand que l’accroissement correspondant du courant résiduel I_CBo.

En nous rappelant ce que nous avons vu plus haut (que dans un montage en base commune, l’augmentation de I_C était égale à l’augmentation de I_CBo), nous en déduisons que pour un tel montage, la valeur de S est égale à 1. Pour un circuit en montage émetteur à la masse, l’augmentation de I_C est égale à (β + 1) fois celle du courant résiduel I_CBo : S sera égal à (β + 1). Ainsi, dans l’exemple de la figure 5, nous aurons un coefficient de stabilité :

S = 49 + 1 = 50 (puisque β = 49)

Pour les circuits en utilisation normale, la valeur de S doit être comprise entre un minimum de 5 et un maximum de 20, (ou plus) selon les exigences demandées, c’est-à-dire selon l’augmentation que l’on peut admettre au courant collecteur.

Ainsi comme nous l’avons vu pour le circuit de la figure 5, lorsque la température passe de 25°C à 50°C, l’augmentation de I_CBo est de 25µA (= 0,025mA). Si l’on admet une augmentation correspondante de I_C de 0,5mA, il faudra que le circuit de polarisation ait un coefficient de stabilité de :

S = (accroissement de I_C)/(accroissement de I_CBo ) = 0,5/0,025 = 20

Si l’on admet au contraire que l’augmentation de I_C ne doit pas dépasser 0,15mA, le coefficient S devra avoir une valeur plus faible :

S = 0,15/0,025 = 6

Des conditions plus sévères devront être appliquées lorsqu’il s’agira de circuits amplificateurs de puissance, pour éviter que le transistor ne "s’emballe" ; nous reviendrons sur ce sujet, lorsque nous étudierons les amplificateurs BF de puissance.

Tous les circuits utilisés pour la stabilisation thermique du point de fonctionnement font appel à la contre-réaction.

Etant donné, que de tels circuits tendent à maintenir constant le courant de collecteur, quelle que soit la cause qui tente de le faire varier, il faut remarquer qu’ils interviennent aussi si la variation du courant est dûe non à la température, mais au remplacement d’un transistor par un autre. En effet, il faut souligner, que des transistors d’un même type peuvent avoir des caractéristiques assez différentes et que leur remplacement peut entraîner une variation inadmissible du courant de repos.

En conclusion, l’avantage des circuits de polarisation "stabilisés" est double : non seulement ils évitent de fortes variations du courant de repos lorsque la température vient à changer, mais aussi lorsque l’on remplace un transistor par un autre, ils rendent le circuit moins sensible aux tolérances des caractéristiques des transistors.

2 – 1 STABILISATION PAR CONTRE-RÉACTION DE COLLECTEUR

Le schéma le plus simple d’un circuit de polarisation stabilisé est celui de la figure 8 qui diffère du précédent (figures 5 et 7) : en effet, la résistance R_B est maintenant reliée au collecteur, au lieu d’être directement branchée au pôle négatif de la pile.

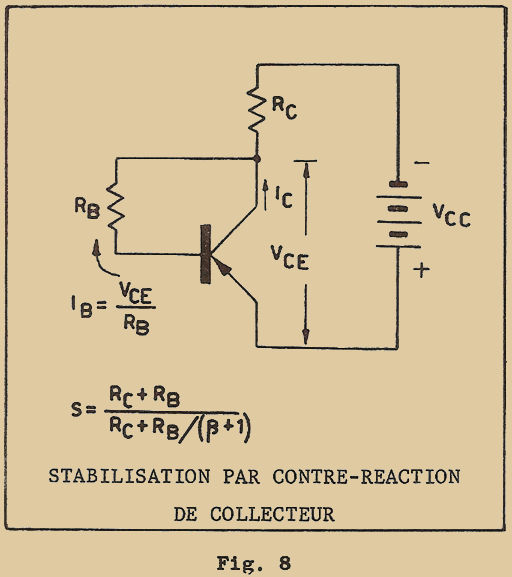
De cette manière, si pour une raison quelconque (en particulier si la température s’élève), le courant de collecteur augmente, le courant de base va diminuer automatiquement, s’opposant ainsi à une augmentation ultérieure du courant de collecteur.

En effet comme on peut le voir clairement sur les caractéristiques de la figure 6, lorsque le courant de collecteur augmente, le point de fonctionnement (par exemple A) glisse sur la droite de charge vers la gauche et par conséquent la tension de collecteur V_CE diminue.

Si la tension qui alimente la résistance R_B diminue, le courant I_B qui la traverse, diminue d’autant. Mais une diminution de I_B correspond à une diminution de I_C : on a ainsi obtenu une action qui s’oppose à l’augmentation de I_C : c’est une contre-réaction.

Par un raisonnement analogue, on peut voir que cette contre-réaction se manifeste aussi pour une diminution de I_C et, dans ce cas, on constate une augmentation de I_B. Nous en concluons donc que le circuit de la figure 8 a la propriété de s’opposer à une variation quelconque du courant collecteur, c’est-à-dire qu’il tend à maintenir constant le courant I_C.

L’aptitude du circuit à maintenir constant le courant de collecteur e

st exprimée par la valeur du coefficient S, qui pour un tel circuit peut être déterminée par la formule suivante :

S = (R_C + R_B)/(R_C + R_B/((β + 1)))

Pour mieux nous rendre compte de l’action de stabilisation du circuit de la figure 8, nous allons considérer deux exemples, relatifs aux schémas de la figure 9.

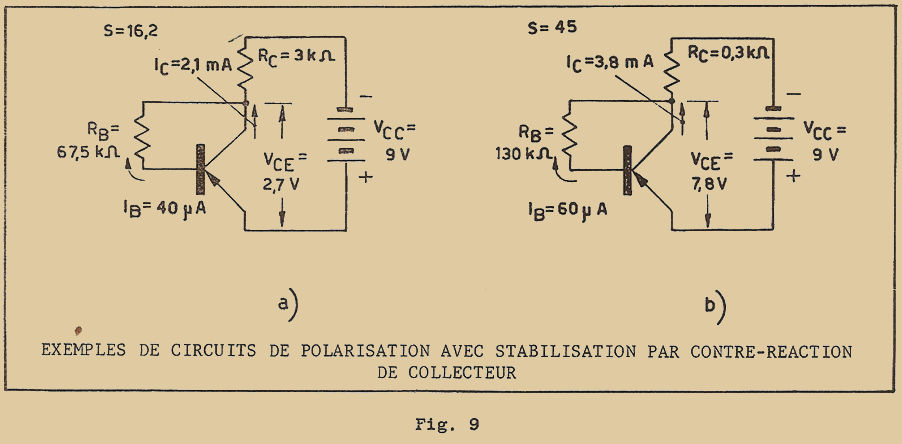
Le schéma de la figure 9-a, est dérivé de celui de la figure 7-b et fait travailler le transistor au point B de la figure 6-a. La valeur de R_C est toujours de 3 kΩ, tandis que la valeur de R_B doit être calculée de façon à avoir I_B = 40µA. Comme V_CE = 2,7 V, nous aurons :

R_B = V_CE/I_B = (2,7 V)/(40µA) = 0,0675 MΩ = 67,5 kΩ

Si β = 49, β + 1 = 50

et R_B⁄((β+1)) = 67,5 : 50 = 1,35 kΩ

La valeur du coefficient de stabilité a donc pour valeur :

S = (R_C + R_B)/(R_C + R_B/((β + 1))) = (3+67,5)/(3+1,35) = 70,5/4,35 = 16,2

ce qui signifie que si la température s’élève de 25°C à 50°C et si l’augmentation de I_CBo est de 25µA, l’augmentation correspondante de I_C sera :

accroissement de I_C = S x accroissement de I_CBo = 16,2 x 25µA = 405µA = 0,405mA

Une telle augmentation n’est que le tiers environ de celle que l’on a avec le circuit de la figure 7-b à égalité d’augmentation de la température. En effet, dans ce dernier cas, nous avions : S = (β + 1) = 50 et l’augmentation de I_C était : 50 x 25µA = 1.250µA = 1,25mA

En ce qui concerne le circuit de la figure 9-b, dérivé de celui de la figure 7-c, la valeur de R_B nécessaire pour faire travailler le transistor au point C (figure 6-a), doit être déterminée de façon à avoir un courant de base de 60µA. Comme la tension V_CE est maintenant de 7,8 V, nous aurons :

R_B = V_CE/I_B = (7,8 V)/(60µA) = 0,13 MΩ = 130 kΩ

d’où R_B⁄((β+1)) = 130/50= 2,6 kΩ

et comme R_C = 0,3 kΩ, nous aurons :

S = (0,3+130)/(0,3+2,6) = 130,3/2,9 = 45 environ

Nous remarquons tout de suite, que dans ce cas, le circuit présente une stabilisation insuffisante, car la valeur de S est encore très élevée (45 contre 50 pour un circuit non stabilisé). Ceci est dû au fait que R_C a une valeur très faible par rapport au premier cas (0,3 kΩ au lieu de 3 kΩ). Ainsi, l’effet de contre-réaction de collecteur est faible, car faible est la chute de tension produite aux bornes de R_C par le courant de collecteur.

En conclusion, nous pourrons dire que le circuit de polarisation par stabilisation du point de fonctionnement par contre-réaction de collecteur, n’est valable que si R_C est élevée. Un tel circuit n’est donc pas adapté dans le cas où le collecteur est chargé par un transformateur BF ou HF, dont la résistance d’enroulement primaire est très faible.

Une règle pratique pour savoir si un tel circuit peut être utilisé est de calculer la tension de collecteur correspondant au point de fonctionnement qui doit être inférieur à la moitié de la tension V_CC délivrée par la pile. Dans le cas contraire, si on désire une bonne stabilité on devra faire appel à d’autres types de circuits.

2 – 2 STABILISATION PAR CONTRE-RÉACTION D’ÉMETTEUR

Un autre type de circuit dont la propriété est de maintenir constant le courant de collecteur est illustré à la figure 10-a. Dans ce cas, la contre-réaction est obtenue en intercalant une résistance R_E, de valeur appropriée dans la connexion d’émetteur.

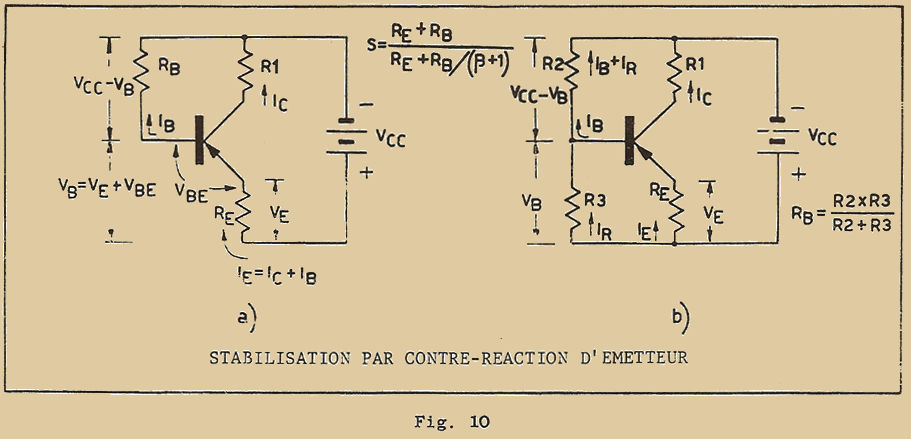
Pour voir comment se manifeste la contre-réaction, il suffit de remarquer que le courant de base est déterminé par la valeur de R_B et par la valeur de la tension qui s’établit aux bornes mêmes de R_B, et que cette tension est d’autant plus faible que plus élevé est le courant d’émetteur.

En effet, l’émetteur est polarisé à la tension V_E = R_E x I_E et ainsi la base se trouve à la tension VB = V_E + V_BE ; la tension aux bornes de R_B sera alors donnée par la différence entre la tension fournie par la pile et la tension de la base, c’est-à-dire aura comme valeur V_CC - VB. Si le courant I_C augmente, V_E augmentera aussi, ainsi que VB ; en conséquence, la valeur V_CC – VB va diminuer ainsi que le courant I_B, puisque

I_B = (V_CC - V_B)/R_B

La contre-réaction, dont dépend la stabilisation est donc dûe à l’augmentation de la tension d’émetteur qui asservit le courant de polarisation de la base.

L’efficacité du circuit sera d’autant plus grande que plus élevée sera la valeur de R_E. Le coefficient de stabilité est donné par la formule aussi simple que précédemment :

S = (R_E + R_B)/(R_E + R_B/((β + 1)))

Pour obtenir des valeurs faibles de S (c’est-à-dire pour avoir une bonne stabilité), il faut utiliser des résistances d’émetteur relativement élevées, de façon que la tension V_E soit environ la moitié de la tension d’alimentation de la pile. Ceci est un inconvénient notable, car on doit utiliser une pile dont la tenson soit environ le double de ce qui serait nécessaire pour un circuit non stabilisé ; d’autre part, dans des circuits de puissance, la puissance dissipée dans la résistance est très élevée, et le rendement de l’amplificateur est mauvais.

Les raisons précédentes font que le circuit de la figure 10-a n’est utilisé que dans des amplificateurs de faible puissance, ou lorsque l’on n’a pas besoin d’avoir une faible valeur de S, ou bien dans des circuits spéciaux.

Dans les circuits amplificateurs classiques, et en particulier dans les amplificateurs de puissance, on admet que la tension aux bornes de la résistance d’émetteur est au maximum de l’ordre de un ou de deux dixièmes de la tension d’alimentation. Dans ces conditions, il est possible d’obtenir une bonne stabilité, en modifiant le circuit de la figure 10-a comme indiqué à la figure 10-b.

La différence essentielle est que maintenant la base est alimentée, non plus par l’intermédiaire de la résistance R_B, mais par un pont de résistance R₂/R₃. De cette façon, on peut obtenir des valeurs faibles de S, avec de faibles valeurs de R_E.

La formule qui permet de calculer le coefficient de stabilité S est la même que pour le circuit de la figure 10-a, sauf que maintenant R_B est donnée par la mise en parallèle de R₂ et R₃.

R_B = (R₂ x R₃)/(R₂ + R₃ )

Dans le circuit d’alimentation de la base, nous avons 2 courants distincts : I_R qui traverse R₃ et (I_B + I_R) qui traversent R₂. Du choix de la valeur de I_R dépendent les valeurs de R₂ et R₃ et donc de S. Pour obtenir de faibles valeurs pour S, c’est-à-dire comprises entre 15 et 5, il faut grosso modo, prendre I_R, 5 à 10 fois plus grand que I_B.

Les exemples qui vont suivre, permettront de bien comprendre comment calculer les circuits de stabilisation par contre-réaction d’émetteur et comparer ainsi les résultats avec les types déjà vus.

Supposons par exemple (figure 11-a) que nous voulons faire travailler le transistor au point A de la figure 6-a en utilisant une pile d’alimentation de 9 V et le circuit de la figure 10-a. Il faut remarquer tout de suite que la résistance de charge R_C n’est plus seulement celle qui est placée dans la connexion du collecteur, mais elle s’ajoute maintenant avec celle qui est placée dans l’émetteur :

R_C = R₁ + R_E

En effet R₁ et R_E se trouvent en série, et on considère qu’elles sont parcourues par le courant I_C.

Nous voyons ainsi que l’approximation faite en son temps, et qui consistait à négliger la tension entre base et émetteur V_BE, était tout à fait valable, et nous pouvons retenir que I_E est pratiquement égal à I_C, sachant que I_B est très faible.

Avec ces approximations, les formules rigoureuses vues précédemment se simplifient et deviennent :

V_E = R_E x I_C I_B = (V_CC - V_E)/R_B

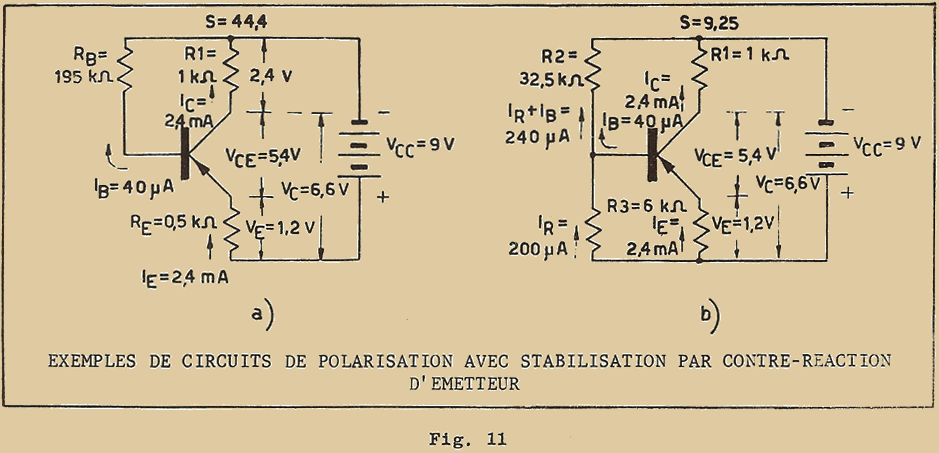
De là, nous pouvons tirer les valeurs de R_E et R_B :

R_E = V_E/I_C et R_B = = (V_CC - V_E)/I_B

On peut déterminer R_E si l’on connait le courant I_C relatif au point de fonctionnement (I_C = 2,4mA pour le point A de la figure 6-a), en prenant pour V_E une valeur convenable. Si la tension d’alimentation est V_CC = 9 V, on peut choisir pour V_E une valeur de l’ordre de 1,2 V, valeur comprise entre les limites énoncées plus haut, c’est-à-dire de 1 à 2 dixièmes de la valeur de la tension d’alimentation.

D’où : R_E = V_E/I_C = 1,2/2,4 = 0,5 kΩ

Etant donné que dans l’exemple de la figure 6-a, la valeur de R_C est de 1,5 kΩ on peut en déduire la valeur de R₁, en se rappelant que R_C, dans le cas de la figure 10-a, est la somme de R₁ et de R_E : on a donc :

R₁ = R_C – R_E = 1,5 – 0,5 = 1 kΩ

La détermination de la valeur de R_B est immédiate, sachant que pour le point de fonctionnement considéré, le courant de base est 40µA.

R_B = = (V_CC - V_E)/I_B = (9-1,2)/40 = 7,8/40 = 0,195 MΩ = 195 kΩ

Il ne reste plus qu’à calculer la valeur de S en tenant compte de ce que :

R_E = 0,5 kΩ ; R_B = 195 kΩ ; β + 1 = 50

d’où :

R_B/((β+1)) = 195/50 = 3,9 kΩ

Le coefficient de stabilité S est donc :

S = (R_E + R_B)/(R_E + R_B/((β + 1))) = (0,5+195)/(0,5+3,9) = 195,5/4,4 = 44,4 environ

Un résultat bien différent est obtenu avec le circuit de la figure 10-b.

En effet, (figure 11-b) si l’on choisit le même point de fonctionnement et la même valeur de R_E (0,5 kΩ), les résistances R₂ et R₃ pourraient être déterminées en fixant la valeur de I_R et en prenant les formules suivantes :

R₂ = (V_CC - V_B)/(I_R+ I_B) ; R₃ = V_B/I_R

R₂ et R₃ seront exprimées en kΩ, si les tensions le sont en volts et les courants en milliampères.

Ces formules deviennent avec les approximations admises (c’est-à-dire en négligeant V_BE) :

R₂ = (V_CC - V_E)/(I_R+ I_B) ; R₃ = V_E/I_R

Si l’on fixe la valeur de I_R à 5 fois celle de I_B (I_B = 40µA) on aura :

I_R = 5 x 40 = 200µA = 0,2mA. D’où :

R₂ = (V_CC - V_E)/(I_R+ I_B) = (9-1,2)/(0,2+0,04) = 7,8/0,24 = 32,5 kΩ et R₃ = V_E/I_R = 1,2/0,2, = 6 kΩ

Pour calculer la valeur de S, il suffit de prendre la formule vue précédemment, en se rappelant que R_B est :

R_B = (R₂ x R₃)/(R₂ + R₃ ) = (32,5 x 6)/(32,5+6) = 195/38,5 = 5,06 kΩ

Comme (β + 1) = 50, il en résulte R_B / (β + 1) = 5,06 / 50 = 0,101 kΩ

S = (R_E + R_B)/(R_E + R_B / (β + 1)) = (0,5+5,06)/(0,5+0,101) = 5,56/0,601 = 9,25

L’augmentation du courant de collecteur sera maintenant (on admet toujours que la température s’élève de 25°C et que l’augmentation correspondante de I_CBo est toujours de 25µA).

Accroissement de I_C = S x accroissement de I_CBo = 9,25 x 25 = 231µA = 0,23mA ce qui correspond à environ 10 % du courant collecteur (I_C = 2,4mA).

Si nous voulons obtenir des valeurs de S (c’est-à-dire l’accroissement de I_C) encore plus faibles, il suffira de choisir pour I_R des valeurs plus élevées, par exemple 8 ou 10 fois la valeur de I_B, et refaire les calculs ci-dessus.

Remarquons que dans les deux exemples de la figure 11, la tension V_CE = 5,4 V correspondant au point de fonctionnement choisi, reste la même : c’est la tension qui existe entre le collecteur et l’émetteur. La tension de la pile se répartit ainsi : 1,2 V aux bornes de R_E, 5,4 V aux bornes du transistor, 2,4 V aux bornes de R₁.

La tension de collecteur V_C, c’est-à-dire la tension qui s’établit entre le collecteur et la masse, n’est autre que la somme de la tension V_E et de la tension V_CE ; dans le cas de l’exemple elle est égale à :

V_C = V_E + V_CE = 1,2 + 5,4 = 6,6 V

2 – 3 STABILISATION PAR THERMISTANCE.

On peut stabiliser différemment le point de fonctionnement d’un transistor en utilisant une résistance spéciale (figure 12) qui a la propriété de présenter une résistance dont la valeur décroît lorsque sa température s’élève. On l’appelle thermistance. Une telle propriété peut être obtenue en réalisant la thermistance avec des semi-conducteurs ou bien avec des agglomérés résistants comme pour les résistances classiques.

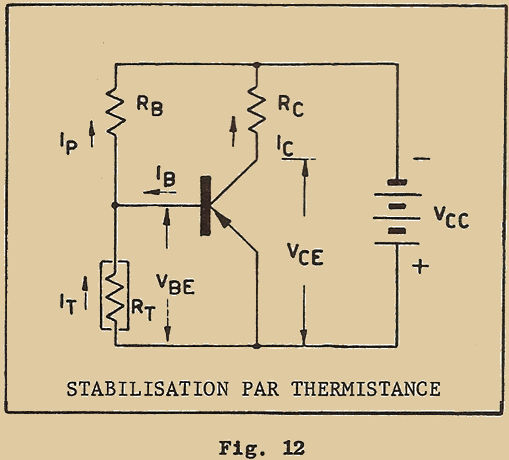
Le circuit de la figure 12 est obtenu à partir d’un circuit normal non stabilisé et en plaçant une thermistance de valeur convenable en parallèle sur les connexions de base et d’émetteur du transistor, comme on peut le voir sur la figure où la thermistance> est indiquée par R_T. Son symbole est celui d’une résistance dans un rectangle.

Pour comprendre le fonctionnement d’un tel circuit, il suffit de se rappeler que la tension V_BE est petite par rapport à la tension d’alimentation V_CC et que le courant de polarisation I_P n’est déterminé pratiquement que par les valeurs de V_CC et R_B. Il reste pratiquement constant malgré les variations de R_T et de V_BE provoquées par la variation de la température.

D’autre part, il faut remarquer que le courant I_B qui polarise le transistor et le courant I_T qui traverse la thermistance, s’ajoutent pour former le courant I_P.

Il est donc évident, que si la valeur de R_T diminue lorsque la température s’accroît, le courant I_P passera de préférence par R_T, en trouvant un chemin de résistance plus faible qu’à travers le transistor et ainsi la valeur de I_T va augmenter. En conséquence, le courant I_B va diminuer, car la somme I_B + I_T doit rester constante et égale à I_P.

Le résultat final est une diminution de I_B lorsque la température augmente. Un tel circuit est particulièrement indiqué dans le cas où l’on ne peut prendre pour R_E une valeur élevée. A fortiori, dans le cas où l’on ne peut pas utiliser de résistance d’émetteur, un tel circuit rend de grands services. Par exemple dans les étages de sortie BF (étages de puissance), on utilise très souvent des thermistances pour stabiliser les transistors.

Pour que ce circuit soit efficace, il faut placer la thermistance au voisinage des transistors de puissance, de façon qu’elle suive bien leurs variations de température.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 10^ème LEÇON THÉORIQUE

1 – Polariser un transistor signifie le faire travailler en un point déterminé de la caractéristique de collecteur.

2 – Dans le calcul du circuit de polarisation en montage base à la masse, on peut admettre que le courant de collecteur est sensiblement égal au courant d’émetteur, et négliger la tension qui s’établit entre l’émetteur et la base.

3 – Pour éviter de faire une interpolation dans le calcul de I_B, il suffit de faire appel à la caractéristique mutuelle de courant.

4 – La caractéristique mutuelle dynamique est une caractéristique mutuelle particulière qui correspond à une droite de charge donnée au lieu que ce soit à une valeur de tension de collecteur donné.

5 – La valeur maximum du courant de collecteur est limitée par la section de la jonction collecteur-base et aussi parce que le coefficient β diminue lorsque I_C croît.

6 – La valeur maximum de la tension de collecteur est limitée, ou par l’effet Zener, ou par l’effet d’avalanche, ou encore par l’effet d’annulation de la base.

7 – La puissance dissipée sur le collecteur peut être calculée par le produit de la tension entre collecteur et émetteur (ou la base) par le courant de collecteur.

8 – La "résistance thermique" est un coefficient qui exprime de combien de degrés augmente la température de la jonction pour chaque milliwatt de puissance dissipée sur le collecteur.

9 – Lorsque la température ambiante augmente, la puissance maximum de dissipation possible sur le collecteur diminue rapidement.

---

EXERCICES DE RÉVISION SUR LA 11^ème LEÇON THÉORIQUE

1 – Pourquoi le courant résiduel I_CBo est-il influencé par la température du transistor  ?

2 – Quelle est la loi approximative que suit I_CBo lorsque la température augmente  ?

3 – Quel est le montage dans lequel le courant de collecteur est surtout influencé par la température  ?

4 – Quel est l’effet sur les courbes caractéristiques de collecteur, d’une augmentation de la température  ?

5 – Comment peut-on définir le coefficient de stabilité S  ?

6 – Quelles sont les valeurs de S dans un montage en base commune et en émetteur commun  ?

7 – Que signifie avoir S égal par exemple à 10  ?

8 – Comment peut-on réduire normalement l’accroissement du courant de collecteur pour le maintenir entre des limites acceptables  ?

9 – Pourquoi est-il nécessaire de stabiliser, du point de vue thermique, le point de fonctionnement d’un transistor  ?

Fin de la leçon 11

---

LECON 12

1 – PARAMÈTRES D'UN TRANSISTOR

Les courbes caractéristiques d'un transistor indiquent comme nous l'avons vu, les propriétés relatives à n'importe quel point de fonctionnement. Elles sont indispensables pour avoir une idée générale sur le comportement du transistor et servent en particulier à déterminer le point de fonctionnement qui convient le mieux et à calculer le circuit de polarisation.

Cependant il est souvent plus intéressant du point de vue calculs, d'opérer sur des nombres plutôt que de continuer à travailler sur les caractéristiques.

Les propriétés d'un transistor, relatives à un point de fonctionnement particulier, peuvent être indiquées de différentes façons en donnant un certain nombre de valeurs que l'on appelle Paramètres.

Un paramètre typique est le coefficient d'amplification (α ou β selon le type du montage) mais on voit rapidement que donné seul il ne suffit pas à exprimer d'une façon complète les propriétés d'un transistor : en effet, deux transistors, l'un de très faible puissance et l'autre de puissance plus grande, peuvent avoir un coefficient d'amplification de même valeur et présenter cependant des caractéristiques totalement différentes.

Pour schématiser d'une façon complète les propriétés d'un transistor, il faut donc donner plus d'un paramètre : en général quatre paramètres lorsqu'il s'agit d'un transistor basse fréquence, environ six pour un transistor H.F.

Dans chaque cas, les paramètres peuvent être représentés de façon différente. Le choix d'un système de paramètres, plutôt qu'un autre ne se justifie que par la simplification des calculs.

Nous prendrons surtout en considération, un système de paramètres appelés Paramètres Hybrides. Vous aurez également à étudier un système utilisé quelquefois en BF et composé des Paramètres r (résistants). Je vous donnerai enfin pour terminer, quelques indications sur les systèmes utilisés pour les transistors "haute-fréquence".

Afin de mieux comprendre la signification des paramètres hybrides il faut tout d'abord apprendre ce que signifient les notions de Résistance d'entrée et Résistance de sortie d'un transistor.

1 – 1 RÉSISTANCE D'ENTRÉE ET DE SORTIE EN COURANT CONTINU

Considérons le schéma de la figure 1 : le montage du transistor est en émetteur commun, et une seule pile est utilisée pour polariser la base et le collecteur. C'est le schéma classique que vous connaissez bien.

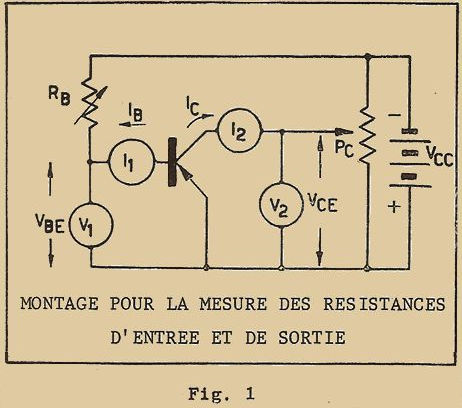
Avec le potentiomètre P_C on peut régler la tension du collecteur et avec R_B le courant de base : le transistor est amené à travailler en n'importe quel point de sa caractéristique. Le millivoltmètre V₁ et le microampèremètre I₁ mesurent la tension et le courant de la base (grandeurs d'entrée), tandis que le voltmètre V₂ et le milliampèremètre I₂ contrôlent la tension et le courant de collecteur (grandeurs de sortie).

Si l'on applique maintenant au collecteur du transistor une certaine tension V_CE et que l'on fasse traverser la base par un courant I_B, le point de fonctionnement sera ainsi déterminé. Dans ces conditions, le circuit du collecteur sera traversé par un courant I_C mesuré par I₂ et entre la base et l'émetteur il s'établira une tension V_BE mesurée par V₁.

On peut alors définir une Résistance d'entrée relative au point de fonctionnement considéré et indiquée par le symbole R_e, cette résistance étant obtenue en faisant le rapport entre la tension et le courant d'entrée, c'est-à-dire :

R_e = V_BE/I_B

Si l'on mesure la tension V_BE en mV (cette tension étant relativement faible il faut la mesurer à l'aide d'un millivoltmètre) et le courant I_B en µA la valeur de R_e sera alors exprimée en kΩ. Ainsi par exemple, si pour un courant de base de 50µA, on a une tension V_BE = 150mV, la valeur de la résistance d'entrée sera R_e = 150/50 = 3kΩ.

On peut définir de la même façon la résistance de sortie, comme étant le rapport entre la tension et le courant de sortie.

R_s = V_CE/I_C

Comme normalement la tension du collecteur se mesure en volts et le courant en milliampères, la résistance de sortie sera donnée en kΩ. Par exemple, si pour le point de fonctionnement considéré on a V_CE = 5 V et I_C = 2,5mA, la résistance de sortie R_s sera :

R_s = 5/2,5 = 2kΩ

Les résistances R_e et R_s ainsi définies sont effectivement les valeurs des résistances présentées par le transistor, c'est-à-dire que R_e est la résistance que présente le circuit de base au passage du courant I_B, et R_s est par analogie, la résistance présentée par le circuit du collecteur au courant I_C (pour un point de fonctionnement déterminé).

Comme ces résistances correspondent à des tensions continues de polarisation appliquées au transistor, on les appelle Résistances statiques (d'entrée et de sortie) ou Résistances en courant continu.

Le nom de "Résistance statique" dérive du fait que dans les conditions définies ci-dessus, on n'applique à l'électrode de commande aucun signal à amplifier : le transistor se trouve donc au "au repos" c'est-à-dire en "conditions statiques".

Les valeurs des résistances statiques d'entrée et de sortie peuvent être déterminées à l'aide des courbes caractéristiques du transistor, sans avoir à faire appel au circuit de la figure 1. Pour déterminer la résistance R_e, nous avons vu qu'il fallait connaître la tension V_BE. Cette dernière ne peut donc plus être négligée comme c'était le cas dans le calcul de la polarisation. Les familles de courbes caractéristiques de collecteur ne suffisent plus maintenant. Nous devons faire appel à d'autres courbes qui contiennent V_BE.

Les constructeurs de transistors, donnent souvent les courbes V_BE – I_B (caractéristique d'entrée) et V_BE – V_CE (courbes mutuelles de tension). Un exemple de courbes caractéristiques complètes, relatives à un certain type de transistor en montage Emetteur commun, est donné à la figure 2.

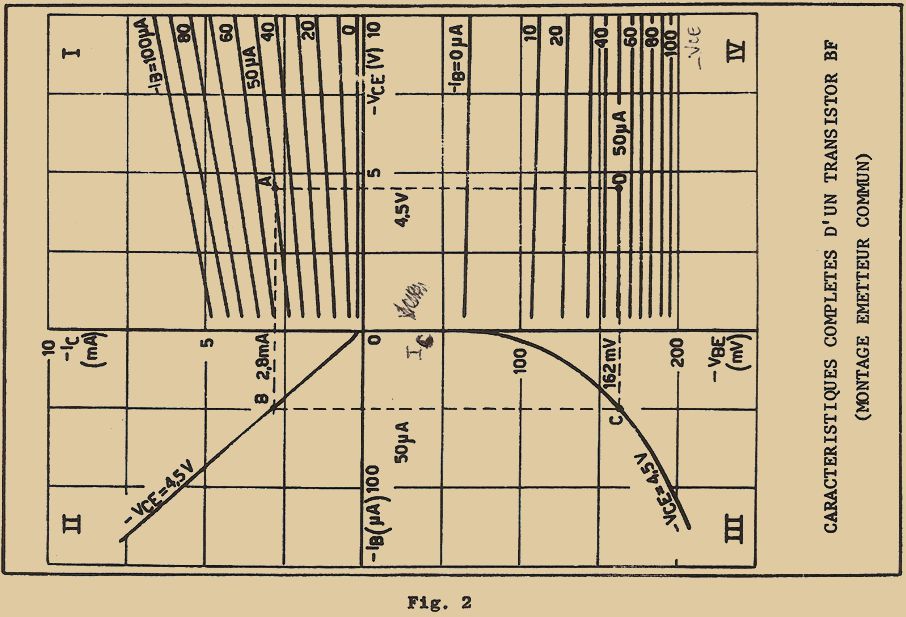
Vous voyez dans le premier quadrant (en haut à droite) les courbes caractéristiques du collecteur. Dans le deuxième quadrant (en haut à gauche), figure la caractéristique mutuelle de courant que nous avons vue dans les leçons précédentes. Une nouvelle caractéristique est reportée dans le troisième quadrant (en bas à gauche), c'est celle qui contient la tension V_BE ; c'est la caractéristique d'entrée V_BE – I_B relative à une tension de collecteur de 4,5 V. Dans le quatrième quadrant (en bas à droite) vous trouvez V_BE – V_CE avec I_B comme paramètre.

Nous disposons ainsi d'un système à quatre grandeurs V_CE, I_C, V_BE, I_B. Chacun des demi-axes est donc commun à deux quadrants adjacents.

Il faut tout d'abord, fixer le point de fonctionnement (point de repos) qui nous intéresse. Prenons un exemple. Soit le point de fonctionnement qui correspond aux valeurs suivantes : V_CE = 4,5 V et I_B = 50µA. C'est le point A du quadrant I.

Traçons maintenant l'horizontale passant par le point A. Celle-ci coupe l'axe vertical I_C au point 2,8mA. Le courant de collecteur est donc I_C = 2,8mA. La résistance de sortie est donc :

R_s = 4,5/2,8 = 1,61kΩ

Pour calculer la résistance d'entrée, il faut déterminer la tension V_BE relative à ce point de fonctionnement. Il suffit pour cela de tracer par le point A une verticale qui rencontre dans le quadrant IV, la courbe I_B = 50µA au point D. Si l'on trace maintenant par le point D, une horizontale cette dernière coupe l'axe vertical V_BE au point 162mV. La valeur de R_e est donc :

R_e = 162/50 = 3,24kΩ

Le point D du quatrième quadrant et le point A du premier représentent tous les deux le point de fonctionnement considéré avec la seule différence que dans le quadrant I on lit sur les axes de coordonnées la tension et le courant de collecteur, tandis que dans le quadrant IV, on lit encore la tension du collecteur sur l'axe horizontal et la tension de base sur l'axe vertical.

Le même point de fonctionnement peut encore être représenté dans les quadrants II et III respectivement par les points B et C. Les points B et C se trouvent sur la caractéristique V_CE = 4,5 V, ce qui signifie que le point de fonctionnement correspond bien à une tension de collecteur de 4,5 V et que le courant de polarisation de base est 50µA.

Nous pouvons donc en conclure, qu'en fixant pour un transistor le point de fonctionnement, celui-ci est représenté par quatre points distincts A, B, C, D, (figure 2), un dans chaque quadrant. Ces quatre points sont toujours disposés aux sommets d'un rectangle, dont les côtés (en pointillés sur la figure 2) coupent les quatre demi-axes aux valeurs des quatre grandeurs électriques (V_CE, I_C, V_BE, I_B) qui caractérisent le point de fonctionnement considéré.

Remarquons encore, que pour déterminer les résistances d'entrée et de sortie, deux points sont surtout intéressants : A et C. En effet en traçant par le point A une horizontale et une verticale nous lisons directement les valeurs V_CE et I_C qui déterminent R_s. De la même manière, en traçant par le point C, une horizontale et une verticale, nous trouvons V_BE et I_B nécessaires pour le calcul de R_e.

Tout ce que je viens de vous expliquer, était valable pour le montage en émetteur commun. Nous pouvons refaire le même raisonnement en ce qui concerne le montage en base commune, et déterminer une résistance d'entrée et une de sortie.

Il faut souligner que pour le montage en base commune, les grandeurs d'entrée sont la tension émetteur-base V_EB et le courant d'émetteur IE ; les grandeurs de sortie sont la tension collecteur-base VCB et le courant de collecteur I_C. Nous aurons donc :

R_e = V_EB/I_E  et  R_s = V_CB/I_C

Ces résistances peuvent encore être déterminées sur les courbes caractéristiques du transistor qui doivent correspondre maintenant au montage base à la masse. On procédera de façon analogue à ci-dessus.

1 – 2 RÉSISTANCES D'ENTRÉE ET DE SORTIE EN COURANT ALTERNATIF

Soit encore le même circuit (figure 1) et supposons que nous avons réglé R_B et P_C de façon que le transistor travaille en un certain point de sa caractéristique. Soient V'_BE, I'_B, V'_CE et I'_C les valeurs des tensions et des courants indiqués par les appareils de mesure.

Agissons sur R_B de façon à porter le courant de base, de I'_B à une valeur plus grande I''_B. La tension base-émetteur va subir une augmentation, et V₁ n'indiquera plus la valeur V'_BE mais une valeur plus grande V''_BE.

En d'autres termes, en agissant sur R_B nous provoquons une certaine augmentation du courant de base, dont la valeur est : I''_B – I'_B ce qui provoque une certaine augmentation de la tension base-émetteur : V''_BE – V'_BE.

On peut alors définir une Résistance dynamique d'entrée ou Résistance d'entrée en courant alternatif que l'on indique par r_e et qui est :

r_e = (accroissement de V_BE)/(accroissement de I_B)

Nous pouvons dire encore, que l'augmentation de I_C (provoquée par l'augmentation de I_B) détermine une diminution de la tension V_CE. C'est ce qui arrive : il faut donc avant de lire sur les appareils de mesure les valeurs I''_B et V''_BE, ramener V_CE à sa valeur initiale en agissant sur P_C. Ceci signifie donc, que les augmentations du courant et de la tension de base doivent être faites en maintenant constante la valeur de la tension du collecteur. En effet la tension du collecteur a toujours une certaine réaction sur la valeur du courant et de la tension de la base. Si nous voulons donc que les augmentations des grandeurs d'entrée ne soient pas perturbées par les variations de la tension de sortie (tension de collecteur) il nous faut maintenir cette dernière constante.

Par analogie, agissons maintenant sur P_C de façon à faire subir à la tension du collecteur, une certaine augmentation en la portant de la valeur V'_CE à V''_CE. Nous aurons donc une augmentation du courant de collecteur et aussi une augmentation du courant de base. Nous agirons donc sur R_B pour ramener le courant de base à sa valeur initiale I'_B. Nous lirons donc sur I₂, la valeur I''_C et déterminerons ainsi l'augmentation de I_C qui sera donc :

I''_C – I'_C

On peut alors définir une Résistance dynamique de sortie (ou en courant alternatif), qui sera indiqué par r_s et dont la valeur sera donnée par :

r_s = (accroissement de V_CE)/(accroissement de I_C )

Le nom de "résistance en courant alternatif" ou de "résistance dynamique" donné à la résistance d'entrée et de sortie que nous venons de définir, dérive du fait que ces valeurs sont celles que présentent le transistor au passage du courant alternatif (superposé au courant continu de polarisation) qui constitue soit le signal à amplifier appliqué à l'entrée du transistor, soit le signal amplifié prélevé à la sortie.

Vous assimilerez mieux toutes ces notions, lorsque vous aurez étudié plus tard les amplificateurs. Pour le moment, il suffit de savoir que le transistor se comporte de façon différente, selon qu'il s'agit du courant continu de polarisation, ou du courant alternatif que constitue le signal, et que les valeurs des résistances en courant continu et en courant alternatif diffèrent, peu en général, mais diffèrent toujours.

Pour se faire une idée sur les différences présentées par ces valeurs, il suffit de calculer r_e et r_s pour le même point de fonctionnement considéré dans l'exemple précédent. Nous aurons ainsi un exemple de la façon dont il faut opérer sur les caractéristiques pour déterminer les valeurs des résistances dynamiques d'entrée et de sortie.

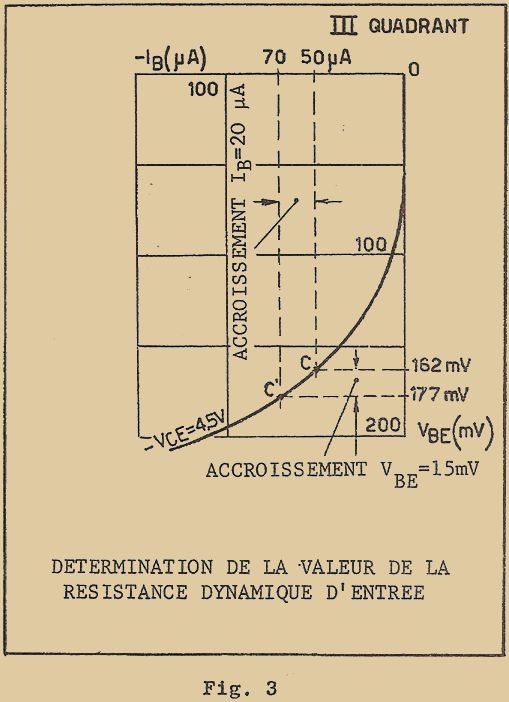
Pour déterminer r_e il faut provoquer une augmentation de I_B et voir de combien augmente V_BE en maintenant la tension de collecteur constante. Si l'on opère sur les caractéristiques d'entrée, ceci signifie que le point de fonctionnement C de la figure 2 va se déplacer sur la courbe qui a pour paramètre, la valeur de la tension de collecteur 4,5 V (c'est la valeur en effet qui correspond au point de fonctionnement considéré).

Si l'on augmente le courant de base de 50µA à 70µA, le point C vient en C' comme indiqué sur la figure 3. La tension V_BE augmentera de 162mV à 177mV. La valeur de r_e relative au point de fonctionnement C sera alors :

r_e = (accroissement de V_BE)/(accroissement de I_B ) = (177-162)/(70-50 ) = (15mV)/(20µA) = 0,75kΩ

D'une façon analogue on peut déterminer la résistance dynamique de sortie en opérant sur les caractéristiques de collecteur. Supposons que l'on augmente la tension du collecteur de 4,5 V à 6,5 V en maintenant constante la valeur du courant de base : le point A se déplace en A' et reste encore sur la caractéristique de paramètre I_B = 50µA (figure 4).

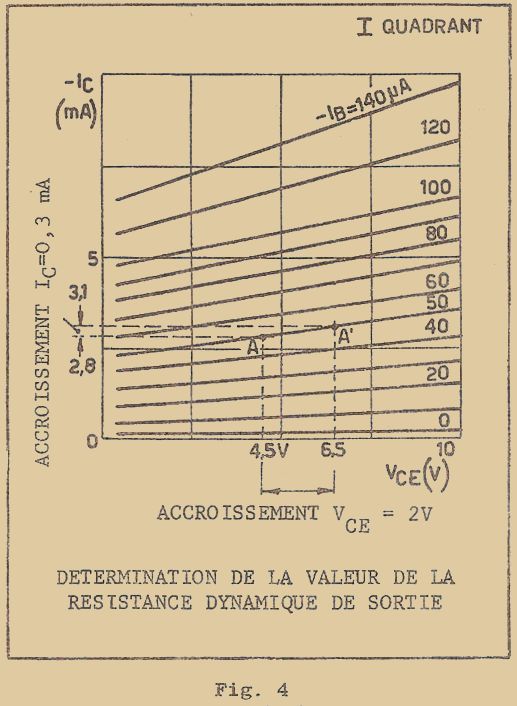
En conséquence d'une telle augmentation de V_CE, le courant de collecteur passe de 2,8mA à 3,1mA comme on peut le voir sur la figure 4.

On a donc :

r_s = (accroissement de V_CE)/(accroissement de I_C ) = (6,5-4,5)/(3,1-2,8 ) = (2 V)/(0,3mA) = 6,67kΩ

Comme vous pouvez le vérifier en comparant les résultats obtenus avec ceux de l'exemple précédent, le transistor, pour le même point de fonctionnement, présente des résistances d'entrée et de sortie différentes, en courant continu et en courant alternatif. En particulier, il présente une résistance d'entrée plus grande en courant continu (3kΩ au lieu de 0,75kΩ), tandis que la résistance de sortie est plus faible (toujours en courant continu) : 1,61kΩ au lieu de 6,67kΩ.

De même, pour le montage en base commune, on peut définir une résistance d'entrée et une en sortie. Pour déterminer leur valeur, on opèrera sur les caractéristiques d'entrée, ou celles du collecteur mais relatives au montage en base commune ; on pourra aussi mesurer les accroissements des tensions et des courants d'entrée et de sortie avec un montage base à la masse.

1 – 3 PARAMÈTRES HYBRIDES

Les paramètres "Hybrides" sont au nombre de quatre pour les transistors basse fréquence et généralement indiqués par la lettre "h". Pour les distinguer, on utilise des indices formés de deux chiffres. Ainsi les quatre paramètres sont indiqués de la façon suivante : h₁₁, h₁₂, h₂₁, h₂₂. Ces symboles se lisent "h un-un ; h un-deux ; h deux-un ; h deux-deux".

Les paramètres étant relatifs à un montage donné, on aura une série de ceux-ci pour le montage en base commune, et une pour celle en émetteur commun. Il faut donc encore distinguer à quel montage ils correspondent, pour cela, l'indice est complété par la lettre "b" dans le premier cas et "e" dans le second.

On aura ainsi pour le montage en base commune, les paramètres h_11b, h_12b, h_21b, h_22b, et pour le montage émetteur commun, les paramètres h_11e, h_12e, h_21e, h_22e.

La définition de chacun des paramètres est la même pour les deux montages : le procédé pour les déterminer est le même. Pour simplifier, je vous expliquerai en détail, le montage émetteur commun seulement.

Considérons encore le schéma de la figure 1, et supposons que le transistor travaille au point de fonctionnement désiré après avoir réglé convenablement R_B et P_C. Nous voulons déterminer les valeurs des paramètres hybrides pour ce point.

Faisons subir à I_B une légère augmentation en maintenant constante la valeur de la tension du collecteur (en retouchant P_C si nécessaire) et appelons i₁ la valeur de cet accroissement. Par analogie, appelons v₁ la valeur correspondante de l'accroissement de la tension de base et i₂ l'accroissement du courant de collecteur. Ces accroissements sont indiqués sur le schéma de la figure 5.

Les paramètres h_11e et h_21e sont définis par les formules suivantes :

h_11e = v₁/i₁ et h_21e = i₂/i₁

On peut ainsi voir ce qu'indiquent ces paramètres, ou comme on dit, quelle est leur signification physique. Ainsi, le paramètre h_11e n'est autre que la résistance d'entrée en courant alternatif. En effet, sa valeur est donnée par le rapport entre l'accroissement de V_BE et l'accroissement de I_B, c'est-à-dire qu'il est défini exactement comme l'était la résistance d'entrée dans le paragraphe précédent. La valeur de h_11e est donc donnée en Ω (ou en kΩ) et est exprimée par la même unité de mesure que la résistance.

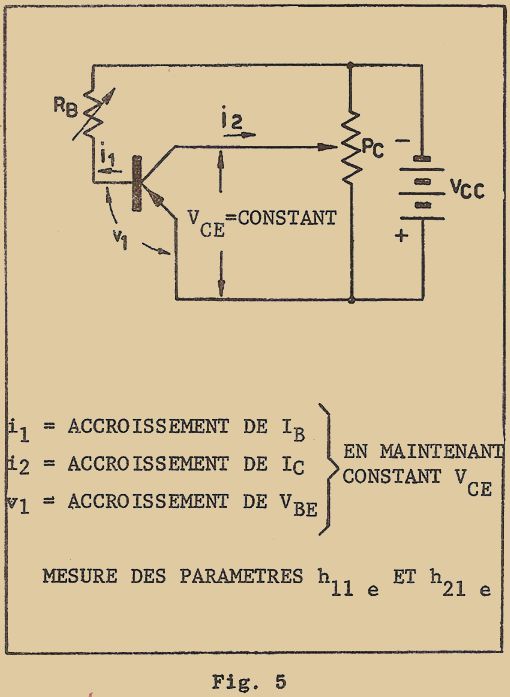
Prenons le paramètre h_21e. Il exprime le rapport de l'accroissement du courant de collecteur à l'accroissement du courant de base. Il exprime donc de combien de fois l'accroissement de I_C est plus grand que l'accroissement correspondant de I_B qui l'a provoqué. Mais si nous nous rappelons la définition du coefficient d'amplification de courant, nous voyons tout de suite que h_21e n'est autre que le coefficient β.

Pour déterminer les deux autres paramètres hybrides, considérons une fois de plus le schéma de la figure 1 et provoquons un accroissement de la tension du collecteur en agissant sur P_C et retouchons R_B pour revenir à la valeur de I_B de départ. Appelons encore v₂, i₂ et v₁, les accroissements respectifs de la tension du collecteur, du courant de collecteur et de la tension de base, comme indiqué sur la figure 6.

Les valeurs de h_22e et de h_12e sont données par les formules :

h_22e = i₂/v₂  et  h_12e = v₁/v₂

La signification physique de ces paramètres est immédiate. Le paramètre h_22e est donné par le rapport de l'accroissement du courant de collecteur à l'accroissement de la tension du collecteur c'est-à-dire qu'il est défini exactement, mais de façon inverse, comme était définie auparavant la résistance de sortie en courant alternatif.

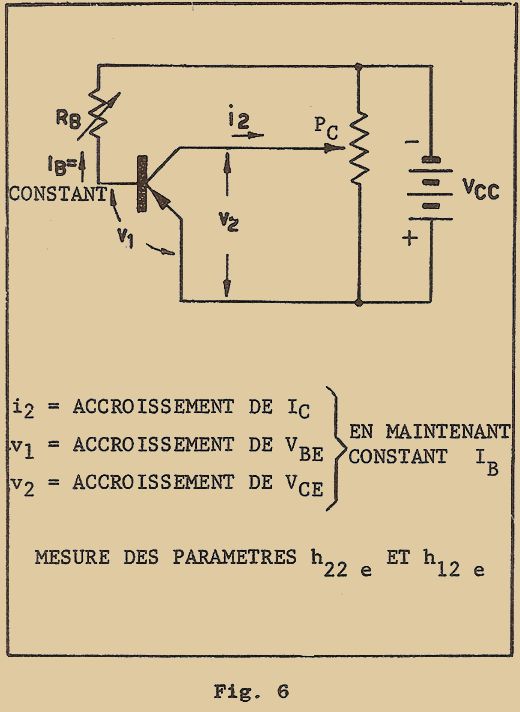
Étant donné que l'inverse d'une résistance est une conductance le paramètre h_22e exprime donc la conductance de sortie du transistor en courant alternatif. Sa valeur peut donc être exprimée en unité de conductance, c'est-à-dire en Siemens (S) ou en millisiemens (mS) ou en microsiemens (µS) ; elle peut aussi être exprimée en mho (mot inverse du mot ohm), mais peut aussi être donnée en mA/V (c'est-à-dire en milliampère par volt, unité tout à fait équivalente au millisiemens) ou en µA/V (équivalente à µS).

Enfin, le paramètre h_12e est donné par le rapport de l'accroissement de la tension de base à l'accroissement de la tension de collecteur qui l'a provoqué. Il indique donc de combien de fois l'accroissement de V_BE est plus grand que l'accroissement de V_CE. Le paramètre est appelé "coefficient de réaction de tension" puisqu'il exprime l'influence de la tension de sortie sur la tension d'entrée.

En général, la tension d'entrée est peu influencée par la tension de sortie et ainsi l'accroissement de V_BE est toujours beaucoup plus faible que l'accroissement de V_CE. Ceci signifie que h_12e est toujours très petit, de l'ordre de quelques millièmes ou même moins.

Si l'on reprend le même raisonnement avec un circuit en base commune, on peut définir les paramètres hybrides h_11b, h_21b, h_12b, h_22b et trouver qu'en particulier h_21b est équivalent au coefficient α.

En conclusion, nous appellerons :

h₁₁ = résistance d'entrée
h₂₁ = coefficient d'amplification en courant
h₁₂ = coefficient de réaction de tension
h₂₂ = conductance de sortie

D'autre part, il faut se rappeler que les deux premiers paramètres doivent être mesurés en maintenant constante la tension de sortie tandis que les deux autres seront mesurées en maintenant constant le courant d'entrée.

Les valeurs ainsi obtenues sont valables uniquement pour le point de fonctionnement considéré, à partir duquel on a fait les accroissements de tension et de courant.

On peut remarquer encore que le nom "hybride" donné à ces paramètres dérive du fait que ceux-ci ne sont pas homogènes en ce qui concerne leurs unités de mesure. En effet, tandis que deux de ceux-ci (h_12et h₂₁) sont donnés par des nombres purs (on dit "sans dimension") le premier (h₁₁) est exprimé en unités de résistance et le dernier (h₂₂) en unités de conductance.

En observant les formules qui définissent les différents paramètres hybrides on peut enfin remarquer que le nombre utilisé en indice pour les distinguer apparemment mystérieux, est en réalité formé par les nombres qui indiquent respectivement les grandeurs qui se trouvent au-dessus (numérateur) et en dessous (dénominateur) de la barre de fraction.

Comme le nombre 1 se réfère à l'entrée et 2 à la sortie, h₁₁ signifie que l'on traitre du paramètre obtenu comme étant le rapport entre deux grandeurs d'entrée. Par analogie, h₂₁, h₁₂, h₂₂ indiquent les paramètres obtenus comme étant le rapport respectivement entre une grandeur de sortie et une d'entrée, entre une d'entrée et une de sortie et enfin entre deux grandeurs de sortie.

Quelquefois, les paramètres sont distingués par d'autres indices. h_11est indiqué par hi en ce sens qu'il représente la résistance d'entrée ("i" étant la première lettre de "input", terme anglais signifiant "entrée"). h_21est indiqué par hf en ce sens qu'il représente l'amplification que l'on a dans le sens "direct", c'est-à-dire l'amplification que subit un courant en passant de l'entrée à la sortie ("f" étant le commencement de "forward" = "direct"). h_12est indiqué par hr, car il exprime une réaction dans le sens "inverse", c'est-à-dire qui se manifeste entre la tension de sortie et celle d'entrée ("r" étant le début de "reverse" = "inverse"). h₂₂ est indiqué par ho en ce sens qu'il indique une conductance de "sortie" ("o" étant le début de "output" = "sortie").

A tension de sortie constante	h11 = résistance d'entrée	hi : input
	h21 = coefficient d'amplification de courant	hf : foward
A courant d'entrée constant	h12 = coefficient de réaction de tension	hr : reverse
	h22 = conductance de sortie	ho : output

1 – 4 VALEURS DES PARAMÈTRES HYBRIDES ET LEUR VARIATION EN FONCTION DU POINT DE FONCTIONNEMENT

Les propriétés d'un transistor dépendent de façon plus ou moins marquée du point de fonctionnement de celui-ci ; on peut donc prévoir que les paramètres hybrides eux aussi vont dépendre du point de fonctionnement, c'est-à-dire qu'ils vont varier lorsque celui-ci va se déplacer.

Pour cette raison, lorsque l'on donne les valeurs des paramètres hybrides il faut toujours bien préciser à quel point de fonctionnement ils se réfèrent. Ainsi par exemple, lorsque le constructeur donne les caractéristiques d'un transistor, il a toujours soin de préciser le point de fonctionnement pour lequel celles-ci ont été relevées, et indique s'il s'agit d'un montage en émetteur commun ou en base à la masse.

Exemple

Montage en émetteur commun	Montage en base commune
h11e = 0,8kΩ	h11b = 17Ω
h21e = β = 47	h21b = α = 0,979
h12e = 0,00054	h12b = 0,0008
h22e = 80µA/V	h22b = 1,6µA/V

A la lecture de ces valeurs, on peut remarquer tout de suite l'énorme différence dans les résistances d'entrée et le coefficient d'amplification de courant lorsque l'on passe d'un montage à l'autre.

D'autre part on remarquera que la conductance de sortie est plus grande dans le montage en émetteur commun, ce qui signifie que la résistance de sortie est plus faible (12,5kΩ correspondant à 80µA/V, contre 625kΩ correspondant à 1,6µA/V).

En effet :

1/(80 x 10^-6) = 10⁶/80 = 12.500Ω = 12,5kΩ

et

1/(1,6 x 10^-6) = 10⁶/1,6 = 625.000Ω = 625kΩ

Dans les deux cas par contre on a une valeur très faible de h₁₂ ; ainsi par exemple pour le montage en émetteur commun, on a h_12e  = 0,00054 ce qui signifie qu'un accroissement de la tension du collecteur de 1 V provoque un accroissement de la tension de base de 0,00054 V soit de 0,54mV seulement.

Pour avoir les valeurs des paramètres hybrides relatifs à d'autres points de fonctionnement, il faut faire appel à des diagrammes que l'on trouve dans les catalogues de transistors. Ces diagrammes sont relatifs au type de transistor considéré et ne sont donnés en général que pour le montage en émetteur commun, car le plus utilisé en pratique.

L'exemple d'un tel graphique est donné à la figure 7. Les deux graphiques de la figure 7 sont relatifs à un transistor basse fréquence de moyenne puissance et servent à passer du point de fonctionnement V_CE = 2 V et I_C = 3mA à un point quelconque dans le champ des possibilités d'un tel transistor.

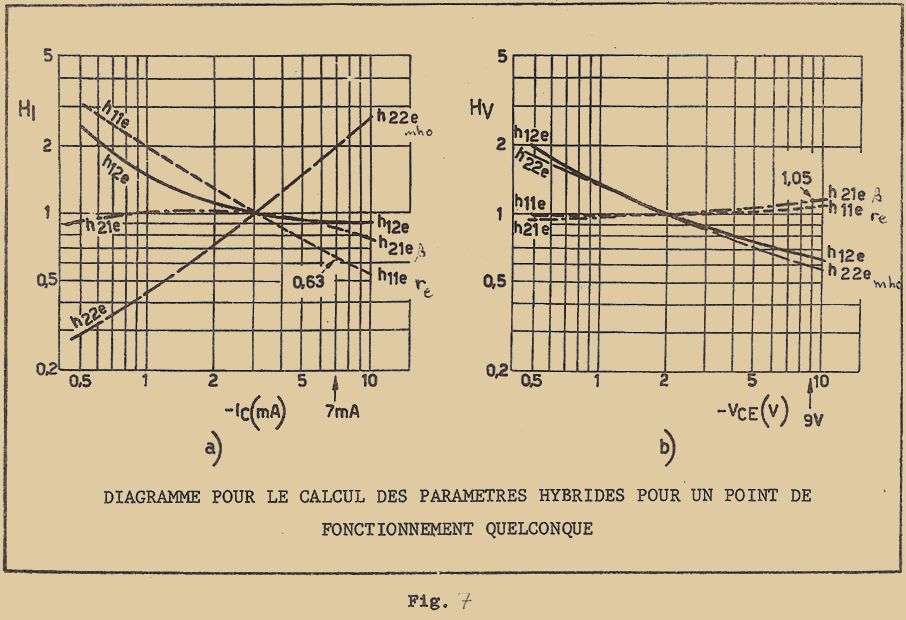
Le diagramme de la figure 7-a tient compte du courant I_C du nouveau point de fonctionnement, tandis que la figure 7-b tient compte de la tension V_CE.

On désire par exemple calculer les paramètres hybrides pour le point de fonctionnement V_CE = 9V, I_C = 7mA. On cherche alors sur la figure 7-a, la valeur I_C = 7mA et on lit sur l'échelle verticale en correspondance de la courbe h_11e, la valeur H_I = 0,63. Sur la figure 7-b, en correspondance de la valeur 9V lue sur l'échelle horizontale, on lit sur l'échelle verticale, toujours pour la courbe h_11e, la valeur H_V = 1,05.

La valeur h'_11e, relative au nouveau point de fonctionnement, sera donnée par la formule suivante où h_11e est la valeur relative au point de fonctionnement de départ :

h'_11e = h_11e x H_V x H_I = 0,8 x 0,63 x 1,05 = 0,8 x 0,662 = 0,53kΩ

En procédant de la même façon pour les autres paramètres, on trouve :

pour h_21e :

H_I = 0,85 ; H_V = 1,1 d'où h'_21e = h_21e x 0,85 x 1,1 = 47 x 0,935 = 44 environ

pour h_12e :

H_I = 0,9 ; H_V = 0,64 d'où h'_12e = h_12e x 0,9 x 0,64 = 0,00054 x 0,576 = 0,00031 environ

pour h_22e :

H_I = 2 ; H_V = 0,6 d'où h'22 e = h_22e x 2 x 0,6 = 80 x 1,2 = 96µA/V.

Vous pouvez voir à l'aide de ces diagrammes, comment évoluent en général les paramètres hybrides relatifs au montage en émetteur commun. L'allure de ces courbes est générale pour les transistors BF de faible puissance.

En observant le diagramme de la figure 7-a, on peut constater que la résistance d'entrée h_11e du transistor diminue très rapidement lorsque I_C croît. La conductance de sortie h_22e croît au contraire très rapidement, mais comme la conductance est l'inverse d'une résistance, on en déduit que la résistance de sortie diminue elle aussi notablement, lorsque le courant de collecteur augmente.

Le coefficient d'amplificateur β (h_21e) reste au contraire, pratiquement constant.

Par analogie si l'on observe le diagramme de la figure 7-b, on voit que la résistance d'entrée et le coefficient β restent sensiblement constants lorsque la tension de collecteur augmente, tandis que la conductance de sortie diminue légèrement, ce qui signifie que la résistance de sortie augmente un peu.

1 – 5 INFLUENCE DE LA TEMPÉRATURE SUR LES PARAMÈTRES HYBRIDES

Les paramètres hybrides, comme les caractéristiques d'un transistor, varient en fonction de la température à laquelle se trouve soumis le transistor, ou mieux en fonction de la température de sa jonction. Les valeurs indiquées sur les catalogues, se réfèrent en général à une température de 25°C (ou celle indiquée).

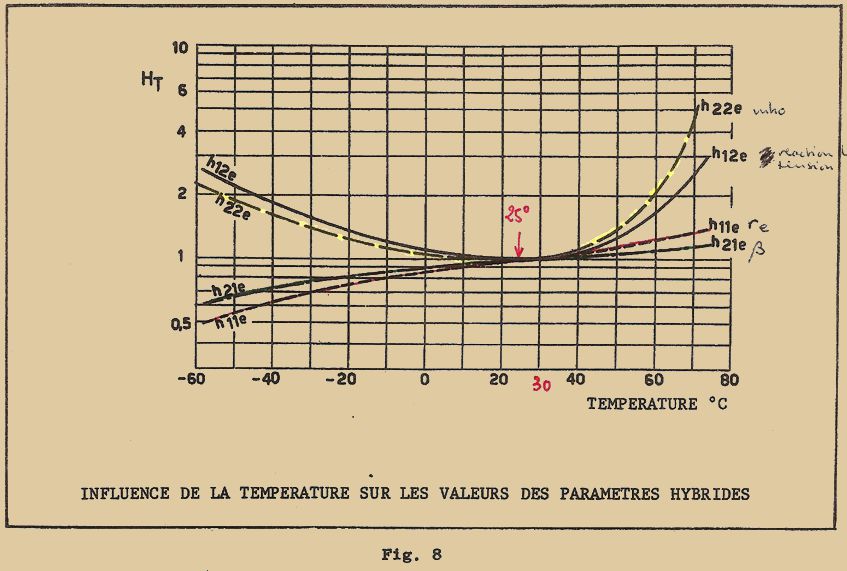
Je vous ai reporté à la figure 8 un diagramme du type de celui de la figure 7, qui donne le coefficient HT. C'est par la valeur de ce coefficient HT qu'il faut multiplier les valeurs des paramètres hybrides, relatifs à 25°C, pour obtenir celles relatives à une température comprise entre – 60°C et + 80°C. Un tel diagramme est relatif à un transistor basse fréquence de faible puissance.

Vous pouvez voir sur la figure 8 qu'avec l'augmentation de la température au-dessus de 25°C, tous les paramètres croissent, mais tandis que la résistance d'entrée et le coefficient d'amplification augmentent peu, la conductance de sortie et le coefficient de réaction augmentent beaucoup.

Ainsi par exemple si l'on passe de 25°C à 70°C, la conductance de sortie devient quatre fois et demie plus grande, c'est-à-dire qu'elle passe de 80µA/V à 360µA/V, ce qui signifie que la résistance de sortie devient quatre fois et demie plus petite. Pour le même accroissement de température, le coefficient β augmente seulement de 1,1 environ, c'est-à-dire qu'il passe de 47 à 52 environ

Par contre si la température diminue en dessous de 25°C, la résistance d'entrée et le coefficient d'amplification diminue graduellement, tandis que la conductance de sortie et le coefficient de réaction recommencent à grimper. Ainsi par exemple, pour une température de – 25°C, h_21e diminue de 0,78 fois environ, c'est-à-dire qu'il passe de 47 à 36,6.

1 – 6 DÉTERMINATION DES PARAMÈTRES HYBRIDES SUR LES COURBES CARACTÉRISTIQUES

La valeur des paramètres hybrides des détermine en opérant sur les courbes caractéristiques du transistor, considérant évidemment le point de fonctionnement qui nous intéresse.

Pour déterminer le paramètre h_11e, vous devez procéder comme il a été indiqué sur la figure 3, car comme nous l'avons vu précédemment, ce paramètre correspond à la résistance d'entrée du transistor en courant alternatif.

Pour déterminer le paramètre h_22e, vous procéderez comme il a été indiqué à la figure 4, sauf que maintenant, il faudra faire le rapport entre l'accroissement du courant et celui de la tension de collecteur, car ce paramètre correspond à l'inverse de la résistance de sortie.

Pour déterminer le paramètre h_21e, vous pourrez opérer sur les courbes caractéristiques du collecteur suivant la définition même de ce paramètre. Il faudra déterminer l'accroissement du courant de collecteur provoqué par un accroissement du courant de base, quand la tension de collecteur reste constante.

Considérons le point de fonctionnement déjà fixé précédemment, c'est-à-dire le point A sur la figure 9. Déplaçons ce point vers le haut sur une droite verticale, de façon à ce que la tension de collecteur reste toujours la même et égale par exemple à 4,5 V. Si nous passons de la caractéristique 50µA à celle de 70µA, c'est-à-dire si le point s'est déplacé de A en A', nous aurons obtenu un accroissement du courant de base de 70 – 50 = 20µA et telle sera la valeur de i₁ dans la formule définissant h_21e.

L'accroissement correspondant de I_C sera la différence entre les valeurs du courant de collecteur lues sur l'échelle verticale pour les points A' et A. Nous aurons donc :

i₂ = 4 – 2,8 = 1,2mA = 1.200µA

La valeur de h_21e est alors immédiate, nous rappelant que les valeurs des deux courants doivent être exprimées toutes les deux dans les mêmes unités,

h_21e = 1.200/20 = 60

Si le point de fonctionnement considéré tombe entre deux caractéristiques, comme par exemple le point F de la figure 9, il n'est pas nécessaire de procéder à des opérations compliquées d'interpolation, mais il suffit de considérer deux points, un au-dessus et l'autre en-dessous de F qui tombent sur deux caractéristiques différentes. Ainsi, il suffira de prendre par exemple les points F' et F'' et d'opérer comme précédemment.

Il faut encore remarquer, qu'en passant d'une caractéristique à celle située immédiatement au-dessus, l'augmentation de I_B (c'est-à-dire i₁) est toujours la même (par exemple dans le cas de la figure 9, i₁ = 10µA) car les caractéristiques de I_B différant toutes de 10µA, tandis que l'accroissement correspondant de I_C (c'est-à-dire i₂) sera d'autant plus grand que les caractéristiques seront plus éloignées entr'elles.

Ceci signifie donc que plus les caractéristiques seront éloignées, plus grande sera la valeur de h_21e puisque la valeur de i₂ sea plus élevée, i₁ restant toujours le même.

Si donc, l'on observe les courbes de la figure 9, on constate qu'en déplaçant le point de fonctionnement vers la droite (ce qui équivaut à augmenter la tension de collecteur), les caractéristiques s'allongent : h_21e augmente ce qui est en accord avec les résultats du diagramme de la figure 7-b, pour la courbe relative à h_21e.

Il nous reste encore à déterminer le paramètre h_12e. A ce propos il faut tout de suite noter que ce paramètre est assez mal déterminé à cause de sa valeur extrêmement faible. Considérant en effet le point de fonctionnement D (sur les caractéristiques mutuelles de tension de la figure 2), il y a lieu de provoquer un accroissement de la tension de collecteur (en maintenant le courant de base constant) et de déterminer l'accroissement correspondant de la tension de base.

Ceci signifie donc qu'il faut déplacer le point de fonctionnement D sur la caractéristique 50µA, en l'amenant par exemple au point D' (figure 10) : l'accroissement de V_CE, c'est-à-dire v₂, est alors de 2 volts.

L'accroissement correspondant de V_BE, c'est-à-dire v₁, doit être déterminé en lisant sur l'échelle verticale les valeurs de la tension de base respectivement aux points D et D'.

Étant donné que les caractéristiques mutuelles de tension, pour le montage en émetteur commun, sont pratiquement des droites horizontales, comme on peut le voir sur la figure 10, il est donc très difficile, sinon impossible d'évaluer l'accroissement de V_BE.

2 PARAMÈTRES RÉSISTANTS (OU "r")

D'autres paramètres sont parfois utilisés pour les transistors de basse fréquence et de faible puissance : on les appelle paramètres résistants ou "r". Cette dénomination provient du fait, qu'ils sont tous exprimés en unités de résistances, c'est-à-dire en ohms ou en kΩ.

Ce système est constitué de trois paramètres résistants proprement dits et du coefficient α. Ils sont représentés par le symbole r_e, r_b et r_c et indiquent les valeurs des résistances internes du transistor que présentent séparément l'émetteur, la base et le collecteur. Comme une telle séparation des trois résistances internes n'est pas possible du point de vue physique, on voit tout de suite que les paramètres "r" ne peuvent être mesurés en pratique. Leur emploi ne se justifie en premier lieu que par une certaine simplification des calculs.

L'avantage essentiel est purement du point de vue calculs, car avec ces paramètres on obtient des formules plus simples pour établir le projet d'un amplificateur ou d'un circuit quelconque.

Un autre avantage est qu'ils ne changent pas de valeur lorsque l'on passe d'un montage en émetteur commun à celui en base à la masse, comme cela arrivait avec les paramètres hybrides.

Les formules qui permettent de calculer les paramètres "r" en partant des paramètres hybrides relatifs au montage en base commune, sont indiqués ci-dessous :

Si nous remplaçons dans ces formules, les valeurs des paramètres hybrides que nous avons vus jusqu'ici, nous obtenons les valeurs des paramètres "r" relatifs au même point de fonctionnement déjà considéré à savoir V_CE = 2 V – I_C = 3mA.

Si nous exprimons h_11b en Ω et h_22b en µA/V, nous obtenons r_b et r_e en Ω, tandis que r_c est exprimé en kΩ.

r_b = (1.000.000 x h_12b)/h_22b  = (1.000.000 x 0,0008)/1,6 = 800/1,6 = 500Ω

r_e = h_11b – r_b x (1 – α) = 17 – 500 x (1 - 0,979) = 17 – 500 x 0,021 = 17 – 10,5 = 6,5Ω

r_c = 1.000/h_22b  = 1.000/1,6 = 625kΩ

Quelquefois dans les catalogues, on ne trouve que les valeurs des paramètres "r" et le coefficient α, tandis que l'on désirerait connaître les valeurs des paramètres hybrides relatifs au montage en base commune, ou en émetteur commun.

On peut calculer ces valeurs par les formules que je vous donne ci-dessous où l'on doit exprimer r_b et r_e en Ω et r_c en kΩ.

De cette manière, les paramètres h_11b et h_11e seront exprimés en Ω et les paramètres h_22b et h_22e en µA/V.

Pour le montage en base commune, on aura :

h_11b = r_e + r_b x (1 – α)
h_21b = α
h_12b = r_b/(1.000 x r_c )
h_22b = 1.000/r_c

Pour le montage en émetteur commun, on aura :

h_11e = r_b + r_e/(1- α)
h_21e = α/(1- α)
h_12e = r_e/(r_c x (1- α) x 1.000)
h_22e = 1.000/(r_c x (1- α))

3 – PARAMÈTRES DES TRANSISTORS POUR LES FRÉQUENCES ÉLEVÉES

Les quatre paramètres que nous avons vus jusqu'ici, ne sont pas suffisants pour déterminer complètement les propriétés d'un transistor lorsque la fréquence est élevée, c'est-à-dire pour les fréquences radio ou celles qui sont utilisées dans les étages changeurs de fréquence, ou de fréquence intermédiaire des récepteurs.

On ne peut absolument pas dans ce cas, négliger par exemple la capacité des jonctions qui, quoique de valeur relativement faible, présente aux fréquences élevées, une réactance assez basse modifiant les résistances d'entrée et de sortie du transistor.

Ainsi, il devient évident, qu'il faudra tenir compte de la capacité des jonctions, ou des capacités équivalentes, ce qui va porter à 6, le nombre total de paramètres.

Comme vous pouvez le voir sur la figure 11, dans le montage en base commune, la capacité d'entrée coïncide avec la capacité de la jonction émetteur-base, et celle de sortie avec la capacité de la jonction collecteur-base. Nous avons déjà parlé de ces capacités au moment où nous avons étudié les jonctions.

Etant donné la complexité du problème et la non homogénéité des paramètres selon les différents fabricants de transistors, nous n'entreprendrons leur étude que plus tard, au moment où nous arriverons aux circuits travaillant en H.F.

---

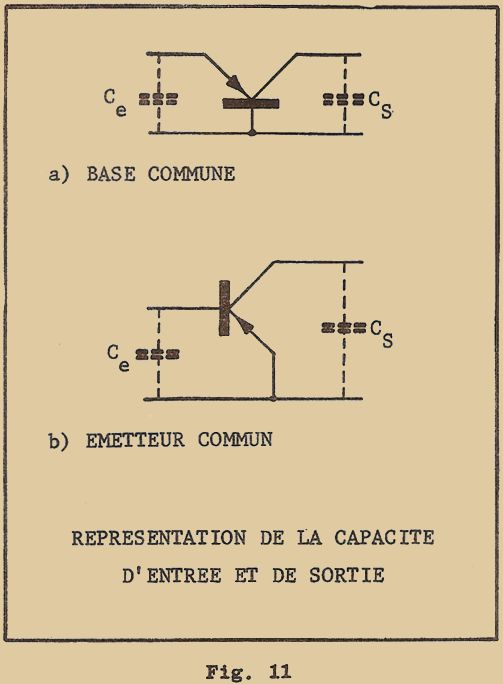
RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 11^ème LEÇON THÉORIQUE

1 – Parce qu'il se comporte comme le courant inverse d'une diode à jonction.

2 – La valeur de I_CBo se trouve approximativement doublée chaque fois que la température augmente de 10°C.

3 – C'est dans le montage en émetteur commun, que le courant de collecteur est le plus influencé par la température.

4 – L'élévation de la température, provoque un déplacement vers le haut des courbes caractéristiques de collecteur et un espacement plus grand entre celles-ci.

5 – Le coefficient de stabilité S est défini comme le quotient entre l'accroissement de I_C relatif à une augmentation donnée de la température et l'accroissement correspondant de I_CBo.

6 – Pour le montage en base commune, on a toujours S = 1, tandis qu'en émetteur commun on a S = (β + 1).

7 – Avoir S égal par exemple à 10, signifie que pour une augmentation donnée de la température du transistor, l'augmentation du courant I_C sera dix fois plus grande que celle de I_CBo.

8 – Pour réduire l'augmentation du courant de collecteur provoquée par la température, on monte des circuits particuliers de polarisation qui utilisent la contre-réaction de collecteur et d'émetteur en réduisant de façon opportune le courant de base.

9 – Il est nécessaire de stabiliser du point de vue thermique, le point de fonctionnement d'un transistor, pour éviter que celui-ci n'atteigne la zone de saturation ou, pire encore, la zone où la dissipation du collecteur serait excessive.

---

EXERCICES DE RÉVISION SUR LA 12^ème LEÇON THÉORIQUE

1 – Quelle est la différence entre la résistance statique et la résistance dynamique ?

2 – Combien y a-t-il de paramètres hybrides ?

3 – Quelle est la signification physique des paramètres hybrides ?

4 – En quelles unités de mesure, sont donnés les paramètres hybrides ?

5 – Que doit-on toujours bien spécifier, lorsque l'on donne la valeur de ces paramètres ?

6 – Comment peut-on obtenir la valeur des paramètres hybrides ?

7 – Comment varient les paramètres hybrides, quand la température du transistor s'élève au-dessus de la température ambiante ?

8 – Peut-on mesurer pratiquement les paramètres "r" ?

9 – Quels sont les avantages des paramètres "r" par rapport aux paramètres hybrides ?

Fin de la leçon 12

---

LECON 13

TECHNOLOGIE DES SEMI-CONDUCTEURS

Dans les leçons précédentes, nous avons vu comment fonctionnait un transistor, dans quelles conditions il travaillait, et quelles en étaient les limites. Avec les notions qui ont été définies, il suffit de respecter les données du constructeur pour utiliser correctement les diodes et les transistors, et on peut ne pas se préoccuper du mode de fabrication de ceux-ci.

Mais il me semble qu'il est quand même très utile de connaître quelques notions de technologie afin de mieux comprendre certaines limites de fonctionnement, et savoir pourquoi, lorsque l'on doit établir le projet d'un circuit à transistors, il faut respecter les données particulières.

Les caractéristiques que nous avons examinées dépendent d'une façon générale des propriétés des semi-conducteurs ; mais en pratique la possibilité d'obtenir des semi-conducteurs qui auront des propriétés désirées est liée d'une manière déterminante, aux traitements physiques et chimiques des matériaux ainsi qu'aux précautions qui seront prises pendant les différentes phases mécaniques.

Ainsi, par exemple, la tension inverse maximum des diodes est déterminée par la résistivité des semi-conducteurs utilisés, c'est-à-dire fonction du degré de pureté des matériaux ; la fréquence de coupure des transistors est dûe, comme nous le verrons dans les prochaines leçons, au temps de transit des charges électriques, et la durée de ce temps dépend des dimensions géométriques de la base et de la distribution des impuretés dans la jonction ; la puissance que les diodes et les transistors peuvent supporter est liée directement à leurs dimensions ; la durée de vie des circuits réalisés dépendra donc du soin que l'on aura pris dans l'établissement du projet de ce montage.

Dans cette leçon nous étudierons la technique adoptée dans la fabrication du germanium et du silicium, qui sont les éléments les plus largement utilisés dans la production des dispositifs à semi-conducteurs ; nous examinerons ensuite, les opérations fondamentales de coupe des monocristaux et réserverons pour la prochaine leçon, l'étude de la technique de montage des diodes et des transistors.

1 – EXTRACTION ET RAFFINAGE DU GERMANIUM

1 – 1 FONTE

On trouve dans la nature, le germanium mélangé à d'autres éléments, à l'état de sel, mais jamais à l'état de métal pur.

On calcule que la croûte terrestre contient en moyenne 7 grammes de germanium par tonne, c'est-à-dire environ sept parties pour un million.

La quantité globale de germanium est beaucoup plus faible que celle du silicium qui est contenu dans la proportion de 277.200 parties pour un million, c'est-à-dire qu'il présente environ le ¼ du poids total de l'écorce terrestre.

D'autre part, la quantité du germanium est environ 14 fois supérieure à celle du mercure qui n'est pas considéré comme métal rare, et n'est pas non plus très inférieure à celle du plomb, métal très largement utilisé depuis l'antiquité. Toutefois, les minerais de germanium sont très éparpillés et il est difficile d'organiser une exploitation économique des gisements.

La Germanite qui est un sel de soufre de germanium et de cuivre, se trouve en abondance en Afrique du Sud occidentale seulement : l'Argirodite, sulfure de germanium et d'argent et l'Ultrabasite, sulfure de germanium, d'antimoine, de plomb et d'argent, sont dispersés dans des roches qui contiennent surtout d'autres minerais. On préfère donc extraire le germanium nécessaire aux industries des semi-conducteurs, par fonte des minerais que je viens de vous citer, peut-être moins riches, mais plus économiques.

Ainsi tout le germanium nécessaire aux besoins de l'électronique est tiré ses sous-produits des industries du carbone, du zinc et du cadmium. Les suies de certains carbone, les scories du zinc et du cadmium, peuvent contenir du germanium à l'état de bioxyde, c'est-à-dire combiné à de l'oxygène dans la proportion de un atome de germanium pour deux atomes d'oxygène.

Les différents procédés d'extraction du bioxyde des sous-produits cités ne sont pas très différents les uns des autres et donnent des pourcentages de germanium (environ 1%) à peu près équivalents ; ils peuvent donc être considérés comme également avantageux.

Les industries des Etats-Unis et de la Russie procèdent surtout à partir des suies de carbone, tandis que celles des pays européens procèdent à partir des blendes (sulfure de zinc).

A la figure 1, je vous ai représenté de façon schématique, les principales transformations chimiques qui ont lieu pendant les différents traitements en vue de l'extraction du bioxyde de germanium à partir des blendes et des suies.

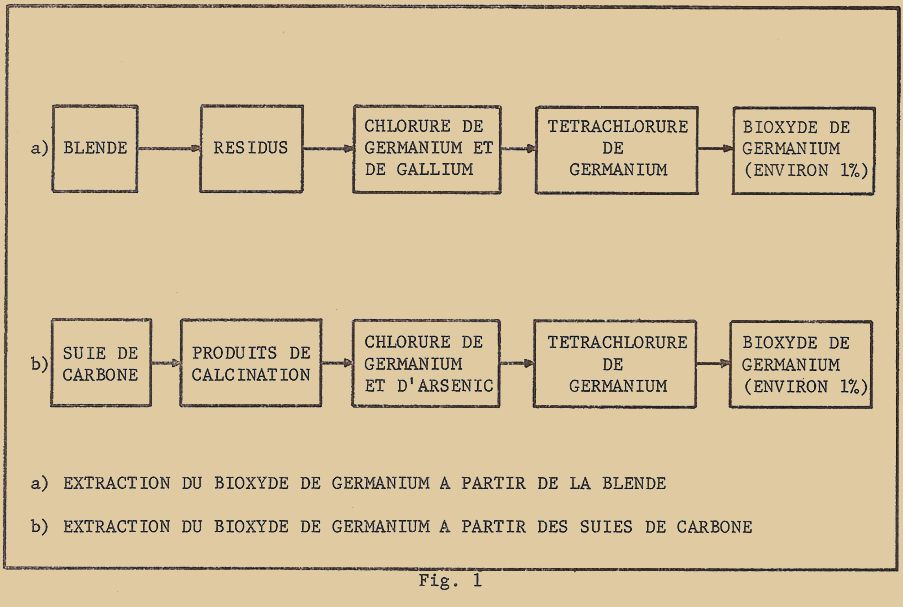
Le bioxyde que l'on obtient est loin de posséder le degré de pureté nécessaire. Il contient de nombreux éléments d'impuretés qu'il faut éliminer par voie chimique avant d'extraire le germanium métallique.

Dans ce but, on transforme le bioxyde en tétrachlorure de germanium ; le tétrachlorure est mis en solution et distillé à plusieurs reprises, jusqu'à ce que les analyses révèlent un degré de pureté suffisant. Ensuite le tétrachlorure est versé dans de l'eau, où se forme par hydrolyse un bioxyde de germanium suffisamment pur.

1 – 2 REDUCTION DU BIOXYDE DE GERMANIUM

L'extraction du germanium métallique à partir du bioxyde se fait par un procédé chimique appelé Réduction.

Dans ce but, on lave le bioxyde avec de l'eau très pure, puis on le dessèche et le pulvérise en des particules minuscules qui prennent une splendide couleur blanche.

Cette poudre est placée dans une coupelle en graphite et introduite dans un four, schématisé à la figure 2.

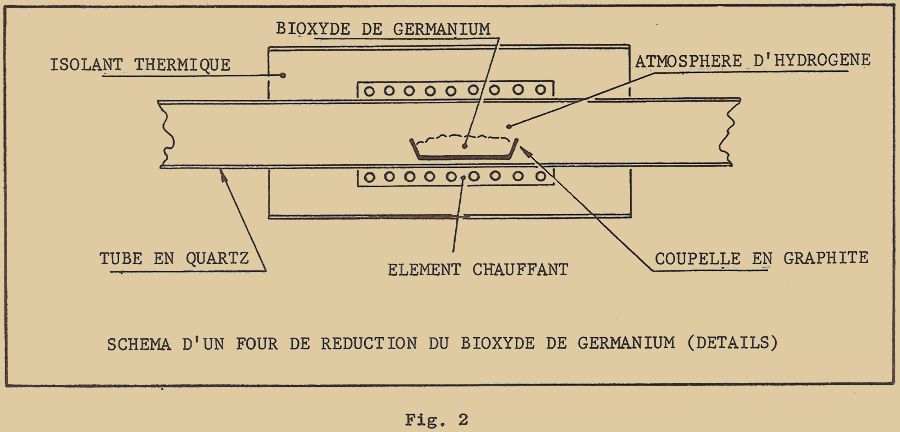
On fait passer dans le tube à quartz un courant d'hydrogène pour qu'il y ait réduction.

Grâce à la résistance chauffante disposée autour du tube, on élève la température du four jusqu'à 650°C environ.

Dans ces conditions, l'hydrogène se combine à un des deux atomes d'oxygène contenus dans la molécule du bioxyde, et il se forme ainsi de l'eau à l'état de vapeur qui est évacuée par le courant d'hydrogène.

Après un certain temps (au minimum deux heures) on recueille dans la coupelle, au lieu du bioxyde, un nouveau composé de germanium : Le monoxyde qui est constitué en quantités égales d'atomes de germanium et d'oxygène, tandis que la proportion était avant de un pour deux.

Pour libérer le germanium métallique, on élève rapidement la température du four jusqu'à 1.000°C et en quelques minutes, les atomes restant d'oxygène se combinent avec l'hydrogène pour former encore de l'eau.

Le germanium, qui à la température de 1.000°C se présente à l'état liquide, est refroidi dans le même four, et à la fin de l'opération, on extrait de la coupelle, un barreau constitué par un aggloméré de petits cristaux, mais qui ne sont pas encore suffisamment purs pour être utilisés dans l'industrie.

1 – 3 RAFFINAGE DU GERMANIUM MÉTALLIQUE

Pour obtenir du germanium à un degré élevé de pureté indispensable pour les opérations suivantes, on introduit le barreau dans un four spécial représenté de façon schématique à la figure 3.

Le four est constitué par un long tube de quartz sur lequel sont placées des bobines reliées entre elles en série.

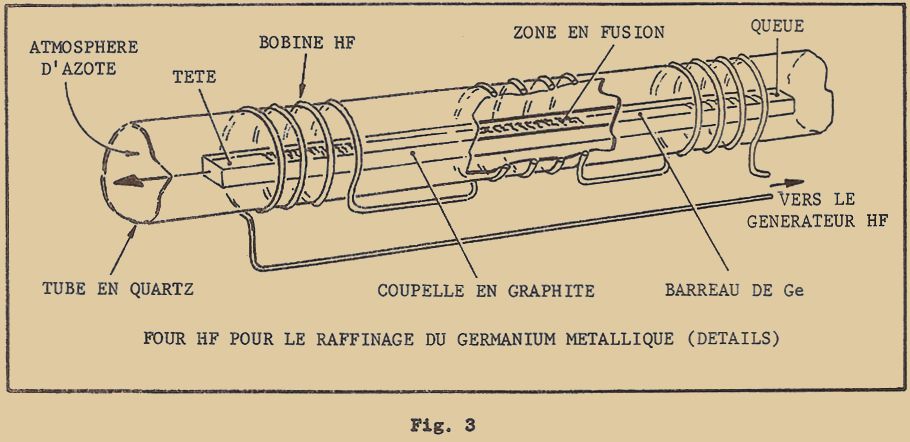
Le circuit de la bobine est alimenté par un générateur de courant à haute fréquence ; on a ainsi à l'intérieur du four, un champ magnétique variable, particulièrement intense sous chaque bobine. Par induction électromagnétique dans la zone du barreau se trouvant sous les bobines, il se forme des courants électriques très intenses qui provoquent une fusion locale du germanium.

La coupelle qui contient le barreau avance lentement d'une extrémité du four à l'autre ; quand la région de la tête du barreau passe sous la première bobine, le germanium est chauffé et fond à cet endroit, tandis que les régions voisines s'échauffent évidemment mais restent encore à l'état solide.

La coupelle avance lentement, et le germanium liquide se solidifie de nouveau, et la première zone de fusion se déplace vers l'autre extrémité du barreau.

Sous la seconde bobine, il se forme une autre zone de fusion qui comme la première va parcourir le barreau de la tête à la queue.

Le processus se renouvelle sous la troisième bobine puis sous toutes les autres, et il se forme ainsi autant de zones de fusion mobiles qu'il y a de bobines placées sur le tube de quartz. Lorsque la dernière zone de fusion a atteint la région de la queue du barreau, c'est-à-dire lorsque la coupelle arrive à la sortie du four, on sait qu'une bonne partie du germanium a atteint le degré de pureté voulu.

Il reste encore à voir comment on obtient le raffinage au moyen de ces zones de fusion mobiles.

1 – 4 PROCESSUS DE FORMATION DE LA ZONE DE FUSION MOBILE

Supposons que le barreau de germanium représenté schématiquement sur la figure 4, se déplace vers S indiqué par la flèche et que les deux frontières F1 et F2 de la zone de fusion se déplacent vers le point opposé s.

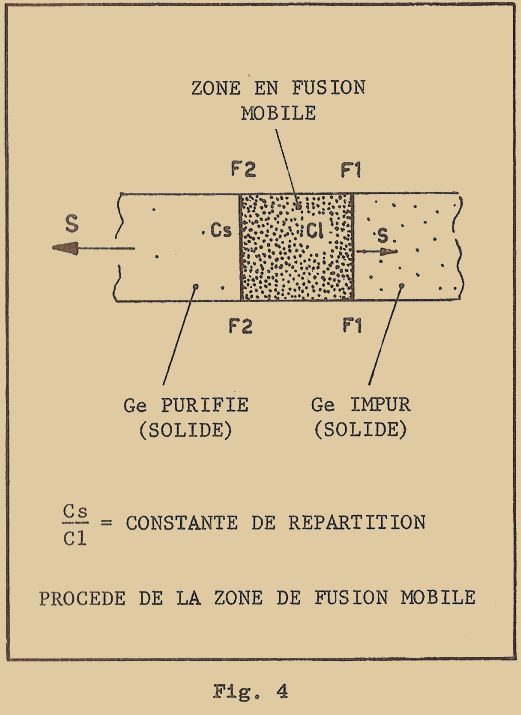
La partie avant F2 peut être comparée à un filtre poreux qui laisse passer le germanium et arrête les impuretés en les maintenant dans la zone de fusion.

C'est ce qui arrive pour les impuretés qui restent libres plus facilement dans un liquide que dans un solide.

Supposons que la concentration des impuretés dans le germanium qui redevient solide après son passage dans la zone de fusion soit C_s et que la concentration des mêmes impuretés dans la zone de fusion (liquide) soit C₁ beaucoup plus grande que C_s.

En faisant le rapport entre les deux concentrations C_s⁄C₁ on trouve par expérience que celui-ci reste constant pendant que la zone de fusion se déplace d'une extrémité à l'autre du barreau.

Ce rapport a une valeur déterminée pour chaque type d'impuretés et pour chaque type de semi-conducteur.

Cette valeur, appelée Coefficient de Répartition (ou Constante d'isolement) des impuretés dans le semi-conducteur peut servir à représenter l'action de raffinage de la partie avant de F2.

Le coefficient de répartition de l'antimoine dans le germanium est égal à 5/1.000 ; ceci exprime donc qu'à gauche de F2, on ne trouvera que cinq parties d'antimoine sur 1.000 parties qui resteront en solution dans la zone de fusion.

Pour le même antimoine, le coefficient de répartition dans le silicium est égal à 40/1.000 : ceci signifie donc qu'à travers F2 passeront 40 atomes d'antimoine sur 1.000 qui resteront dans la zone de fusion.

De ces résultats, nous voyons que l'action de raffinage de F2 sera moins marquée pour le silicium que pour le germanium.

Si nous considérons maintenant un autre type d'impuretés, l'indium par exemple, son coefficient de répartition dans le germanium est égal à 1,2/1.000 ; soit 12/10.000 ; ceci veut dire que 12 atomes d'indium passeront dans le germanium solide, à travers F2, tandis que 10.000 resteront dans la zone de fusion et qu'ainsi l'action de raffinage de F2 est plus marquée pour l'indium que pour l'antimoine.

Pour l'indium réparti dans le silicium, le coefficient de répartition est égal à 0,5/1000 : cinq atomes seulement d'indium resteront dans le silicium solidifié pour 10.000 qui resteront dans la zone de fusion.

Ainsi donc, pour cet élément d'impuretés et avec le procédé de la zone de fusion mobile, on pourra mieux raffiner le silicium que le germanium.

Nous avons vu, que tout le barreau de germanium était successivement parcouru par la zone de fusion. Nous sentons par intuition qu'à l'action de raffinage de la première zone, s'ajoute celle de la seconde puis celle de la troisième, etc… et que nous pouvons obtenir ainsi, un degré de pureté très grand. Avec un tel procédé il ne reste dans le germanium que quelques atomes d'impuretés, c'est-à-dire moins d'un atome sur 10 milliards d'atomes de germanium.

1 – 5 CONTRÔLE DE LA RÉSISTIVITÉ

Avant de passer aux opérations ultérieures il faut s'assurer que le raffinage du germanium est uniforme ; à cet effet, on contrôle la résistivité tout le long du barreau.

Si la résistivité est constante, la distribution des impuretés résiduelles est uniforme.

En pratique, on trouve que la résistivité du barreau est presque constante jusqu'aux deux tiers de la longueur à partir de sa tête, tandis qu'elle diminue rapidement dans le dernier tiers comme on peut le voir sur le graphique de la figure 5.

La diminution de la résistivité est dûe à la présence de toutes les impuretés récoltées et transportées par la zone de fusion mobile.

Après ce contrôle, on coupe la queue et on utilise seulement la partie présentant une résistivité constante.

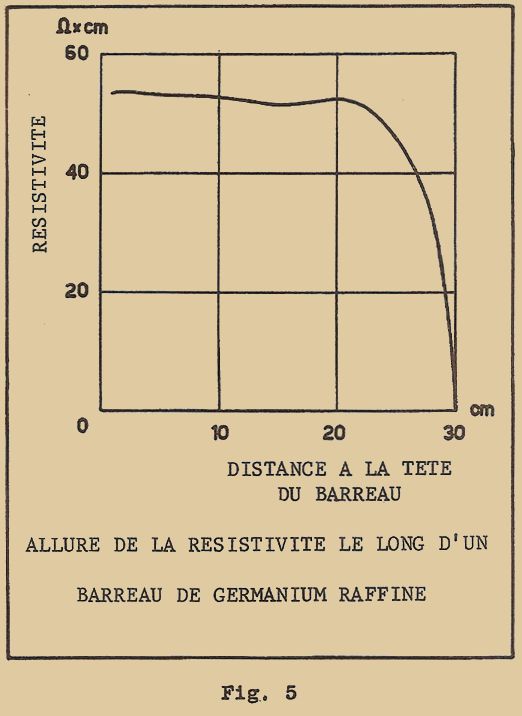
2 – EXTRACTION ET RAFFINAGE DU SILICIUM

Le silicium est très répandu dans la nature sous forme de bioxyde (silice), de sel (silicate) et d'anhydride.

Nous avons déjà vu que cela représentait environ le quart de l'écorce terrestre ; mais il reste encore à préciser que malgré sa grande diffusion et bien que l'on connaisse depuis plus d'un siècle les différents procédés d'extraction du silicium à partir de ces minerais, la production en vue des besoins de l'électronique est sensiblement plus onéreuse que celle du germanium.

En effet avec les procédés classiques de réduction du bioxyde en chauffant les sables à 3.000°C en présence du coke, on obtient du silicium sous forme de polycristaux contenant des impuretés au taux de 2 à 3%. Or pour l'électronique, on doit obtenir du silicium très pur, avec des impuretés de moins de 0,5 ‰.

Les procédés qui permettent d'obtenir le degré de pureté voulu sont très longs et beaucoup plus coûteux que ceux permettant la réduction du bioxyde.

Un certain degré de pureté peut être obtenu en traitant par voie chimique du silicium de fabrication courante à l'aide d'acides chlorhydrique, sulfurique ou fluorhydrique ; mais actuellement, d'autres procédés sont utilisés qui partant d'un sel de silicium (le tétrachlorure) permettent d'obtenir des cristaux de très grande pureté.

Pour le raffinage des cristaux par voie physique, on utilise la méthode de la Zone de suspension qui est une variante de la méthode de la Zone de fusion décrite précédemment.

Le barreau est maintenu fixe, dans une position verticale (figure 6). Une spire mobile, parcourue par un courant à haute fréquence, se déplace lentement le long du tube de quartz et fait avancer le long du barreau la zone de fusion qui se trouve englobée entre deux tranches solides.

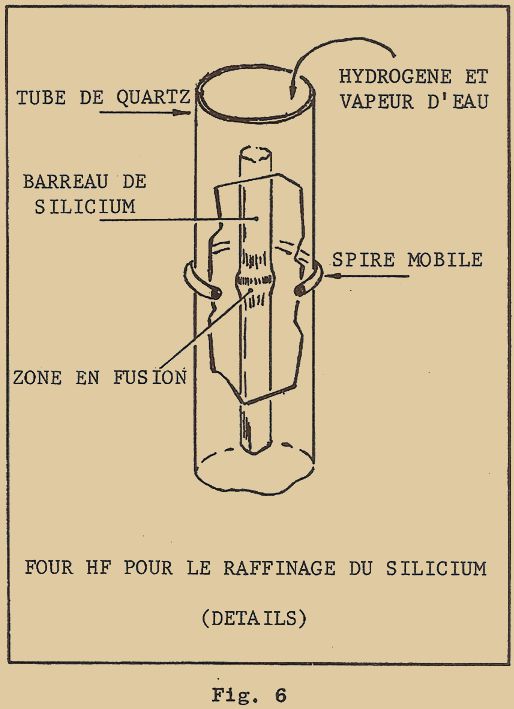
Le procédé est repris à plusieurs reprises d'une extrémité à l'autre du barreau, jusqu'à l'obtention du degré de pureté désiré.

Avec le silicium on ne peut utiliser des fours horizontaux (figure 3) car le silicium en fusion se combinerait avec le matériau de la coupelle et il y aurait introduction de nouvelles impuretés.

3 – INTRODUCTION DES IMPURETÉS DANS LE GERMANIUM ET LE SILICIUM

On a vu qu'avec les procédés de raffinage, on pouvait obtenir des barreaux de quelques décimètres de long (figure 5) et constitués de petits cristaux différemment orientés. On a obtenu des semi-conducteurs très purs, mais pour pouvoir les utiliser dans la fabrication des transistors et des diodes, il est nécessaire que les différents cristaux aient la même orientation dans un seul réseau cristallin, le Monocristal et il faut aussi "doper" le semi-conducteur c'est-à-dire y introduire des impuretés déterminées et dosées de façon à obtenir du germanium (ou du silicium) du type P ou N.

Les impuretés utilisées généralement pour obtenir un semi-conducteur P sont l'indium, l'aluminium, le galium, tandis que pour les semi-conducteurs N, on utilise de l'arsenic, du phosphore et de l'antimoine.

Habituellement, les monocristaux sont obtenus en introduisant à la surface du semi-conducteur en fusion, un cristal déjà parfaitement orienté, appelé "germe" (ou encore "amorce") et en faisant refroidir lentement la masse en fusion à partir de la zone de contact avec le germe.

Les impuretés qui auparavant étaient libres dans la masse en fusion, diffusent dans le monocristal pendant sa formation selon une loi qui dépend instant par instant de la rapidité de croissance du monocristal, de la concentration des impuretés dans la masse en fusion et de la constante de répartition des matériaux.

Dans le tableau de la figure 7, je vous ai reporté les valeurs moyennes des coefficients de répartition (constante d'isolement) du germanium et du silicium. Parmi les différentes valeurs, vous constatez que ce sont celles de l'indium qui sont les plus faibles : ceci indique que c'est la quantité d'indium qui diffuse dans le solide pendant le processus de recristallisation, que l'on peut contrôler avec le maximum de précision en ce sens que les doses à introduire dans la masse en fusion doivent être plus importantes pour obtenir le dopage et qu'ainsi on peut déterminer le poids avec le moins d'erreur possible.

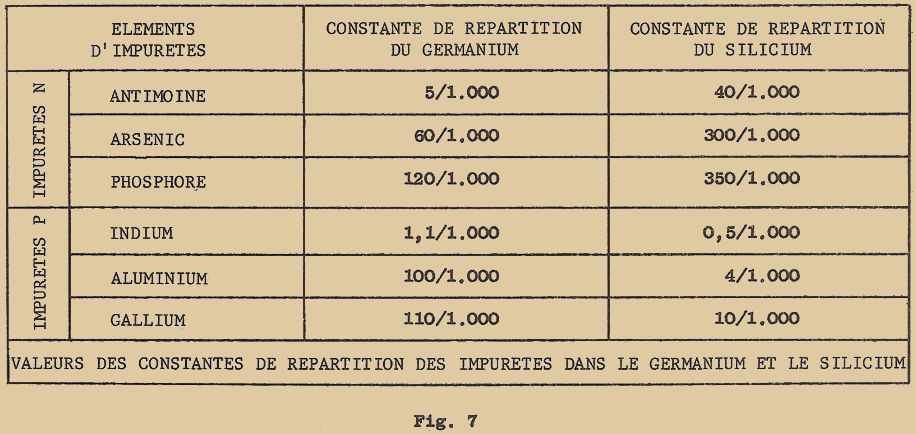
Examinons maintenant les deux méthodes principales utilisées pour obtenir les monocristaux de germanium dopés et qui sont : le procédé de "Nivellement" et le procédé "Tchiokralski". L'obtention des monocristaux de silicium ne diffère en ligne générale, que par l'appareillage utilisé, car il faut éviter à tout prix que le silicium en fusion ne se recombine avec les matériaux des coupelles qui introduiraient ainsi des impuretés indésirables.

3 – 1 "NIVELLEMENT" PAR LA ZONE DE FUSION MOBILE

Le barreau de germanium polycristallin est placé dans une coupelle de quartz, avec le germe, un liant d'impuretés et du graphite disposés comme sur la figure 8-a.

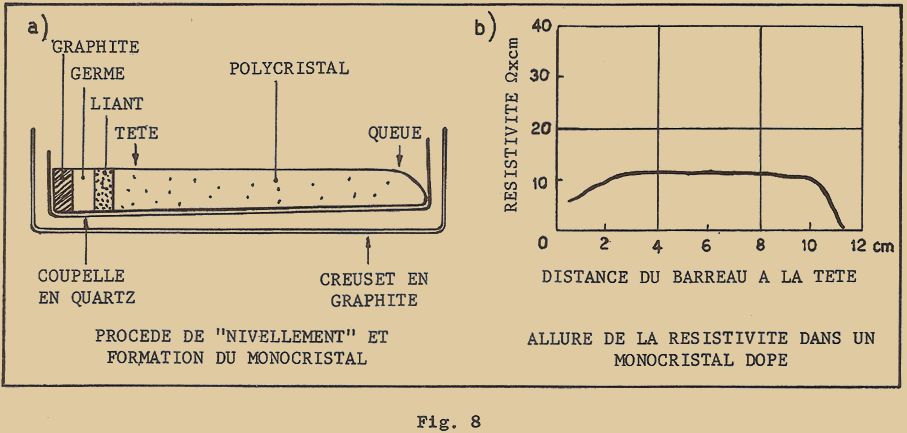
La coupelle de quartz est elle-même placée dans un creuset en graphite qui est introduit dans un four à induction constitué comme précédemment d'un tube en quartz et d'une bobine H.F.

On amène le creuset de graphite sous la bobine de façon à faire fondre le liant d'impuretés et la région correspondant à la tête du barreau, mais non le germe dont la structure interne doit rester intacte.

En déplaçant lentement le creuset, on amène la zone en fusion vers la queue du barreau, et débute alors une opération de refroidissement contrôlée, en partant de la section en contact avec le germe.

Une grande partie des impuretés reste isolée dans la masse liquide, tandis que la région restante (rigoureusement contrôlée) se fond dans le monocristal et grâce à un refroidissement contrôlé et progressif, croît sur le réseau du germe en conservant la même orientation.

À la fin de l'opération, c'est-à-dire lorsque l'on a obtenu une recristallisation compète du barreau, on retire un monocristal où toutes les impuretés primitivement contenues dans le liant ont diffusé.

La répartition des impuretés n'est pas encore uniforme et la résistivité du monocristal varie en fonction de la distance à la tête comme l'indique le graphique de la figure 8-b.

Dans la première partie, jusqu'à 4 cm environ, la résistivité augmente graduellement, ce qui indique que la concentration des impuretés décroît ; dans la seconde partie, entre 4 et 10 cm, elle se maintient constante, ce qui implique que la répartition des impuretés est uniforme ; dans la dernière partie, la résistivité décroît rapidement vers zéro, car c'est dans cette région que se trouvent concentrées toutes les impuretés.

On utilise donc uniquement la région centrale du barreau, car on a besoin d'un semi-conducteur dont la résistivité soit constante en tous points.

3 – 2 PROCÉDÉ TCHIOKRALSKI

Le monocristal peut encore être obtenu par étirage vertical à partir d'une solution de germanium et d'impuretés, maintenue en fusion dans un creuset spécial en graphite.

L'appareillage nécessaire fut réalisé par le polonais TCHIOKRALSKI dont le nom fut donné à cette méthode particulière de fabrication.

La figure 9 illustre l'installation d'étirage vertical que l'on utilise de façon courante.

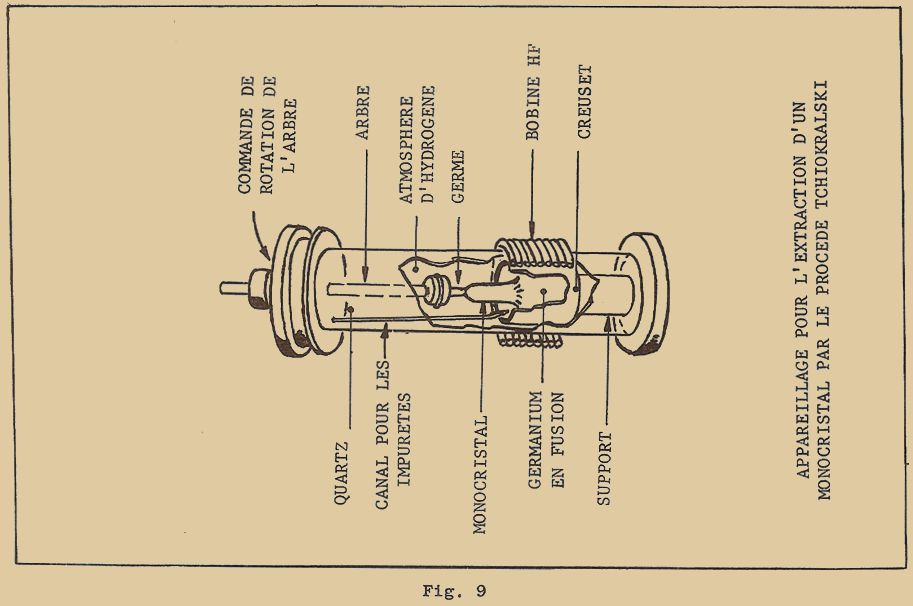
Dans le creuset, la masse liquide de germanium est maintenue à une température légèrement supérieure à celle qui correspond à la fusion.

Les impuretés sont introduites dans la solution à l'aide d'un petit tuyau. Un arbre tournant porte le germe et le place en contact avec la surface du liquide où un refroidissement local amorce l'opération de recristallisation.

En même temps, l'arbre se soulève lentement, de façon à ce que l'opération de cristallisation continue à se produire et détermine la "croissance" d'un monocristal orienté dans la direction de l'extraction.

Pour que les impuretés diffusent dans le monocristal, il faut encore prévoir une agitation continuelle de la masse en fusion, en imprimant à l'arbre une certaine vitesse de rotation. Il faut encore régler la vitesse de l'ascension, de façon à ne pas modifier la constante de répartition de chaque type d'impuretés.

Il faut de même contrôler la température à tout instant, car il suffit d'une variation de l'ordre de un degré centigrade pour compromettre toute la régularité de l'opération.

Avec l'appareillage décrit, il est possible d'obtenir des monocristaux dopés, alternativement du type P et du type N, en introduisant dans la solution, au moment voulu, l'impureté du type désiré.

Une autre méthode qui permet d'obtenir des monocristaux à régions alternativement P et N, consiste à régler la vitesse d'extraction en favorisant ainsi la diffusion d'un type d'impuretés par rapport à l'autre, qui sont mélangés simultanément dans la solution.

La figure 10 représente un monocristal à zones alternées. L'introduction des impuretés dans ces monocristaux nécessite un système de contrôle particulièrement rigoureux pendant l'opération d'extraction car il ne sera plus possible ultérieurement de modifier la structure des jonctions.

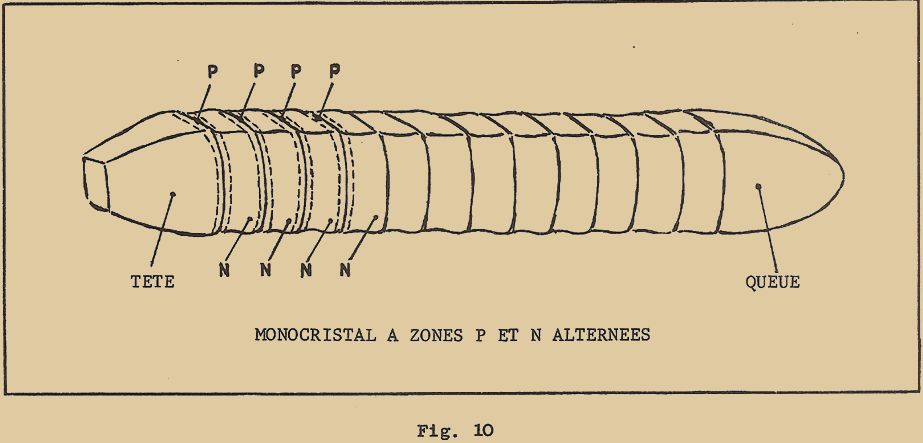
Les monocristaux à dopage uniforme (type P ou type N) obtenus par ce procédé, présentent une résistivité constante seulement dans la région centrale ce qui nécessite des contrôles rigoureux sur la résistivité, afin de limiter les régions utilisables.

4 - COUPE DES MONOCRISTAUX

Si les essais sur la résistivité s'avèrent corrects, on procède à la découpe des monocristaux en fines lamelles.

Pour cette opération, on utilise une scie circulaire à diamant : l'épaisseur du disque doit être faible.

Le monocristal à dopage uniforme (type P ou type N) est découpé selon des plans parallèles et perpendiculaires à l'axe de croissance, comme on peut le voir sur la figure 11-a. Le monocristal à zones alternées est découpé selon des plans parallèles longitudinaux et transversaux (figure 11-b).

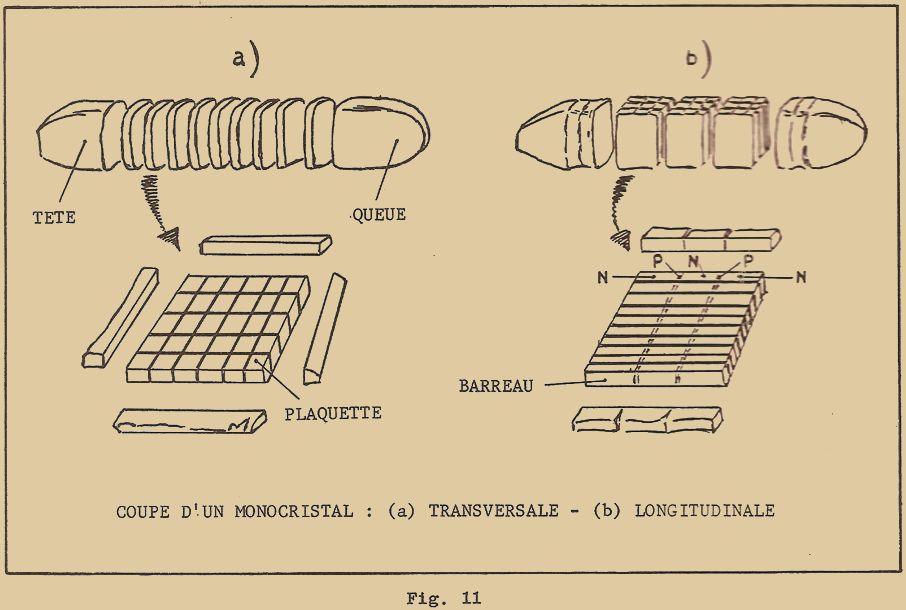
La détermination des plans de coupe dans le premier cas est justifié par le fait qu'à chaque instant pendant la croissance du monocristal on a une répartition uniforme des impuretés sur toute la section et que la résistivité d'une lamelle très fine peut être considérée comme rigoureusement constante ; au contraire, dans le second cas on doit faire une coupe de façon à obtenir des barreaux alternativement du type P et N, puis ensuite recoupés : la découpe est donc parallèle à l'axe de croissance.

Chaque lamelle subit ensuite un traitement de surface.

À partir des lamelles transversales on obtient, par une coupe ultérieure des plaquettes de semi-conducteurs N ou P ; à partir des lamelles longitudinales, on obtient des plaquettes alternativement P et N.

Dans la prochaine leçon, nous continuerons cette étude technologique et examinerons ensemble, les principales techniques de fabrication des diodes et des transistors.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 12^ème LEÇON THÉORIQUE

1 – La résistance statique est celle que le transistor présente en courant continu de polarisation ; la résistance dynamique est celle que le transistor présente en courant alternatif.

2 – Il y a quatre paramètres hybrides pour chaque type de montage.

3 – Les paramètres hybrides représentent respectivement la résistance d'entrée, la conductance de sortie, le coefficient d'amplification en courant et le coefficient de réaction en tension.

4 – Les unités de mesure des paramètres hybrides sont les suivantes : Ω ou kΩ pour h₁₁,mA/V pour h₂₂ ; sans dimension pour h₂₁ et h₁₂.

5 – Lorsque l'on donne les valeurs des paramètres hybrides, il faut toujours bien spécifier le type de montage, le point de fonctionnement et la température du transistor.

6 – Les valeurs des paramètres hybrides peuvent être mesurées directement sur le transistor à l'aide d'un montage adéquat, ou bien, peuvent être calculées sur les courbes caractéristiques.

7 – Lorsque la température du transistor s'élève au-dessus de la température ambiante, les valeurs des différents paramètres augmentent relativement peu pour h₁₁ et h₂₁, très vite pour h₂₂ et h₁₂

8 – Les paramètres "r" ne peuvent être mesurés directement mais peuvent être calculés à partir des paramètres hybrides.

9 – L'avantage principal des paramètres "r" par rapport aux hybrides est de n'avoir qu'une série de valeurs pour les différents montages possibles (en particulier émetteur commun et base à la masse).

---

EXERCICES DE RÉVISION SUR LA 13^ème LEÇON THÉORIQUE

1 – Pourquoi préfère-t-on extraire le germanium à partir des sous-produits du carbone ou des scories des minerais de zinc, plutôt qu'à partir des minerais de germanium ?

2 – Pourquoi la production du silicium en vue des besoins de l'électronique est-elle plus onéreuse que celle du germanium ?

3 – Pourquoi faut-il obtenir du germanium (ou du silicium) avec un très fort degré de pureté ?

4 – Qu'appelle-t-on coefficient de répartition (ou constante d'isolement) ?

5 – Pourquoi faut-il utiliser, dans la fabrication du silicium, des fours HF d'un type particulier ?

6 – Qu'appelle-t-on "semi-conducteurs polycristallins" ?

7 – Quel est l'avantage du procédé TCHIOKRALSKI par rapport au procédé utilisant la zone de fusion mobile ?

8 – Pourquoi faut-il contrôler la résistivité du barreau polycristallin et monocristallin ?

9 – Pourquoi faut-il faire la coupe d'un barreau monocristallin à zones alternées P et N en lamelles transversales ?

Fin de la leçon 13

---

LECON 14

TECHNOLOGIE DES TRANSISTORS

Les méthodes de fabrication des transistors sont nombreuses et différentes, mais en règle générale on peut les classer suivant les quatre procédés fondamentaux, qui permettent d'obtenir des jonctions de redressement : jonctions métalliques – jonctions par alliage – jonctions obtenues par étirage (ou croissance contrôlée) – jonctions par diffusion.

Dans la première partie de cette leçon, nous ferons un résumé des différents procédés en nous limitant aux fabrications des diodes et des transistors.

1 – TECHNIQUE DES JONCTIONS

La jonction électrique des matériaux consiste en un contact plus ou moins large qui intéresse la structure moléculaire même de ces matériaux au point de jonction et peut en modifier la conductibilité.

Si le courant continu peut traverser la surface de la jonction dans les deux sens en rencontrant la même résistance, on dit que l'on a une jonction ohmique ; si la résistance est élevée dans un sens et faible dans le sens opposé, on dit que l'on a une jonction de redressement.

Ces deux types de jonctions existent, simultanément dans les transistors et dans les diodes. Le premier type (ohmique) sert à établir les branchements des fils de sortie ("pattes" du transistor) ; le second type (redressement) constitue l'élément actif qui est la base même du fonctionnement électronique des semi-conducteurs.

Par simplification et pour éviter toute erreur possible, nous appellerons connexion (ou liaison) la jonction "ohmique" et jonction la "jonction de redressement".

Vous trouverez dans les figures 1 et 2, présentés de façon schématique, les quatre procédés permettant d'obtenir des jonctions.

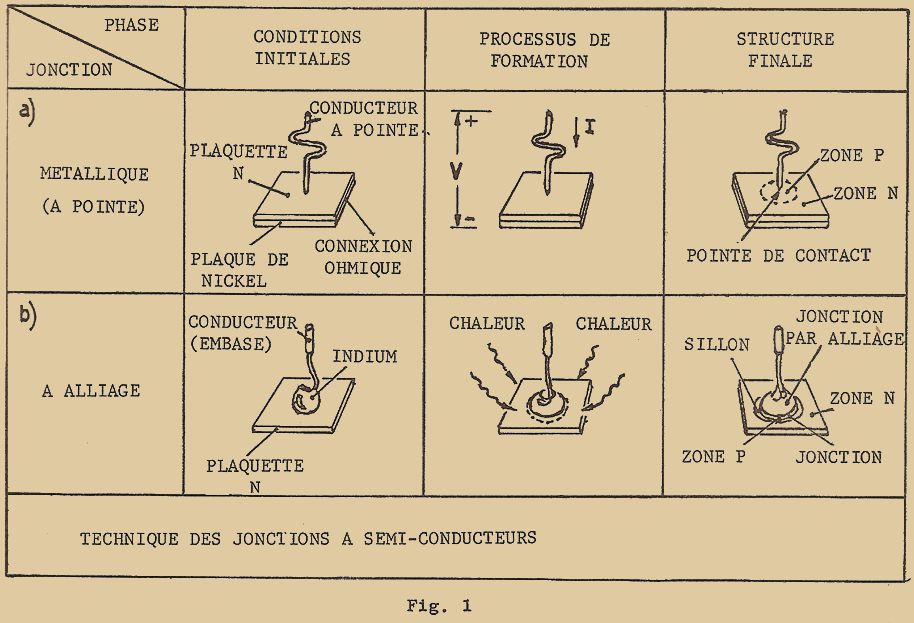
1 – 1 JONCTION METALLIQUE (figure 1-a)

Nous avons vu précédemment, comment étaient préparés les semi-conducteurs pour les utilisations en électronique et comment on obtenait des monocristaux présentant des conductibilités P ou N.

Pour utiliser ces plaquettes, il faut former une jonction de redressement P-N sans en modifier le réseau cristallin. C'est la méthode qui avait été adoptée pour fabriquer les premières diodes et les premiers transistors et qui encore maintenant est utilisée dans la construction de différents types de diodes et de quelques types de transistors.

On place sur la plaquette un morceau de nickel ou tout autre conducteur qui a pour rôle d'assurer un contact ohmique de faible résistance, et sur la face opposée de cette même plaquette on appuie la pointe d'un fil de tungstène, d'or ou d'un alliage métallique.

S'il s'agit d'une plaquette de silicium P, un simple contact de la pointe suffit pour obtenir une jonction de redressement.

Si au contraire on utilise une plaquette de germanium N, comme il est indiqué sur la figure 1-a, pour obtenir une jonction il faut encore envoyer une impulsion de courant I de la pointe vers la plaquette.

L'échauffement dû au passage du courant détermine une redistribution des impuretés dans la zone du monocristal qui entoure le point de contact et favorise ainsi la diffusion de nouveaux éléments d'impuretés en provenance du fil de façon à former une zone P superposée à la zone N d'origine.

Le mélange intime de deux zones dans le même cristal constitue une jonction de redressement. On peut obtenir encore un résultat analogue au précédent, en soudant sur la plaquette N, un fil très fin d'or contenant un très faible pourcentage de gallium.

La jonction obtenue par contact soudé a des caractéristiques meilleures que celles obtenues par simple contact de pointe, parce que la connexion est plus résistante tant du point de vue mécanique que thermique.

Le branchement des connexions externes est fait en soudant (au moyen de l'étain ou autre matériau) les "pattes" de sortie sur la plaque de nickel et sur le fil de tungstène ou d'or. La jonction redresseuse obtenue par les méthodes qui viennent d'être décrites est dite métallique, car à l'origine, une des deux électrodes, c'est-à-dire le fil, est constitué par un métal ou un alliage métallique (tungstène, or, cuivre phosphoreux, cuivre et béryllium, etc …) et l'effet redresseur provient essentiellement des modifications dûes au contact entre le métal et le semi-conducteur dopé de la plaquette.

1 – 2 JONCTION PAR ALLIAGE (figure 1-b)

C'est le type de jonction qui est le plus utilisé actuellement dans la fabrication industrielle des transistors.

On place sur la plaquette une minuscule sphère ou un petit disque d'un matériau qui contient une forte proportion d'impuretés : par exemple de l'indium, ou d l'indium-gallium, si la plaquette présente une conductibilité N comme indiqué sur la figure 1-b.

La plaquette, le disque et un fil de cuivre qui sert de connexion sont placés dans un four spécial et sont portés à une température qui dans le cas de l'indium et du germanium N est de l'ordre de 550 – 600°C.

Le temps de chauffage à cette température n'est pas très critique mais doit dépasser deux ou trois minutes.

Remarquons que dans le cas présent, l'indium fond à 160°C environ et le germanium à 950°C environ.

Tant que la température est inférieure à 160°C, le germanium et l'indium restent à l'état solide ; lorsqu'elle dépasse au contraire 160°C, l'indium fond et une partie du germanium au contact avec la masse en fusion se transforme en donnant un alliage.

Dans cet alliage, le pourcentage du germanium augmente avec la température jusqu'à ce que cette dernière atteigne 950°C où alors tout le germanium se trouve à l'état de fusion et on obtient une solution liquide des deux éléments.

Le procédé est représenté par le graphique de la figure de la figure 3.

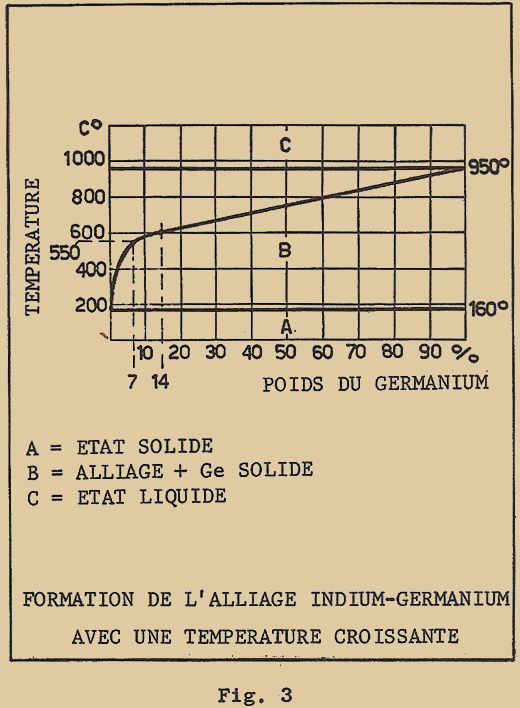
Si l'on examine la courbe, on remarque qu'à 550°C, le pourcentage du germanium entré dans l'alliage est de 7% environ, tandis qu'à 600°C, il a doublé et est devenu 14%. Ceci indique donc que la température est très critique, puisqu'il suffit d'une variation relativement faible de celle-ci (50° sur 550°C) pour introduire une variation notable dans la concentration germanium-indium. En pratique, pour que le procédé par alliage donne de bons résultats, il faut maintenir les variations maximales de la température entre ± 5°C de la valeur fixée.

Lorsque l'alliage s'est formé, on laisse refroidir très lentement le four. Pendant cette seconde phase, l'alliage se solidifie en faisant croître sur la structure de la plaquette, une couche P intimement liée avec la couche N d'origine, et il se forme ainsi une jonction redresseuse P-N.

La région supérieure où est fixé le fil constitue une jonction ohmique qui sert à relier la zone P à la connexion externe.

À la fin du processus, on creuse un sillon autour de la jonction, de façon à supprimer le court-circuit qui se forme en général entre la zone supérieure de l'alliage et la couche N de la plaquette.

1 – 3 JONCTION PAR ETIRAGE (CROISSANCE CONTRÔLÉE) (figure 2-c)

Une autre technique qui a un certain succès est basée sur la possibilité d'obtenir une jonction P-N en modifiant la vitesse d'extraction du monocristal lors du procédé TCHIOKRALSKI.

Nous avons vu dans la dernière leçon comment on pouvait obtenir par ce procédé, des jonctions multiples à couches P et N alternées, en exploitant la dépendance qui existe entre le coefficient de répartition des impuretés et la vitesse d'extraction. Pour mieux comprendre encore ceci, nous allons examiner quelques-unes des données les plus significatives.

Lorsque la vitesse d'extraction du monocristal est très lente, le coefficient de répartition de l'arsenic dans le germanium est de l'ordre de 20/1.000 ; cette valeur passe à 65/1.000 pour une vitesse de l'ordre de 5 cm à l'heure et à 150/1.000 pour une vitesse de 30 cm à l'heure.

En considérant de telles données, il devient évident qu'en faisant varier la vitesse d'extraction on peut obtenir dans le monocristal des zones où les impuretés d'arsenic sont plus ou moins importantes.

Si l'on met au contraire dans le germanium en fusion, de l'aluminium (dont le coefficient de répartition est de 100/1.000 et reste à peu près constant dans la gamme des vitesses considérées pour l'arsenic), on obtient une zone N dans laquelle prévaut l'arsenic et si la vitesse est faible on obtient une zone P où c'est l'aluminium qui prévaut.

Les zones ainsi obtenues sont intimement liées dans la structure du monocristal et constituent une succession de jonctions redresseuses P-N.

Par une coupe mécanique spéciale, on obtient des barreaux dans lesquels la structure finale de la diode ou du transistor est déjà déterminée ; pour compléter le dispositif, il suffit d'établir les connexions correspondantes.

1 – 4 JONCTION PAR DIFFUSION (figure 2-d)

La technique de la diffusion est plus récente et a été introduite pour améliorer la réponse en fréquence des transistors. Elle consiste à faire pénétrer à travers la surface très faible, du monocristal et jusqu'à une certaine profondeur, un type donné d'impuretés qui détermine la formation d'une zone N dans le semi-conducteur P d'origine, ou bien d'une zone P dans un semi-conducteur N d'origine.

A ses débuts, la technique de diffusion s'était développée comme une variante de la méthode par étirage décrite ci-dessus.

Au lieu d'agir sur la vitesse d'extraction du monocristal, on introduisait dans le liquide en cours de solidification, des quantités choisies et dosées d'un matériau, alternativement du type P et N.

Par cette méthode, en augmentant tantôt la dose P, tantôt la dose N, on pouvait obtenir des jonctions P-N pendant la croissance du cristal. La diffusion s'obtenait à travers la surface de séparation entre le liquide et le solide, et comme pour le procédé par étirage, le degré de diffusion dépendait de la constante de répartition des éléments d'impuretés dans le semi-conducteur.

Une autre méthode actuellement plus en vogue, consiste à faire évaporer sous vide, ou dans une atmosphère de gaz inerte, des matériaux d'impuretés et à exposer ainsi à la vapeur la surface de la plaquette (figure 2-d). En portant la température de la plaquette et de la vapeur à une valeur convenable, les atomes d'impuretés pénètrent dans le réseau cristallin même de la plaquette avec une concentration qui décroît en fonction de la profondeur comme le montre le graphique de la figure 4. Au niveau de la surface, la concentration des atomes diffusés est de l'ordre de 10¹⁹ atomes/cm³ c'est-à-dire 10 milliards de milliards d'atomes dans 1 cm³ de semi-conducteur ; à une profondeur de 20 µ seulement (1 µ = 1 millième de mm) la concentration n'est plus que de 10⁵/cm³, c'est-à-dire 100.000 atomes dans 1 cm³.

Les impuretés diffusées doivent être du type opposé à celui de la plaquette et étant donné leur forte concentration à la superficie, elles prédominent nettement en formant une couche N si le semi-conducteur d'origine est P, ou bien une couche P si le semi-conducteur était N.

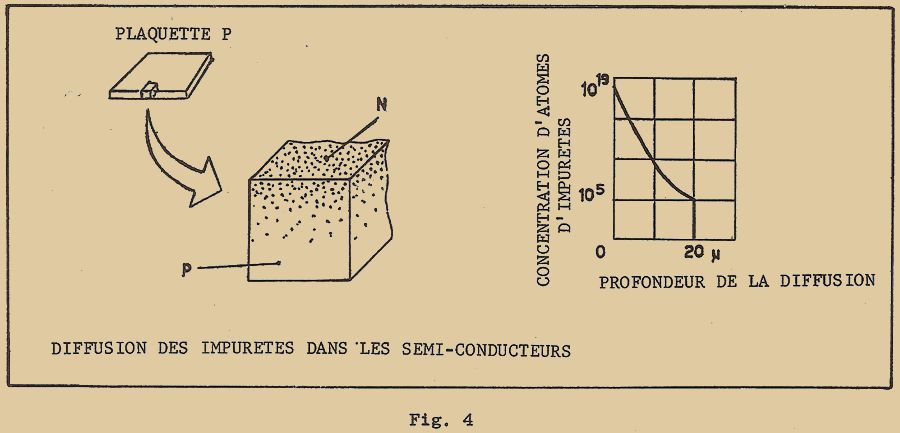
La jonction P-N ainsi obtenue présente des caractéristiques meilleures que celles obtenues par la méthode d'étirage ou d'alliage ; de plus, cette méthode permet d'obtenir des effets particuliers qui déterminent une réduction sensible du temps de transit des charges dans les semi-conducteurs et comme nous le verrons plus tard, est particulièrement adaptée pour la fabrication des transistors pour haute fréquence.

2 – MONTAGE DES DIODES ET DES TRANSISTORS

La diode à semi-conducteur consiste essentiellement dans une jonction P-N obtenue par une des méthodes décrites ci-dessus.

On part d'une plaquette et on forme la diode par le procédé de la jonction métallique, ou par le procédé d'alliage ou par diffusion.

La plaquette est successivement exposée à une attaque chimique puis à un abondant lavage en eau désionisée (électriquement neutre) pour éliminer des court-circuits éventuels entre la surface externe des régions P et N. Dès qu'elle est sèche, la plaquette est prête à recevoir les fils de liaisons extérieures.

La formation d'un transistor est obtenue soit en partant d'une plaquette et en y établissant deux jonctions P-N, soit en partant d'un barreau dans lequel les deux jonctions se trouvent déjà formées par étirage ou bien par étirage et diffusion.

La plaquette et le barreau qui constituent l'élément actif du transistor, sont exposés aussi à une attaque chimique puis à un lavage de façon à éliminer des court-circuits éventuels de surface.

Les modalités de l'exécution du montage peuvent différer notablement selon le type de jonction et selon le procédé imposé par le constructeur. Nous allons examiner séparément les descriptions de quelques diodes et transistors d'emploi général.

2 – 1 DIODES À POINTES

A la figure 5-a, on peut voir comment est réalisée une diode à pointe. Les embases des connexions externes sont placées à l'intérieur de l'enveloppe de verre. Sur l'embase de l'anode est soudé un fil de tungstène plié en "S" de façon à présenter un certain jeu élastique dans la direction longitudinale. La plaquette est soudée à l'aide d'un alliage d'étain sur l'embase de la cathode.

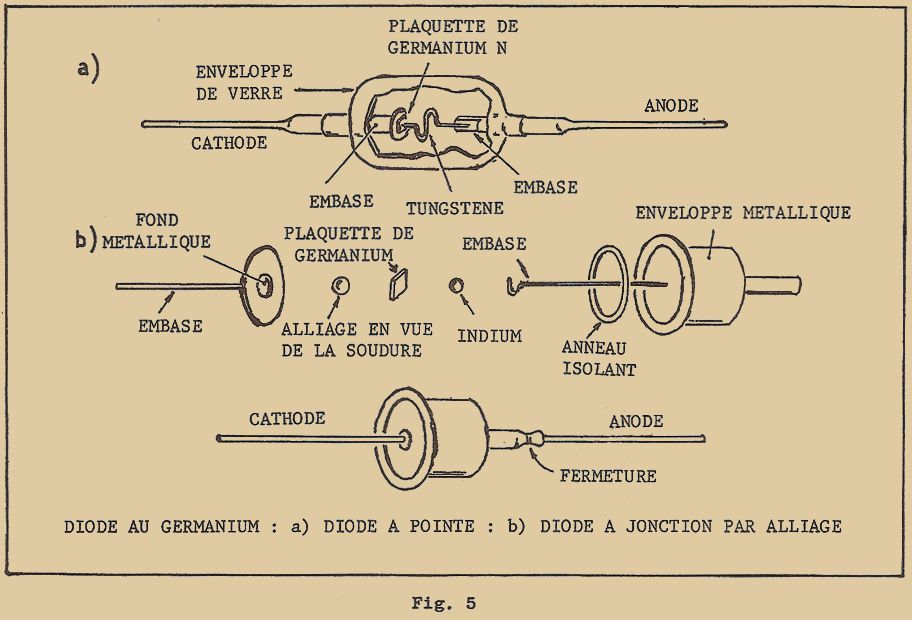
Pendant la phase de montage, l'opérateur contrôle la pression de la pointe et le processus de formation de la jonction métallique.

Après un contrôle des caractéristiques électriques aux différentes conditions de fonctionnement, on procède à la fermeture hermétique de l'enveloppe.

2 – 2 DIODES À JONCTION PAR ALLIAGE

A la figure 5-b, on peut voir les différents éléments séparés pour la réalisation d'une diode par alliage.

Nous avons vu sur la figure 1-b, comment était formée la jonction redresseuse et comment on branchait sur la zone P l'embase correspondante (fil de sortie). La plaquette est soudée sur le fond métallique de façon à obtenir une jonction ohmique à faible résistance.

On fixe ensuite, le fond sur la base de l'enveloppe de façon à obtenir une fermeture hermétique. Puis pour terminer, on ferme l'enveloppe sous vide après avoir soudé le fil extérieur d'anode.

La figure 6 représente la structure interne d'une diode par alliage pour des tensions et des courants moyens.

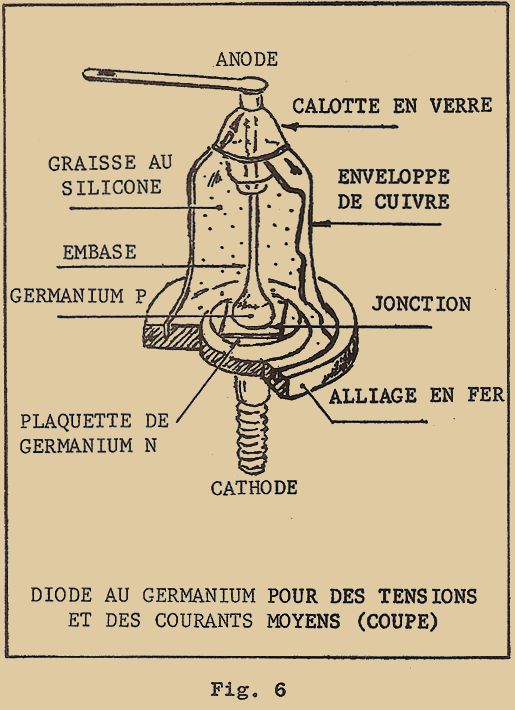
La technique de fabrication ne diffère pas notablement de celle qui a été décrite ci-dessus. Il suffit de remarquer qu'étant donné que le dispositif doit dissiper une certaine puissance sous des tensions relativement élevées, il faut prévoir un bon isolement de l'anode au travers de la calotte de verre. D'autre part la forme de l'enveloppe et les matériaux utilisés sont tels qu'ils permettent une dissipation thermique optimum.

Les sections des conducteurs sont dimensionnées de façon à pouvoir supporter les fortes intensités de courants prévues.

L'enveloppe est remplie de graisse au silicone qui sert à éviter des altérations superficielles de la jonction et à amortir des vibrations éventuelles du système dûes à des sollicitations mécaniques extérieures.

Si l'on désire améliorer la dissipation thermique de la diode, on fixe à l'aide d'un écrou, une plaquette métallique qui fonctionne comme ailette de refroidissement.

2 – 3 DIODE À JONCTION DIFFUSÉE

Le système de montage de la diode représentée à la figure 7 est analogue aux précédents ; toutefois, si l'on examine le dessin, on peut noter quelques différences de structure.

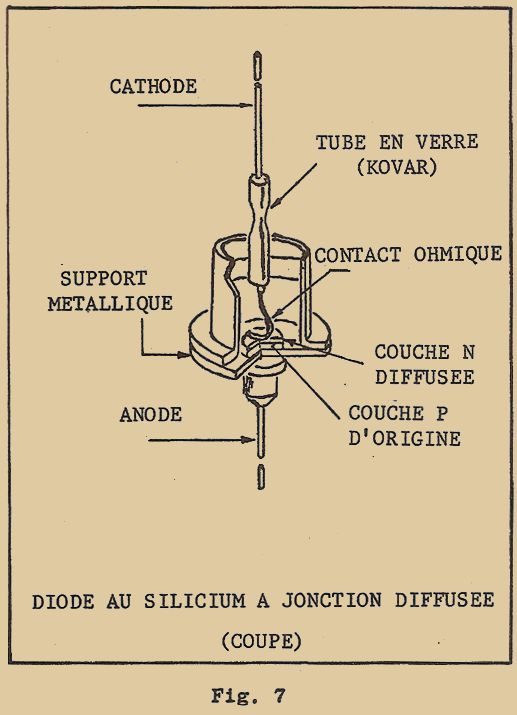
L'embase de cathode, qui dans les types précédents était connectée sur la base métallique de l'enveloppe, est maintenant isolée et connectée à un tube en KOVAR (alliage de Nickel, Cobalt, Manganèse et Fer soudable au verre) qui assure l'étanchéité à la traversée du verre.

Il faut encore se rappeler que pendant le montage l'opérateur doit pouvoir contrôler les jonctions ohmiques des connexions, tandis que dans les diodes à alliage une connexion était établie pendant le processus même de l'alliage.

Si l'on utilise une plaquette de silicium P avec une couche diffusée N, il est plus facile d'établir un large contact ohmique sur la surface de la couche d'origine P par l'intermédiaire d'un second traitement qui consiste dans une diffusion superficielle de bore. Par un tel procédé on peut souder la couche P à la base de l'enveloppe et obtenir ainsi une faible résistance ohmique de contact.

Le branchement de la connexion de sortie de cathode sur la couche N se fait par un procédé spécial dit de thermocompression.

Le procédé consiste à comprimer l'extrémité d'une lamelle de nickel et à chauffer rapidement et pendant un court instant la zone de contact jusqu'à obtenir la soudure des deux ensembles.

Les diodes de ce type, comme celle de la figure 6, appartiennent à la catégorie des diodes de puissance.

Il existe encore bien d'autres techniques, mais en règle générale elles se ramènent toutes aux opérations fondamentales qui ont été examinées dans cette leçon.

2 – 4 TRANSISTORS À JONCTION PAR ALLIAGE PNP

Dans la production industrielle des transistors, la technique des jonctions métalliques à pointes a été abandonnée ainsi que celles des jonctions obtenues par étirage contrôlé. Actuellement, les transistors d'utilisation courante sont fabriqués par la méthode de la jonction par alliage, quelquefois aussi par le procédé de la diffusion et des jonctions métalliques obtenues par soudage. Ces procédés, assez récents, rencontrent un succès croissant dans la fabrication des transistors pour hautes fréquences.

Pour illustrer le procédé du montage des transistors, je vais vous décrire les deux méthodes que l'on peut considérer comme typiques.

TRANSISTOR PNP (PAR ALLIAGE) POUR DES PUISSANCES INFÉRIEURES À 1 W

Les phases principales de la fabrication et du montage sont illustrées à la figure 8.

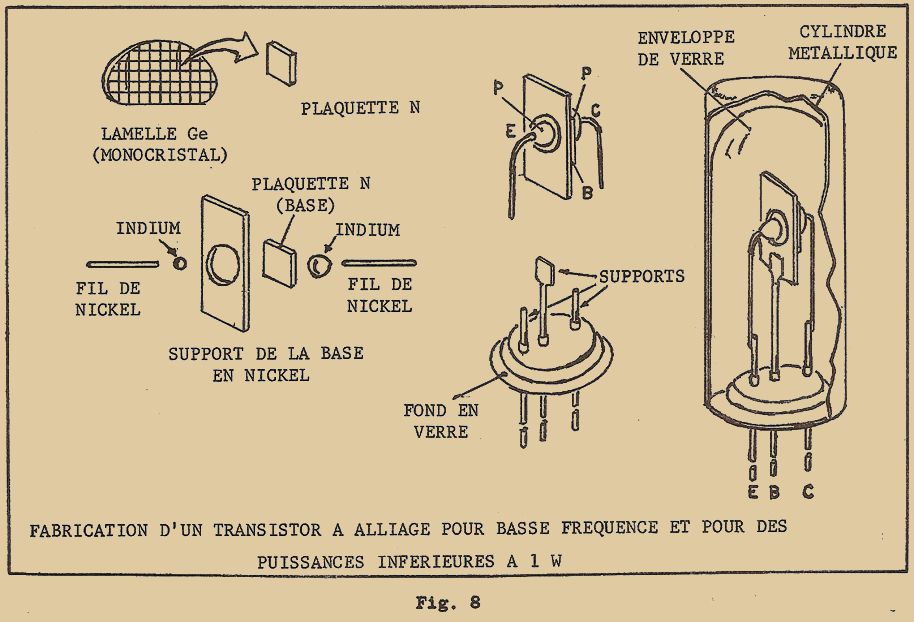
La plaquette de germanium N a environ 2,5 mm de côté et quelques dixièmes de millimètre d'épaisseur. On forme sur celle-ci, deux jonctions P-N par alliage : celle de l'émetteur (à gauche) et celle du collecteur (à droite). On observera que la quantité d'indium utilisée pour la jonction de l'émetteur est inférieure à celle utilisée pour la jonction du collecteur.

La zone N, qui sépare les deux zones P obtenues par le procédé de l'alliage, constitue l'électrode de base. Sur cette électrode sera placé le support en nickel par soudage sur la plaquette. Cette opération est effectuée en prenant soin de ne pas provoquer de court-circuit avec la région P de l'émetteur.

Pendant l'opération de l'alliage, on connecte respectivement à l'émetteur et au collecteur deux fils de nickel (ou de cuivre) qui serviront de fils de sortie et qui sont reliés aux supports des électrodes. Cette opération s'effectue par soudage électrique.

L'ensemble est ensuite placé dans une enveloppe de verre remplie de graisse au silicone dont la fonction est la même que pour les diodes de la figure 6.

Si l'on a affaire à des transistors de faible puissance, on peint l'enveloppe en noir pour protéger son contenu de la lumière. S'il s'agit de transistors de puissance, on protège l'enveloppe de verre par un cylindre métallique dont le but est d'abord de protéger le dispositif de la lumière et ensuite d'améliorer la dissipation thermique.

TRANSISTOR PNP (PAR ALLIAGE) POUR DES PUISSANCES ÉGALES OU SUPÉRIEURES À 1 W

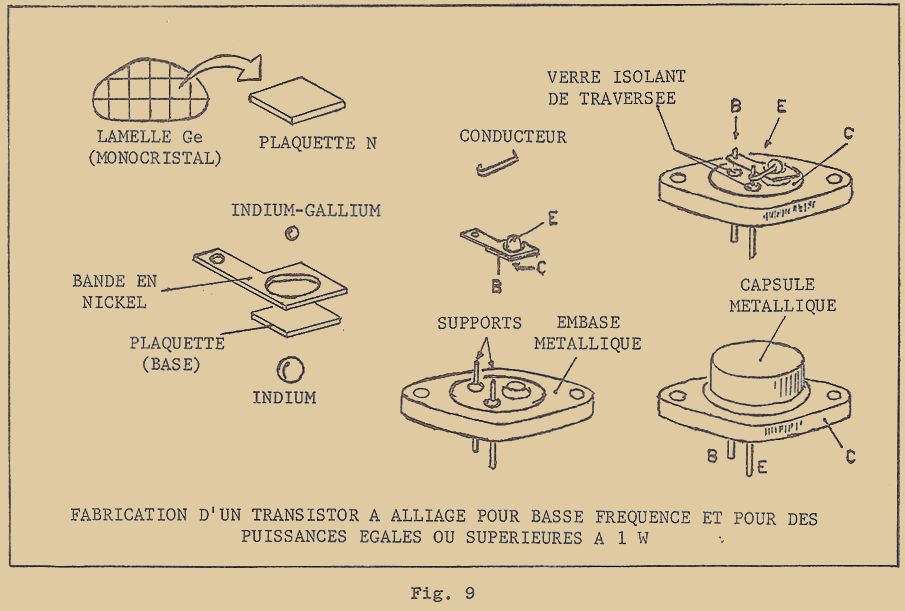
La technique de la formation des deux jonctions (émetteur et collecteur) est identique à celle utilisée ci-dessus, mais l'exécution du montage (illustré à la figure 9) est différente car il s'agit d'obtenir un dispositif robuste qui puisse supporter le maximum de puissance et dissiper toute la chaleur crée pendant le fonctionnement.

On utilise dans ce but, des plaquettes relativement grandes (de 5 mm de côté environ et quelques dixièmes de mm d'épaisseur). Les conducteurs ont des diamètres de l'ordre du millimètre et une enveloppe métallique montée sur le fond, lui aussi métallique, de façon à former un bloc compact ayant une bonne dissipation thermique. D'autre part l'électrode du collecteur, qui est la plus sujette à l'échauffement, est reliée directement à la masse métallique du boîtier, qui forme ainsi la connexion externe de collecteur.

Dans l'ensemble, la structure du dispositif est compacte et très résistante tant du point de vue thermique que mécanique.

3 – TRANSISTORS À JONCTION ET CARACTÉRISTIQUES DÉPENDANT DES MODALITÉS DE CONSTRUCTION ET DE MONTAGE

Toute la technique de fabrication des transistors est tributaire de la nécessité d'obtenir des matériaux à très grand degré de pureté et de ne pas contaminer ces matériaux lors des différentes manipulations.

Du degré de pureté des différents matériaux, dépend l'allure de la résistivité et la valeur de la tension inverse maximum que l'on peut appliquer entre les électrodes du dispositif.

Des précautions prises pour éviter les contaminations dûes à l'humidité, à la poussière ainsi qu'à des contacts avec des agents chimiques, dépend en grande partie l'uniformité des caractéristiques électriques et par voie de conséquence le coefficient d'amplification β.

Il suffit de se rappeler qu'une variation quelconque dans les opérations avant la fermeture de l'enveloppe peut faire diminuer la valeur du coefficient β et provoquer un accroissement notable du courant inverse de collecteur.

Les différents contrôles de température dépendent la régularité du monocristal, l'épaisseur de la base des transistors alliés, la profondeur de la diffusion et la concentration des impuretés. De l'ensemble de ces quatre facteurs dépend en définitif, la réponse en fréquence du transistor.

A ses débuts, quand le transistor n'avait pas encore quitté les laboratoires de recherches, on a dû résoudre tous les problèmes de la métallurgie des semi-conducteurs (que nous avons vus dans la précédente leçon) avant d'atteindre une qualité industrielle avec des caractéristiques électriques uniformes et reproductibles. Il a fallu ensuite surmonter les trois des plus importantes limitations du transistor par rapport au tube électronique : la dispersion des caractéristiques, la limite de puissance, la limite de réponse en fréquence.

Le problème de la dispersion des caractéristiques a été résolu par différents constructeurs de façon empirique en prenant de grandes précautions pour garantir la pureté des matériaux, la régularité dans la structure cristalline et la pureté des surfaces.

Le problème de la puissance a été résolu ensuite, comme nous l'avons vu, en augmentant la section des conducteurs et les surfaces des éléments actifs, en perfectionnant l'isolement des électrodes et la dissipation thermique de l'enveloppe.

Il nous reste encore à voir, comment on a cherché à résoudre sur le plan de la production industrielle, le problème de la réponse en fréquence, problème qui n'est pas encore complètement résolu, bien que des progrès très sensibles aient été obtenus.

4 – TRANSISTORS POUR HAUTES FRÉQUENCES

Le transistor, comme nous allons le voir dans les prochaines leçons, atténue l'amplitude des signaux aux fréquences élevées. Ceci provient du fait que pour passer d'une jonction à l'autre, c'est-à-dire pour franchir l'épaisseur de la base, les charges électriques suivent un processus de diffusion qui est beaucoup plus lent que dans un circuit électrique classique.

Pour améliorer la réponse en fréquence d'un transistor, il faut diminuer le temps de transit des charges dans l'électrode de la base.

Le résultat peut être obtenu de deux façons différentes :

• ou bien en réduisant l'épaisseur de la base
• ou bien en accélérant ces charges

Avec la technique des jonctions alliées, il est possible d'obtenir des épaisseurs de la base de l'ordre de quelques microns avec des tolérances de ± 1,5 µ et d'avoir ainsi des fréquences de coupure de 15 MHz environ pour des transistors PNP et 30 MHz pour des transistors NPN. Mais avec ce procédé, on diminue le rendement de la production, à cause des risques de court-circuits entre émetteur et collecteur. D'autre part, avec les écarts plus ou moins grands dans la détermination de l'épaisseur de la base, on a une dispersion importante dans les fréquences de coupure.

Avec la technique de la diffusion il est devenu impossible de mieux régler l'épaisseur de la base, d'accélérer les charges pour obtenir ainsi une réduction importante dans le temps de transit et une amélioration dans la réponse aux hautes fréquences.

Nous avons vu (figure 4) qu'en exposant une plaquette à des vapeurs d'impuretés, on obtenait une pénétration de celles-ci en concentration décroissante ; cette répartition particulière des éléments diffusés est appelée "GRADIENT d'impuretés".

Pour fixer les idées, supposons que l'on utilise comme électrode de base une plaquette N à gradient d'impuretés (figure 10).

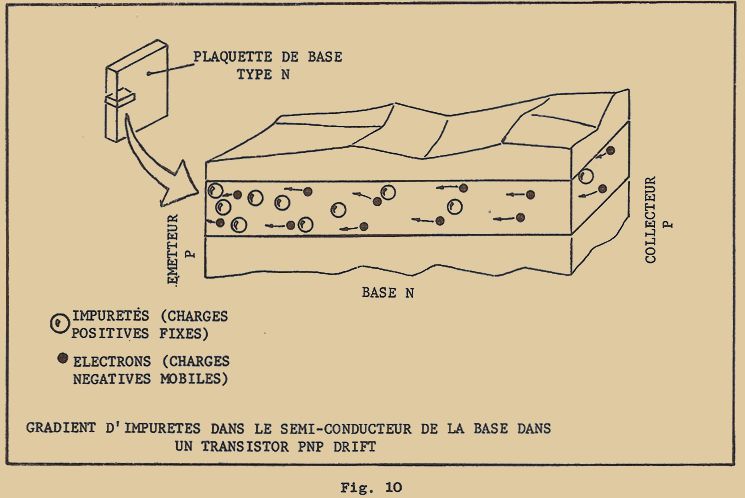
Les atomes d'impuretés (boules blanches) constituent autant de charges positives fixes dont la concentration varie tout le long de l'épaisseur de la base, tandis que les électrons (boules noires) sont des charges négatives mobiles.

Etant donné que les charges électriques mobiles ont tendance à se répartir uniformément dans les conducteurs et que les électrons sont libres de se mouvoir, on aura une distribution presque uniforme des électrons dans la base.

A cause de la diffusion des électrons, il se crée du côté de l'émetteur (c'est-à-dire là où la concentration des impuretés est la plus grande) un excès de charges positives, tandis que du côté du collecteur (là où la concentration est la plus faible) on a un excès d'électrons. Le phénomène décrit à la figure 10 est représenté schématiquement sur la figure 11.

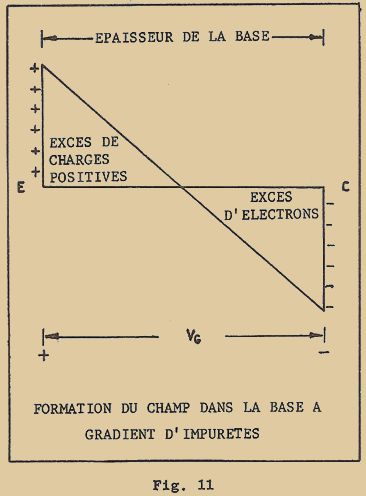
La distribution différente des charges détermine et maintient un champ électrique, c'est-à-dire une différence de potentiel entre les surfaces de la base. Le champ est polarisé de sorte que le positif est du côté de l'émetteur et le négatif du côté du collecteur. Ainsi les électrons qui proviennent de la borne négative de la pile et qui pénètrent dans la base au travers de la jonction de collecteur sont attirés par le champ positif et se trouvent accélérés, d'où réduction sensible du temps de transit.

Le phénomène qui vient d'être décrit est appelé communément DRIFT, terme anglais qui signifie : "pousser" ; en effet les électrons reçoivent une "poussée" du champ électrique vers la jonction opposée, c'est-à-dire vers l'émetteur dans les transistors PNP.

4 – 1 TRANSISTORS DRIFT

L'effet drift se manifeste d'une manière plus ou moins efficace dans tous les transistors, sauf dans ceux dont les jonctions sont formées par alliage ou dans les jonctions métalliques. Ceci est évident si l'on compare les profils de la variation de la résistivité dans la base (figure 12)

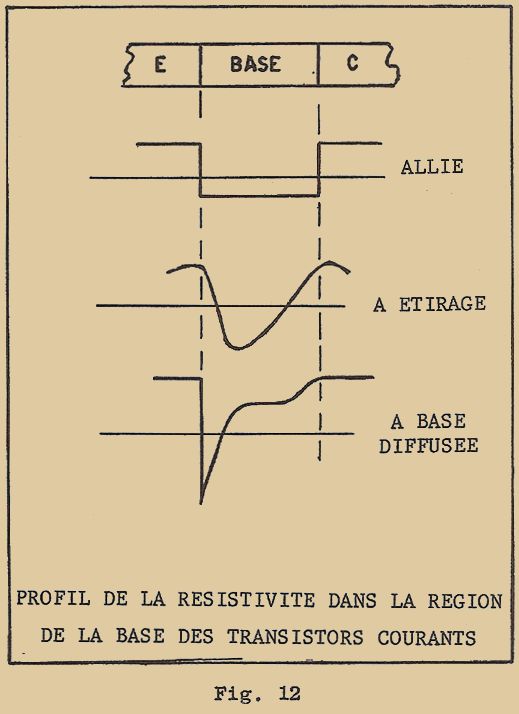
Les transistors obtenus par étirage ou par diffusion présentent une chute de résistivité du côté de l'émetteur (chute plus ou moins rapide) et une augmentation progressive de la résistivité de la base vers le collecteur. Cette allure de la résistivité, indique la présence d'un gradient dans la distribution des impuretés, c'est-à-dire la présence d'un champ accélérateur. Avec la technique combinée des procédés par alliage et par diffusion, on fabrique actuellement des transistors dans lesquels l'effet drift est exploité au maximum.

Les transistors sont appelés transistors DRIFT et on obtient avec ceux-ci des fréquences de coupure élevées, de l'ordre de quelques dizaines de mégahertz.

4 – 2 TRANSISTORS MESA

La limitation fondamentale du transistor drift est dûe à l'imprécision du contrôle de l'épaisseur de la base, imprécision déjà remarquée dans le transistor allié.

Une amélioration sensible du problème est représentée par le transistor MESA. La figure 13 donne l'illustration du montage type de ce transistor et le schéma des deux jonctions.

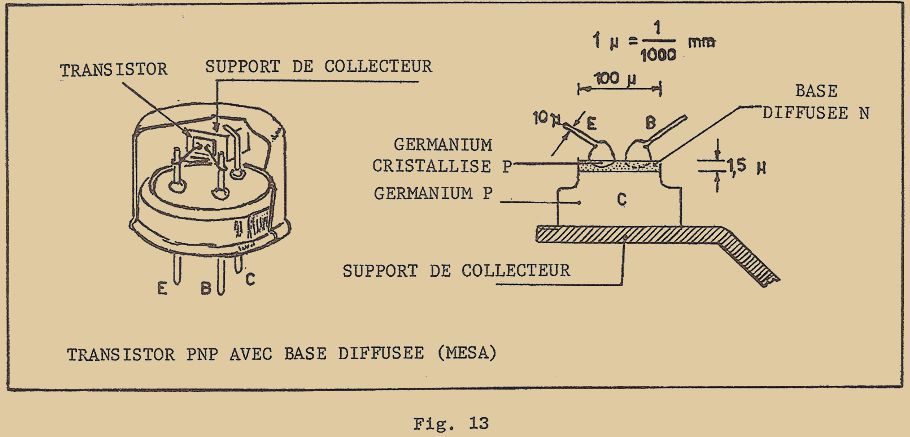
Le collecteur est constitué par une plaquette de germanium P sur laquelle on vient diffuser la zone de la base. L'épaisseur de la région diffusée peut être contrôlée avec une précision de l'ordre de 0,1 µ. La jonction de l'émetteur est formée sur la surface externe de la base par un procédé d'alliage particulier, appelé "micro-alliage".

Sur la surface même où se formera l'émetteur, est placé le support de la connexion de la base, de telle façon que son profil ressemble à certaines montagnes d'Amérique du Sud appelée mesa. C'est de cette similitude que dérive le nom de Mesa donné à ces transistors.

Avec cette nouvelle réduction de l'épaisseur de la base, et grâce à l'effet drift qui existe toujours, on a pu diminuer encore le temps de transit des charges dans la base et repousser la fréquence de coupure de quelques centaines de mégahertz et couvrir ainsi la gamme des fréquences FM et TV.

5 – RÉSUMÉ SUR LES DONNÉES TECHNIQUES DE FABRICATION DES TRANSISTORS

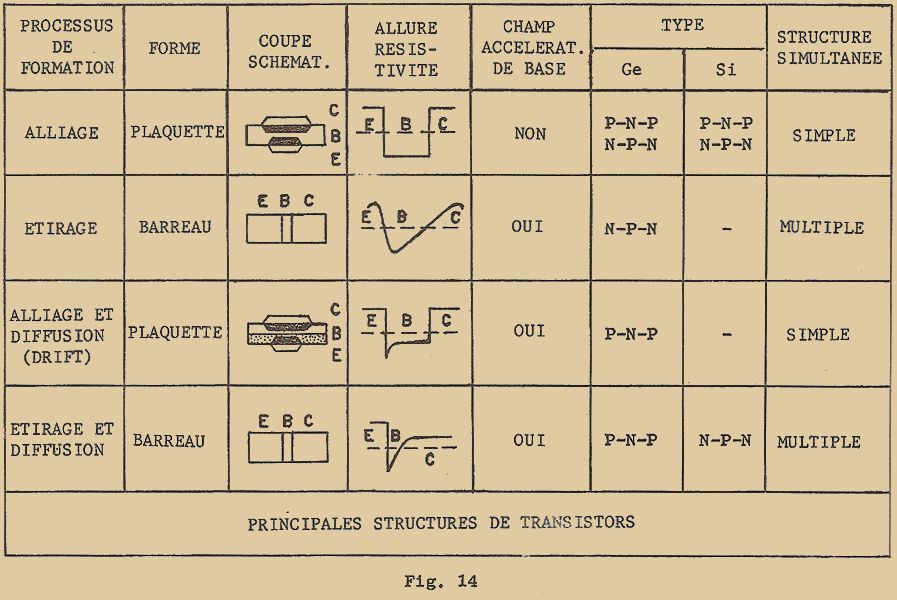
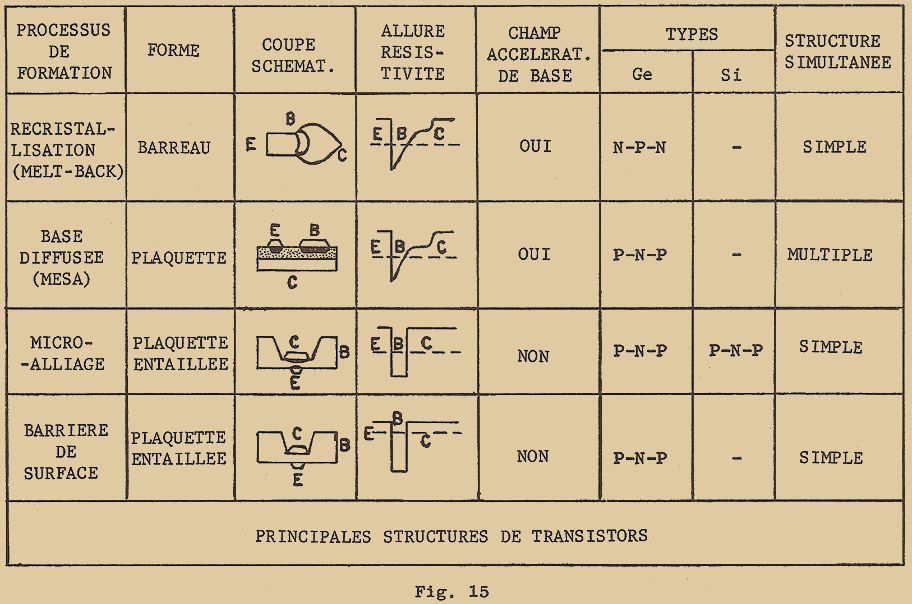
Dans les tableaux des figures 14 et 15, je vous indique les données technologiques des principales structures de transistors obtenus grâce aux techniques fondamentales ou aux techniques mixtes.

Le procédé dit "melt-back", ou de recristallisation, représente une variante du procédé par étirage et diffusion.

Un barreau de monocristal N, dopé par deux éléments d'impuretés un N et un P, chauffé à une extrémité de façon à obtenir la fusion locale du monocristal est ensuite refroidi lentement.

Pendant la recroissance du monocristal il se forme dans la zone centrale une courbe de conductibilité opposée à celle de la zone extrême, et on obtient ainsi une structure de transistor NPN.

Les transistors à micro-alliage et à barrière de surface ont un profil schématique relativement simple, en ce sens que dans l'un comme dans l'autre, l'épaisseur de la base est déterminée par une profonde incision de la plaquette. Le transistor à micro-alliage est une simple variante de celui à alliage, tandis que le transistor à barrière de surface constitue un exemple de la structure que l'on peut obtenir avec une jonction métallique redresseuse par simple soudage des supports d'émetteur et de collecteur sur la plaquette de base.

Dans la dernière leçon théorique, nous passerons en revue les recherches actuelles et l'orientation de la production vers de nouveaux dispositifs à semi-conducteurs. A partir de la prochaine leçon, nous commencerons la troisième partie du cours entièrement consacrée à l'étude des circuits.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 13^ème LEÇON THÉORIQUE

1 – L'extraction du germanium à partir des sous-produits du carbone fossile et du zinc est moins coûteuse ; c'est pour cette raison qu'on la préfère à l'exploitation des minerais de germanium.

2 – Le travail du silicium en vue de son utilisation dans le domaine de l'électronique nécessite des traitements longs et de grandes précautions pour éviter qu'il ne se combine à des éléments étrangers ; ceci détermine le coût élevé de sa production.

3 – De la pureté des semi-conducteurs et de la quantité des impuretés dépendent la régularité du dopage, l'allure de la résistivité du monocristal et en dernier ressort les propriétés électriques du dispositif que l'on se propose de réaliser.

4 – Le coefficient de répartition (ou constante d'isolement) est le rapport entre la concentration des impuretés dans le semi-conducteur recristallisé et la concentration des impuretés dans la zone de fusion mobile.

5 – Dans le travail du silicium, on utilise des fours verticaux, pour pouvoir adopter le procédé de la zone de fusion mobile, avec laquelle on évite l'utilisation d'un creuset ; en effet avec l'utilisation d'un creuset comme celui qui est employé dans les fours horizontaux, on ne peut empêcher le silicium en fusion de se combiner avec le matériau dont est composé le creuset.

6 – Un semi-conducteur polycristallin est formé de nombreux petits cristaux différemment orientés ; les barreaux obtenus à la fin du raffinage sont polycristallins.

7 – Le procédé TCHOKRALSKI permet d'obtenir des zones alternativement P et N.

8 – Le contrôle de la résistivité permet de délimiter le tronçon du barreau que l'on utilisera dans les travaux ultérieurs.

9 – La coupe transversale du monocristal permet d'obtenir des plaquettes où la répartition des impuretés est uniforme et la résistivité reste ainsi constante.

---

EXERCICES DE RÉVISION SUR LA 14^ème LEÇON THÉORIQUE

1 – Quelles sont les techniques fondamentales utilisées pour obtenir des jonctions redresseuses ?

2 – Quel est le processus de formation d'une jonction alliée (ou à alliage) ?

3 – Comment sont branchés les supports des diodes au silicium à jonction par diffusion ?

4 – Pourquoi certains types de transistors de puissance (supérieure à 1 W) ont-ils l'électrode du collecteur reliée à la masse métallique de l'enveloppe ?

5 – Est-ce que le coefficient d'amplification β dépend de l'exécution du montage d'un transistor ?

6 – Comment peut-on diminuer le temps de transit des charges dans l'électrode de base ?

7 – Comment se forme le champ accélérateur dans l'électrode de base ?

8 – Quelle est la signification du nom transistor Mesa ?

9 – A partir du profil de la résistivité de la base peut-on reconnaître s'il y a formation dans le transistor d'un champ accélérateur ?

Fin de la leçon 14

---

LECON 15

1 – CIRCUITS A TRANSISTORS

Avec la présente leçon, nous commencerons la troisième partie du cours, dans laquelle nous examinerons les différents circuits à transistors et étudierons les applications des semi-conducteurs dans la radio en particulier et dans l'électronique en général.

Un circuit quelconque à transistors exploite la propriété amplificatrice d'un tel dispositif, que l'on a largement étudiée en son temps : il est donc parfaitement logique de commencer par le circuit amplificateur qui est le circuit le plus simple à transistors.

Nous avons déjà vu qu'un transistor pour fonctionner correctement devait être polarisé dans des conditions déterminées et qu'il devait travailler en un point défini de ses caractéristiques de collecteur. Nous avons aussi traité longuement des circuits de polarisation, et avons pris en considération les inconvénients qui pouvaient se produire dans certains cas avec l'augmentation de la température et les remèdes que l'on pouvait apporter.

Nous nous proposons d'étudier maintenant, comment un transistor monté dans un circuit, peut amplifier un signal quelconque appliqué à son électrode de commande et comment un tel signal amplifié peut être prélevé de cet étage pour être utilisé dans d'autres circuits.

Suivant les exigences particulières et les types de transistors utilisés on peut obtenir un nombre illimité de circuits amplificateurs différents, mais leur fonctionnement de base reste établi toujours sur le même principe.

Il est donc normal de considérer tout d'abord le circuit amplificateur le plus simple et d'en étudier le fonctionnement et les propriétés avant d'examiner d'autres types d'amplificateurs utilisés dans la technique radio.

Pour étudier un circuit amplificateur, il est nécessaire d'appliquer à ses bornes "d'entrée" un signal et voir comment il se comporte dans ces conditions. L'étude est nettement facilitée, tant au point de vue description du fonctionnement, que des formules qui en découlent si l'on considère non pas un signal quelconque, mais un signal sinusoïdal c'est-à-dire une tension ou un courant dont la valeur varie selon une "loi sinusoïdale".

Le choix d'un tel type de signal est dû au simple fait que la loi sinusoïdale, apparemment bizarre, est en réalité une loi "naturelle". Il suffit de penser que le mouvement d'un pendule obéit à la loi sinusoïdale, ainsi qu'un mouvement oscillant simple quelconque, comme par exemple la vibration de la corde d'un instrument musical. Avant d'examiner le circuit amplificateur il est donc nécessaire de rappeler pour mémoire les propriétés d'une tension ou d'un courant sinusoïdal.

Je vous ai représenté à la figure 1-a, l'allure d'une tension sinusoïdale (ceci reste vrai aussi pour un courant sinusoïdal) : comme vous pouvez le voir, la valeur de la tension part de zéro, augmente jusqu'à atteindre une valeur maximum positive (c'est-à-dire au-dessus de l'axe de référence) indiquée par + Vmax ; puis, elle redescend jusqu'à zéro, et continue à augmenter en dessous de l'axe jusqu'à atteindre la valeur maximum négative, indiquée par – Vmax ; et enfin elle croît à nouveau pour atteindre la valeur zéro ; le cycle est ainsi terminé et peut recommencer à nouveau.

Le temps nécessaire pour effectuer un cycle complet est appelé PERIODE et qui est indiqué en général par la lettre majuscule T ; le nombre de cycles qui s'effectuent dans une seconde (c'est-à-dire dans l'unité de temps) exprime la fréquence de la tension sinusoïdale, indiquée normalement par la lettre f.

La période T et la fréquence f sont liées par la formule simple :

T = 1/f ou f = 1/T

où la période et la fréquence sont exprimées respectivement en secondes (s) et en hertz (Hz) ou bien en millisecondes (ms) et en kilohertz (kHz), ou encore en microsecondes (µS) et en mégahertz (MHz).

Si comme indiqué sur la figure 1, la période est de 20ms = 0,020s, la fréquence sera égale à 1⁄0,02 = 50Hz. Dire en effet que la fréquence est de 50Hz signifie qu'en 1 seconde, on a 50 oscillations complètes, et que la durée d'une seule oscillation est de 1/50 de seconde, soit précisément 20ms.

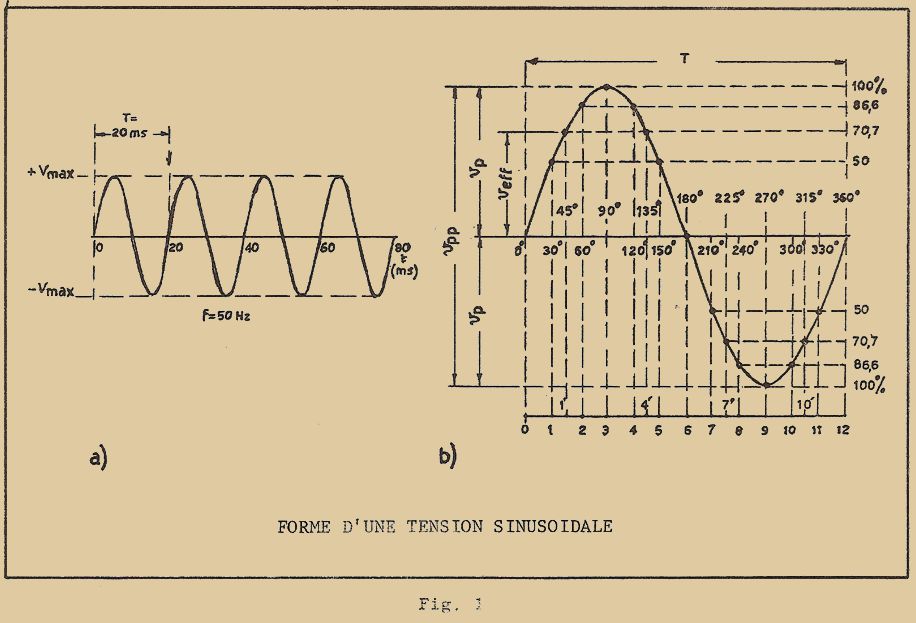
Pour définir une grandeur sinusoïdale, c'est-à-dire une tension ou un courant sinusoïdal, il ne suffit pas de donner sa fréquence ou sa période, mais il faut encore indiquer la valeur de l'amplitude de l'oscillation et ceci peut être fait de différentes façons.

En effet, comme on peut le voir d'après la figure 1-b, l'allure sinusoïdale est parfaitement définie du point de vue mathématiques, de sorte que, après avoir fixé la longueur de la période et après l'avoir partagée en douze parties égales, on peut dessiner la courbe (appelée sinusoïde), parce que l'on sait qu'elle coupe l'axe zéro au point 0 (début de la période), au point 6 (moitié de la période) et au point 12 (fin de la période) ; on sait d'autre part, qu'elle atteint la valeur positive maximum au point 3 (quart de période) et la valeur négative maximum au point 9 (trois quarts de période), ces deux maxima ayant toujours même amplitude.

Aux points 1, 5, 7 et 11, la valeur atteinte est exactement la moitié de la valeur maximum (50%) ; aux points2, 4, 8 et 10, elle est égale à 86,6% (c'est-à-dire √3⁄2) de la grandeur maximum ; enfin aux points 1', 4', 7' et 10' la valeur atteinte est égale à 70,7% (c'est-à-dire √2⁄2) de la valeur maximum

Mathématiquement parlant, la période T est divisée en "360 degrés électriques" et chacune des 12 parties est donc égale à 30° : la correspondance entre les points considérés et les degrés électriques correspondants est évidente d'après la figure même.

Il suffira donc d'indiquer une de ces valeurs pour pouvoir dessiner complètement la sinusoïde. Les plus importantes de ces valeurs pour leur application immédiate dans les calculs, sont la valeur maximum et la valeur efficace. La première est très importante pour pouvoir travailler sur les caractéristiques du transistor comme nous le verrons sous peu. La seconde au contraire est importante pour le calcul de la puissance d'un courant alternatif et elle est la valeur que par convention on utilise pour exprimer "l'amplitude" d'une grandeur sinusoïdale. Une autre valeur très importante est celle que l'on appelle "de crête à crête".

Ces valeurs seront indiquées désormais par V_p (valeur maximum, ou valeur de crête ou valeur de "pic"), Veff (valeur efficace) et V_pp (valeur de crête à crête ; en anglais "peak to peak") (figure 1-b).

Ces valeurs sont liées entr'elles par les relations simples suivantes :

vp = 1,41 x veff		vp = 0,5 vpp
veff = 0,707 x vp		veff = 0,353 x vpp
vpp = 2 x vp		vpp = 2,82 x veff

Après avoir rappelé ces notions sur les grandeurs sinusoïdales, nous pouvons passer directement à l'étude des étages amplificateurs.

1 – 1 AMPLIFICATEURS A TRANSISTORS

Comme nous l'avons dit précédemment, le circuit le plus utilisé en pratique est celui de l'émetteur commun, c'est pour cette raison que ce circuit sera examiné en premier lieu. Bien que le montage en émetteur commun nécessite toujours la stabilisation thermique, pour simplifier le problème nous examinerons d'abord un circuit non stabilisé. Le circuit stabilisé sera étudié en second lieu.

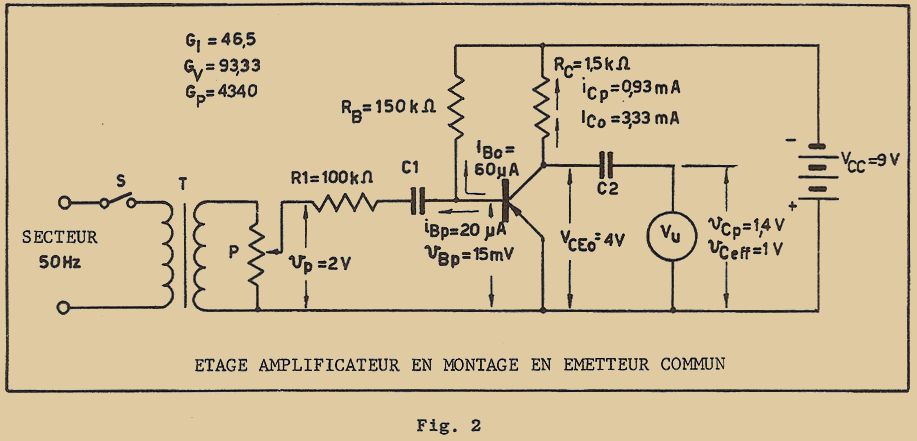
Le schéma le plus simple d'un amplificateur à émetteur commun est représenté à la figure 2. Le transistor est alimenté par la pile de 9 V à travers la résistance de charge R_C de 1,5kΩ et la résistance de polarisation R_B de 150kΩ. Afin de stabiliser le point de fonctionnement, il faut remarquer que les condensateurs C₁ et C₂, branchés respectivement à la base et au collecteur ne laissent pas passer le courant continu (les deux armatures des condensateurs sont en effet isolées entr'elles), ce qui signifie que le reste du circuit n'intervient pas.

Si l'interrupteur S est ouvert, aucune tension alternative n'est appliquée au secondaire du transformateur T, c'est-à-dire à la base du transistor ; dans ces conditions, le point de fonctionnement est déterminé comme nous l'avons vu dans les précédentes leçons.

En considérant les caractéristiques de collecteur (quadrant I de la figure 3) et en traçant la droite de charge, le point de fonctionnement est en A' avec un courant de polarisation de la base de (9 V)⁄(150kΩ) = 0,060mA = 60µA. Le point de fonctionnement appelé encore point de repos, parce qu'il représente le fonctionnement du transistor lorsque l'on n'applique aucun signal à sa base peut encore être reporté dans le quadrant II sur la caractéristique dynamique mutuelle déterminée à partir de la droite de charge du premier quadrant, comme nous l'avons vu en son temps, et dans le quadrant III sur la caractéristique dynamique d'entrée, qui en pratique coïncide avec la courbe donnée dans les catalogues (la seule en général d'ailleurs) et qui correspond souvent à la tension de collecteur de 4,5 V (voir leçons précédentes). On obtient ainsi les points A (quadrant II) et A'' (quadrant III) de la figure 3.

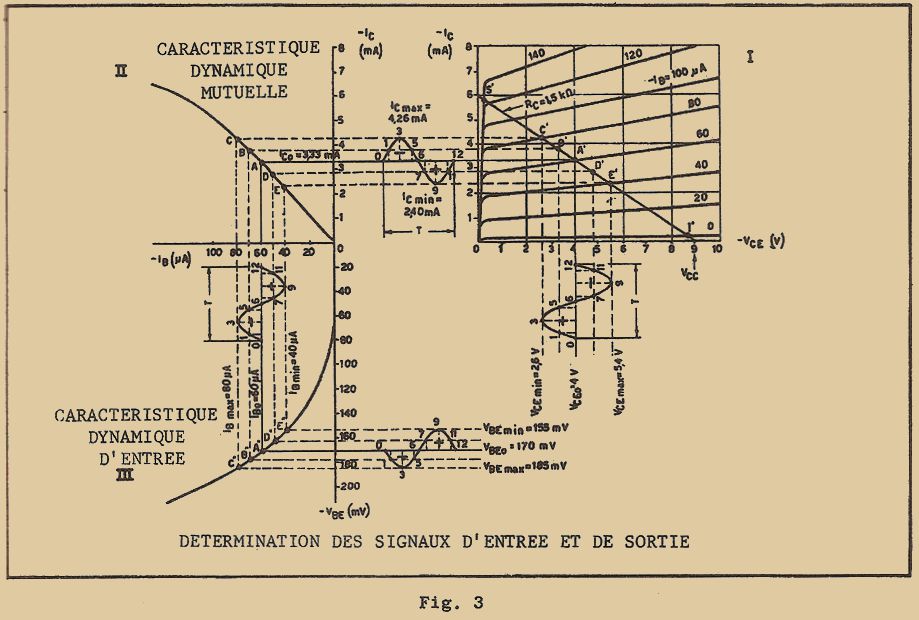
Les courants et les tensions relatifs au point de repos du transistor se déterminent facilement sur la même figure 3 ; on a ainsi :

V_CEo = 4 V ; I_Co = 3,33mA ; I_Bo = 60µA ; V_BEo = 170mV.

Remarquez que l'indice de chaque grandeur est suivi par zéro (o) pour bien indiquer qu'il s'agit de valeurs relatives au point de repos.

Il faut remarquer encore que, tant que S reste ouvert, dans le circuit ne circulent que des courants et tensions continus de polarisation et que le voltmètre Vu branché à la sortie du collecteur par l'intermédiaire de C₂ n'indique aucune tension, puisque C₂ ne laisse pas passer le courant continu.

Fermons maintenant l'interrupteur S et relions le primaire du transformateur T à un générateur de tension alternative, par exemple le réseau de distribution de l'énergie électrique, qui délivre une tension sinusoïdale de 50 Hz.

La tension au secondaire est réglée à la valeur désirée par l'intermédiaire du potentiomètre P et appliquée au transistor à travers la résistance R₁ de 100kΩ et le condensateur C₁, dont la réactance à la fréquence du signal appliqué est supposée faible et peut être négligée devant les 100kΩ de la résistance R₁

De cette manière, on peut considérer que le condensateur C₁ est un simple élément de liaison qui laisse passer totalement le signal alternatif et bloque par contre le courant continu de polarisation en l'empêchant d'aller se refermer à la masse par le potentiomètre P.

Réglons maintenant P de façon à ce que la tension appliquée à R₁ ait une valeur de crête v_p de 2 V (la valeur positive atteinte par le signal est de 2 V, ainsi que la valeur négative maximum).

Cette tension va provoquer un courant dans le circuit constitué par R₁, C₁, et par la jonction base-émetteur (figure 2) et dont la valeur sera pratiquement déterminée par la seule valeur de R₁, car comme nous l'avons dit, on suppose que la réactance de C₁ est négligeable devant R₁ et que d'autre part, la résistance d'entrée du transistor en courant alternatif a une valeur très faible devant les 100kΩ de R₁.

Avec une bonne approximation, on peut dire que la tension v_p va faire circuler dans le circuit, un courant de :

i_Bp = v_p⁄R₁= (2 V)⁄(100kΩ) = 0,02mA = 20µA.

Pendant l'alternance négative, le courant i_Bp a le sens indiqué sur la figure 2, c'est-à-dire le même sens que le courant de polarisation I_Bo. Les deux courants de base vont donc s'ajouter et le courant total de base, aura lors de la crête négative la valeur :

I_Bmax = I_Bo + i_Bp = 60 + 20 = 80µA.

Pendant l'alternance positive, le courant i_Bp sera dans le sens opposé à celui indiqué sur la figure 2, c'est-à-dire qu'il sera de sens opposé au courant de polarisation. Le courant de base sera donc égal à la différence des deux courants et pendant la crête de l'alternance positive atteindra la valeur :

I_Bmin = I_Bo - i_Bp = 60 - 20 = 40µA.

En conclusion donc, si l'on applique un signal sur la base d'un transistor, le courant total de base va résulter de la superposition d'un courant continu de polarisation I_Bo et du courant alternatif i_B du signal, c'est-à-dire qu'il sera variable dans le temps comme le signal lui-même. Dans le cas de l'exemple le courant total de base va varier continuellement entre 80µA et 40µA en suivant l'allure sinusoïdale puisque l'on a supposé que c'était l'allure du signal appliqué sur la base.

Pour étudier le comportement du transistor dans ces conditions, il faut opérer sur les caractéristiques de la figure 3 en faisant quelques constructions graphiques simples.

Considérons la droite verticale qui passe par le point de fonctionnement A du deuxième quadrant et sur cet axe, prenons un segment de longueur quelconque, par exemple celui qui est limité sur la figure par les points 0 et 12.

Ce segment correspond à une période du signal sinusoïdal appliqué sur la base. Traçons dessus la sinusoïde qui le représente, selon la construction indiquée sur la figure 1-b.

Pour simplifier le dessin nous ne considérerons seulement que les points 0, 6 et 12 qui se trouvent sur l'axe, les points 3 et 9 qui représentent les crêtes et les points 1, 5, 7 et 11, où la sinusoïde atteint une valeur égale à la moitié du maximum. Comme dans le cas de l'exemple, la valeur de i_Bp est de 20µA, l'amplitude maximum de la sinusoïde sera donc de 20µA.

En reportant les points de la sinusoïde sur l'axe horizontal à l'aide de droites parallèles passant par ces points (lignes en pointillés sur la figure) on pourra lire sur cet axe les valeurs du courant de base correspondant à chacun des points considérés sur la sinusoïde.

On peut ainsi voir, qu'en partant de 60µA (point 0), le courant croît à 70µA (point 1), puis à 80µA (point 3), puis redescend à 70µA (point 5) et redevient 60µA, (point 6) en terminant ainsi la première alternance. Pendant l'autre alternance, le courant de base continue à diminuer jusqu'à 50µA (point 7), puis passe par la valeur minimum de 40µA (point 9) et recommence ensuite à augmenter à 50µA (point 11) pour reprendre la valeur de 60µA (point 12) terminant ainsi le cycle complet.

Nous avons donc vu que pendant les deux alternances (une période) le courant de base part de sa valeur de repos, augmente de 20µA (c'est-à-dire d'une valeur égale à la valeur de la crête de la sinusoïde qui représente le signal d'entrée) atteignant la valeur maximum I_Bmax de 80µA, puis diminue jusqu'à atteindre la valeur minimum I_Bmin de 40µA et accomplit ainsi une excursion totale égale à la différence entre la valeur maximum et la valeur minimum, qui dans le cas de l'exemple est égale à I_Bmax – I_Bmin = 80 – 40µA

Cette valeur est égale à celle de crête à crête du signal appliqué à la base, c'est-à-dire i_Bpp = 2 x i_Bp = 2 x 20 = 40µA

L'excursion du courant de base peut être suivie sur la caractéristique dynamique mutuelle du deuxième quadrant, en observant comment se déplace le point de fonctionnement du transistor pendant le cycle du signal d'entrée. Pour cela, il suffit de prolonger les lignes en pointillés jusqu'à rencontrer la caractéristique même.

On voit ainsi que le point de fonctionnement se déplace de A jusqu'au point C, puis revient en arrière jusqu'au point E et retourne au point de départ A après avoir effectué un cycle complet. L'excursion du point de fonctionnement sur la caractéristique dynamique mutuelle est ainsi représentée par la portion de la courbe comprise entre C et E.

Il est facile maintenant de représenter l'allure du courant de collecteur, puisque la caractéristique dynamique mutuelle a précisément le rôle de passer des valeurs du courant de base à celles du courant de collecteur correspondant.

La construction se fait de la façon suivante. A partir du point A, on trace une droite horizontale qui passant justement en A, représente l'axe du signal de sortie, c'est-à-dire du courant de collecteur. Sur cette droite, on prend un segment de longueur égale à celle prise précédemment sur l'axe vertical passant par le point A et représentant la période T. Ce segment sera encore partagé en 12 parties égales numérotées par les points correspondants de 0 à 12 en mettant pour simplifier les points 2, 4, 8 et 10.

Si nous traçons maintenant les lignes horizontales parallèles qui passent par les différents points de fonctionnement considérés sur la caractéristique dynamique, nous déterminerons les points correspondants qui donnent l'allure du courant de collecteur. En effet, quand le point de fonctionnement se trouve en A, nous avons le point 0 ; quand le point vient en B et en C nous venons en 1 et 3 ; c'est en 3 que le courant de collecteur atteint sa valeur la plus élevée. Ensuite le point de fonctionnement redescend en B, en A, puis en D, et arrive enfin au point E : le courant de collecteur diminue en 5, 6, 7 et atteint sa valeur minimum en 9. Puis le point de fonctionnement remonte de D et revient en A, tandis que le courant de collecteur passe aux points 11 et 12.

Comme il apparait sur la figure 3, l'allure du courant de collecteur est encore sinusoïde, comme l'est le courant de base. Pendant le cycle, le courant de collecteur passe de sa valeur de repos I_Co = 3,33mA à la valeur maximum I_Cmax = 4,26mA (point 3), puis redescend à la valeur à la valeur minimum I_Cmin = 2,40mA (point 9).

Si l'on se rappelle qu'avec la construction ainsi effectuée, on obtient une correspondance parfaite entre le numérotage des points de la sinusoïde représentant le courant de base avec ceux de la sinusoïde représentant le courant de collecteur, on en déduit que lorsque le courant de base augmente, le courant de collecteur augmente aussi et inversement lorsque le premier diminue, le second suit le mouvement ; ceci exprime que le courant de sortie (collecteur) est en phase avec le courant d'entrée (base).

Comme on l'a vu, le courant de base est variable, car il est constitué par le courant de repos I_Bo auquel se superpose le courant alternatif (sinusoïdal) i_B du signal d'entrée. De la même façon, le courant variable du collecteur peut être considéré comme résultant du courant continu de repos I_Co, auquel se superpose le courant alternatif i_C provoqué par le signal appliqué.

Le courant continu I_Co prend le nom de Composante Continue du courant de collecteur, tandis que le courant alternatif i_C qui se superpose, prend le nom de Composante Alternative. C'est cette dernière composante qui représente le signal de sortie de l'amplificateur.

L'amplitude du courant du signal de sortie peut facilement être déterminée, à partir du moment où la valeur de crête à crête de la sinusoïde est donnée exactement par l'excursion du courant collecteur et où la valeur de crête est égale à la moitié de la valeur précédente.

Ainsi, dans le cas de l'exemple, on a :

i_Cpp = I_Cmax – I_Cmin = 4,26 -2,40 = 1,86mA

et que :

i_Cp =i_Cpp⁄2 = 1,86 : 2 = 0,93mA

Le même raisonnement peut être repris en ce qui concerne la tension de collecteur, dont l'allure peut se déduire de celle du courant de collecteur par une construction analogue. Il suffit en effet de reporter les points de fonctionnement A, B, C, D, E, du quadrant II sur la droite de charge du quadrant I, déterminant ainsi les points A', B', C', D', E', et de considérer comme axe de référence, la verticale qui passe par le point de repos qui est maintenant A'.

L'allure de la tension de collecteur est encore sinusoïdale comme on peut le voir sur la figure 3, et les valeurs de la tension doivent être lues sur la même horizontale que celle qui correspond aux tensions du collecteur. On voit ainsi que la tension de collecteur, dont la valeur de repos V_CEo est de 4 V, atteint la valeur maximum V_CEmax de 5,4 V (point 9) et la valeur minimum V_CEmin de 2,6 V ; elle accomplit une excursion égale à V_CEmax– V_CEmin = 5,4 – 2,6 = 2,8 V.

On peut considérer ainsi que la tension de collecteur est la résultante d'une composante continue, constituée par la tension continue de repos V_CEo, et d'une composante alternative v_C qui représente le véritable signal de sortie (ou de tension). La valeur de crête à crête de v_C est donnée par l'excursion de la tension de collecteur et est égale dans notre exemple à 2,8 V, tandis que la valeur de crête est égale à la moitié de cette valeur soit 1,4 V.

Il faut remarquer encore que quand le courant de base (signal d'entrée) atteint sa valeur maximum (point 3), la tension de collecteur atteint sa valeur minimum et inversement, lorsqu'il atteint sa valeur minimum (point 9), la tension atteint sa valeur maximum. Pour cette raison, on dit que le courant d'entrée et la tension de sortie sont en opposition de phase, ou ce qui revient au même, sont déphasés de 180°.

La tension de sortie de l'amplificateur est mesurée par le voltmètre pour le courant alternatif indiqué par Vu sur la figure 2.

Il est relié au collecteur par l'intermédiaire du condensateur C₂ qui permet d'appliquer au voltmètre la seule composante alternative de la tension du collecteur.

Si le voltmètre est gradué en valeur efficace, comme il l'est en général, la valeur indiquée sera celle de crête divisée par 1,41 ; on lira ainsi sur le voltmètre, la valeur :

v_Ceff = v_Cp⁄1,41 = 1,41 : 1,41 = 1 V environ

Il nous reste encore à déterminer l'allure de la tension qui s'établit entre la base et l'émetteur. Pour cela, il faut reprendre la caractéristique dynamique d'entrée du quadrant III et y porter les points de fonctionnement A'', B'', C'', D'', E'', pour déterminer l'allure de la tension V_BE dont les valeurs peuvent être lues sur l'axe vertical gradué en mV.

On voit ainsi que l'allure de la tension de base est encore sinusoïdale ; la tension de base passe pendant le cycle, de la valeur de repos V_BEo de 170mV à la valeur maximum V_BEmax de 185mV et à la valeur minimum V_BEmin de 155mV et accomplit une excursion de 185 – 155 = 30mV.

La tension de base (tension d'entrée) peut aussi être considérée comme étant composée d'une tension continue, égale à la tension de repos V_BEo de 170mV, et d'une composante alternative v_B, dont la valeur de crête à crête v_Bpp est donnée par l'excursion de la tension de base et qui est égale à 30mV, tandis que sa valeur de crête v_Bpp est égale à v_Bpp : 2 , soit 30 : 2= 15mV

Si l'on examine la figure 3, on peut voir que lorsque le courant de base atteint sa valeur maximum (point 3) la tension de base atteint aussi sa valeur maximum. On en déduit alors que le courant et la tension d'entrée sont en phase. Sur la même figure, on voit que la tension d'entrée et celle de sortie sont en opposition de phase : le courant et la tension de sortie sont donc aussi en opposition de phase.

1 – 2 GAIN EN COURANT, EN TENSION ET EN PUISSANCE –

Pour un étage amplificateur on peut définir trois gains différents selon que l'on considère les courants, les tensions ou les puissances à l'entrée et à la sortie.

Après avoir fixé l'allure du courant de commande du transistor et déterminé les allures du courant et de la tension de sortie (et même à la rigueur celle de la tension d'entrée), les gains peuvent facilement être calculés si l'on se rappelle comment ils sont définis.

Par gain, on entend le rapport entre l'amplitude du signal de sortie à celle du signal d'entrée), ainsi le gain en courant sera donné par le rapport entre la composante alternative du courant de collecteur et la composante alternative du courant de base.

On peut prendre pour ces courants, indifféremment les valeurs de crête à crête, ou les valeurs de crête, ou les valeurs efficaces pourvu que l'on prenne pour les deux la même valeur. D'après les constructions graphiques de la figure 3, il est très facile de mesurer les excursions totales des courants, et on peut dire que le gain de courant (que nous désignerons par G_I) est donné par la formule :

G_I = (I_Cmax - 〖 I〗_Cmin)/(I_Bmax - I_Bmin)

où les courants doivent être exprimés dans les mêmes unités. Si l'on choisit le microampère par commodité, on aura :

G_I = (4.260-2.400)/(80-40) = 1.860/40 = 46,5

De façon analogue on définit le gain en tension, en prenant cette fois la tension de base et la tension de collecteur. Le gain sera indiqué par G_V et sa valeur donnée par la formule :

G_V = (V_CEmax - 〖 V〗_CEmin)/V_BEmax - V_BEmin)

où les tensions doivent être exprimés dans les mêmes unités. Si l'on choisit le millivolt, on obtient dans l'exemple de la figure 3 :

G_V = (5.400-2.600)/(185-155) = 2.800/30 = 93,33

Le gain de puissance enfin, est donné par le rapport entre la puissance de sortie P_u (puissance d'utilisation) et la puissance d'entrée P_e. Comme les tensions et les courants sont considérés comme sinusoïdaux, la puissance sera donnée par le produit de leurs valeurs efficaces.

Si l'on calcule, à partir des valeurs de courant et de tension maximum et minimum, lues sur la figure 3, on aura :

P_u = v_Ceff x i_Ceff =((V_CEmax - V_CEmin ) x (I_Cmax -I_Cmin))/8

et par analogie :

P_e = v_Beff x i_Beff = =(V_BEmax - V_BEmin ) x (I_Bmax -I_Bmin))/8

La puissance sera donnée en milliwatt (mW) si la tension est exprimée en volt (V) et le courant en milliampère (mA), ou bien en microwatt (µW), si la tension est exprimée en millivolt (mV) et le courant en milliampère (mA).

Dans le cas de notre exemple, si l'on exprime la tension de collecteur en volt et le courant en milliampère :

P_u = ((5,4-2,6) x (4,26-2,40))/8 = (2,8 x 1,86)/8 = 0,651mW

et en exprimant la tension de base en millivolt et le courant de base en milliampère on a

P_e = ((185-155) x (0,08-0,04))/8 = (30 x 0,04)/8 = 0,15µW

Comme 0,651 mW = 651 µW, on peut calculer le gain de puissance G_P qui est alors :

G_P = P_u/P_e  = 651/0,15 = 4.340

On peut aussi vérifier rapidement que le gain de puissance n'est autre que le produit des gains en courant et en tension. En effet :

G_P = G_I x G_V = 46,5 x 93,33 = 4.340 environ

En ce qui concerne les valeurs des gains, on peut donner les précisions suivantes. Le gain en courant est d'autant plus proche du coefficient d'amplification β du transistor (mesuré au point de repos) que plus faible est la valeur de la résistance de charge. Pour R_C = 0 c'est-à-dire lorsque le collecteur est directement relié à la pile, on a exactement G_I = β

Dans ces conditions, on obtient la valeur maximum pour le gain en courant, mais le gain en tension est réduit à zéro. En effet, si le collecteur est relié directement à la pile, la tension du collecteur est constamment égale à la tension V_CC délivrée par la pile et ne subit donc aucune variation lorsque l'on applique un signal à l'entrée.

Ceci signifie donc que la composante alternative de la tension de collecteur est nulle, et que l'on n'a pas de tension à la sortie ; en d'autres termes, le gain en tension est nul : G_V = 0.

De même, le gain en puissance est alors nul, puisqu'il n'y a pas de puissance à la sortie, car v_C = 0.

Pour que le gain en tension ne soit pas nul, il faut que la résistance de charge soit différente de zéro. Plus celle-ci est élevée, plus grand sera G_V, mais par contre plus faible sera la valeur de G_I comme on l'a dit plus haut. En augmentant la valeur de R_C, on augmente le gain en tension, tandis que le gain en courant va en diminuant.

On peut déterminer que le gain en puissance atteint une valeur maximum pour une valeur bien déterminée de R_C, qui est appelée "charge optimum". La charge optimum d'un transistor dépend avant tout du type de transistor et aussi du point de repos choisi. Pour obtenir ainsi le gain maximum de puissance, c'est-à-dire la puissance maximum à la sortie, il faut déterminer avec grand soin la valeur de R_C, ce qui peut se faire en refaisant la construction graphique de la figure 3 pour différentes valeurs de la résistance de charge, jusqu'à ce que l'on ait trouvé la valeur qui convient le mieux.

On trouve alors que le gain maximum est obtenu pour une valeur de R_C à peu près égale à la valeur de la résistance de sortie en courant alternatif du transistor (définie dans la douzième leçon de théorie) et calculée pour le point de repos choisi.

Lorsque l'on ne s'intéresse uniquement qu'au gain en courant ou en tension, on choisit la valeur de R_C ou faible ou grande.

1 – 3 RÉSISTANCE D'ENTRÉE ET DE SORTIE

Ayant défini dans la douzième leçon de théorie une résistance d'entrée et une résistance de sortie en courant alternatif, pour le transistor seul, on peut définir maintenant deux résistances analogues pour l'étage amplificateur complet.

En partant du principe général de la résistance, défini par la loi d'Ohm comme étant le rapport entre la tension appliquée aux bornes de la résistance considérée et le courant qui la traverse, on définit la résistance d'entrée de l'étage amplificateur comme étant le rapport entre la tension alternative que l'on applique à son entrée et le courant qui traverse ce même circuit d'entrée.

Je vous ai redessiné à la figure 4, le schéma de la figure 2, où pour une commodité de raisonnement, j'ai polarisé la base à l'aide d'une pile séparée, ce qui ne modifie en aucune façon le fonctionnement de l'étage.

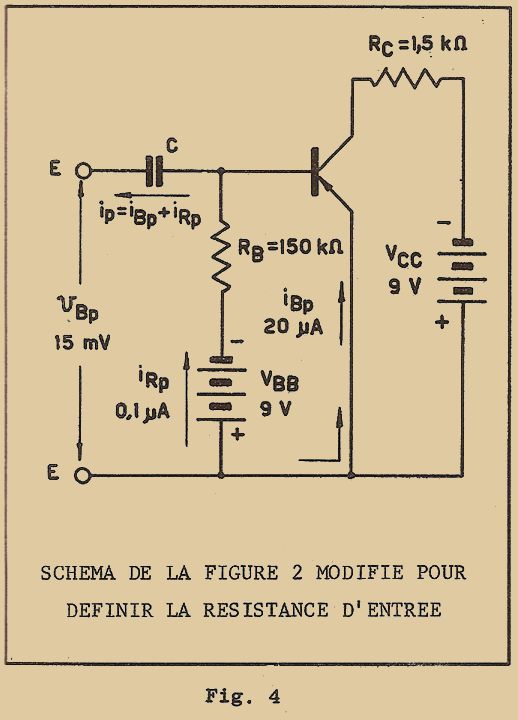
Appliquons maintenant aux bornes d'entrée, c'est-à-dire aux points indiqués EE de la figure 4, la tension alternative considérée auparavant et dont la valeur de crête est v_Bp = 15mV. De cette manière, le courant de crête de base i_Bp sera encore de 20µA puisque les conditions de fonctionnement sont les mêmes que sur la figure 2.

La tension alternative v_Bp, comme on le voit sur la figure 4, est appliquée aussi à la résistance R_B qui, en série avec la pile, se trouve en parallèle sur la base, c'est-à-dire entre la base et la masse, ce qui signifie que la résistance R_B et la pile seront parcourues par le courant alternatif i_Rp. Comme la pile a une résistance très faible, et se comporte pratiquement comme une simple liaison pour le courant alternatif, la valeur du courant sera donnée simplement par :

i_Rp = v_Bp⁄R_B = (15mV)⁄(150kΩ) = 0,1µA

Dans le cas de l'exemple, le courant i_Rp est très faible et peut être complètement négligé devant le courant qui traverse la base, comme on l'a fait sur la figure 2. Nous ne l'avons considéré seulement, que pour bien préciser qu'en général le courant d'entrée d'un étage, n'était pas simplement i_Bp mais qu'il y avait en plus i_Rp.

En conséquence, on en déduit que la résistance d'entrée de l'étage n'est pas simplement la résistance d'entrée du transistor (qui dans le cas de l'exemple est :

r_B = v_Bp⁄i_Bp  = (15mV)⁄(20µA) = 0,75kΩ), mais qu'il y a aussi la résistance R_B en parallèle.

La résistance r_e d'entrée de l'étage est donnée par la formule :

r_e = (r_B x R_B )/(r_B +〖 R〗_B ) = (0,75 x 150)/(0,75+150) = 112,5/150,75 = 0,746kΩ = 746Ω

Comme on le voit, la valeur de r_e diffère très peu de la valeur de r_B (746Ω au lieu de 750Ω) dans le cas de l'exemple pour un montage en émetteur commun et non stabilisé du point de vue thermique. Nous verrons dans d'autres circuits où la valeur de R_B n'est plus aussi grande par rapport à r_B, que la résistance d'entrée de l'étage peut être sensiblement plus faible que celle de la résistance d'entrée du transistor.

A propos de cette dernière, c'est-à-dire r_B, vous devez noter qu'elle aurait pu être calculée à partir des excursions de la tension et du courant de base vus sur la figure 3 et en utilisant la formule suivante :

r_e = V_BEmax - V_BEmin)/(I_Bmax - I_Bmin ) = (185-155)/(80-40) = (30mV)/(40µA) = 0,75kΩ

Dans le cas du montage en émetteur commun, la valeur de r_B est pratiquement égale à celle de la résistance d'entrée en courant alternatif, comme elle a été définie dans la douzième leçon théorique.

De façon analogue on peut déterminer la résistance de sortie de l'étage, qui résulte de la mise en parallèle de la résistance de charge R_C et de la résistance de sortie r_C du collecteur, c'est-à-dire que l'on a :

r_S = (r_C x R_C )/(r_C +〖 R〗_C )

En se rappelant que pour le montage en émetteur commun, la résistance de collecteur r_C est la même pratiquement que la résistance de sortie en courant alternatif du transistor, définie dans la douzième leçon de théorie, on trouve dans le cas de l'exemple de la figure 3, pour le point de repos A', la valeur r_C = 7kΩ environ. La résistance de sortie de l'étage est alors avec R_C = 1,5kΩ.

r_S = (7 x 1,5)/(7+1,5)= 10,5/8,5 = 1,236kΩ

Le calcul des valeurs des résistances d'entrée et de sortie du transistor et de l'étage dans lequel il est monté, a une très grande importance dans l'étude des amplificateurs à plusieurs étages, comme nous le verrons plus tard.

2 – SIGNAL MAXIMUM À L'ENTRÉE ET À LA SORTIE

Dans l'exemple de la figure 2, on a supposé que l'on faisait circuler dans la base, un courant alternatif de 20µA crête, et qu'il était obtenu en appliquant en amont, une tension de 2V crête à une résistance de 100kΩ.

Supposons maintenant que l'on augmente le courant de commande du transistor, c'est-à-dire la valeur de i_Bp, en agissant simplement sur le potentiomètre P de la figure 2, c'est-à-dire sur la valeur de v_p. Nous voulons voir jusqu'à quelles valeurs de i_Bp on peut aller, et comment une telle augmentation se répercute sur les autres tensions et courants.

Les limites extrêmes du point de fonctionnement sur la droite de charge (quadrant I) sont représentées par S' (point de saturation) et I' (point d'interdiction) ; il est évident que la valeur maximum de i_Bp sera celle qui amènera le point de fonctionnement en un de ces deux points.

En reportant sur la figure 5, les différentes caractéristiques déjà considérées à la figure 3, on voit qu'en augmentant i_Bp, le premier des deux points limites atteint est le point I' (interdiction du courant de collecteur) qui correspond à la valeur zéro atteinte par le courant de base (I_Bmin = 0)

Comme le courant de repos est de 60µA, la valeur maximum de i_Bp est donc de 60µA (en effet I_Bmin = I_Bo – i_Bp = 60 – 60 = 0µA).

Par conséquent, la valeur maximum du courant de base est :

I_Bmax = I_Bo + i_Bp = 60 + 60 = 120µA comme on peut le voir clairement sur la figure 5.

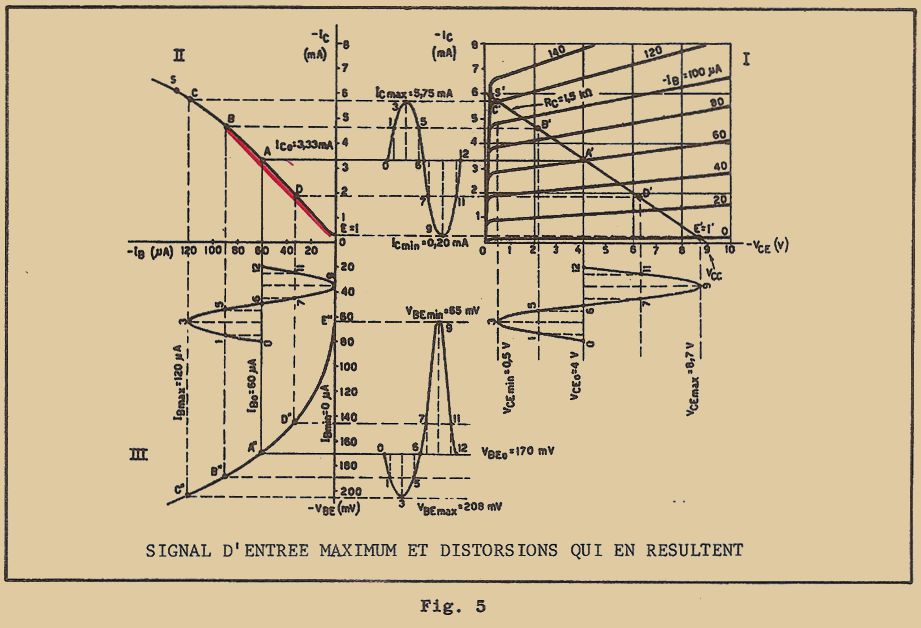
Il suffit maintenant de refaire la construction déjà indiquée à la figure 3 pour obtenir l'allure du courant du collecteur et des tensions du collecteur et de la base.

En examinant la figure 5 on notera que ces tensions sont loin d'être sinusoïdales.

La raison de ceci est que le signal de commande est relativement grand et que la caractéristique dynamique mutuelle (quadrant II) balayée par le point de fonctionnement est limitée maintenant par les points C et E ; comme on peut le voir, elle n'est plus rectiligne, mais bien incurvée.

Quand le courant de base passe de la valeur de repos (60µA) à la valeur maximum (120µA), le point de fonctionnement se déplace de A en C et le courant de collecteur passe de 3,33mA à 5,75mA et subit ainsi une augmentation de 5,75 – 3,33 = 2,42mA. Lorsqu'inversement le courant de base passe de 60µA à 0, le point de fonctionnement se déplace de A en E et le courant de collecteur subit une diminution de 3,33mA à 0,20mA, c'est-à-dire 3,33 – 0,20 = 3,13mA. Les deux alternances du courant de collecteur sont donc inégales, ce qui signifie que le courant de sortie de l'amplificateur est DISTORDU.

Si l'on passe maintenant de la forme du courant à celle de la tension de collecteur, on notera qu'elles sont parfaitement identiques (comme formes naturellement, puisque les amplitudes peuvent être différentes) ; ceci est dû au fait que le passage se fait par l'intermédiaire de la droite de charge et que par sa nature même, celle-ci est parfaitement linéaire.

Si l'on passe à la détermination de la forme de la tension de base on trouve une différence encore plus marquée entre les deux alternances de celle-ci, car la caractéristique dynamique d'entrée du quadrant III est beaucoup plus incurvée que la caractéristique mutuelle du quadrant II.

En conclusion si l'on augmente le signal d'entrée, on augmente aussi le signal à la sortie, mais à cause de la courbure inévitable de la caractéristique dynamique des quadrants II et III dûe à la nature même du transistor, le signal à la sortie sera de plus en plus déformé.

Si l'amplificateur doit amplifier un signal phonique (BF) il est évident que la déformation, c'est-à-dire la distorsion du signal de sortie ne pourra être tolérée que jusqu'à un certain point.

Pour cette raison, l'amplitude maximum du signal d'entrée, et ainsi du signal de sortie, est limitée presque toujours par la distorsion maximum admise, et non pas par les deux points de saturation et d'interdiction, qui représentent les points limites que peut atteindre le point de fonctionnement.

Pour obtenir l'amplitude maximum du signal de sortie avec une distorsion minimum, il faut choisir convenablement la tension d'alimentation V_CC et la valeur de la résistance de charge R_C, de façon à obtenir une caractéristique dynamique mutuelle la plus droite possible. Il faut ensuite déterminer sur celle-ci le point de repos de façon à pouvoir balayer au maximum cette courbe pratiquement linéaire, en ayant soin d'éviter que le point de fonctionnement n'atteigne la partie supérieure où la courbe commence à s'incurver. Ceci signifie que dans le cas de la figure 5, il faut limiter l'excursion du point de fonctionnement à la partie E-B, et fixer le point de repos vers le milieu de celle-ci.

3 – COMMANDE EN COURANT ET EN TENSION

Dans le cas de la figure 3 et de la figure 5, le transistor est commandé par un certain courant de base, imposé par le schéma de la figure 2.

En effet, le courant du signal de la base est défini par la résistance de forte valeur (100kΩ) placée en série avec la liaison de la base, et a donc ainsi la même forme sinusoïdale que la tension v_p appliquée en amont de la résistance R₁.

Si le signal appliqué est de forte amplitude (figure 5) de façon à balayer une grande partie de la caractéristique d'entrée du quadrant III, la tension V_BE aura une forme fortement distordue, mais qui n'a pas d'effet sur la forme du courant et de la tension de sortie, parce que le courant de base reste toujours sinusoïdal. C'est pour cette raison, que l'on dit que le transistor est commandé en courant, parce que c'est la forme du courant de base qui est imposée par le circuit extérieur.

Le transistor peut aussi être commandé d'une autre façon, en appliquant par exemple directement la tension de commande entre la base et la masse, comme indiqué sur la figure 6. L'amplitude de la tension de commande v_Bp peut encore être réglée par le potentiomètre P, dont la valeur ohmique devra être très faible car la tension v_p appliquée à ses bornes est très faible (de l'ordre de quelques dixièmes se volts).

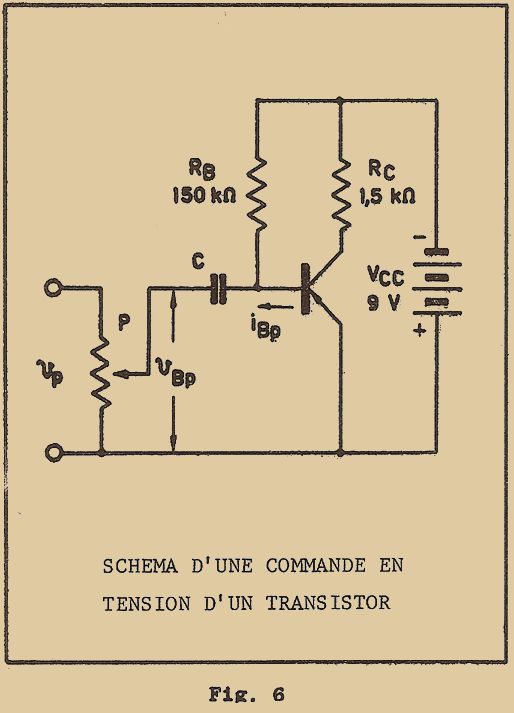
De cette façon, on impose la forme de la tension de base, et la forme du courant de base sera déterminée par la caractéristique d'entrée correspondante : on dira alors que le transistor est commandé en tension.

Si le signal appliqué n'est pas de grande amplitude et qu'ainsi on puisse considérer que la partie de la caractéristique d'entrée est rectiligne (comme c'est le cas dans l'exemple de la figure 3) les commandes en courant et en tension sont équivalentes ; en effet, faire circuler un courant i_Bp de 20µA ou appliquer une tension v_Bp de 15mV conduit au même résultat final, comme on peut le voir clairement sur la même figure 3.

Quand le signal d'entrée est de forte amplitude, les deux types de commandes ne sont plus équivalents car c'est maintenant le courant au lieu que ce soit la tension de la base qui garde la forme sinusoïdale. La figure 5 illustre clairement ce qui arrive lorsque le transistor est commandé en courant ; la figue 7 illustre par contre le cas, où il est commandé par une tension.

Supposons que l'on applique sur la base, une tension v_Bp de 40mV ; la sinusoïde qui représente la forme de la tension de commande sera alors construite en prenant comme axe de référence, la droite horizontale qui passe par la valeur de la tension de repos de la base V_BEo = 170mV.

Comme on peut le voir sur la figure 7, l'excursion de la tension de la base est délimitée par des valeurs V_BEmax = 210mV et V_BEmin = 130mV et par simple construction on peut passer à la détermination de la forme du courant de base par l'intermédiaire de la caractéristique d'entrée.

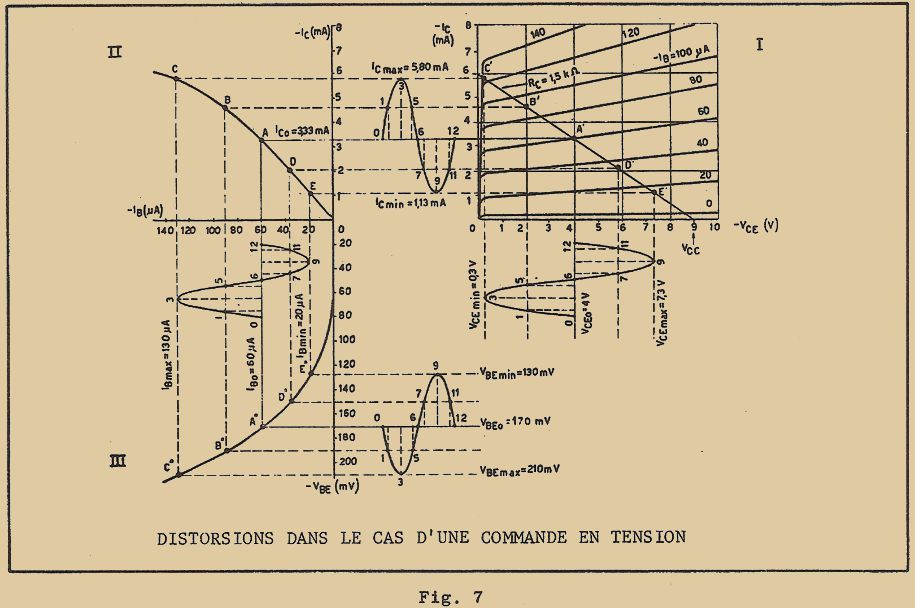
En examinant la figure 7, on remarquera comment maintenant (commande du transistor en tension) le courant de base a une forme assez distordue. En effet les deux alternances de I_B sont différentes : accroissement du courant de base de l'ordre de 70µA contre une diminution de 40µA seulement.

Par contre, cette distorsion n'est pas du tout gênante, car elle est compensée partiellement par la courbure de la caractéristique mutuelle du deuxième quadrant. Si l'on trace en effet l'allure du courant de collecteur qui en résulte, on voit que ce dernier se rapproche de la sinusoïde ainsi que la tension du collecteur.

Ceci est dû au fait que les courbures des deux caractéristiques sont telles qu'elles se compensent en partie ; ainsi, en commandant le transistor en tension dans des conditions déterminées, on peut obtenir un signal de sortie moins distordu.

Les deux types de commande que nous venons de voir sont deux cas théoriques extrêmes qui en pratique ne sont jamais atteints. En effet, dans le cas de la figure 2, il n'est vrai qu'en première approximation que le courant de base est défini exclusivement par R₁ : en réalité, en série avec R₁, se trouve la résistance d'entrée du transistor dont la valeur n'est pas constante pendant tout le cycle ; pour cette raison la forme du courant de base se "ressent" plus ou moins de la présence du transistor, c'est-à-dire de la courbure de la caractéristique d'entrée. En d'autres termes, le courant de base résultant n'est pas parfaitement sinusoïdal comme on l'a supposé dans l'exemple.

Dans le cas de la figure 6, la présence du potentiomètre en série avec la résistance d'entrée du transistor, modifie aussi légèrement la caractéristique d'entrée et ainsi la forme de la tension de la base se "ressentira" plus ou moins de la forme du courant de base absorbé par le transistor et ne sera pas parfaitement sinusoïdale.

En pratique donc, ces deux types de commande ne sont réalisés qu'avec une certaine approximation, mais sont très utiles pour simplifier l'étude des circuits réels.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 14^ème LEÇON THÉORIQUE

1 – La technique de la jonction métallique (à pointe ou soudée), celle de la jonction par alliage, des jonctions par étirage et par diffusion.

2 – On fond le matériau d'impuretés et dans la masse en fusion on dissout une partie du semi-conducteur dont est formée la plaquette, c'est-à-dire la région superficielle qui est en contact avec le liquide ; ensuite, par un lent refroidissement, on obtient la recristallisation du semi-conducteur sur la structure originelle de la plaquette ; la couche recristallisée contient surtout les nouvelles impuretés qui sont du type opposé à celles qui étaient à l'origine dans la plaquette et forme ainsi dans la plaquette même une jonction P-N.

3 – Le support de cathode vient à être relié à la couche N par le procédé de la thermocompression ; le support d'anode est simplement soudé sur la couche P, qui a été traitée auparavant par une diffusion superficielle de bore.

4 – Car on améliore ainsi la dissipation thermique du transistor.

5 – Oui ; une variation dans le traitement qui précède la fermeture du transistor peut faire diminuer la valeur du coefficient β.

6 – En réduisant l'épaisseur de la base, ou bien en accélérant ces charges mêmes par formation d'un champ électrique local.

7 – Par diffusion des charges mobiles, lorsque l'on a établi auparavant un gradient d'impuretés dans l'électrode de base.

8 – Parce que le profil de ces transistors rappelle celui des de deux montagnes de forme conique ; on donne à ces montagnes d'Amérique du Sud, le nom de "Mesa".

9 – Oui. Si la résistivité dans l'électrode de base est constante il n'y a pas de champ accélérateur (interne) ; dans le cas contraire, on a formation d'un champ le long de la région où il y a un gradient d'impuretés et où la résistivité croît au lieu de décroître.

---

EXERCICES DE RÉVISION SUR LA 15^ème LEÇON THÉORIQUE

1 – A quelle fréquence, correspond une période de 1ms ?

2 – Comment obtient-on la valeur efficace d'une tension sinusoïdale en partant de la valeur maximum (ou de crête) ?

3 – En divisant en douze parties égales, la période d'une sinusoïde et en numérotant les points obtenus de 0 à 12, à quels numéros correspond la valeur moitié de la valeur maximum de la sinusoïde ?

4 – Si l'on applique un signal sur la base d'un transistor, à quoi équivaut l'excursion du courant de base ?

5 – A quoi correspond la composante continue de la tension de collecteur ?

6 – Par quoi est donnée et à quoi correspond la composante alternative du courant de collecteur ?

7 – Comment est défini le gain en courant d'un étage amplificateur ?

8 – Le gain en puissance dépend-il des valeurs des gains en courant et en tension ?

9 – A quoi, sont dûes les distorsions du courant de collecteur ?

Fin de la leçon 15

---

LECON 16

1 – LES TROIS TYPES DE MONTAGES

Lorsque nous avons étudié les courbes caractéristiques des transistors, nous avons vu qu'il y avait deux possibilité différentes pour monter le transistor dans un circuit : montage en Base Commune et en Emetteur Commun.

Etant donné que le transistor présente trois connexions, il est naturel de penser qu'il existe une troisième façon de le monter dans le circuit qui, par analogie avec les deux autres, s'appellera montage en Collecteur Commun.

Nous n'avons pas parlé de ce type de montage dans la leçon théorique 8 et dans les leçons suivantes car, en général on ne donne pas dans les catalogues de transistors les familles de courbes caractéristiques et encore moins les paramètres relatifs à un tel montage. Ceci pour deux raisons : parce que le montage en collecteur commun peut être parfaitement étudié en utilisant les caractéristiques et les paramètres relatifs au montage en émetteur commun, et qu'ensuite un tel montage est très peu utilisé par rapport à ce dernier.

1 – 1 AMPLIFICATEUR EN BASE COMMUNE

Le schéma d'un étage amplificateur avec montage en base commune est indiqué à la figure 1. Comme on peut le voir, le collecteur est alimenté, à travers la résistance de charge R_C par une pile qui délivre une tension négative par rapport à la masse (on considère ici, un transistor du type P-N-P) tandis que l'émetteur doit être polarisé, par l'intermédiaire de la résistance R_E, par une autre pile qui délivre une tension positive par rapport à la masse.

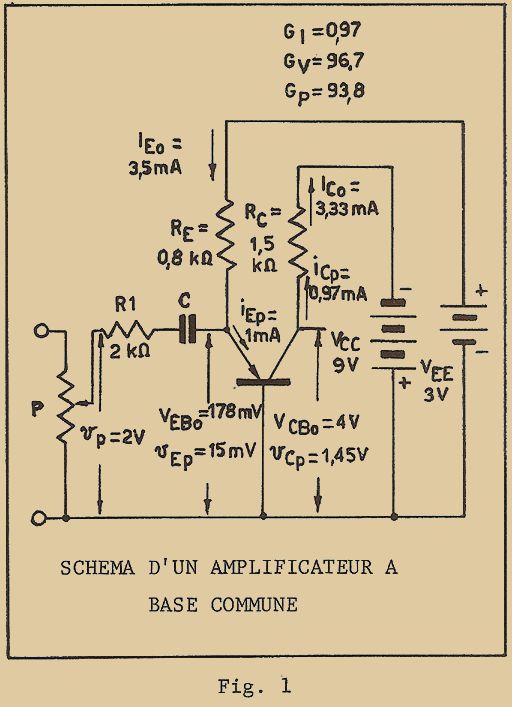
Le signal de commande est appliqué à l'émetteur par l'intermédiaire de la résistance R₁ et du condensateur C qui bloque le courant continu de polarisation ; son amplitude peut être réglée avec le potentiomètre P. Le signal de sortie est prélevé comme d'habitude sur le collecteur.

Pour pouvoir faire une comparaison entre cet amplificateur et celui étudié dans la précédente leçon, il faut faire travailler le transistor avec le même courant et la même tension de collecteur, c'est-à-dire qu'il faut encore considérer le même point de fonctionnement sur les caractéristiques du collecteur.

Pour cette raison, on choisira les mêmes valeurs de tension d'alimentation de collecteur et de résistance de charge que dans le cas du montage en émetteur commun, c'est-à-dire V_CC = 9 V et R_C = 1,5kΩ.

Si l'on considère les caractéristiques de collecteur (quadrant I figure 2), on peut tracer la droite de charge et fixer le point A' correspondant à la tension de repos V_CBo = 4 V et au courant I_Co = 3,33mA.

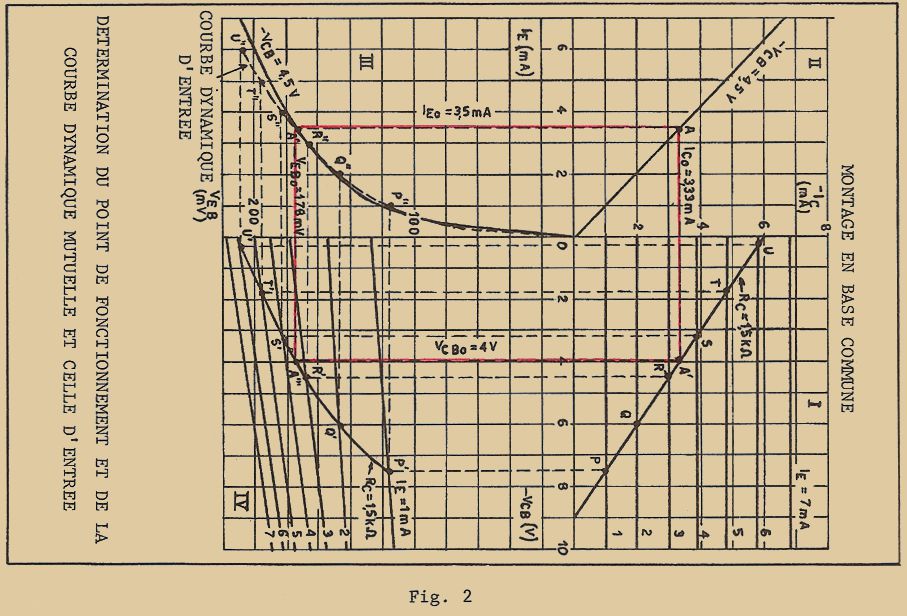
En transposant le point de repos A' sur la caractéristique mutuelle du quadrant II (qui en réalité est une caractéristique statique relative à la tension de collecteur de 4,5 V, mais qui en pratique coïncide avec la caractéristique mutuelle dynamique relative à une valeur quelconque de la résistance de charge, et en particulier à la résistance considérée 1,5kΩ puisque les caractéristiques de collecteur sont pratiquement des droites horizontales), on trouve le point A qui indique le courant nécessaire pour la polarisation de l'émetteur : I_Eo = 3,5mA.

La valeur de la résistance R_E devra être telle, qu'elle laisse circuler ce courant dans l'émetteur. En supposant que la pile de polarisation de l'émetteur a une tension VEE de 3 V seulement, la tension V_EBo qui va se stabiliser entre l'émetteur et la base est beaucoup plus faible que 3V. Ainsi pour calculer la valeur de R_E, il faut d'abord déterminer la valeur de V_EBo.

On a donc besoin de la courbe dynamique d'entrée, Il faut encore noter que la courbe d'entrée du quadrant III relative à une tension de collecteur de 4,5 V, ne peut plus être considérée comme coïncidant avec la courbe dynamique, à moins d'admettre une approximation dans le calcul, car les courbes mutuelles de tension du quadrant IV ne peuvent être considérées comme étant parfaitement horizontales (figure 2).

La construction de la courbe dynamique d'entrée est obtenue alors en se servant des courbes des quadrants I et IV et le procédé est indiqué sur la figure 2.

Il suffit de considérer les points P, Q, R, S, T, U, intersections de la droite de charge avec les différentes courbes du collecteur et de les reporter sur les courbes correspondantes du quadrant IV. En joignant les points P', Q', …etc, ainsi trouvés, on obtient une courbe, qui représente dans le quadrant IV, la droite de charge du premier quadrant. Sur cette dernière courbe, on peut marquer le point de repos A'''.

En transposant enfin, les points P', Q' etc … du quatrième quadrant au troisième, on détermine les points P'', Q'' …etc. En joignant P'', Q'' … on détermine la courbe dynamique d'entrée dessinée en pointillés sur la figure 2. Comme on peut le voir elle est sensiblement différente de la courbe statique relative à une tension de collecteur de 4,5 V.

On peut déterminer ainsi, le point de repos A''. Rappelons que le point A'' peut aussi être déterminé en menant une horizontale par le point A''', puisqu'un point de fonctionnement quelconque se trouve aux quatre sommets d'un rectangle.

En face du point A'', sur l'axe vertical dirigé vers le bas, on lit la valeur de la tension de repos de l'émetteur :

V_EBo = 178mV = 0,178 V

On peut aussi déterminer la valeur de la résistance R_E par la formule :

R_E = (V_EE - V_EBo)/I_Eo  = (3-0,178)/3,5 = (2,822 V)/(3,5mA) = 0,8kΩ environ

Supposons que l'on applique toujours, un signal de commande à l'émetteur à la fréquence de 50 Hz, aux bornes du potentiomètre P de la figure 1.

Si l'on admet que la résistance de P est très faible devant la valeur de R₁ = 2kΩ et que C est suffisamment élevé, le courant de commande de l'émetteur sera déterminé seulement par la valeur de R₁ car comme nous allons le voir sous peu, la résistance d'entrée du transistor est très faible.

En réglant P, de façon à avoir en amont de R₁ une tension v_p de 2 V crête, la composante alternative du courant d'émetteur aura une valeur crête :

i_Ep = v_p/R₁ = (2V)/(2kΩ) = 1mA

En redessinant pour plus de clarté, les caractéristiques des quadrants I, II, et III, sur la figure 3, on peut tracer de façon habituelle la sinusoïde qui représente le signal de commande en prenant comme axe de référence, la verticale qui passe par le point de repos A.

On voit ainsi que le courant de l'émetteur prend les valeurs : I_Emax = 4,5mA et I_Emin = 2,5mA et accomplit une excursion de 2mA. Les formes de courant et de la tension de collecteur se déterminent facilement par la méthode bien connue maintenant. Comme la caractéristique dynamique mutuelle de courant du deuxième quadrant est pratiquement une droite, la forme du courant de collecteur sera encore une sinusoïde ainsi que la tension de collecteur.

A partir de la construction de la figure 3, on trouve que le courant de collecteur atteint une valeur maximum I_Cmax de 4,30mA et une valeur minimum I_Cmin de 2,36mA en accomplissant une excursion de 1,94mA. Par analogie, la tension de collecteur prend une valeur V_CBmax = 5,45 V et V_CBmin = 2,55V, c'est-à-dire que son excursion est de 2,9V.

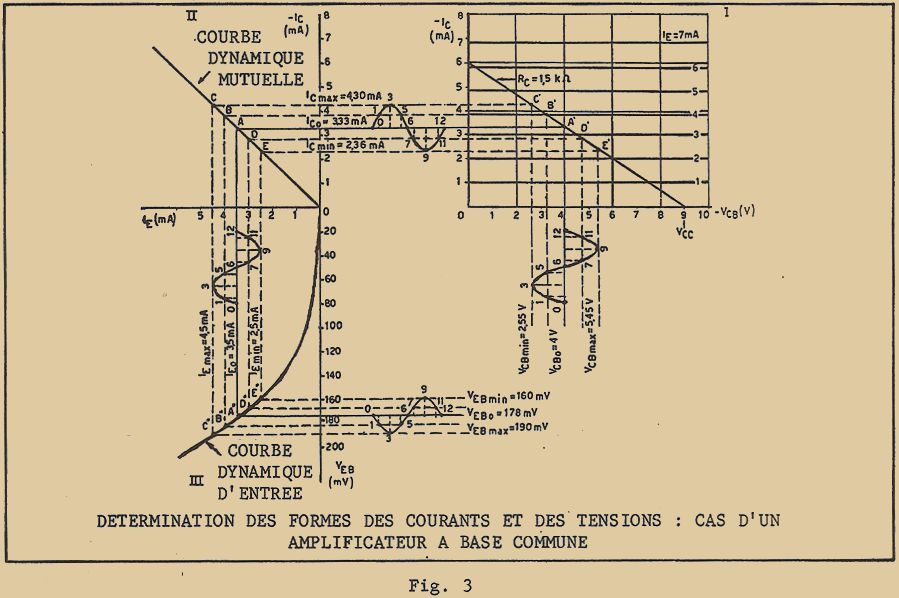
Par contre la forme de la tension de l'émetteur n'est pas parfaitement sinusoïdale, car la caractéristique dynamique d'entrée est légèrement incurvée. Ainsi, de la valeur de repos V_EBo = 178mV, la tension de l'émetteur passe à V_EBmax = 190mV et à V_EBmin = 160mV en accomplissant une excursion de 30mV. On remarquera que les deux alternances ne sont pas parfaitement égales, l'une ayant pour amplitude 18mV et l'autre 12mV.

Nous avons maintenant tous les éléments pour calculer les gains.

G_i = (I_Cmax- I_Cmin)/(I_Emax- I_Emin ) = (4,30-2,36)/(4,5-2,5) = 1,94/2 = 0,97

On trouve d'autre part, en exprimant les tensions de collecteur et d'émetteur en mV :

G_v = (V_CBmax - V_CBmin)/(V_EBmax - V_EBmin ) = (5.450-2.550)/(190-160) = 2.900/30 = 96,7

d'où le gain en puissance :

G_p = G_i x G_v = 0,97 x 96,7 = 93,8

Comme on peut le voir d'après les résultats ci-dessus, et d'après ce que l'on sait déjà, on n'a pas de gain de courant avec ce type d'amplificateur, mais l'on a un bon gain en tension. On peut donc considérer que le gain de puissance est à peu près égal au gain en tension, il est donc inférieur au gain en puissance d'un étage en émetteur commun.

Il reste encore à calculer la résistance d'entrée et de sortie d'un transistor seul et de l'étage. Pour le transistor seul, on trouve une résistance d'entrée égale à :

r_VE = (V_EBmax - V_EBmin)/(I_Emax - I_Emin) = (190-160)/(4,5-2,5) = 30/2 = 15Ω

La résistance r_VE est exprimée en ohm, car la tension et le courant de l'émetteur sont exprimés respectivement en mV et en mA, et sa valeur particulièrement faible est caractéristique de ce type de montage.

La résistance d'entrée de l'étage est obtenue facilement en mettant en parallèle r_VE et R_E et l'on trouve :

r_e = (r_E x R_E)/(r_E + R_E ) = (15 x 800)/(15+800) = 14,7Ω

En ce qui concerne la résistance de sortie du transistor, il est plus facile de la calculer à l'aide de la formule qu'avec les caractéristiques de la figure 3. Celle-ci, ainsi que celle de l'étage, sera déterminée plus tard.

Examinons maintenant les phases, en regardant la figure 3.

Quand le courant de l'émetteur augmente, le courant de collecteur augmente aussi, mais tandis que le premier croît vers des valeurs positives, le second croît vers des valeurs négatives. Ceci est dû au fait, que l'émetteur est alimenté avec une tension positive tandis que le collecteur est alimenté par une tension négative. Il en résulte que les courants d'entrée et de sortie sont en opposition de phase.

Si l'on observe maintenant les tensions, on remarque qu'à une augmentation de la tension de l'émetteur correspond une diminution de la tension du collecteur. Comme les deux tensions ont des polarités opposées, et pour la même raison que ci-dessus, elles ne se trouvent plus en opposition de phase, mais bien en phase.

La tension et le courant d'entrée se trouvent donc en phase tandis que le courant et la tension de sortie sont en opposition de phase exactement de la même façon que dans le cas de l'amplificateur en émetteur commun.

1 – 2 AMPLIFICATEUR A COLLECTEUR COMMUN

Le schéma de l'amplificateur à collecteur commun diffère de celui à émetteur commun, uniquement par la disposition de la résistance de charge.

Tandis que dans l'amplificateur à émetteur commun, la résistance de charge est placée dans le collecteur et que l'émetteur est relié à la masse, dans le montage en collecteur commun la résistance de charge est placée dans l'émetteur et le collecteur est relié directement au moins (si le transistor est du type P-N-P, ou bien au positif s'il est du type N-P-N) de la pile.

Dans ce cas, lorsque le collecteur est maintenu à un potentiel constant par rapport à la masse, il ne peut y avoir de composante alternative sur le collecteur. Pour cette raison, le schéma est dit collecteur à la masse ou collecteur commun.

Le schéma de l'amplificateur est indiqué sur la figure 4 : la résistance de charge maintenant indiqué R_E, puisqu'elle est placée dans la liaison de l'émetteur, a été choisie encore égale à 1,5kΩ, c'est-à-dire égale à celle du cas précédent pour pouvoir faire une comparaison valable avec celui-ci.

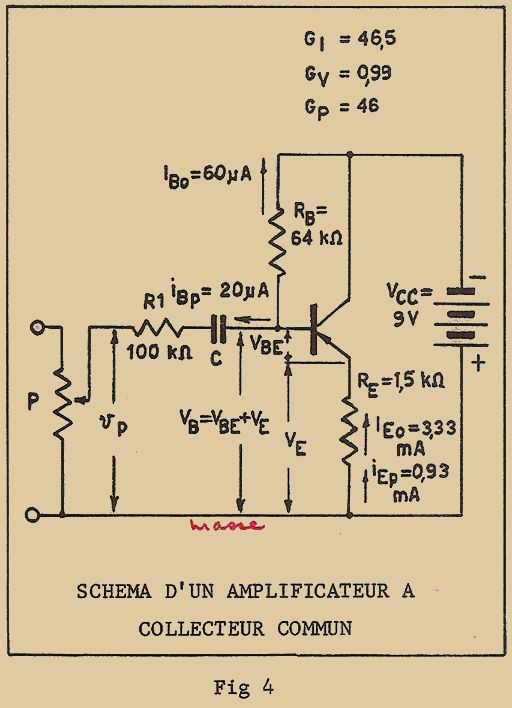
L'alimentation est encore réalisée à l'aide d'une pile unique de 9 V, et sert aussi à la polarisation de la base par l'intermédiaire de la résistance R_B, dont la valeur sera déterminée par la suite, de façon à faire travailler encore le transistor au même point de repos.

Le signal de commande est appliqué à la base par l'intermédiaire de la résistance R₁ de 100kΩ et du condensateur C de valeur appropriée, et son amplitude est encore réglée au moyen du potentiomètre P de résistance très faible pour pouvoir être négligée devant les 100kΩ de R₁.

Il faut encore remarquer que maintenant, la charge R_E est traversée par le courant de l'émetteur et non plus par celui de collecteur comme dans le cas précédent. Comme nous l'avons déjà vu, le courant IE de l'émetteur est donné par la somme du courant I_C de collecteur et du courant I_B de la base, ce dernier étant β fois plus petit que celui du collecteur : on peut donc négliger I_B devant I_C et admettre que les courants d'émetteur et de collecteur sont égaux.

Cette simplification que nous avons déjà faite en d'autres occasions (par exemple dans l'étude des circuits de polarisation) permet une étude plus rapide sur les caractéristiques du transistor. En effet, comme je vous l'ai déjà dit, on ne donne en général pas les caractéristiques relatives au montage en collecteur commun ; on doit donc se servir de celles relatives au montage en émetteur commun. Sur ces caractéristiques figure le courant de collecteur I_C et non pas IE : on voit donc l'avantage de pouvoir considérer l'égalité de I_C avec IE, car on peut ainsi utiliser les caractéristiques telles qu'elles sont.

L'approximation ainsi faite n'est valable que pour des transistors dont le β est supérieur ou égal à 25 – 30, parce que sinon, le courant de base ne serait plus suffisamment petit pour pouvoir être négligé devant celui du collecteur. Dans le cas de l'exemple ci-dessus le β est de l'ordre de 50, ce qui signifie que I_B est le cinquantième de I_C, l'erreur commise en le négligeant n'est que de 2%.

En ce qui concerne les constructions graphiques sur les caractéristiques des quadrants I et II on procède de la même manière que pour le montage émetteur commun : on trace donc la droite de charge et la courbe dynamique mutuelle de courants (figure 5).

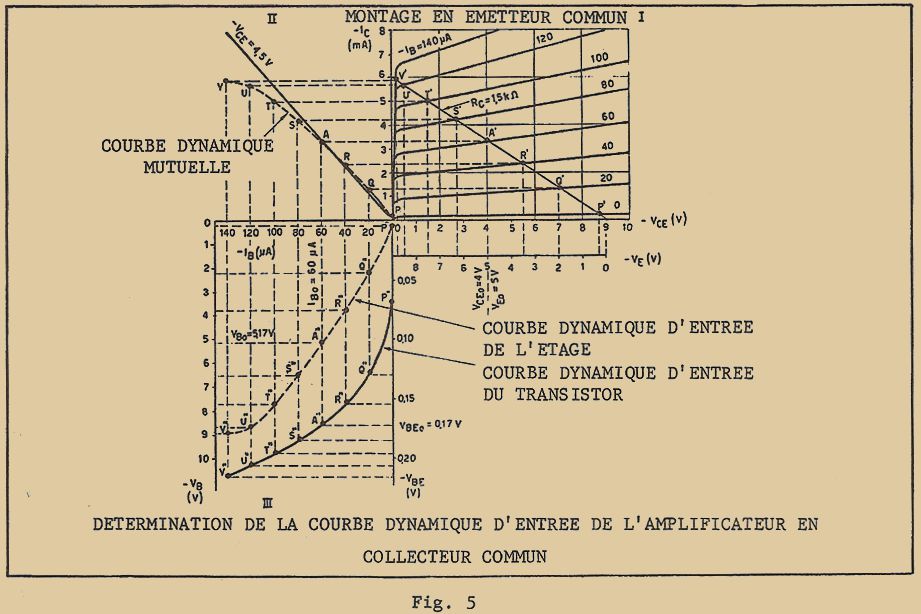
On détermine ensuite le point de repos (A' dans le premier quadrant et A dans le second) correspondant à la tension de collecteur V_CEo = 4 V : on obtient ainsi la valeur I_Co = 3,33mA et I_Bo = 60µA comme dans le cas de l'amplificateur à émetteur commun.

En ce qui concerne au contraire la courbe dynamique d'entrée, il faut faire en outre les observations suivantes. En regardant le schéma de la figure 4, on voit que le signal d'entrée, c'est-à-dire le signal de commande, est appliqué encore entre la base et la masse, comme dans le cas de l'amplificateur à émetteur commun, cependant maintenant l'émetteur est relié à la masse, non plus directement mais par l'intermédiaire de la résistance de charge R_E.

La tension d'entrée est donc appliquée, non plus simplement entre la base et l'émetteur, mais à l'ensemble jonction base-émetteur et résistance de charge qui se trouve en série. Si l'on veut tracer la caractéristique d'entrée de l'étage, il faut considérer que la tension V_B qui existe entre la base et la masse, est égale à la somme de la tension V_BE et de la tension V_E qui se stabilisent respectivement entre la base et l'émetteur et entre l'émetteur et la masse.

La courbe dynamique d'entrée donnée est relative uniquement à la seule tension V_BE et n'est valable uniquement que pour un transistor seul et non pas pour tout l'étage. La courbe dynamique d'entrée de l'étage devra donc être tracée comme défini ci-dessous et illustré figure 5.

Pour cela, il faut considérer les différents point de la droite de charge, par exemple les points d'intersection de la droite avec les différentes courbes de collecteur, correspondant aux courants de base 0, 20µA, 40µA, 60µA, etc… Pour chacun de ces points, on détermine les tensions V_E et V_BE et leur somme V_B.

En reportant dans le troisième quadrant, les valeurs de V_B ainsi trouvées en face des valeurs correspondantes de I_B, on obtient les points P''', Q''', R''', etc… qui joints par une ligne, donnent la courbe dynamique illustrée.

Pour illustrer la méthode, nous allons prendre un seul point, par exemple le point de repos : pour les autres, il suffira de faire la même construction graphique.

Le point de repos A' correspond à un courant de base I_Bo de 60µA : en abaissant la verticale passant par A' on trouve à l'intersection avec l'axe horizontal, la valeur de la tension qui se stabilise entre le collecteur et l'émetteur. Pour le point A', on trouve V_CE = 4 V. Comme entre le collecteur et la masse est appliquée la tension d'alimentation V_CC de 9 V, on en déduit que la tension aux bornes de R_E est donnée par la différence entre les 9 V appliquées et les 4 V qui se stabilisent entre collecteur et la masse.

On a donc :

V_E = V_CC – V_CE = 9 – 4 = 5 V

En répétant cette opération pour les différents points considérés, il est pratique de tracer une seconde échelle horizontale, graduée encore en volts, dont le zéro se trouve en face de la valeur V_CC = 9 V (lue sur la précédente échelle) et dont les graduations croissent de la droite vers la gauche (figure 5). Sur cette échelle, on pourra lire directement les valeurs de la tension V_E ; en effet, en prolongeant l'axe vertical passant par le point A' jusqu'à rencontrer cette nouvelle échelle, on lit directement la valeur V_Eo = 5 V.

La valeur de la tension existant entre la base et l'émetteur pour un courant de base de 60µA peut être déterminée immédiatement ; il suffit de transposer le point de repos A' du premier quadrant dans le troisième sur la courbe dynamique d'entrée du transistor, c'est-à-dire en A''. En correspondance de ce point, on lit sur l'échelle verticale V_BEo = 0,17 V.

En ajoutant les deux valeurs ainsi trouvées, on détermine la tension qui existe entre la base et la masse :

V_B = V_BE + V_E = 0,17 + 5 = 5,17 V.

Cette valeur de la tension de base et la valeur du courant de base (60µA pour le point A') doivent être reportées dans le troisième quadrant et lues respectivement sur l'échelle verticale de gauche, orientée vers le bas et indiquée sur la figure par –V_B et sur l'échelle horizontale de gauche ; on détermine ainsi le point A''', qui est un des points de la courbe dynamique d'entrée de l'étage.

Il faut remarquer, que les valeurs de la tension V_B sont nettement plus élevées que celles de la tension V_BE et on ne peut plus utiliser pour la courbe dynamique d'entrée de l'étage, la même échelle verticale que celle qui était valable pour la courbe dynamique d'entrée du transistor seul, parce que cette dernière n'était graduée qu'en dixièmes de volt. Il est donc nécessaire de tracer une seconde échelle verticale graduée jusqu'à 10 volts environ (voir figure 5) : échelle verticale de gauche orientée vers le bas.

En procédant de la même façon pour les autres points, on détermine la courbe complète. En considérant les points P', Q', R', etc… On trouve les valeurs qui sont reportées dans le tableau ci-dessous.

POINTS	IB	VE	VBE	VB
P'	0µA	0,3V	0,065V	0,365V
P'	20µA	2,0V	0,130V	2,130V
P'	40µA	3,6V	0,155V	3,755V
P'	60µA	5,0V	0,170V	5,170V
P'	80µA	6,4V	0,185V	6,585V
P'	100µA	7,5V	0,195V	7,695V
P'	120µA	8,5V	0,205V	8,705V
P'	140µA	8,7V	0,215V	8,915V

Les valeurs de la seconde et de la dernière colonne servent à déterminer les points P''', Q''', R''', etc… qui joints par une ligne, donnent la courbe dynamique dessinée (courbe en pointillés dans le troisième quadrant de la figure 5).

Après avoir déterminé ainsi la courbe dynamique d'entrée de l'étage, on peut procéder à la détermination de R_B nécessaire pour que le point de repos soit en A' comme il a été supposé avant de passer à la détermination des formes des tensions et des courants.

Par commodité, et pour plus de clarté, les courbes statiques du premier quadrant et les courbes dynamiques du deuxième et du troisième quadrant ne sont pas tracées sur la figure 6. Le calcul de R_B peut être fait de deux façons différentes. On peut utiliser la formule :

R_B = (V_CC - V_Bo)/I_Bo  = (9-5,17)/60 = 3,83/(60 ) = 0,064MΩ = 64kΩ environ

Ou bien on peut encore tracer la droite qui passe par le point de repos A'' et le point K qui indique sur l'axe vertical, la tension d'alimentation de R_B, soit V_CC = 9 V. En prolongeant cette droite jusqu'à l'intersection avec l'axe horizontal, on lit sur celui-ci (point H) la valeur 140µA.

En divisant la tension relative au point K, par le courant relatif au point H on trouve la valeur de R_B. En effet on a :

R_B = 9 V / 140µA = 0,064MΩ = 64kΩ

valeur trouvée précédemment.

Supposons maintenant, que l'on applique à la base du transistor, un signal, dont l'amplitude peut être réglée par le potentiomètre P, de façon à obtenir une composante alternative i_B dont la valeur de crête soit de 20µA, pour être dans les mêmes conditions que dans le cas de l'amplificateur à émetteur commun, de la leçon précédente.

En faisant les mêmes constructions graphiques, il sera facile de déterminer les formes du courant et de la tension du collecteur, ou mieux de la tension de l'émetteur, ainsi que celle de la tension de base.

Sur la figure 6, on trouve que le courant du collecteur (qui pour les raisons déjà énoncées sera considéré comme égal au courant de l'émetteur) prend encore les mêmes valeurs de repos I_Eo = 3,33mA, on passe à un maximum I_Emax = 4,26mA et à un minimum de 2,40mA en accomplissant une excursion de 1,86mA.

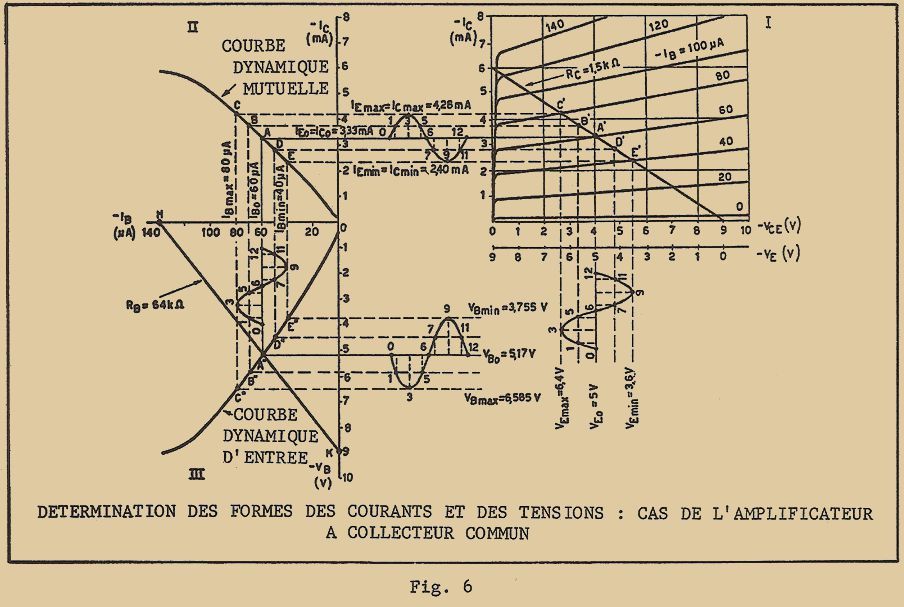
La tension entre le collecteur et l'émetteur, lue sur l'échelle indiquée – V_CE, passe de la valeur de repos de 4 V à un maximum de 5,4V et à un minimum de 2,6V ; en correspondance avec ces valeurs, la tension de l'émetteur, dont les valeurs peuvent être lues directement sur l'échelle repérée –VE, passe de la valeur de repos V_Eo = 5V à la valeur minimum VEmin = 3,6V et à la valeur maximum V_Emax = 6,4V en accomplissant une excursion de 2,8V.

Si nous passons à la tension de base nous trouvons maintenant des valeurs beaucoup plus grandes que celles relatives à l'amplificateur à émetteur commun. En effet, la tension de repos a pour valeur V_Bo = 5,17 V, et atteint la valeur maximum V_Bmax de 6,585V et minimum de 3,755 V en accomplissant une excursion de 2,83 V.

De ces valeurs, on peut déduire immédiatement les différents gains. On a en effet, en exprimant les courants d'émetteur et de base en µA :

G_i = (I_Emax - I_Emin)/(I_Bmax - I_Bmin) = (4.260-2.400)/(80-40) = 1.860/40 = 46,5

En exprimant les tensions de l'émetteur et de la base en volts on a :

G_v =  (V_Emax - V_Emin)/(V_Bmax - V_Bmin) = (6,4-3,6)/(6,585-3,755) = 2,8/2,83 = 0,99

et enfin :

G_p = G_i x G_v = 46,5 x 0,99 = 46

En comparant ces résultats avec ceux obtenus avec l'amplificateur à émetteur commun, on voit que le gain en courant est resté le même, que le gain en tension est maintenant inférieur à l'unité, ce qui signifie que la tension de sortie est plus faible que celle de l'entrée. Le gain en puissance est pratiquement le même que celui en courant.

Ainsi, la propriété particulière de l'amplificateur en collecteur commun est d'avoir un gain notable en courant (presque égal à la valeur du coefficient β du transistor), mais pas de gain en tension.

Une autre particularité de ce circuit est donnée par sa résistance d'entrée qui est notablement plus élevée que celle avec les autres montages. En effet, si l'on applique la formule en exprimant la tension en volt et le courant de base en µA (la résistance est alors donnée enMΩ) la résistance d'entrée du transistor est :

r_B = (V_Bmax - V_Bmin)/(I_Bmax - I_Bmin) = (6,585-3,755)/(80-40) = 2,83/40 = 0,071MΩ = 71kΩ

Comme la valeur de la résistance d'entrée du transistor est déterminée par les valeurs de la tension et du courant de base obtenues par l'intermédiaire de la caractéristique dynamique d'entrée, et comme cette dernière est déduite compte tenu de la droite de charge, on comprend que la valeur de r_B dépend non seulement de la caractéristique du transistor, mais aussi de la valeur de R_E.

Tandis que dans le cas de l'amplificateur en émetteur commun, la résistance d'entrée avait une valeur relativement faible (on avait trouvé r_B = 0,8kΩ) et qu'elle était pratiquement indépendante de la valeur de la résistance de charge, dans le cas de l'amplificateur en collecteur commun, elle est beaucoup plus élevée et on démontre que sa valeur est approximativement égale à β fois la valeur de la résistance de charge.

En effet, dans le cas de l'exemple, R_E = 1,5kΩ et β = 50 (comme on peut d'ailleurs le vérifier sur la figure 6, pour le point de repos A') et on a :

r_B = β x R_E = 50 x 1,5 = 75kΩ

c'est-à-dire une valeur presque égale à celle que l'on a calculée.

A cause de la présence de R_B, dont la valeur est du même ordre de grandeur que celle de la résistance d'entrée du transistor, (et non plus beaucoup plus grande que celle-ci comme c'était le cas pour les autres types d'amplificateurs), la résistance d'entrée de l'étage sera plus faible. Elle sera en effet égale, à la mise en parallèle de r_B et de R_B :

r_e = (r_B x R_B)/(r_B + R_B) = (71 x 64)/(71+64) = 33,7kΩ

En ce qui concerne la résistance de sortie nous calculerons sa valeur ultérieurement.

En examinant la figure 6, on peut dire que les courants d'entrée et de sortie sont en phase, comme pour l'amplificateur en émetteur commun. De même, les tensions à l'entrée et à la sortie (cette dernière devra être lue sur l'échelle – V_E et non pas sur – V_CE) sont en phases : ainsi à une augmentation de V_B correspond un accroissement de V_E.

2 – UTILISATION DES PARAMÈTRES

Dans l'étude faite jusqu'à maintenant sur les trois types d'amplificateurs, on a utilisé les caractéristiques de collecteur et les courbes mutuelles soit pour déterminer les gains, soit pour calculer la résistance d'entrée, soit pour voir le mécanisme de fonctionnement de l'amplificateur à transistors.

Les constructions graphiques permettent d'obtenir des résultats suffisamment précis seulement lorsque l'amplitude du signal appliqué est grande, comme nous l'avons vu dans les exemples précédents. Lorsque le signal d'entrée est très faible, comme c'est le cas dans les étages préamplificateurs où l'amplitude de crête de la tension d'entrée peut se réduire à des fractions de microampère, on peut voir rapidement en examinant les caractéristiques sur les exemples précédents, qu'il est impossible de tracer des sinusoïdes d'amplitude aussi réduite et par conséquent il est impossible de faire des constructions graphiques.

D'autre part, quand des signaux aussi faibles sont en jeu, il n'est pas en général intéressant de déterminer les formes des grandeurs de sortie, parce que dans ce cas les distorsions introduites par le transistor peuvent être négligées et l'on sait de toute façon que ces formes seront sinusoïdales.

En effet, si le signal d'entrée est très faible, la région utile de la caractéristique mutuelle (ou celle d'entrée) balayée par le point de fonctionnement sera très réduite, et même si la caractéristique dans son ensemble est courbe, la faible région balayée pourra être considérée comme étant rectiligne.

Dans ce cas, il faut déterminer les gains, les résistances d'entrée et de sortie, à l'aide de formules en utilisant les paramètres des transistors.

Naturellement, les caractéristiques gardent encore tout leur intérêt dans la détermination du point de fonctionnement et du circuit de polarisation du transistor.

Les formules relatives aux trois types d'amplificateurs seront données plus tard. Entre toutes celles qui existent, nous ne prendrons que celles qui utilisent les paramètres hybrides, étudiés en leur temps, et ferons des exemples numériques sur les circuits déjà examinés afin d'illustrer les constructions graphiques sur les caractéristiques.

2 – 1 AMPLIFICATEUR EN EMETTEUR COMMUN

Si nous voulons avoir recours à des formules utilisant des paramètres hybrides, il faut avant tout déterminer les valeurs de ces paramètres pour le point de repos choisi. Pour simplifier le problème reprenons le schéma considéré dans la leçon précédente er redessiné à la figure 7. Nous pouvons déterminer les valeurs des paramètres hybrides du transistor en utilisant le procédé illustré dans la douzième leçon théorique.

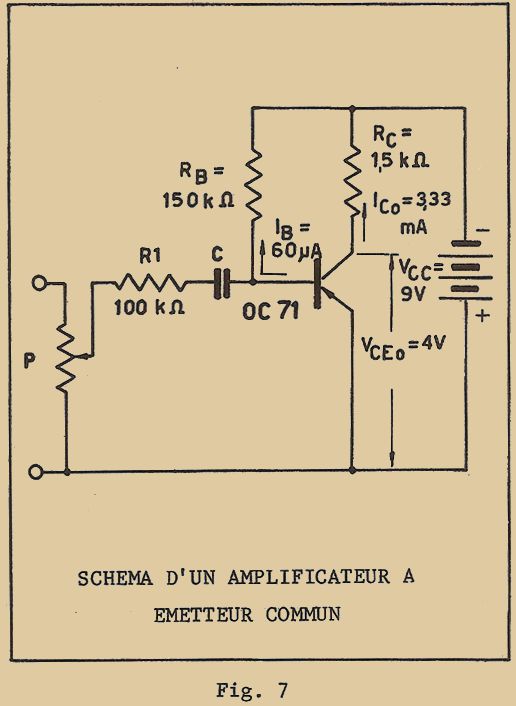
Pour le point de repos du schéma de la figure 7, caractérisé par V_CEo = 4 V et I_Co = 3,33mA, on trouve que les paramètres hybrides relatifs à ce point (nous avons omis volontairement le calcul, qui est le même que celui indiqué dans la douzième leçon) sont les suivantes :

h_11e = 0,77kΩ
h_12e = 0,00043
h_21e = β = 49,5
h_22e = 0,068mA/V

Gain en courant

En supposant que R_C = 1,5kΩ, le gain de courant est :

G_i = h_21e/(1+h_22e x R_C)) = 49,5/(1+(0,068 x 1,5)) = 49,5/(1+0,102) = 49,5/1,102 = 44,9

Résistance d'entrée

La résistance d'entrée d'un transistor est donnée par la formule :

r_B = h_11e – (G_i x h_12e x R_C) = 0,77 – (44,9 x 0,00043 x 1,5) = 0,77 – 0,029 = 0,741kΩ

Remarquez toutefois, que le terme soustractif a en général un effet pratiquement négligeable à cause de la très faible valeur de h_12e. En négligeant ce terme, on peut obtenir une formule simplifiée de la résistance d'entrée du transistor.

r_B = h₁₁e = 0,8kΩ

Dans le cas de l'amplificateur à émetteur commun, on peut dire que la résistance d'entrée du transistor coïncide pratiquement avec le paramètre h_11e.

Gain en tension

Connaissant les valeurs de G_i et de r_B on peut facilement calculer le gain en tension :

G_v = G_i R_C/r_B  = 44,9 x 1,5/0,741 = 44,9 x 2,024 = 90,87

On voit ainsi, que le gain en tension est pratiquement égal au gain en courant multiplié par le rapport de la résistance de charge divisée par la résistance d'entrée du transistor. Comme dans le cas du montage à émetteur commun la résistance de charge peut être beaucoup plus grande que la résistance d'entrée, le gain en tension sera plus grand que le gain en courant.

Gain en puissance

Le gain en puissance est toujours donné par le produit du gain en courant par celui de la tension : G_p = G_i x G_v ; mais en tenant compte de la formule précédente donnant le gain en tension, le gain en puissance peut être trouvé directement à partir du gain en courant par la formule suivante :

G_p = G_i2 x R_C/r_B  = (44,9)2 x 1,5/0,741 = 2.016 x 2,024 = 4.080

Résistance de sortie

Il reste encore à calculer la résistance de sortie du transistor. Les formules utilisées en général, donnent la conductance de sortie g_c qui pour le montage en émetteur commun est pratiquement égale au paramètre h_22e. On a donc :

G_c = h_22e = 0,068mA/V

r_C = 1/g_c  = 1/h_22e  = 1/0,068 = 14,7kΩ

Les résistances d'entrée et de sortie de l'étage seront données en mettant respectivement en parallèle r_B et R_B, et r_c avec R_C. Nous trouvons :

r_e = (r_B x R_B)/(r_B + R_B ) = (0,741 x 150)/(0,741+150 ) = 0,737kΩ

r_S = (r_C x R_C)/(r_C + R_C ) = (14,7 x 1,5)/(14,7+1,5 ) = 1,36kΩ

En comparant ces résultats, avec ceux obtenus dans la précédente leçon, nous voyons qu'ils sont parfaitement comparables. Les différences que l'on peut remarquer sont imputables en majeure partie au fait que dans les calculs sur les caractéristiques, on prend les valeurs de crête à crête, c'est-à-dire les excursions des différentes grandeurs, sans tenir compte qu'elles ne sont pas parfaitement sinusoïdales, mais plus ou moins distordues.

En conclusion, on peut dire que les valeurs obtenues sur les caractéristiques sont relatives au fonctionnement du transistor pour des signaux de grandes amplitude, tandis que elles obtenues à l'aide des formules sont valable à un fonctionnement pour des signaux de faible amplitude.

Ainsi, on dit souvent, que la méthode graphique (c'est-à-dire les constructions graphiques sur les caractéristiques) est adaptée dans le cas du fonctionnement avec des signaux forts, tandis que la méthode analytique (c'est-à-dire le calcul à l'aide des formules) est adaptée au cas du fonctionnement avec des signaux faibles.

Nous continuerons dans la prochaine leçon, l'étude de l'amplification et verrons en particulier le cas de l'amplificateur à base commune et en collecteur commun.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 15^ème LEÇON THÉORIQUE

1 – Une période de 1 ms correspond à une fréquence de 1kHz.

2 – La valeur efficace d'une tension sinusoïdale est égale à la valeur de crête multipliée par 0,707.

3 – La sinusoïde prend des valeurs égales à la moitié de la valeur maximum aux points 1, 5, 7 et 11.

4 – L'excursion du courant de base, équivaut à la valeur de crête à crête du signal appliqué.

5 – La composante continue de la tension du collecteur est la tension de repos du collecteur.

6 – La composante alternative du courant du collecteur est donnée par les variations du courant de collecteur et provoquée par le signal d'entrée et constitue le signal de sortie.

7 – Le gain en courant d'un étage amplificateur est défini comme le rapport entre la composante alternative du courant de collecteur et la composante alternative du courant de base.

8 – Le gain en puissance dépend des gains en courant et en tension parce qu'il est donné par leur produit.

9 – Les distorsions du courant de collecteur sont dûes à la non linéarité de la caractéristique mutuelle en courant.

---

EXERCICES DE RÉVISION SUR LA 16^ème LEÇON THÉORIQUE

1 – Quels sont les trois types d'amplificateurs à transistors ?

2 – Quelle est la différence de schéma entre l'amplificateur à collecteur commun et celui en émetteur commun ?

3 – Quand peut-on utiliser les constructions graphiques sur les caractéristiques ?

4 – Quand faut-il avoir recours aux formules pour le calcul des gains et des résistances d'entrée et de sortie ?

5 – Quelle est la valeur approximative de la résistance d'entrée d'un amplificateur à émetteur commun ?

6 – Quel est le gain en tension de l'amplificateur en collecteur commun ?

7 – Quel est approximativement le gain en courant de l'amplificateur en collecteur à la masse ?

8 – La résistance d'entrée d'un amplificateur collecteur à la masse est-elle plus grande ou plus faible que celle d'un amplificateur avec l'émetteur à la masse ?

9 – Connaissant le gain en courant G_i et le gain en puissance G_p, peut-on déterminer directement le gain en tension G_v ?

Fin de la leçon 16

---

LECON 17

1 – UTILISATION DES PARAMÈTRES

(suite de l'étude de la 16ème leçon Théorique)

1 – 1 AMPLIFICATEUR A BASE COMMUNE

On utilise encore des formules analogues à celles vues dans la 16ème leçon dans le cas du montage en émetteur commun. La seule différence est que les paramètres hybrides à utiliser sont ceux relatifs au montage en base commune.

Si l'on reprend le schéma de la figure 1 (16ème théorique) dans lequel le point de repos est encore caractérisé par une tension et par un courant de collecteur dont les valeurs sont respectivement 4 V et 3,333mA, et si l'on utilise les paramètres hb donnés dans la douzième leçon théorique, on trouve :

h_11b = 15Ω = 0,015kΩ
h_12b = 0,0006
h_21b = α = 0,98
h_22b = 0,00135mA/V

En appliquant les formules, on trouve les résultats ci-après :

Gain en courant

G_i = h_21b/(1+h_22b x R_c ) = 0,98/(1+ 0,00135 x 1,5) = 0,98/1,002 = 0,978

Remarquez que cette valeur est très proche du coefficient d'amplification α

Résistance d'entrée du transistor (avec R_c = 1.500Ω)

r_VE = h_11b + (G_i x h_12b x R_c) = 15 + (0,978 x 0,0006 x 1500) = 15 + 0,88 = 15,88Ω

On peut remarquer, que comme les valeurs de r_VE et h_11b sont faibles, il est préférable de les exprimer en Ω, plutôt qu'en kΩ comme dans l'exemple du montage en émetteur commun.

Gain en tension

G_v = G_i R_c/r_E  = 0,978 1.500/15,88 = 0,978 x 94,45 = 92,37

Gain en puissance

G_p = G_i2 R_c/r_E  = (0,978)2 x 1.500/15,88 = 0,956 x 94,45 = 90,29

Résistance de sortie du transistor

La formule donne la conductance de sortie g_c.

Dans le cas du montage en base commune, on ne peut pas admettre que g_c soit simplement égal au paramètre h_22b, et il faut encore tenir compte d'autres paramètres ; d'où la formule suivante :

g_c = h_22b + (h_21b x h_12b)/(h_11b+R_G )

où R_G est donné par la mise en parallèle de toutes les résistances qui sont branchées entre l'émetteur et la masse ou entre l'émetteur et la pile de polarisation. Dans le cas de la figure 1 (théorique 16), il faut calculer la mise en parallèle de R_E et R₁ (en effet R₁ est branché à la masse par l'intermédiaire de P, mais on suppose que la valeur de P peut être négligée devant R₁) ; ainsi, comme R_E = 0,8kΩ et R₁ = 2kΩ, on a :

R_G = (R_E x R₁)/(R_E+R₁ ) = (0,8 x 2)/(0,8+2) = 0,57kΩ

En introduisant cette valeur dans la formule précédente, et en se rappelant que h_22b est exprimé en mA/V, tandis que h_11b et R_G le sont en kΩ, on obtient :

g_c = 0,00135 + (0,98 x 0,0006)/(0,015+0,57) = 0,00135 + 0,000588/0,585 = 0,00135 + 0,001 = 0,00235mA/V

d'où r_c = 1/g_c  = 1/0,00235 = 425kΩ

Enfin les résistances d'entrée et de sortie de l'étage s'obtiendront en mettant en parallèle r_VE et R_E d'une part, et r_c et R_C d'autre part. On peut remarquer tout de suite que comme R_E est beaucoup plus grand que r_VE (800Ω contre 15,88Ω) et que r_c est beaucoup plus grand que R_c (425kΩ contre 1,5kΩ), ce qui est typique pour le montage en base commune, la résistance d'entrée r_e est pratiquement égale à la résistance d'entrée du transistor r_VE et que la résistance de sortie r_S est pratiquement égale à la résistance de charge R_C.

En effet, si l'on effectue les calculs, on trouve :

r_e = 15,58Ω, ce qui est pratiquement égal à 15,88Ω et r_S = 1.498Ω ce qui est pratiquent égal à 1.500Ω.

1 – 2 AMPLIFICATEUR A COLLECTEUR COMMUN

On peut utiliser pour l'amplificateur à collecteur commun, les mêmes formules que celles utilisées dans le montage en base commune en remplaçant les paramètres hb par les paramètres hc, c'est-à-dire ceux relatifs au montage en collecteur commun. Comme ces paramètres ne sont pas en général donnés dans les manuels, on préfère avoir recours à d'autres formules qui utilisent elles les paramètres he, c'est-à-dire ceux relatifs au montage en émetteur commun.

En regardant le schéma de la figure 4 (Théorique 16), on voit que le point de repos du transistor est encore le même que celui de la figure 7 de la même théorique (V_CEo = 4 V, I_Co = 3,33mA). Les paramètres he seront donc les mêmes que ceux qui ont été considérés pour le montage en émetteur commun. On trouve :

Gain en courant

G_i = (1+ h_21e)/(1+(h_22e x R_E)) = (1+49,5)/(1+(0,068 x 1,5)) = 50,5/1,102 = 45,8

Résistance d'entrée du transistor

r_B = h_11e + (G_i x R_E) = 0,77 + (45,8 x 1,5) = 0,77 + 68,7 = 69,47Ω

Gain en tension

G_v = G_i x R_E/( r_B ) = 45,8 x 1,5/69,47 = 45,8 x 0,0216 = 0,989

A cause de la valeur élevée de la résistance d'entrée par rapport à la résistance de charge, le gain en tension résultant est légèrement plus petit que 1, et indépendant de la valeur de R_c ; ceci est une des particularités du montage en collecteur commun, comme on l'a déjà vu précédemment.

Gain en puissance

G_p = G_i2 R_E/r_B  = (45,8)2 x 1,5/69,47 = 2.097,6 x 0,0216 = 45,3

Le gain de puissance est donc légèrement inférieur au gain en courant.

Résistance de sortie du transistor

On doit calculer tout d'abord la conductance de sortie g_E. La valeur R_G qui apparait dans la formule suivante est donnée par la mise en parallèle de R_B et R₁ (figure 4 – théorique 16) ; étant donné que R_B = 64kΩ et que R₁ = 100kΩ, R_G sera égal à 39kΩ.

On obtient donc :

g_E = h_22e + (1+ h_21e)/(h_11e+ R_G ) = 0,068 + (1+49,5)/(0,77+39) = 0,068 + 50,5/39,77 = 0,068 + 1,27 = 1,338mA/V

et

r_VE = 1/g_E  = 1/1,338 = 0,747kΩ

Enfin les résistances d'entrée et de sortie de l'étage se calculant comme à l'habitude, on trouve :

r_e = (r_B x R_B)/(r_B+R_B ) = (69,47 x 64)/(69,47+64) = 33,3kΩ

r_s =  (r_E x R_E)/(r_E+R_E ) = (0,747 x 1,5)/(0,747+1,5) = 0,50kΩ

En comparant ces résultats avec ceux trouvés par la méthode graphique, on peut voir qu'il n'y a pas une trop grande différence.

2 – COMPARAISON ENTRE LES DIFFÉRENTS TYPES D'AMPLIFICATEUR -

Après tous ces calculs, qui peuvent présenter un aspect confus et incompréhensible, il est bon de les rassembler dans un tableau unique pour pouvoir les comparer plus facilement et étendre les conclusions aux trois types d'amplificateurs.

Dans le tableau de la figure 1, ont étés rassemblés les résultats obtenus pour les trois types d'amplificateurs dans le cas d'un fonctionnement avec signaux faibles. En observant les valeurs des gains, on peut noter que, pour l'amplificateur à émetteur commun, le gain en courant et le gain en tension sont tous les deux élevés, et qu'ainsi le gain en puissance est très élevé.

Pour l'amplificateur en base commune, le gain en courant est de l'ordre de 1, ce qui signifie que ce type d'amplificateur ne présente pas d'amplification en courant. Le gain en tension est par contre comparable à celui de l'amplificateur en émetteur commun. Le gain en puissance lui, est pratiquement égal à celui en tension et est donc nettement inférieur à celui du montage en émetteur commun.

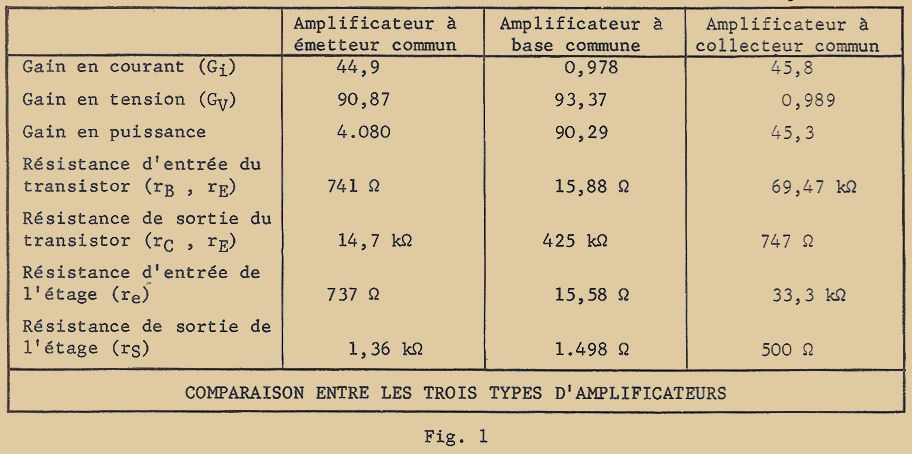
Pour l'amplificateur en collecteur commun, les résultats sont différents. On note encore un gain en courant comparable à celui du montage en émetteur commun, tandis que le gain en tension est presque égal à 1. Le gain en puissance est donc pratiquement égal au gain en courant.

En d'autres termes on peut dire, que tandis que l'amplificateur en émetteur commun amplifie aussi bien le courant que la tension, l'amplificateur en base commune amplifie seulement la tension et que l'amplificateur en collecteur commun amplifie seulement le courant.

En passant aux résistances d'entrée et de sortie du transistor, on note que dans le cas du montage en base commune, on a une résistance d'entrée très faible et une résistance de sortie très élevée ; dans le cas du montage en collecteur commun, c'est le contraire : une résistance d'entrée très élevée et une faible résistance de sortie. L'amplificateur en émetteur commun présente au contraire des résistances de valeur intermédiaire entre les précédentes et assez proches entre elles, bien que la résistance d'entrée soit en général inférieure à celle de sortie.

On peut donc faire les conclusions suivantes :

• L'amplificateur en base commune est surtout adapté dans le cas où l'on ne désire qu'un gain en tension ou dans le cas, où le transistor ne doit servir que comme liaison entre un circuit à faible résistance et un à résistance élevée.
• L'amplificateur en collecteur commun sert dans les cas, où l'on ne désire obtenir qu'un gain en courant, ou bien lorsque l'on désire passer d'un circuit à forte résistance à un circuit à faible résistance.
• L'amplificateur en émetteur commun enfin est indiqué lorsque l'on désire obtenir un fort gain en tension ainsi qu'un grand gain en courant, c'est-à-dire lorsque l'on désire avoir un gain en puissance élevé. En ce qui concerne les résistances, il convient pour passer d'un circuit à résistance moyennement faible à un circuit à résistance moyennement élevée.

Dans les le tableau de la figure 2, ont été rassemblées les propriétés générales en ce qui concerne les gains, les résistances d'entrée et de sortie et le déphasage entre les signaux d'entrée et de sortie pour les trois types d'amplificateurs.

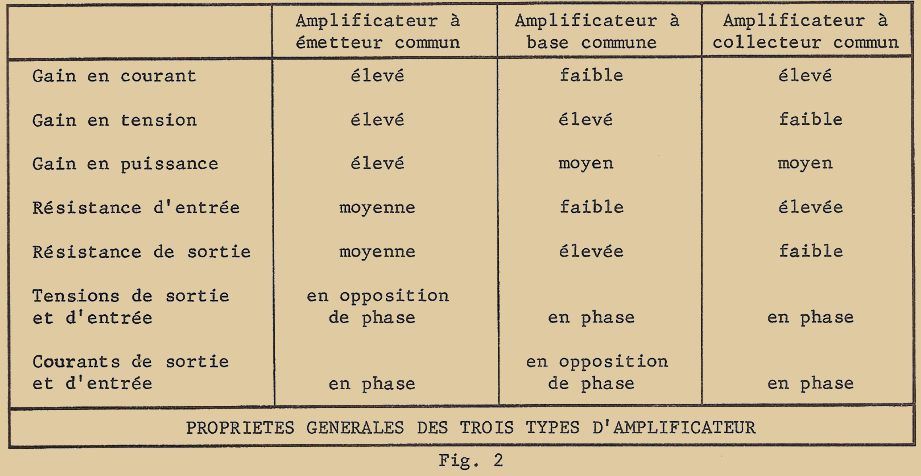
3 – AMPLIFICATEUR AVEC STABILISATION THERMIQUE

Dans les deux précédentes leçons on a étudié les trois types d'amplificateurs à transistors du point de vue de leur comportement et de leurs propriétés en présence d'un signal, en négligeant pour simplifier le problème de la stabilisation thermique, que nous avons d'ailleurs étudié dans la onzième leçon de théorie.

Pour obtenir un amplificateur stabilisé du point de vue thermique il suffit de se rappeler les circuits de polarisation décrits dans la leçon correspondante, en leur apportant une légère modification, comme nous le verrons sous peu.

Il faut remarquer avant tout, qu'en pratique il n'y a vraiment que l'amplificateur à émetteur commun qui doive être stabilisé : en effet, l'amplificateur en base commune est déjà stable du point de vue thermique, de par sa nature même, et l'amplificateur à collecteur commun a un coefficient de stabilité S en général faible, à cause de la résistance R_E d'émetteur de valeur toujours relativement élevée.

Il suffira de considérer uniquement l'amplificateur à émetteur commun.

3 - 1 AMPLIFICATEUR A EMETTEUR COMMUN

La stabilisation de l'amplificateur à émetteur commun est obtenue par l'intermédiaire des circuits de polarisation, illustrés dans la onzième leçon et que je vous ai reportés à la figure 3.

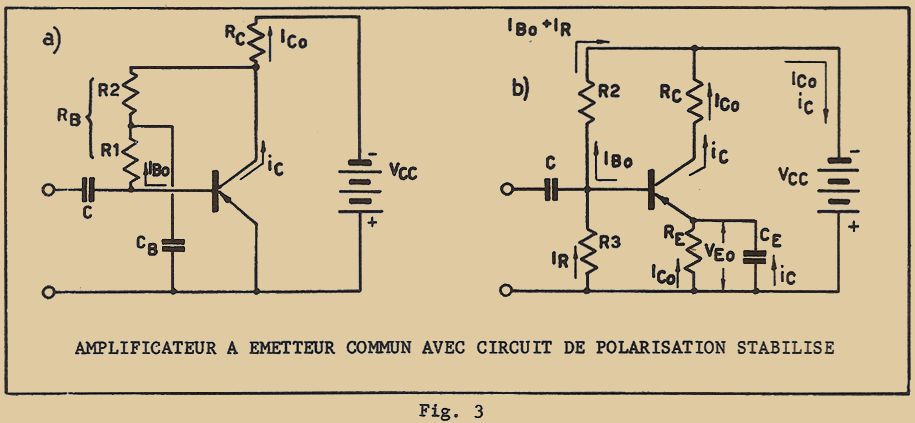
Étant donné que de tels circuits fonctionnent sur le principe de la contre-réaction de collecteur ou d'émetteur, il est évident qu'ils vont tendre à stabiliser aussi les accroissements et les diminutions du courant de collecteur quand ces variations sont provoquées par le signal d'entrée même.

En d'autres termes, ceci signifie que la contre-réaction qui se manifeste aussi pour le courant continu de polarisation (composante continue) se manifeste aussi pour le signal lui-même (composante alternative), avec comme effet, la réduction de l'amplification de l'étage, puisque le circuit réduit aussi les variations du courant (et donc de la tension) du collecteur qui constituent le signal de sortie.

Cet effet de contre-réaction est d'autant plus élevé que le circuit de polarisation présente un degré de stabilité thermique plus grand ; ainsi dans le cas où la stabilité est très grande, le gain de l'étage peut être tellement réduit que ce dernier devient pratiquement inutilisable.

Afin d'éviter de tels inconvénients, les circuits de polarisation sont modifiés par l'adjonction d'un condensateur. Dans le cas d'un circuit de contre-réaction de collecteur (figure 3a), la résistance de base est partagée en deux résistances R₁ et R₂ et le condensateur est intercalé entre leur point de jonction et la masse.

De cette façon les variations rapides de la tension du collecteur (qui constituent le signal de sortie) ne peuvent être transmises sur la base et provoquer l'effet de contre-réaction. En effet, si la capacité du condensateur C_B est suffisamment élevée, la tension aux bornes de C_B, ne peut suivre les variations de la tension du collecteur et reste pratiquement constante : le courant de polarisation de base I_Bo reste ainsi lui aussi pratiquement constant.

Pour des variations lentes de la tension du collecteur, (dûes par exemple à la variation de la température), le condensateur n'a plus la capacité suffisante pour maintenir constante la tension à ses bornes et éliminer l'effet de contre-réaction ; sa présence ne perturbe donc pas l'action stabilisatrice du circuit.

En ce qui concerne le comportement du circuit en présence d'un signal appliqué sur la base, il faut remarquer encore que la résistance de charge (comme on pourrait le démontrer facilement) est maintenant constitué par la mise en parallèle de R_C et de R₂, c'est-à-dire que maintenant la valeur résultante est un peu plus faible.

Dans la plupart des cas, la valeur de R₂ est notablement plus élevée que R_C et on peut en général négliger son effet, et considérer comme résistance de charge la seule valeur de R_C.

Si nous passons maintenant au circuit stabilisé par contre-réaction d'émetteur (figure 3b), l'effet de contre-réaction peut être évité pour le signal, c'est-à-dire pour la composante alternative, en maintenant constante la tension aux bornes de R_E, c'est-à-dire en plaçant un condensateur C_E en parallèle sur cette dernière.

En effet de cette façon, en considérant que la valeur de la capacité C_E est suffisamment élevée, presque toute la composante alternative i_C passe à travers C_E seulement, car le passage offert est plus facile qu'au travers de R_E. On peut donc dire que C_E court-circuite la résistance d'émetteur pour le courant alternatif : ainsi, pour i_C, tout se passe comme si l'émetteur était relié directement à la masse et qu'il n'y avait aucun effet de contre-réaction.

La composante continue I_Co par contre, ne peut pas passer par le condensateur d'émetteur, et elle est obligée de traverser la résistance R_E : pour elle, l'effet de contre-réaction indispensable pour la stabilisation thermique, se manifeste donc.

Les deux composantes I_C et I_Co se superposent à l'intérieur du transistor et parcourent ensemble la résistance R_C : en conclusion le courant I_Co traverse R_E et R_C, tandis que i_C ne traverse seulement que R_C. Ceci, va provoquer un comportement différent du circuit suivant les deux composantes du courant de collecteur, et nous devrons considérer deux droites de charge différentes sur les courbes caractéristiques du transistor.

La droite qui est seulement valable pour la composante continue et qui servira à déterminer le point de repos (c'est-à-dire lorsque I_Co intervient seul) sera appelé Droite de charge statique et correspondra à la valeur R_C + R_E puisque I_Co parcourt ces deux résistances ensemble.

L'autre droite, uniquement valable pour la composante alternative sera appelé droite de charge dynamique et correspondra à la seule valeur de la résistance R_C. Elle sera utilisée pour toutes les constructions graphiques relatives à la détermination des signaux de sortie, des gains et des résistances d'entée et de sortie.

C'est uniquement la valeur seule de R_C qu'il faudra considérer dans les calculs d'amplification à l'aide des formules que nous avons vues précédemment.

Par analogie avec la dénomination des droites de charge, on dira R_C + R_E, est la résistance de charge statique et que R_C est la résistance de charge dynamique.

Le circuit amplificateur avec stabilisation thermique présente l'avantage d'être moins sensible aux effets de la température, et ne présente d'autre part, aucun inconvénient majeur par rapport au circuit non stabilisé.

Pour mieux mettre en évidence les différences qui peuvent exister entre les deux circuits, il est bon de faire un exemple numérique.

Considérons pour cela, le schéma reporté sur la figure 4 ; il est dérivé du schéma considéré dans la leçon théorique 15 ; la stabilisation thermique est obtenue à l'aide de la résistance d'émetteur R_E = 0,6kΩ et la base est polarisée par R₂ – R₃ dont les valeurs sont calculées (comme nous allons le voir sous peu) de façon à obtenir le même point de repos que dans l'exemple précédent.

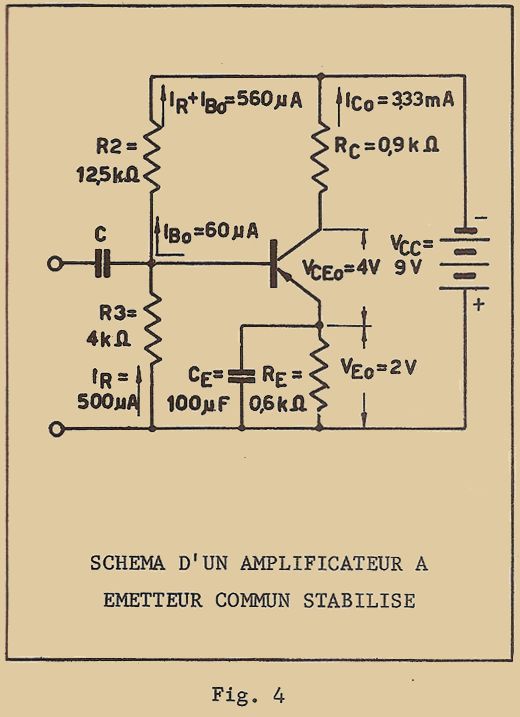
Pour déterminer le point de repos, il faut tout d'abord tracer sur la caractéristique de la figure 5, la droite de charge statique correspondant à la valeur de la résistance statique R_C + R_E = 0,9 + 0,6 = 1,5kΩ. Cette valeur est la même que celle du circuit non stabilisé de la 15ème leçon ; la tension d'alimentation ayant la même valeur V_CC = 9 V, la droite de charge statique sur les courbes caractéristiques du collecteur sera encore la même.

En fixant encore le point de repos A' correspondant à V_CEo = 4 V et I_Co = 3,33mA, le courant de polarisation de la base devra être encore de 60µA. Pour obtenir cette valeur du courant de polarisation de la base, on trouve facilement en négligeant la tension V_BE qui existe entre base et émetteur et en admettant un courant IR de 500µA dans le pont :

V_Eo = I_CO x R_E = 3,33mA x 0,6kΩ = 2 V environ

R₂ = (V_CC - V_Eo)/(I_R + I_Bo ) = (9-2)/(0,5+0,06) = (7 V)/(0,56mA) = 12,5kΩ

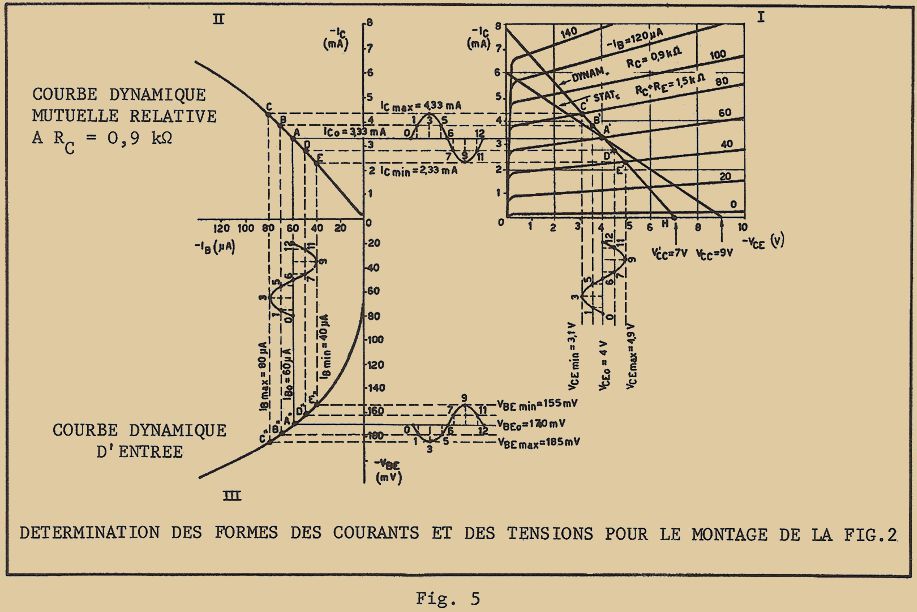
R₃ = V_Eo/I_R  = (2 V)/(0,5mA) = 4kΩ

Avec ces valeurs, on peut vérifier facilement que le coefficient de stabilisation S est de l'ordre de 3, c'est-à-dire que la stabilité thermique obtenue est très élevée.

Pour déterminer les formes des tensions et des courants, il est nécessaire de tracer la droite de charge dynamique correspondant à la résistance dynamique R_C = 0,9kΩ. Celle-ci passe nécessairement par le point de repos A' parce que lorsque l'on applique le signal sur la base, le point de fonctionnement se déplace le long de la droite de charge dynamique de part et d'autre de A'.

Un autre point de la droite de charge dynamique peut être facilement déterminé sur l'axe horizontal de la tension, en face de la valeur de la tension V'_CC = V_CEo + (I_Co x R_C) = 4 + (3,33 x 0,9) = 4 + 3 = 7 V (point H sur la figure 5). Il suffit alors de joindre A' à H.

Nous pourrons maintenant maintenant tracer la courbe dynamique mutuelle, qui doit correspondre à la droite de charge dynamique, parce que c'est cette dernière qui compte pour la composante alternative du courant de collecteur et pour la détermination des formes du signal de sortie.

En réalisant les constructions bien connues maintenant, on trouve la courbe indiquée dans la figure 5 du deuxième quadrant.

Nous pourrons alors procéder à la détermination des formes et des amplitudes des excursions des différents courants et tensions.

En supposant que l'on fasse circuler dans la liaison de la base, le seul courant de commande dont l'amplitude est de 20µA, et en procédant comme d'habitude en ce qui concerne les constructions graphiques on trouve les résultats de la figure 5.

En examinant cette figure, on pourra faire la remarque suivante qu'il n'y a rien de changé par rapport au circuit non stabilisé de la 15ème leçon, en ce qui concerne la tension V_BE ; par contre, en ce qui concerne les excursions du courant et de la tension du collecteur, les effets sont maintenant différents à cause de l'inclinaison différente de la droite de charge.

Pour cette raison, les gains en courant et en tension, et donc en puissance, seront différents, comme on peut le vérifier par le calcul.

Gain en courant – (en exprimant I_C et I_B en µA)

G_i = (I_Cmax-I_Cmin)/(I_Bmax- I_Bmin ) = (4.330-2.330)/(80-40) = 2.000/40 = 50

Gain en tension – (V_CE et V_BE exprimés en mV)

G_v = (V_CEmax-V_CEmin)/(V_BEmax-V_BEmin ) = (4.900-3.100)/(185-155) = 1.800/30 = 60

Gain en puissance

G_p = G_i x G_v = 50 x 60 = 3.000

Par rapport au montage non stabilisé, vous remarquerez un accroissement léger du gain en courant (50 au lieu de 46,5) et une diminution notable du gain en tension (60 au lieu de 93,33) ; en conséquence le gain en puissannce est notablement diminué (3.000 au lieu de 4.340).

Ces diminutions sont pratiquement dûes à la valeur de la résistance dynamique de charge bien plus faible maintenant (0,9kΩ au lieu de 1,5kΩ). Le choix de cette valeur plus faible de R_C a été rendu nécessaire pour obtenir le même point de repos que pour le circuit non stabilisé.

La résistance d'entrée du transistor est encore la même que dans le cas du montage non stabilisé, parce que l'excursion de la tension V_BE est restée inchangée. On a donc : (en exprimant V_BE en mV et I_B en µA).

r_B = (V_BEmax-V_BEmin)/(I_Bmax-I_Bmin ) = (185-155)/(80-40) = 30/40 = 0,75kΩ

Par contre, la résistance d'entrée de l'étage r_e est plus faible maintenant, non seulement parce que la résistance branchée entre la base et le négatif de la pile est de valeur plus faible (R₂ = 12,5kΩ – figure 4, au lieu de R_B = 150kΩ sur la figure 2 de la 15ème leçon théorique), mais aussi à cause de la présence de R₃ dont la valeur est faible et qui se trouve branchée entre la base et la masse, c'est-à-dire directement en parallèle sur l'entrée de l'étage.

On peut encore dire que la résistance d'entrée de l'étage résulte de la mise en parallèle de la résistance d'entrée du transistor et de la résistance R_B, comme dans le cas du circuit non stabilisé, si l'on considère que R_B est donné à son tour, par la mise en parallèle de R₂ et R₃ (comme ceci a été déjà fait lors de l'étude des circuits de stabilisation dans la 11ème leçon théorique).

Dans le cas de notre exemple, nous avons :

R_B = (R₂ x R₃)/(R₂+R₃ ) = (12,5 x 4)/(12,5+4) = 50/16,5 = 3,03kΩ

D'où :

r_e = (r_B x R_B)/(r_B+R_B ) = (0,75 x 3,03)/(0,75+3,03) = 0,6kΩ = 600Ω environ

On peut donc conclure en disant que l'avantage de la stabilisation thermique se paie par deux inconvénients distincts : moins de gain en tension et en puissance et résistance d'entrée de l'étage plus faible.

4 – LIAISONS ENTRE DEUX ÉTAGES

Les amplificateurs que nous avons étudiés jusqu'à maintenant, étaient composés d'un seul étage, c'est-à-dire par un seul transistor. Très souvent par contre, le gain d'un seul étage n'est pas suffisant et on a alors le problème de liaison entre deux ou plusieurs étages, de façon à obtenir un amplificateur à plusieurs étages.

Faire la liaison entre deux étages signifie qu'il faut prélever le signal à la sortie d'un étage et l'appliquer à l'entrée de l'étage suivant, c'est-à-dire qu'il faut relier la sortie du premier étage (par exemple le collecteur) à l'entrée du second étage (par exemple à la base).

Si pour simplifier le problème, on considère deux étages identiques on peut tout de suite remarquer qu'en général la composante continue de la tension de sortie et celle de la tension d'entrée ne sont pas égales entr'elles et qu'on ne peut donc relier directement la sortie d'un étage à l'entrée de l'étage suivant sans risquer de perturber complètement les polarisations.

Le couplage entre deux étages devra donc être fait non pas par une simple liaison, mais à l'aide d'un élément qui a la propriété de ne laisser passer que la composante alternative, qui constitue le signal même, et au contraire de bloquer la composante continue que représentent les tensions et les courants de polarisation.

Deux types d'éléments différents présentent cette propriété ; le condensateur et le transformateur. Avec le premier, on obtient le couplage capacitif, avec le second, le couplage inductif.

Du point de vue électrique, le second type de liaison présente des avantages par rapport au premier, mais un transformateur quel qu'il soit coûtera toujours plus qu'un simple condensateur.

Pour cette raison, on utilise dans la mesure où c'est possible, la liaison par capacité qui est toujours plus économique.

Pour pouvoir étudier les propriété des deux types de liaisons, nous examinerons deux exemples dans le cas courant d'un amplificateur à émetteur commun.

4 – 1 LIAISON PAR CAPACITÉ

Considérons un amplificateur à deux étages égaux entr'eux, et pour simplifier chacun identique au schéma déjà vu à la figure 4.

Le couplage capacitif entre deux étages sera réalisé simplement en reliant le collecteur du premier transistor à la base du second transistor par l'intermédiaire d'un condensateur de capacité convenable, comme nous le verrons ultérieurement. Le schéma complet de l'amplificateur à deux étages est reporté à la figure 6.

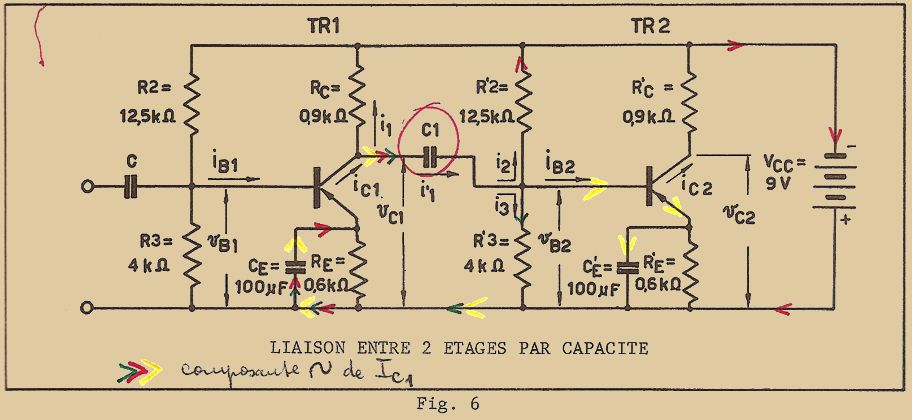
En ce qui concerne le second étage, il est parfaitement identique à celui de la figure 4, et il n'y a rien à ajouter de nouveau.

Si l'on suppose que sa base est commandée avec un signal sinusoïdal, dont l'amplitude est de 20µA crête, on pourra utiliser les constructions graphiques de la figure 5.

En ce qui concerne le premier étage, il faut encore faire les remarques suivantes :

La composante continue du courant collecteur parcourt comme pour l'autre étage, la résistance de collecteur R_C et celle de l'émetteur R_E ; la résistance de charge statique est donc encore égale à R_C + R_E.

La composante alternative du courant de collecteur i_C se partage en deux parties, comme il apparait clairement sur la figure 6 : le courant i₁ (il traverse la résistance R_C, la pile d'alimentation et retourne au transistor au travers du condensateur C_E) et le courant i'₁ (ce dernier se dirige au contraire vers le second transistor). A son tour ce courant i'₁ se subdivise en trois parties, i₂, i3 et i_B2 qui tous trois retournent au transistor TR₁ de la façon suivante : C₁, R'₂, la pile et C_E (pour i₂) ; C₁, R'₃, C_E (pour i3) ; C₁, jonction base-émetteur (c'est-à-dire r'_B : résistance d'entrée de TR₂), C'_E, C_E (pour i_B2).

Comme d'autre part, la pile présente une résistance très faible au passage du courant alternatif comme vous le savez déjà, ainsi que les condensateurs C₁, C_E et C'_E, ces éléments pourront être négligés en ce qui concerne la composante alternative des courants. On peut donc dire que le courant i_C1 se partage en quatre courants qui traversent respectivement les quatre résistances R_C, R'₂, R'₃ et r'_B. Ces résistances devront être considérées comme étant en parallèle pour la composante alternative du courant de collecteur de TR₁ et leur valeur équivalente R_D constitue la résistance de charge dynamique de TR₁.

Nous avons déjà vu d'autre part, que la mise en parallèle de R'₂, R'₃ et r'_B n'est autre que la résistance d'entrée r_e du second étage, nous pourrons dire que dans le cas de liaison par condensateur, la résistance dynamique de charge d'un étage est constituée par la mise en parallèle de la résistance R_C du collecteur de l'étage considéré et de la résistance d'entrée r_e de l'étage suivant.

Dans le cas de l'exemple de la figure 6, où R_C = 0,9kΩ et r_e = 0,6kΩ (valeur calculée pour le schéma de la figure 4 et encore valable pour le second étage de la figure 6 puisque les étages son identiques), la résistance dynamique de charge du premier étage devient :

R_D = (R_C x r_e)/(R_C+r_e ) = (0,9 x 0,6)/(0,9+0,6) = 0,36kΩ = 360Ω

Sur la caractéristique de la figure 7 cette droite de charge passe encore par le point de repos A' et par le point H de l'axe horizontal, correspondant à la tension :

V'_CC = V_Eo + (I_Co x R_D) = 4 + (3,33 x 0,36) = 4 + 1,2 = 5,2 V

Pour déterminer le gain, on utilisera la construction graphique habituelle, en supposant que la base du transistor est encore parcourue par un courant alternatif de 20µA crête. Il faut encore remarquer qu'un courant de cette valeur ne peut en réalité circuler dans la base de TR₁ (figure 6) : en effet, s'il en était ainsi, le courant de commande de la base de TR₂ serait trop important et le transistor ne pourrait travailler dans des conditions correctes et le signal de sortie de TR₂ serait complètement distordu.

En procédant comme à l'habitude, on obtient les constructions indiquées à la figure 7 et les résultats suivants :

Gain en courant – (I_C et I_B en µA)

G_i = (I_Cmax- I_Cmin)/(I_Bmax- I_Bmin ) = (4.340-2.320)/(80-40) = 2.020/40 = 50,5

Gain en tension – (V_CE et V_BE exprimés en mV)

G_v = (V_CEmax- V_CEmin)/(V_BEmax- V_BEmin ) = (4.400-3.600)/(185-155) = 800/30 = 26,67

Gain en puissance

G_p = G_i x G_v = 50,5 x 26,67 = 1.347 environ

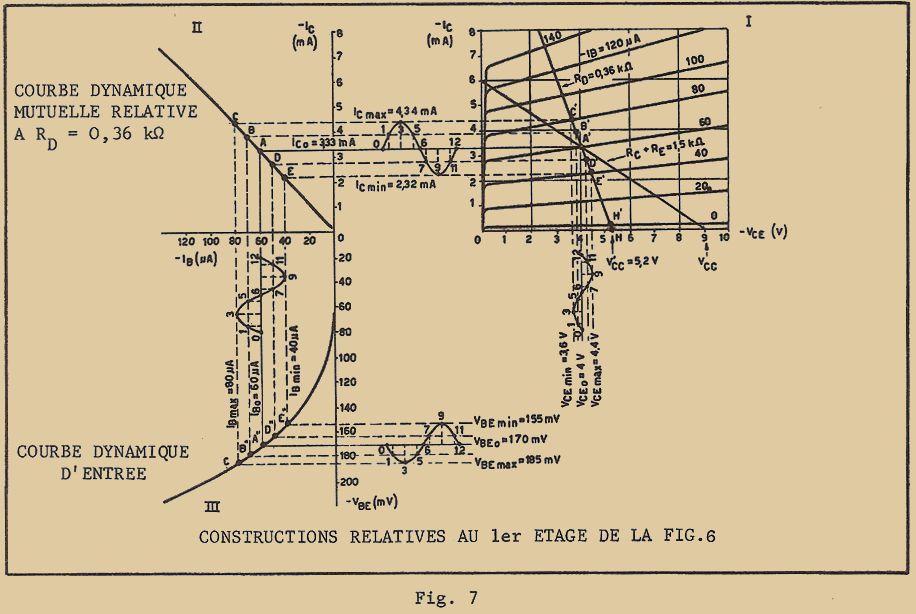
En ce qui concerne le circuit d'entrée, rien n'est changé par rapport à la figure 5, et la résistance d'entrée du transistor est encore de 0,75kΩ et celle de l'étage de 0,6kΩ.

La faible valeur de la résistance de charge, encore diminuée par rapport à celle du cas précédent, à cause de la faible valeur de r_e qui se trouve en parallèle sur R_C, provoque une diminution importante du gain en tension, et une augmentation légère du gain en courant.

Dans le cas d'un amplificateur à deux étages, le gain en courant G_i calculé n'exprime pas grand-chose. En effet, la valeur G_i indique de combien de fois la composante alternative i_C1 du courant de collecteur est plus grande que la composante alternative i_B1 du courant de commande de la base. Mais, si l'on regarde le schéma de la figure 6, on voit qu'une partie du courant i_C1 est utilisée pour commander l'étage suivant. Il est donc plus intéressant d'exprimer le gain de l'étage comme étant le rapport entre le courant de commande i_B2 du second étage (au lieu du courant i_C1 de sortie du premier étage) et du courant i_B1 de commande du premier étage.

La valeur de i_B2 peut être déterminée facilement en observant que la composante alternative v_C1 de la tension du collecteur est égale à la composante alternative v_B2 de la tension de la base de l'étage suivant.

D'après la loi d'ohm, on a : v_C1 = i_C1 x R_D et v_B2 = i_B2 x r'_B

D'où :

i_B2 = v_B2/r'_B = (i_C1 x R_D)/r'_B

En tenant compte de ce que G_i = i_C1/i_B1 , le gain effectif de l'étage (qui est toujours plus petit que le gain calculé selon les résultats obtenus à la figure 7), peut être déterminé à l'aide de la formule suivante :

G'_i = i_B2/i_B1  = (i_C1 x R_D)/(i_B1 x r'_B ) = (G_i x R_D)/r'_B

où R_D et r'_B devront être exprimées dans les mêmes unités, en kΩ ou en Ω.

Dans le cas de figure 6, où R_D = 360Ω et r'_B = 750Ω, on trouve un gain effectif de :

G'_i = (G_i x R_D)/r'_B  = (50,5 x 360)/750 = 24,24

Le gain effectif est donc plus faible (environ la moitié de celui de l'exemple) que le gain propre de l'étage calculé auparavant. On peut maintenant savoir quelle doit être la valeur de crête de i_B1 pour obtenir une valeur de crête de i_B2 de 20µA ; on a en effet :

i_B1 = i_B2/(G'_i) = 20/24,24 = 0,825µA environ

Le gain effectif de puissance G'_p, sera réduit lui aussi par rapport à G_p :

G'_p = G'_i x G_v = 24,24 x 26,67 = 646,48

En comparant cette valeur de gain de puissance effectif que l'on a obtenu pour le premier étage de la figure 6 couplé par capacité au second étage, avec celui de l'étage seul de la figure 4, on note une réduction sensible (de 3.000 à 646,48, c'est-à-dire de 5 fois).

Cette réduction est dûe à la nature même du couplage par capacité, en ce sens, qu'en reliant le collecteur de TR₁ à l'étage suivant, qui présente une faible résistance d'entrée, on a une forte diminution du gain en tension (à cause de la faible valeur de R_D qui en résulte), et aussi une notable réduction du gain en courant (à cause du partage de i_C1 en plusieurs courants).

Il faut donc remarquer que la diminution du gain est surtout dûe au fait que l'on relie un étage dont la résistance de sortie est relativement élevée, à un étage dont la résistance d'entrée est faible. Cette diminution est d'autant plus forte que la résistance d'entrée du second étage est plus faible par rapport à la résistance de sortie du premier.

On voit donc que le couplage par capacité provoque une diminution importante des gains. Si les étages sont en base commune, cette réduction de gain devient intolérable, car comme vous le savez déjà la résistance de sortie d'un tel étage est élevée, tandis que sa résistance d'entrée est très faible.

Pour cette raison, on n'utilise jamais la liaison par capacité pour des étages en base commune.

Si l'on veut connaître le gain total de cet amplificateur à deux étages, il suffira de multiplier entr'eux les gains des étages. Ainsi dans notre exemple, le gain total en courant G_it sera :

G_it = G'_i x G_i = 24,24 x 50 = 1.212

Dans la prochaine leçon, nous continuerons l'étude des amplificateurs et examinerons le cas du couplage par induction.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 16^ème LEÇON THÉORIQUE

1 – Il y a trois sortes de types d'amplificateurs à transistors : à émetteur commun ; à base commune ; à collecteur commun.

2 – La différence essentielle de schéma entre un amplificateur à collecteur commun et à émetteur commun est la suivante : dans le premier, la résistance de charge est placée dans l'émetteur, dans le second elle est placée dans le collecteur.

3 – On peut faire des constructions graphiques sur les caractéristiques lorsque l'amplificateur travaille avec des signaux forts.

4 – On utilise de préférence les formules, lorsque l'amplificateur travaille avec des signaux faibles.

5 – La résistance d'entrée d'un amplificateur à émetteur commun coïncide approximativement avec la valeur du paramètre h_11e

6 – Le gain en tension d'un amplificateur en collecteur commun est toujours inférieur à l'unité.

7 – L'amplificateur collecteur à la masse a un gain en courant presque égal à la valeur du coefficient β du transistor

8 – La résistance d'entrée d'un amplificateur en collecteur commun est beaucoup plus élevée que celle de l'amplificateur à émetteur commun.

9 – Oui. Le gain en tension G_v est G_v = G_p/G_i puisque G_p = G_i x G_v

---

EXERCICES DE RÉVISION SUR LA 17^ème LEÇON THÉORIQUE

1 – Quelle est la valeur approximative de la résistance d'entrée d'un amplificateur en collecteur commun ?

2 – Quel le type d'amplificateur qui a le plus grand gain en puissance ?

3 – Dans un amplificateur à base commune est-ce le gain en tension ou en courant qui est le plus grand ?

4 – Quel est le type d'amplificateur qui a la plus faible résistance d'entrée ?

5 – La résistance d'entrée d'un amplificateur en émetteur commun dépend-elle de la valeur de la résistance de charge ?

6 – A quoi sert le condensateur que l'on place en parallèle sur la résistance d'émetteur d'un amplificateur stabilisé ?

7 – Quelles sont les valeurs des résistances de charge dynamique et statique dans un amplificateur stabilisé ?

8 – Qu'appelle-t-on couplage capacitif ou inductif ?

9 – Par quoi est donnée la valeur de la résistance de charge dynamique dans le cas d'un couplage capacitif ?

Fin de la leçon 17

---

LECON 18

Dans la dernière leçon, nous avons étudié la stabilisation thermique dans les amplificateurs à transistors. Nous avons examiné ensuite, comment on pouvait relier deux étages à l’aide d’un couplage capacitif.

Nous étudierons dans cette leçon, un autre mode de liaison appelé Couplage inductif.

1 – COUPLAGE INDUCTIF

Les deux étages de la figure 4 de la précédente leçon peuvent être couplés par induction à l’aide d’un transformateur. Comme il s’agit d’amplificateurs basse fréquence, le transformateur sera obligatoirement du type à noyau de fer (tôles au silicium à haute perméabilité) sur lequel sont bobinés les enroulements primaire et secondaire. Les dimensions du transformateur sont proportionnelles à la puissance électrique mise en jeu dans le circuit : comme dans les étages préamplificateurs, on se trouve devant des puissances très faibles, de quelques dixièmes de watts au maximum, la section du noyau sera de l’ordre d’une fraction de cm² et la hauteur d’un peu plus de 1cm au maximum.

Le schéma des deux étages couplés par l’intermédiaire d’un transformateur se présente comme sur la fig. 1. Le second étage reste encore identique au premier.

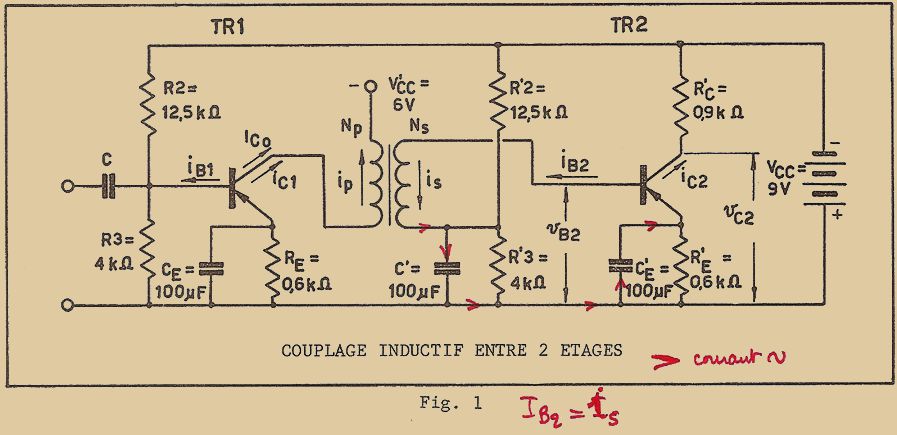
Le premier étage devra être étudié de nouveau d’abord du point de vue de son comportement avec la composante continue, ensuite au point de vue de la composante alternative. Il est bon de considérer tout d’abord le comportement du transformateur seul, que je vous ai redessiné pour plus de clarté à la figure 2.

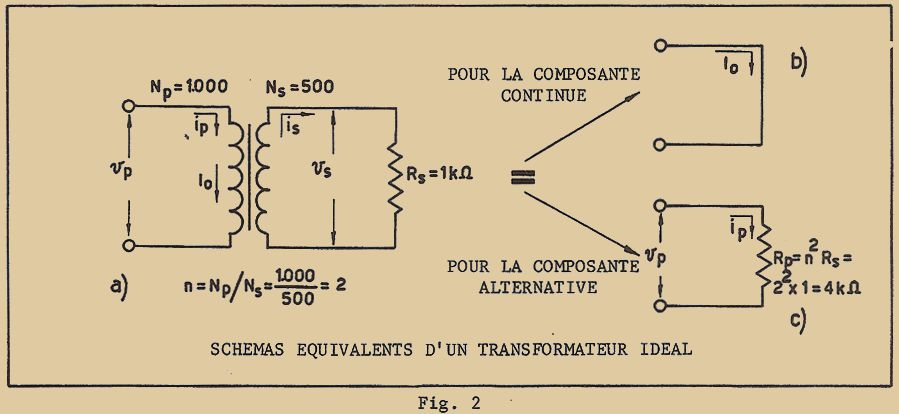
On supposera avant tout, que le transformateur est idéal, c’est-à-dire qu’il est sans pertes. Ceci signifie que l’on admet que la résistance ohmique des deux enroulements est très faible et que l’on peut la négliger (ce qui signifie que les pertes par effet Joule dans les conducteurs sont considérées comme étant nulles). On suppose d’autre part que les tôles sont composées d’un matériau excellent, et que l’on admet que les pertes par effet d’hystérésis sont nulles aussi.

Les suppositions sont faites ainsi afin d’étudier d’une façon plus simple l’étage amplificateur. On pourra ensuite tenir compte des effets de ces pertes, dans une étude plus exacte ; cette simplification ne modifie en rien le principe de fonctionnement du circuit.

Considérons donc le transformateur de la figure 2 et supposons que son primaire est constitué par 1.000 spires (N_p = 1.000) et que le secondaire comprend 500 spires (N_s = 500). On définit comme étant le rapport de transformation n, le rapport entre le nombre de spires du primaire et le nombre de spires au secondaire. On a donc :

n = N_p/N_s  = 1.000/500 = 2

Faisons maintenant traverser le primaire par un courant continu I_o de quelquesmA ; ce courant va magnétiser le noyau du transformateur et celui-ci va être parcouru par un certain flux de valeur constante (ce flux sera constant, parce que le courant I_o est constant lui-même) ; aucune tension n’est alors induite dans le secondaire et aucun courant ne traversera cet enroulement, ni la résistance de charge R_S sur lequel il est fermé.

Pour le courant continu, le transformateur se comporte donc comme un simple conducteur (constitué par l’enroulement primaire) parcouru par le courant I_o. Le schéma équivalent du transformateur se réduit donc au conducteur représenté à la figure 2-b.

Supposons maintenant que l’on superpose à la composante continue I_o une composante alternative i_p, obtenue en appliquant aux bornes du primaire, une tension alternative v_p, par exemple de 2 V (nous considérons ici pour simplifier la valeur efficace, mais il est évident que l’on peut considérer aussi la valeur de crête).

La composante alternative i_p va magnétiser à son tour le noyau du transformateur en superposant son effet à celui de la composante continue de tout à l’heure. Le flux total dans le noyau du transformateur pourra être ainsi considéré comme étant la résultante d’un flux continu, dû à I_o et d’un flux alternatif dû à i_p.

Ce dernier seul, parce qu’alternatif, va induire une tension alternative v_s dans le secondaire et fera donc circuler dans le secondaire et dans la résistance R_S, un courant alternatif i_s. Comme les tensions alternatives du primaire et du secondaire sont proportionnelles au nombre de spires des enroulements, on peut déterminer tout de suite, la valeur de v_s : on a en effet :

v_s = v_p/n = 2/2 = 1 V

Si l’on suppose que la charge est de 1 kΩ, on peut déterminer tout de suite le courant alternatif qui en résulte : i_s = v_s/R_S  = (1 V)/(1 kΩ) = 1mA. La puissance P que le transformateur délivre à la résistance de charge n’est autre que le produit de la tension du secondaire v_s par le courant du secondaire i_s : P = v_s x i_s = 1V x 1mA = 1mW

Comme on a supposé que le transformateur n’avait pas de pertes, la même puissance P devra être appliquée au primaire du transformateur. Le produit de la tension primaire v_p et du courant primaire i_p doit donc redonner la valeur P calculée ci-dessus.

Comme nous connaissons déjà la tension v_p, il est facile d’en déduire la valeur du courant i_p qui est donc :

i_p = P/v_p  = (1mW)/(2 V) = 0,5mA

Vous remarquerez dès maintenant, que tandis que la tension primaire est le double de celle du secondaire (d’une façon plus générale v_p est n fois plus grand que v_s, c’est-à-dire v_p = v_s x n), le courant primaire est cette fois la moitié du courant secondaire (d’une façon plus générale i_p est n fois plus petit que i_s c’est-à-dire i_p = i_s/n)

Supposons maintenant, que l’on enlève le transformateur et qu’on le remplace par une résistance R_p. Le circuit qui alimentait auparavant le transformateur, ne "s’en apercevra pas", si la valeur de R_p est telle que le courant absorbé garde toujours la même valeur i_p, c’est-à-dire si la puissance P reste la même que tout à l’heure.

Pour que i_p reste le même, il faut que R_p ait pour valeur :

R_p = v_p/i_p  = (2 V)/(0,5mA ) = 4 kΩ

La valeur de R_p peut être déterminée directement à partir de la valeur de R_s, en tenant compte de ce que v_p = v_s x n et que i_p = i_s / n. En effet si l’on substitue ces valeurs de v_p et i_p dans la formule précédente, on obtient :

R_p = v_p/i_p  = (v_s x n)/(i_s/n) = v_s/i_s x n²

Mais comme v_s/i_s n’est autre que R_s, on a :

R_p = R_s x n² = 1 kΩ x (2)² = 1 kΩ x 4 = 4 kΩ

et l’on trouve la même valeur que tout à l’heure.

Ainsi donc, en ce qui concerne le courant alternatif, le transformateur se comporte exactement comme une résistance R_p de valeur n² fois la valeur de la résistance R_s branchée au primaire. Le schéma équivalent du transformateur, pour le courant alternatif, est celui qui est représenté à la figure 2-c.

Vous remarquerez que la résistance équivalente ramenée au primaire du transformateur dépend et du rapport de transformation, et de la valeur de la résistance de charge branchée au secondaire. Le transformateur opère donc non seulement une transformation des valeurs de tension et de courant, mais aussi une transformation de la valeur de la résistance ; ainsi il peut transformer la valeur de la charge R_S en une autre valeur R_p quelconque, plus grande ou plus petite ; il suffira de choisir pour cela un rapport n convenable, entre le nombre des spires du primaire et le nombre de spires au secondaire, et qui sera donné par :

n = √(R_p/R_s)

où les valeurs de R_p et de R_s doivent être exprimées toutes les deux dans les mêmes unités, c’est-à-dire toutes les deux en ohms ou en kΩ.

Nous pouvons maintenant, après cette parenthèse sur le fonctionnement du transformateur, revenir au circuit de la figure 1. Pour la composante continue, le transformateur se comporte comme une simple connexion, c’est-à-dire tout se passe comme si le collecteur était relié directement à la pile : la résistance de charge statique correspond donc à la valeur de la résistance R_E d’émetteur soit 0,6kΩ.

Si l’on veut encore avoir le même point de repos que celui des exemples précédents, c’est-à-dire le point A’ de la caractéristique de collecteur correspondant à la tension V_CEo = 4 V et au courant de base I_Bo = 60µA, la droite de charge statique passera par ce point et par le point K qui se trouve sur l’axe horizontal correspondant à la valeur de la tension :

V'_CC = V_CEo + (I_Co x R_E) = 4 + (3,33 x 0,6) = 4 + 2 = 6 V (figure 3).

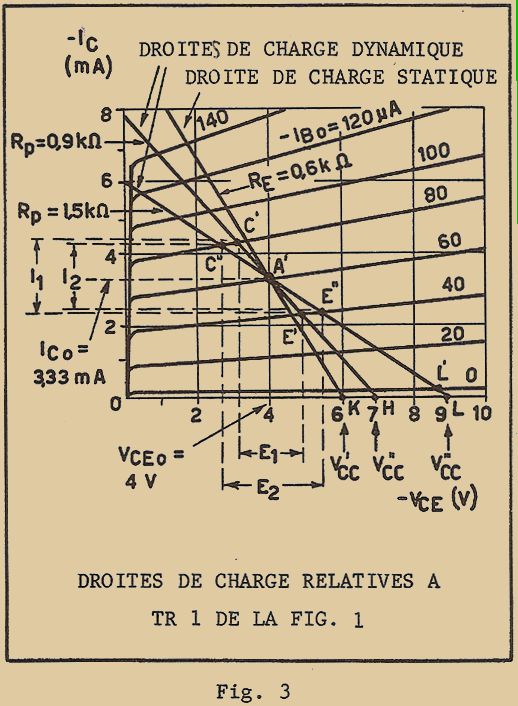
En se rappelant que la droite de charge statique rencontre l’axe horizontal exactement au point correspondant à la valeur de la tension d’alimentation du collecteur on en déduit qu’ayant remplacé la résistance de charge R_c de la figure 4 (Théorique 17) par le primaire du transformateur, on obtient le même point de repos en alimentant le collecteur avec seulement 6V au lieu de 9V.

Ce fait était presque intuitif, si l’on pense que le transformateur ne présente aucune résistance pour la composante continue, c’est-à-dire qu’il n’y a aucune chute de tension aux bornes du primaire. C'est un des premiers avantages du transformateur.

Si nous passons maintenant à la droite de charge dynamique, nous remarquerons que la résistance R_E n’intervient pas, puisqu’en parallèle sur celle-ci il y a le condensateur CE, dont la capacité est élevée : il ne reste donc plus que le transformateur qui se comporte comme une résistance R_p. La résistance de charge dynamique correspond donc à cette valeur de R_p.

Pour déterminer la valeur de R_p il suffit de connaître le rapport de transformation et la résistance R_s sur laquelle est fermé le secondaire.

On voit tout de suite que le secondaire est fermé directement sur la résistance d’entrée re du second étage et que dans ce cas, re coïncide avec la résistance d’entrée du transistor TR₂ seul.

En effet, en examinant le schéma de la figure 1, on voit que l’extrémité supérieure du secondaire est reliée directement à la base de TR₂ ; l’extrémité inférieure est reliée au contraire à l’émetteur par l’intermédiaire une liaison de très faible résistance pour le courant alternatif, et tout se passe, comme s’il y avait une liaison directe entre l’extrémité inférieure du secondaire et l’émetteur.

Aux bornes du secondaire, se trouve donc branchée la jonction base-émetteur de TR₂ : tout le courant secondaire i_s traverse donc cette jonction (c’est-à-dire i_B2 = i_s) et toute la tension du secondaire v_s est appliqué entre la base et l’émetteur. Le secondaire peut donc être considéré comme fermé sur la résistance d’entrée r_B du transistor seul.

Etant donné que pour le courant continu, le secondaire se comporte comme une simple connexion entre la base de TR₂ et le point de jonction de R'₂ et R'₃ on doit en conclure que sa présence n’influence pas du tout le fonctionnement du circuit de polarisation, ni du point de vue de la stabilisation, ni de celui du point de repos. Celui-ci reste donc le même que dans le cas de la figure 2 (Théorique 17) et r_B garde la même valeur calculée précédemment soit 0,75kΩ.

Cette valeur peut être transformée en une valeur R_p quelconque comme nous l’avons vu ci-dessus. Si nous désirons que la résistance de charge en dynamique soit encore de 0,9 kΩ, comme dans le cas de la figure 2 (Théorique 17), il suffira de choisir un transformateur, dont le rapport n soit égal à :

n = √(R_p/R_s ) = √(0,9/0,75) = √1,2 = 1,1 environ

ce qui signifie que si par exemple le secondaire comporte 100 spires, le primaire devra en avoir 100 x 1,1 = 110.

Dans ces conditions, le transistor va travailler avec une charge dynamique de 0,9kΩ et la droite de charge correspondante va passer par le point A’ et le point H (figure 3). Sur la caractéristique de collecteur, nous aurons encore la même droite de charge que celle que nous avions pour le schéma de la figure 2 de la précédente théorique. Il est évident que les résultats des constructions graphiques seront encore ceux que l’on avait à la figure 3 (revoir théorique 17).

Les gains de l’étage seront encore les mêmes que ceux que l’on avait précédemment :

G_i = 50  ;  G_v = 60  ;  G_p = 3.000

Vous voyez immédiatement que la liaison par transformateur ne provoque pas de diminution dans les gains, comme cela avait été le cas dans la liaison par capacité (figure 4 – Théorique 17).

En considérant en effet le gain effectif en courant, et en tenant compte de ce que maintenant, à cause de la présence du transformateur, i_B2 (c’est-à-dire i_s) est n fois plus grand que i_C1 (c’est-à-dire i_p), on trouve :

G'_i = i_B2/i_B1  = n x i_C1/i_B1  = n x G_i = 1,1 x 50 = 55

Si l’on veut avoir un courant de commande de TR₂ de 20µA crête il suffira de commander TR1 par un courant de base de 20/55 = 0,364µA au lieu de 0,825µA comme dans la précédente leçon.

Le gain effectif en courant a donc plus que doublé (55 au lieu de 24,24). De même le gain effectif en tension a augmenté ; en effet, et en tenant compte de ce que v_B2 (c’est-à-dire v_s) est maintenant égal à v_C1 (c’est-à-dire à v_p) divisé par n, on obtient :

G’v = v_B2/v_B1  = (v_C1/n)/v_B1  = G_v/n = 60/1,1 = 54,55 environ

c’est-à-dire que le gain en tension est plus du double de celui obtenu dans le cas d’une liaison par capacité (54,55 au lieu de 26,67).

En ce qui concerne le gain effectif en puissance, il est facile de voir qu’il n’est pas sensiblement diminué par rapport au cas de la figure 2 (théorique 17). Il suffit en effet de penser que la puissance de sortie de TR1 n’est autre que la puissance au primaire du transformateur, et que celle-ci est égale à la puissance au secondaire, c’est-à-dire à la puissance d’entrée de TR₂ ; ce qui signifie que G'_p est obligatoirement égal à G_p, c’est-à-dire égal encore à 3.000.

En comparant les gains obtenus avec un étage du type de celui de la figure 2 – Théorique 17) et ceux obtenus en reliant ce dernier à un autre étage identique soit par une liaison par capacité, (figure 4 – Théorique 17), soit par un couplage inductif (figure 1), on voit tout de suite qu’avec le second type de liaison, on évite les pertes de gain introduites par le premier type, et que l’on a de plus l’avantage de pouvoir utiliser une tension d’alimentation plus faible (6 V dans notre exemple au lieu de 9V).

2 – CHARGE OPTIMUM ET ADAPTATION D’IMPÉDANCE

En examinant la figure 3, on voit comment en augmentant le rapport de transformation (ce qui revient à augmenter R_p), la droite de charge dynamique continue à passer toujours par le point de repos A’, mais devient de plus en plus inclinée sur l’axe horizontal. Ainsi, si l’on passe du rapport n = 1,1 (pour lequel R_p = 0,9kΩ) au rapport n = 1,41 la valeur de R_p devient :

R_p = n² x R_s = (1,41)2 x 0,75 = 2 x 0,75 = 1,5kΩ

La droite de charge passe alors par le point L de l’axe horizontal correspondant à la valeur de la tension

V''_CC = V_CEo + (I_CEo x R_p) = 4 + (3,33 x 1,5) = 4 + 5 = 9V

On voit que dans ces conditions, le gain en courant est légèrement diminué, par rapport au cas où R_p = 0,9kΩ. En effet, l’excursion I₂ du courant de collecteur, correspondant aux points C'’ et E’’ qui délimitent l’excursion du point de fonctionnement sur la droite de charge R_p = 1,5kΩ est plus petite que l’excursion I₁ relative aux points C' et E’ et qui correspondaient au cas où R_p = 0,9kΩ.

En examinant les excursions de la tension, on remarquera au contraire, que dans le second cas (R_p = 1,5kΩ) on a un gain de tension plus grand, parce que E₂ est plus grand que E₁. Si l’on augmente encore la valeur de R_p, le gain en courant continue à diminuer, tandis que le gain en tension continue à augmenter. Le gain en puissance, donné comme étant le produit des deux gains ci-dessus augmente jusqu’à atteindre un maximum puis commence à diminuer, comme on a pu le voir dans la leçon théorique 15.

Ceci veut dire, qu’il existe une position de la droite de charge dynamique pour laquelle le gain en puissance est maximum ; ceci signifie qu’à puissance d’entrée égale, on obtient le maximum de puissance possible du signal de sortie.

Il est évident que pour exploiter au maximum le transistor, il convient de le faire travailler dans ces conditions, c’est-à-dire avec la valeur particulière R_Co de la résistance de charge, que l’on obtient avec une valeur bien déterminée du rapport de transformation (n_o).

Afin de se rendre mieux compte de ce qui se passe lorsque l’on augmente de plus en plus la résistance de charge (ou bien en faisant croître le rapport de transformation en laissant R_S constante), il suffit de regarder le graphique de la figure 4.

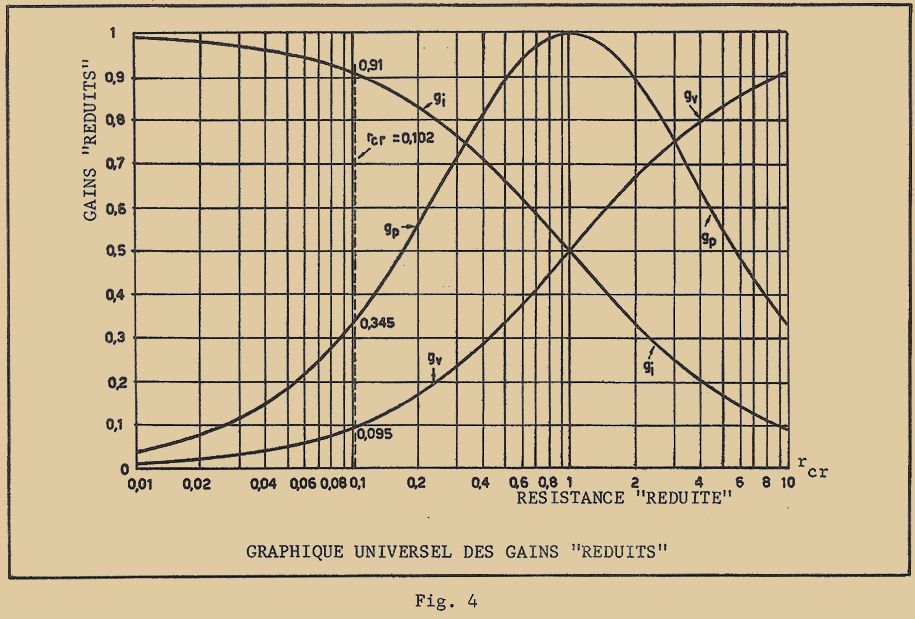
Les courbes qui y sont rapportées, montrent comment varient les gains de courant, de tension et de puissance quand on augmente la valeur de la résistance de charge. Ces résultats ne sont qu’approchés, parce que dans leur calcul, on a négligé l’influence de la tension du collecteur sur la tension de la base (c’est-à-dire que l’on a considéré que le terme h_12e était égal à zéro). Toutefois ces courbes ont l’avantage d’être "universelles", c’est-à-dire qu’elles peuvent servir pour un type quelconque de transistors (transistors BF à faible puissance).

Sur l’échelle horizontale, on a porté les valeurs r_cr de la résistance de charge "réduite" (nous verrons sous peu ce que cela signifie) et croissant de la gauche vers la droite. Les trois courbes sont relatives aux gains "réduits", et respectivement de courant (g_i), de tension (g_v) et de puissance (g_p).

Augmenter la valeur de la résistance de charge signifie se déplacer vers la droite sur l’échelle horizontale : en faisant ainsi, on voit que le gain de courant diminue continuellement, tandis que le gain en tension croît sans cesse, tandis que le gain en puissance augmente jusqu’à un certain maximum, puis diminue, comme on l’a déjà dit.

L’utilisation de ce graphique est très simple. Prenons par exemple le cas de la figure 1, et supposons que l’on désire faire R_p = 1,5 kΩ. Pour le point de repos considéré, c’est-à-dire A’ de la figure 3, les paramètres hybrides du transistor sont ceux que l’on a calculés déjà dans la leçon précédente.

h_11e = 0,77 kΩ  ;  h_21e = 49,5  ;  h_22e = 0,068mA/V

La valeur de h_12e ne nous intéresse pas, puisque nous avons dit que pour ce graphique on supposait que sa valeur était nulle.

Avant tout, on calcule la valeur de la résistance de charge "réduite" qui est donnée par la formule :

r_cr = h_22e x R_p = 0,068 x 1,5 = 0,102

En face de cette valeur lue sur l’axe horizontal (ligne en pointillés sur la figure 4), on peut lire les valeurs suivantes des gains "réduits".

g_i = 0,91  ;  g_v = 0,095  ;  g_p = 0,345

Pour avoir les gains véritables du transistor, il suffira d’utiliser les formules suivantes :

G_i = h_21e x g_i = 49,5 x 0,91 = 45

G_v = h_21e/(h_11e x h_22e) x g_v = 49,5/(0,77 x 0,068) x 0,095 = 945 x 0,095 = 89,8

G_p = (h_21e)²/(4 x h_11e x h_22e) x g_p = (49,5)²/(4 x 0,77 x 0,068) x 0,345 = 11.700 x 0,345 = 4.040

Cette dernière valeur peut naturellement être déduite des deux précédentes :

en effet G_p = G_i x G_v = 45 x 89,8 = 4.040 environ

En comparant ces valeurs avec celles calculées dans la 15^ème leçon théorique (avec R_c = 1,5kΩ) on voit qu’elles sont très voisines entre-elles.

Pour obtenir le maximum de gain en puissance, il suffit donc d’augmenter la valeur de la résistance de charge jusqu’à ce que sa valeur coïncide avec le maximum de la courbe relative à g_p de la figure 4, c’est-à-dire jusqu’à obtenir r_cr = 1.

Comme on dit que r_cr = h_22e x R_p, avoir r_cr = 1, signifie que la valeur optimum de la résistance de charge doit être égale à 1/h_22e, c’est-à-dire qu’elle doit être égale à la valeur de la résistance de sortie du transistor. Dans le cas de l’exemple on aura :

R_Co = 1/0,068 = 14,7 kΩ

Les valeurs correspondantes des gains "réduits" qui peuvent être lues sur le graphique sont :  g_i = 0,5  ;  g_v = 0,5  ;  g_p = 1.

En mettant ces valeurs dans les formules précédentes, on trouve :

G_i = 49,5 x 0,5 = 24,75

G_v = 945 x 0,5 = 472, 5

G_p = 11.700 x 1 = 11.700

Le rapport de transformation nécessaire pour obtenir la valeur optimum de la résistance de charge dynamique sera :

n_o = √(R_Co/R_S) = et dans le cas de notre exemple :

n_o = √(14,7/0,75) = √19,6 = 4,43

Avec un tel rapport de transformation, la résistance d’entrée du second étage est "transformée" en une valeur égale à celle de sortie du premier étage. On dit alors, que le transformateur "adapte" entr’elles les impédances de sortie et d’entrée des deux étages. C'est pour cela, que l’on dit que la condition nécessaire pour avoir un gain maximum en puissance est que la sortie du premier étage soit adaptée (par l’intermédiaire du transformateur) à l’entrée du second étage.

3 – VALEUR MAXIMUM DE LA TENSION DE COLLECTEUR

En examinant la figure 5 (Théorique 17), on voit que la droite de charge dynamique est toujours moins inclinée que la droite de charge statique ; ceci signifie que pendant le fonctionnement (c’est-à-dire pendant une période entière du signal) la valeur de la tension du collecteur (mesurée par rapport à l’émetteur) ne peut jamais atteindre la valeur de la tension d’alimentation V_cc, et ne peut au maximum qu’atteindre la valeur correspondant au point H’.

En effet, si l’on augmente l’amplitude du signal de commande, le point de fonctionnement peut se déplacer au maximum jusqu’au point H’, sui se trouve sur la courbe I_B = 0 et qui correspond au blocage du transistor mais ne peut aller au-delà, c’est-à-dire qu’il peut atteindre au maximum 5,2V environ.

Dans le cas d’un couplage par induction, la droite de charge dynamique peut prendre une inclinaison quelconque, comme on l’a vu et en général elle est plus inclinée (sur l’axe horizontal) que la droite de charge statique.

Le point de fonctionnement peut se déplacer alors jusqu’au point L’ (comme par exemple dans le cas de la figure 3 où R_c = 1,5 kΩ) ce qui signifie que la tension instantanée de collecteur peut atteindre des valeurs plus élevées que la tension même d’alimentation. Dans le cas de l’exemple, elle atteint une valeur presque égale à 9 V, tandis que la tension d’alimentation est de 6 V seulement.

Ce fait, bien étrange à première vue, peut s’expliquer assez facilement si l’on regarde le schéma de la figure 5, dans lequel pour plus de simplicité on a dessiné le transformateur un peu différemment par rapport à la figure 1.

En se rappelant que le courant de collecteur I_C peut être considéré comme étant la résultante de la composante continue de polarisation I_Co et la composante alternative i_C qui change de sens à chaque alternance on peut considérer deux cas :

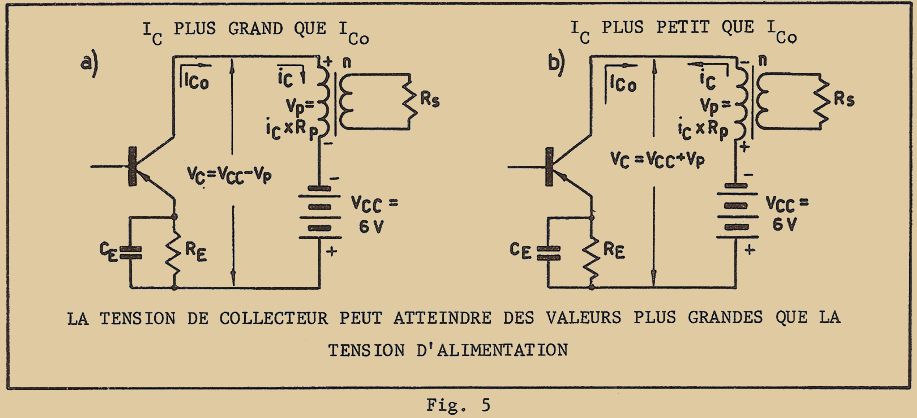
a) Le courant i_C a même direction que I_Co (figure 5-a). La tension V_p aux bornes du primaire (dûe exclusivement au courant i_C, puisque pour I_Co, le primaire se comporte comme une simple liaison) aura pour valeur : V_p = i_C x R_p (puisque pour i_C le transformateur se comporte comme une résistance R_p) et sa polarité sera celle indiquée sur la figure.

On voit donc que la tension V_p se trouve en série avec la tension V_CC de la pile, mais sa polarité est opposée à cette dernière, et ainsi entre le collecteur et la masse, on a une tension V_C égale à V_CC – V_p.

On en déduit que la tension entre le collecteur et la masse est plus petite que la tension d’alimentation. De plus la tension qu’on lit sur l’échelle horizontale de la Fig. 3 n’est pas V_C mais V_CE. Pour obtenir V_CE de la valeur V_C on doit encore soustraire la chute de tension V_E qui se produit aux bornes de R_E : on a donc V_CE = V_C – V_E.

b) Le courant i_C est de sens opposé au courant I_Co (figure 5-b). Ceci arrive pendant l’alternance qui suit la précédente. En changeant le sens de i_C, on inverse la polarité de la tension aux bornes du primaire comme on peut le voir sur la figure 5b. Dans ce cas, la tension entre collecteur et masse n’est autre que la somme de V_CC et de V_p, c’est-à-dire que V_C est obligatoirement plus grande que V_CC, c’est-à-dire qu’elle est plus grande que la tension d’alimentation. La tension V_CE (c’est-à-dire la tension entre collecteur et émetteur donnée sur les caractéristiques du collecteur), sera, comme on l’a vu, un peu plus petite que la tension V_C mais peut normalement atteindre des valeurs plus grandes que la tension d’alimentation.

En conclusion nous dirons, que lorsque la liaison entre les deux étages est du type capacitif, la tension V_CE ne peut pas dépasser la valeur de la tension d’alimentation : lorsque la liaison est du type inductif la tension V_CE la dépasse presque toujours et peut atteindre dans certains cas, le double de V_CC.

On devra donc toujours se rappeler cette possibilité de façon à éviter que pendant le fonctionnement, la tension de collecteur ne puisse dépasser la valeur maximum admise.

Une bonne règle pour le choix de la valeur d’alimentation est la suivante : dans le cas d’une liaison par capacité, la tension d’alimentation ne doit pas être supérieure à la valeur V_CEmax (définie dans la 10ème leçon théorique) ; dans le cas d’une liaison par transformateur, la tension d’alimentation ne doit pas dépasser la moitié de V_CEmax

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 17^ème LEÇON THÉORIQUE

1 – La résistance d’entrée d’un amplificateur à collecteur commun est approximativement β fois la valeur de la résistance de charge.

2 – C'est l’amplificateur à émetteur commun qui donne le plus grand gain en puissance.

3 – Dans un amplificateur en base commune, c’est le gain en tension qui est le plus élevé, étant donné qu’il n’y a pas de gain en courant.

4 – C'est l’amplificateur en base commune qui présente la plus faible résistance d’entrée.

5 – La résistance d’entrée d’un amplificateur à émetteur commun ne dépend pratiquement pas de la valeur de la résistance de charge.

6 – Le condensateur d’émetteur évite pour le signal l’effet de contre-réaction.

7 – La résistance de charge dynamique a pour valeur R_C, et la statique R_C + R_E.

8 – On appelle couplage capacitif, la liaison par capacité qui relie deux étages. Le couplage inductif signifie que les deux étages sont reliés par un transformateur.

9 – La valeur de la résistance de charge dynamique, dans le cas d’un couplage capacitif est donnée par la mise en parallèle de la résistance de collecteur et de la résistance d’entrée de l’étage suivant.

---

EXERCICES DE RÉVISION SUR LA 18^ème LEÇON THÉORIQUE

1 – Qu’est-ce qu’un transformateur idéal ?

2 – Quelles sont les valeurs de la résistance de charge statique et dynamique dans le cas d’une liaison par transformateur ?

3 – Si l’on garde le même point de repos d’un transistor et si l’on augmente la valeur de la résistance de charge, comment varient les gains en tension et en courant ?

4 – Qu’appelle-t-on charge optimum ?

5 – Est-ce que la tension de collecteur peut dépasser la tension d’alimentation ? Si oui, quand ?

6 – La tension collecteur-émetteur maximum d’un certain transistor est 12 V. On veut utiliser celui-ci en liaison capacitive. Quelle est la valeur maximum de la tension d’alimentation que l’on pourra utiliser ?

7 – Lorsque le gain en puissance est maximum, quelles sont les valeurs des gains réduits en tension et en courant ?

8 – Pourquoi faut-il adapter les impédances dans une liaison par transformateur ?

9 – La résistance de charge au secondaire d’un transformateur est 3,5Ω. Le rapport de transformation est n = 25. Calculer la valeur de la résistance que l’on "voit" aux bornes du primaire ?

Fin de la leçon 18

---

LECON 19

1 – AMPLIFICATEURS DE PUISSANCE

Si l'on veut obtenir des puissances de sortie comprises entre quelques dixièmes de watts et quelques watts (puissances nécessaires pour les haut-parleurs des récepteurs allant du type portatif au type auto), il faudra utiliser des transistors de dimensions et de performances plus grandes que ceux vus jusqu'à présent.

Les transistors que nous avons vus jusqu'à présent, pouvaient délivrer des puissances de quelques milliwatts, tout au plus suffisantes pour actionner un écouteur de prothèse auditive (amplificateurs pour sourds).

Les transistors de puissance, comme leur nom l'indique, peuvent au contraire délivrer des puissances notables, mais naturellement, ils nécessitent des puissances de commande beaucoup plus grandes : ainsi un étage de puissance est toujours précédé d'un ou plusieurs étages de "tension" (comme on les appelle en général, d'ailleurs bien improprement) du type de ceux que nous avons étudiés jusqu'à maintenant, et qui peuvent délivrer un signal dont la puissance est suffisante pour piloter l'étage final.

Bien que les étages de puissance ne diffèrent pas dans leur principe de fonctionnement, des étages dits de "tension", ils peuvent être réalisés à l'aide de schémas assez différents lorsque les puissances nécessaires deviennent importantes.

Il faut avant tout remarquer qu'un étage de puissance fonctionne toujours avec des signaux forts pour pouvoir exploiter au maximum les possibilités des transistors. En conséquence l'étude d'un tel amplificateur est faite exclusivement d'après les caractéristiques du transistor, et en général par voie graphique plutôt qu'à l'aide des différents paramètres. Ceci est tellement vrai que pour les transistors de puissance, le constructeur ne donne en général pas les paramètres hybrides ou autres, mais seulement le coefficient d'amplification en courant, pour un certain point de fonctionnement.

Le fonctionnement avec signaux de grande amplitude soulève un premier problème auquel nous avons déjà fait allusion et qui est de très grande importance : il s'agit de la distorsion qui doit être réduite obligatoirement au minimum afin d'obtenir une bonne qualité de reproduction des sons.

Un autre problème, qui avait auparavant une importance moindre, et qui est maintenant devenu primordial, est celui de la dissipation de chaleur dans le transistor. Toujours pour la même raison (exploitation au maximum des possibilités du transistor), on arrive à des puissances dissipées sur le collecteur très voisines des valeurs admissibles.

La température de la jonction n'est plus déterminée exclusivement par la température ambiante, comme cela était le cas pour les transistors étudiés jusqu'à maintenant (pour lesquels on admettait en première approximation, que la température de la jonction était la même que celle de l'ambiante), mais est déterminée par les conditions de fonctionnement du transistor.

Il ne suffit plus maintenant de vérifier que la puissance dissipée ne dépasse pas le maximum permis pour un fonctionnement normal, mais il faut encore apporter une attention toute particulière à la stabilité thermique du circuit afin d'éviter que ne se manifeste le phénomène d'autodestruction du transistor. En effet, un accroissement de la température provoqué par le courant qui traverse le transistor, provoque une augmentation du courant de collecteur ; ceci provoque une augmentation de la puissance dissipée et par voie de conséquence un accroissement de la température : ceci provoque une nouvelle augmentation du courant, puis de la température et le phénomène continue jusqu'à ce que le transistor commence à travailler dans des conditions dangereuses, et se détruise irrémédiablement.

Pour éviter un tel inconvénient, il faut prévoir le montage du transistor de manière qu'il puisse dissiper la chaleur qui se développe à l'intérieur.

Dans certains cas, on est même obligé de monter le transistor sur des plaques en cuivre ou en aluminium, ou bien de placer des ailettes métalliques de refroidissement sur le corps même.

Un troisième problème, qui avait été négligé jusqu'à maintenant est celui du rendement, dont l'importance est très grande pour la détermination de la puissance maximum de sortie ainsi que pour la durée de la pile qui alimente le circuit.

Les problèmes de la distorsion et de la dissipation seront examinés dans les cas particuliers des exemples numériques qui vont suivre, et relatifs aux différents types fondamentaux des étages de puissance. Le problème du rendement par contre, mérite au contraire, d'être traité à part.

Il est bon de préciser avant tout, qu'on peut définir deux rendements différents, selon que l'on considère le transistor seul ou l'étage dans son ensemble. Il faut encore faire la distinction entre l'étage final constitué par un seul transistor et l'étage constitué par deux transistors en opposition de phase (push-pull).

1 – 1 RENDEMENT THÉORIQUE DU TRANSISTOR

Le rendement du transistor est défini comme étant le rapport entre la puissance de sortie P_o du transistor et la puissance P_Co qui est délivrée par la pile d'alimentation. Le rendement est indiqué en général par la lettre grecque η (se lit "éta") : η = P_o/P_Co .

Ce rapport, comme tous les rendements, est toujours plus petit que 1, ce qui signifie que la puissance délivrée par la pile est toujours plus grande que la puissance fournie à la charge ; la différence entre les deux puissances est celle qui est dissipée en chaleur dans le transistor même.

Il est donc évident que plus la puissance délivrée par le transistor est élevée, plus le rendement est grand et plus faible est la chaleur dissipée dans le transistor.

Dans le cas où l'on n'utilise qu'un seul transistor, il n'y a qu'une seule manière possible de réaliser l'étage final : comme nous allons le voir par la suite, il sera du type stabilisé en température et à liaison par transformateur. Son schéma électrique sera donc identique à celui que nous avons étudié dans la précédente leçon, sauf que maintenant le transformateur de sortie sera couplé à une charge (qui est en général constituée par la bobine mobile du haut-parleur) au lieu d'être couplé comme auparavant, à un autre étage.

Dans ces conditions, le transistor travaille en classe A, ce qui signifie que pendant un cycle entier du signal excitateur appliqué à l'entrée de l'étage, le transistor n'est jamais porté au blocage (si cela se faisait, le signal de sortie serait fortement distordu) ; ainsi le transistor conduit pendant la période entière du signal d'excitation et conduit aussi même lorsqu'il n'y a pas de signal.

Le rendement du transistor est donc nul en l'absence du signal d'excitation, puisque, dans ces conditions, il ne fournit aucune puissance (le signal de sortie est nul, la puissance de sortie est nulle aussi P_o = 0), tandis qu'il absorbe une certaine puissance P_Co de la pile d'alimentation.

Quand on applique un signal d'excitation, le transistor délivre une certaine puissance, mais continue toujours à absorber la même puissance de la pile ; le rendement n'est plus nul, mais augmente lorsque croît le signal de commande.

On démontre facilement que l'on a le maximum de rendement du transistor lorsque celui-ci délivre la puissance maximum dont il est capable : dans ce cas, le rendement théorique qu'il peut atteindre est de 0,5 (ou si l'on préfère de 50%). Ce rendement n'est jamais tout à fait atteint en pratique.

Ceci signifie, que si l'on dispose d'un transistor fonctionnant en classe A prévu pour fournir une puissance de 1W (par exemple), il va absorber une puissance P_Co de 2 W sur la pile. Lorsque le transistor ne délivre pas de puissance (signal d'excitation et signal de sortie nuls), cette puissance de 2 W est entièrement transformée en chaleur dans le transistor ; quand le transistor délivre la puissance P_o, la puissance constante P_Co (de 2 W) absorbée de la pile se divise en 2 parties ; l'une constitue P_o, l'autre (égale à la différence P_Co – P_o) n'est autre que la puissance P_C dissipée dans le transistor. Quand le transistor délivre la puissance maximum de 1W la puissance dissipée dans le transistor est réduite à 1W, c'est-à-dire qu'elle est alors minimum.

On peut donc dire que dans un étage fonctionnant en classe A, le transistor "chauffe moins" quand il fournit la puissance maximum, et qu'il "s'échauffe au maximum", quand il ne délivre pas de puissance du tout., c'est-à-dire lorsqu'il ne travaille pas. En d'autres termes, nous dirons que la puissance maximum qu'un transistor peut délivrer (en théorie bien entendu) est égale à la moitié de la puissance maximum qu'il peut dissiper.

Le défaut d'un étage en classe A avec un seul transistor est la distorsion non négligeable qui apparait lorsque la puissance délivrée est voisine de la puissance maximum.

Une réduction très sensible de cette distorsion peut être obtenue en utilisant deux transistors en opposition de phase (ou "push-pull") fonctionnant encore en classe A. Dans ce cas, le rendement maximum est encore de 0,5 (50%) ; la puissance maximum disponible et la puissance délivrée par la pile, sont maintenant le double de celles que l'on avait avec un seul transistor, c'est-à-dire que le seul avantage d'un montage en opposition de phase, par rapport à un étage avec un seul transistor est celui d'obtenir une forte réduction de la distorsion.

Un avantage notable du point de vue du rendement peut être obtenu avec un étage push-pull en classe B.

Pour faire travailler les deux transistors en classe B, il faut les polariser presque à l'interdiction (ou au "cut-off", terme anglais) de façon que l'un conduise (et amplifie) seulement que pendant les alternances positives du signal d'excitation, et que l'autre n'amplifie que pendant les alternances négatives.

De cette façon, on voit tout de suite que le rendement peut être plus élevé que dans les cas précédents, parce que en l'absence du signal les deux transistors sont au cut-off, qu'ils ne délivrent pas de puissance mais aussi qu'ils n'en absorbent pas de la pile.

Ainsi donc, la pile ne fournit de puissance que lorsque les transistors délivrent eux-mêmes de la puissance. On démontre que le rendement maximum théorique des transistors est de 0,785 (78,5%), et qu'il est atteint quand les transistors délivrent la puissance maximum. Ceci signifie que si les deux transistors en classe B, délivrent une puissance maximum de 1 W, la pile ne délivre qu'une puissance de 1/0,785 = 1,275W au lieu de 2W comme dans le cas du montage en classe A.

L'augmentation du rendement, qui se traduit en pratique par une durée plus grande de la pile, a un autre avantage d'une grande importance : pour une même puissance de sortie, on obtient une puissance dissipée dans les transistors plus faible, ou, ce qui revient au même, à égalité de puissance dissipée dans les transistors, on peut obtenir une puissance de sortie plus grande. On démontre que la puissance de sortie maximum que l'on peut obtenir avec une paire de transistors montés en classe B, est égale à près de cinq fois (ou plus exactement à 4,93 fois) la puissance maximum que peut dissiper chacun d'eux.

Ainsi par exemple, si l'on utilise des transistors qui peuvent dissiper chacun une puissance maximum de collecteur P_Cmax de 1watt, la puissance maximum de sortie P_o max que l'on peut obtenir avec un montage push-pull classe B est de 4,93Watts

Tout ce que nous venons de voir a été résumé dans le tableau suivant :

Type de l'étage Final	Rendement théorique	Puissance de sortie maximum (Pomax)
Classe A	0,5 (50%)	0,5 x Pcmax
Push-Pull classe A	0,5 (50%)	Pcmax
Push-Pull classe B	0,785 (78,5%)	4,93 x Pcmax

En examinant les valeurs reportées ci-dessus, nous pourrons noter, qu'en utilisant un type donné de transistor de transistor de puissance, dans un montage push-pull classe A, nous obtenons une puissance de sortie maximum qui est à peine le double de celle que l'on peut obtenir avec un seul transistor, Si nous choisissons au contraire un montage push-pull classe B, la puissance de sortie maximum est presque 10 fois celle que nous avons avec un seul transistor.

Ces considérations, bien que basées sur des valeurs théoriques, qui ne sont jamais atteintes en pratique, permettent de conclure qu'un montage push-pull classe B est beaucoup plus avantageux qu'un montage en classe A. C'est surtout pour cette raison, qu'en pratique on n'utilise que très rarement le push-pull classe A, et nous n'en parlerons pas dans les prochaines leçons.

1 – 2 RENDEMENT RÉEL DU TRANSISTOR ET DE L'ÉTAGE

Les valeurs de rendement que nous venons de voir sont dites "théoriques" en ce sens qu'elles ne sont jamais atteintes en pratique ; ce n'est qu'en montage base à la masse que ces rendements se rapprochent des valeurs théoriques.

En effet, si l'on considère un étage en classe A à un seul transistor (le raisonnement suivant est valable aussi pour les étages push-pull en classe A ou B) on voit d'après la figure 1-a (qui représente le fonctionnement sur les caractéristiques de collecteur pour le montage en base commune) que le point de fonctionnement peut atteindre effectivement les points H et K d'intersection de la droite de charge avec les 2 axes.

Ceci est dû au fait que les caractéristiques de collecteur chutent à gauche de l'axe vertical et parce que la caractéristique correspondant au courant de commande nul (I_E = 0) se confond pratiquement avec l'axe horizontal.

Dans ces conditions, si l'on fait varier le courant de collecteur de zéro à I_Cmax, la tension de collecteur passe de la valeur maximum V_CE max à une valeur minimum V_CEmin qui est zéro ; l'excursion de la tension de collecteur atteint ainsi la valeur maximum possible qui est égale à V_CEmax.

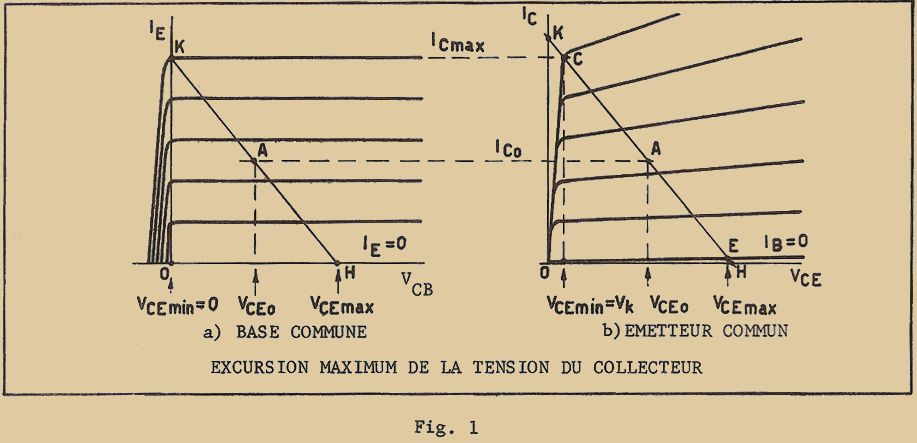
Si l'on considère maintenant un étage en classe A à un seul transistor mais en montage émetteur à la masse, on voit sur la figure 1-b, qui en représente le fonctionnement, que le point de fonctionnement ne peut plus atteindre les points H et K, à cause de la nature même des caractéristiques de collecteur, puisque ces dernières chutent maintenant à droite de l'axe vertical, et que celle qui correspond à I_B = 0 ne coïncide plus exactement avec l'axe horizontal ; l'excursion du point de fonctionnement est limitée à C et E.

Dans le cas des transistors de puissance, le point E est assez voisin du point H et on peut admettre que le point de fonctionnement atteint le point H.

Le point C est par contre nettement différent du point K ; ceci signifie que la tension V_CEmin n'atteint pas la valeur zéro, mais ne peut atteindre au plus que la tension V_K et qui est de l'ordre de 0,5 V.

En conclusion, l'amplitude crête à crête du signal est inférieure à V_CEmax.

A égalité de tension V_CEo et de courant de repos I_Co, la puissance que fournit la pile reste la même dans les deux cas tandis que le signal de sortie (et la puissance de sortie P_o) est évidemment plus faible dans le cas de la figure 1-b, puisque l'excursion de V_C est plus petite. Pour cette raison, le rendement du transistor est encore plus faible en montage émetteur commun.

Si l'on suppose par exemple que la tension d'alimentation V_CC est de 9 V et que V_k est de 0,5 V, le rendement est réduit dans le rapport

(V_CC-V_k)/V_CC  = (9-0,5)/9 = 8,5/9 = 0,944 environ

Pour le montage en émetteur commun, nous aurons donc les rendements maxima suivants :

Classe A : 0,5 x 0,944 = 0,472 (c'est-à-dire 47,2% au lieu de 50%)

Classe B ; 0,785 x 0,944 = 0,74 (c'est-à-dire 74% au lieu de 78,5%)

Ces valeurs sont cependant des valeurs maxima des rendements réels que l'on peut obtenir en pratique, quand les transistors sont montés en émetteur commun.

La puissance de sortie P_o délivrée par le transistor (ou par les deux transistors) ne pourra jamais être totalement utilisée dans la charge (haut-parleur) à cause de la présence du transformateur de sortie, qui en pratique n'est jamais "idéal", et aussi à cause de la résistance d'émetteur placée pour la stabilisation thermique.

Le rendement de l'étage est par conséquent toujours plus faible que le rendement calculé pour le transistor seul, à cause des pertes inévitables dans le transformateur et dans la résistance d'émetteur.

Le rendement de l'ensemble est indiqué par η_s et est défini comme étant le rapport entre la puissance P_u effectivement délivrée à la charge (puissance utile) et la puissance P_CC que l'étage absorbe sur la pile :

η_s = Pu/P_CC

Comme nous le verrons sur des exemples numériques, le rendement de l'étage peut-être notablement inférieur au rendement du transistor lorsque l'on utilise des transformateurs de sortie ayant des enroulements assez résistants et une résistance d'émetteur élevée.

2 – AMPLIFICATEUR DE PUISSANCE CLASSE A

Le schéma type d'un étage de sortie, ou de puissance est indiqué à la figure 2. Comme on peut le voir, il s'agit d'un étage à émetteur commun avec stabilisation thermique, et couplé à la charge (ou au haut-parleur) par l'intermédiaire d'un transformateur. La charge est représentée sur la figure 2 par la résistance R_S dont la valeur est égale à l'impédance du haut-parleur, valeur en général indiquée par le constructeur du H.P.

Le transistor choisi dans notre exemple est un SFT 125. Ce transistor peut être utilisé dans les amplificateurs de faible puissance, comme par exemple ceux utilisés dans les récepteurs portables.

Les valeurs limites sont les suivantes :

• tension maximum de collecteur :
  V_CEmax = 20 V
• courant maximum de collecteur :
  I_Cmax = 300mA
température maximum de la jonction :
Tj max = 75°C résistance thermique (avec ailette de refroidissement) :
K = 0,09° C/mW
• courant résiduel de collecteur à 25°C :
  I_CBo inférieur à 20µA
tension de collecteur minimum :
V_k = 0,5 V coefficient d'amplification en courant :
β = 100

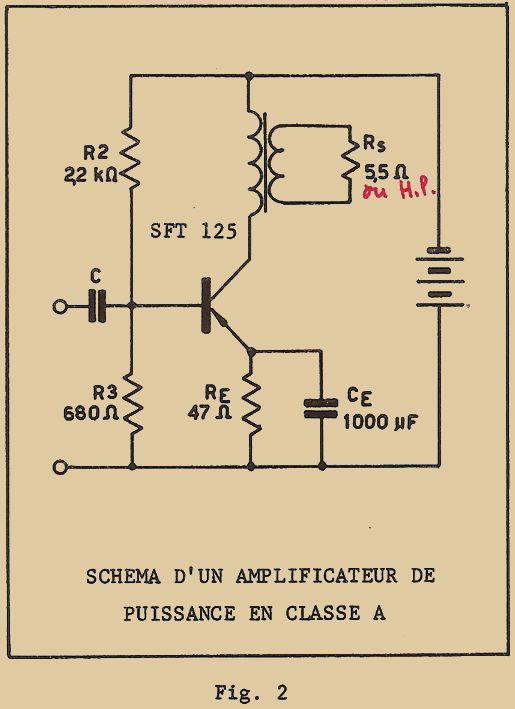
Nous en déduirons, selon ce qui a été dit dans la leçon théorique 10, que la puissance maximum P_Cmax que l'on peut dissiper sur le collecteur afin que la température de la jonction ne dépasse pas la valeur maximum permise est : (pour une température ambiante de 45° C)

P_Cmax = (T(j max) - Ta)/K = (75-45)/0,09 = 30/0,09 = 333mW

Pour plus de sécurité, nous arrondirons cette valeur à 300mW

Nous avons maintenant tous les éléments, pour tracer sur les caractéristiques la courbe de dissipation maximum, la droite de charge et le point de fonctionnement.

2 – 1 DROITE DE CHARGE

Pour tracer les droites de charge statique et dynamique, il faut encore tenir compte de la résistance des enroulements du transformateur de sortie : le transformateur réel va donc se présenter comme sur la figure 3-a. On peut donc considérer le transformateur réel, comme un transformateur idéal (ayant le même rapport de transformation) mais qui aurait en série avec les enroulements primaire et secondaire, les résistances r_p et rs ; ces résistances devront avoir pour valeur la résistance des enroulements du transformateur réel.

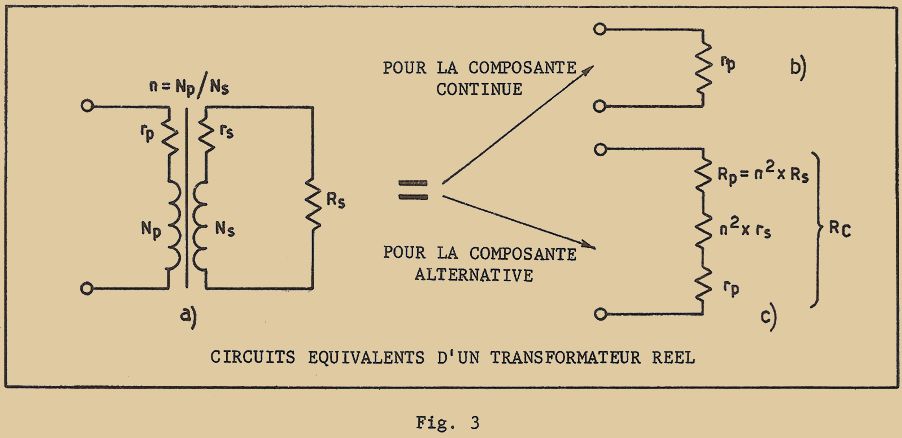
En se rappelant ce qui a été dit dans la leçon précédente, on peut déduire immédiatement les schémas équivalents du transformateur réel, pour le courant continu et pour le courant alternatif, quand le secondaire est fermé sur la charge R_S.

En observant la figure 3-a, on voit que pour le courant continu, le transformateur se comporte comme une résistance de valeur r_p (figure 3-b).

En ce qui concerne le courant alternatif, il se comporte comme une résistance R_C (figure 3-c) constituée par la mise en série de trois résistances : R_p égale à R_S x n² qui représente la charge ramenée au primaire (de la même façon que pour un transformateur idéal) ; rs x n² qui représente la résistance du secondaire ramenée au primaire ; r_p qui est la résistance du primaire.

Supposons que r_p = 10Ω, la valeur de la résistance de charge statique qui résulte du schéma de la figure 2 sera :

R_st = r_p + R_E = 10 + 47 = 57Ω

En alimentant le circuit par une tension de 9V, la droite de charge statique passera par le point de l'axe horizontal correspondant à V_CC = 9V et par le point de l'axe vertical correspondant à un courant :

I_CC = V_CC/R_st  = (9 V)/57 = 0,158 A = 158mA

Sur cette droite, on fixera le point de fonctionnement A' (figure 4). Pour exploiter au maximum le transistor, le point A' sera placé le plus près possible de la courbe de dissipation maximum. On pourrait à la limite le placer exactement sur cette courbe, auquel cas, la puissance dissipée sur le collecteur serait égale au maximum permis de 300mW. Mais il faut tenir compte de ce que les caractéristiques sont tracées pour une température ambiante de 25° C, et qu'elles sont susceptibles de se déplacer vers le haut quand la température augmente avec comme risque de déplacer le point A' au-dessus de la courbe de dissipation maximum.

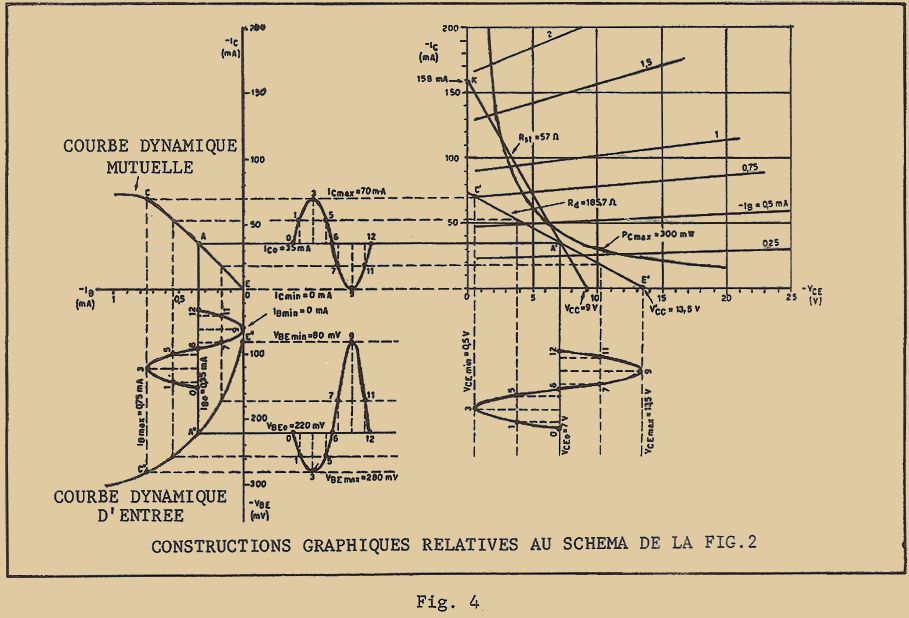
Afin d'éviter cet inconvénient qui aurait comme conséquence la destruction définitive du transistor, il est bon de placer le point A' un peu au-dessous de la courbe de dissipation maximum, comme sur la figure 4.

Dans ces conditions, la tension et le courant de repos sont respectivement V_CEo = 7 V et I_Co = 35mA ; la puissance dissipée sur le collecteur est :

P_C = V_CEo x I_Co = 7 x 35 = 245mW

c'est-à-dire un peu inférieure à P_Cmax = 300mW

Il faut maintenant tracer la droite dynamique. Pour obtenir une puissance de sortie maximum, il faut faire passer la droite de charge dynamique par le point E' qui se trouve sur l'axe horizontal en correspondance avec la tension V'_CC = 2 V_CEo – V_k = (2 x 7) – 0,5 = 13,5 V (figure 4).

A une telle droite de charge correspond une résistance de charge dynamique égale à :

R_d = (V'_CC - V_CEo)/I_Co  = (13,5 -7)/35 = 6,5/35 = 0,1857kΩ = 185,7Ω

En examinant le schéma de la figure 2, on voit que la résistance dynamique correspond à la seule résistance R_C présentée par le transformateur car R_E est court-circuitée par le condensateur C_E de 1.000 pF.

Pour obtenir cette valeur de R_d avec une charge au secondaire R_s de 5,5Ω, une résistance r_s de l'enroulement secondaire de 1,5Ω et une résistance r_p de 10Ω, le transformateur de sortie devra avoir un rapport de transformation n de :

n = √((R_d-r_p)/(R_s+r_s )) = √((185,7-10)/(5,5+1,5)) = √(175,7/7) = √25,1 = 5,01

Cette valeur pourra être arrondie, dans la pratique à 5, ce qui veut dire que le primaire devra avoir 5 fois plus de spires que le secondaire.

Avec la droite de charge dynamique, on voit que la tension maximum atteinte par le collecteur pendant le fonctionnement est 13,5V (point E') et que le courant maximum de collecteur est 70mA (point C').

Ces valeurs ne dépassent pas les valeurs maxima indiquées précédemment (20V et 300mA) ; il n'y a donc aucun danger pour le transistor.

2 – 2 PUISSANCE ET RENDEMENT

Pour déterminer la puissance maximum P_o, que le transistor peut délivrer, il suffit d'examiner la figure 4 :

V_CEmax = V'_CC = 13,5 V et V_CEmin = V_k = 0,5 V

On détermine alors les valeurs maximum et minimum du courant de collecteur :

I_Cmax = 70mA et I_Cmin = 0mA

La puissance maximum que peut délivrer le transistor est donc :

P_o = ((V_CEmax-V_CEmin ) x (I_Cmax-I_Cmin))/8 = ((13,5-0,5) x (70-0))/8 = (13 x 70)/8 = 910/8  = 114mW

Le transistor absorbe de la pile une puissance P_Co, qu'il délivre ou non lui-même de la puissance. Au repos, P_Co = 245mW. Le rendement η est donc :

η = P_o/P_Co  = 114/245 = 0,465 (soit 46,5% au lieu de 50%)

La puissance Pu fournie à la charge est plus petite que P_o délivrée par le transistor à cause des pertes dans le transformateur dûes à la résistance des enroulements. Pu est donnée par la formule :

P_u = P_o x R_p/R_d

où R_p est la résistance de charge R_s ramenée au primaire et qui est égale à R_C x n² et R_d la résistance de charge dynamique tracée sur les caractéristiques. On devra évidemment exprimer ces deux résistances dans les mêmes unités, c'est-à-dire en Ω ou en kΩ.

Dans notre exemple R_s = 5,5 et n = 5. D'où :

R_p = 5,5 x (5)2 = 5,5 x 25 = 137,5

Comme R_d = 185,7Ω on aura :

P_u = P_o x R_p/R_d  = 114 x 137,5/185,7 = 114 x 0,74 = 84,4mW

On peut maintenant calculer le rendement de l'étage en divisant P_u par la puissance P_CC fournie par la pile. Cette dernière peut être facilement calculée en sachant que la pile a une tension V_CC de 9 V et qu'elle délivre un courant égal à celui qui est absorbé par l'étage final soit I_Co ; on a donc :

P_CC  = V_CC x I_Co = 9 x 35 = 315mW

Le rendement de l'étage est donc :

η_t = P_u/P_CC = 84,4/315 = 0,268 (soit 26,8%)

On voit donc ainsi que le rendement pratique d'un étage est beaucoup plus faible que le rendement théorique du transistor seul.

2 – 3 CIRCUITS DE POLARISTION ET GAINS

Pour que le point de repos vienne en A' (figure 4) le courant de polarisation de la base devra être de 0,35mA comme on peut le voir sur la figure.

Cette valeur est obtenue avec le circuit de polarisation de la figure 2, avec R_E = 47Ω, R₂ = 2,2 kΩ et R₃ = 680Ω.

Pour être certain qu'il n'y a pas de danger d'autodestruction du transistor quand celui-ci fonctionne à la température maximum prévue (T_amb = 45° C), il reste encore à contrôler que le coefficient de stabilité S du circuit reste inférieur à la valeur S_max (donnée par la formule ci-dessus et valable pour des transistors de puissance au germanium quelconque).

S_max = 450/(V_CC x K x I_CBo)

où V_CC est la tension d'alimentation de la pile en volts, K est la résistance thermique du transistor exprimée en °C/mW et I_CBo est la valeur maximum que peut atteindre le courant résiduel du collecteur à la température de 25°C et exprimée en µA.

Dans le cas de l'exemple on trouve avec V_CC = 9V, K = 0,09°C/mW et I_CBo = 20µA.

S_max = (450)/(9 x 0,09 x 20) = 450/16,2 = 27,8 environ

Le coefficient de stabilité du circuit est calculé à l'aide de la formule vue en son temps, avec R_E = 47Ω, R_B = 500Ω (R_B est donné, rappelons-le, par la mise en parallèle de R₂ et R₃) et β = 100.

S = (R_E+ R_B)/(R_E + R_B/β ) = (17 + 500)/(47 + 500/100) = 547/52 = 10,5

Cette valeur de S est nettement inférieure à S_max et nous sommes ainsi sûrs que le circuit est stable du point de vue thermique et qu'il n'y a pas de danger d'autodestruction. Si S n'avait pas été inférieur à Smax, on aurait été obligé de diminuer les valeurs de R₂ et R₃, ou bien augmenter R_E de façon à réduire la valeur de S.

Pour compléter l'étude de l'amplificateur pris comme exemple, il faut encore déterminer les valeurs du courant de commande et de la résistance d'entrée, de façon à pouvoir calculer l'étage précédent (c'est-à-dire le préamplificateur ou l'étage driver).

Dans ce but, on trace dans le deuxième quadrant, la caractéristique mutuelle de courant, relative à la droite de charge dynamique du 1^er quadrant (pour R_d = 185,7Ω – figure 4).

On trouve ainsi, en procédant à la construction inverse de celle de la leçon précédente, la forme du courant de base dont l'excursion est de 0,75mA.

La résistance d'entrée sera calculée si l'on connait l'excursion correspondante de la tension de base. On trouve :

r_B = (V_BEmax - V_BEmin)/(I_Bmax - I_Bmin) = (280-80)/(0,75-0) = 200/0,75 = 266Ω

A remarquer que le résultat est exprimé en ohms, car la tension l'est en mV et le courant en mA.

Pour obtenir la puissance de sortie maximum, l'étage de la figure 2 a besoin d'un courant de commande de 0,75mA d'excursion ; d'autre part, sa résistance moyenne d'entrée est de 266Ω. On peut encore dire que pour délivrer la puissance de sortie maximum l'étage nécessite une puissance de commande (ou puissance d'entrée) P_e de :

P_e = (V_BEmax - V_BEmin) x (I_Bmax - I_Bmin))/8 = ((280 - 80) x (0,75 - 0))/8 = (200 x 0,75)/8 = 18,75 µW

P_e est exprimé en µW, car la tension est donnée en mV et le courant e nmA. Cette puissance devra être fournie par l'étage driver dont la charge est précisément la résistance d'entrée calculée ci-dessus.

Si nous voulons maintenant déterminer le gain en puissance de l'étage considéré, il suffira de faire le rapport entre la puissance P_u et la puissance P_e, toutes les deux exprimées dans les mêmes unités de mesure, par exemple en µW. On trouve, avec P_u = 84,4mW = 84.400 µW.

G_p = P_u/P_e  = 84.400/18,75 = 4.500 environ

Il faut encore remarquer, que ce n'est pas le gain maximum que l'on peut obtenir avec le transistor considéré, parce que, répétons-le la valeur de la droite de charge dynamique a été choisie pour obtenir la puissance de sortie maximum et non pas le gain maximum. Si l'on avait voulu obtenir le gain de puissance maximum, on aurait procédé comme avec les amplificateurs de tension, c'est-à-dire que l'on aurait choisi une valeur de R_d égale à la valeur de la résistance de sortie du transistor.

On voit facilement dans l'exemple, que la valeur de R_d aurait été beaucoup plus grande que la valeur choisie : la puissance de sortie aurait été alors nettement réduite. Dans ces conditions, le transistor de puissance n'aurait pas été bien utilisé : on préfère donc renoncer au maximum de gain en faveur du maximum de puissance de sortie.

L'inconvénient qui en découle est qu'il faut dépense une puissance plus grande pour piloter le transistor final ; mais comme cette puissance est toujours très faible par rapport à la puissance de sortie (un peu plus de 18µW dans le cas de l'exemple), il vaut mieux dépenser quelques dizaines de µW de plus que de renoncer à des centaines de mW de puissance de sortie.

2 – 4 DISTORSIONS

Dans les constructions de la figure 4, nous sommes partis d'une tension et d'un courant de collecteur parfaitement sinusoïdaux comme on les désire en général dans la pratique.

En observant la figure, nous voyons que pour obtenir un courant de collecteur sinusoïdal, c'est-à-dire sans distorsions, le courant de commande de la base devra avoir une allure légèrement différente d'une sinusoïde.

En effet, les deux alternances du courant de base ne sont pas égales : l'une a une amplitude de 0,35mA, l'autre de 0,4mA.

Pour obtenir un courant de collecteur (et donc une tension de collecteur) sans distorsions, il est donc nécessaire de piloter l'étage par un courant de base "convenablement distordu". Ceci n'est pas possible en général ; nous en concluerons qu'en pilotant l'étage par un courant sinusoïdal, le courant de collecteur sera légèrement distordu comme nous l'avons déjà vu dans la 15^ème leçon théorique, parce que la caractéristique mutuelle de courant du deuxième quadrant n'est pas rectiligne, mais incurvée dans sa partie supérieure.

En pilotant l'étage avec un courant de base sinusoïdal dont les deux alternances ont une amplitude de 0,35mA, nous oyons sur la figure 5-a que les alternances du courant de collecteur ne sont pas égales : l'alternance supérieure a une amplitude de 30mA, l'autre de 35mA.

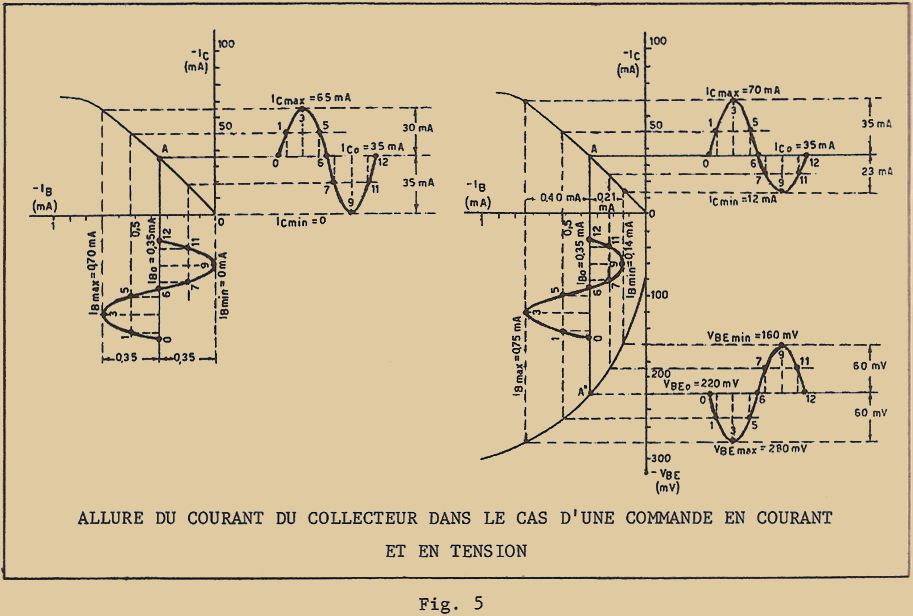
Si l'on pilote au contraire l'étage par une tension sinusoïdale avec une amplitude de 60mV, on obtient la construction de la figure 5-b, où le courant de collecteur est encore distordu ; maintenant au contraire l'alternance négative est de 23mA, et l'alternance positive de 35mA.

Dans ce dernier cas (commande en tension), le courant de base est déjà distordu du fait de la courbure de la caractéristique d'entrée (courbe du troisième quadrant) ce qui fait que l'alternance inférieure est plus petite que l'alternance supérieure. L'alternance supérieure est de 0,40mA, l'inférieure de 0,21mA seulement.

En comparant les formes du courant de base de la figure 5-b, avec celles de la figure 4, on voit que l'on peut faire en sorte d'exploiter la courbure de la caractéristique d'entrée ; ainsi, si l'alternance inférieure du courant de base est de 0,35mA au lieu de 0,21mA, les deux alternances du courant de collecteur auront même amplitude, c'est-à-dire précisément 35mA.

En d'autres termes, la distorsion introduite par la courbure de la caractéristique d'entrée, et celle introduite par la caractéristique mutuelle peuvent se compenser mutuellement, de telle façon qu'en commandant l'étage par une tension sinusoïdale, les deux alternances du courant de collecteur gardent encore la même amplitude. Ceci ne signifie pas que l'on élimine complètement la distorsion du courant de collecteur, mais qu'on la réduit notablement, c'est-à-dire pratiquement au minimum.

Pour comprendre comment il est possible de compenser les deux distorsions introduites, reprenons l'examen de la forme du courant de base de la figure 4, c'est-à-dire celle qui est nécessaire pour obtenir un courant de collecteur avec les deux alternances égales, et procédons comme indiqué à la figure 6.

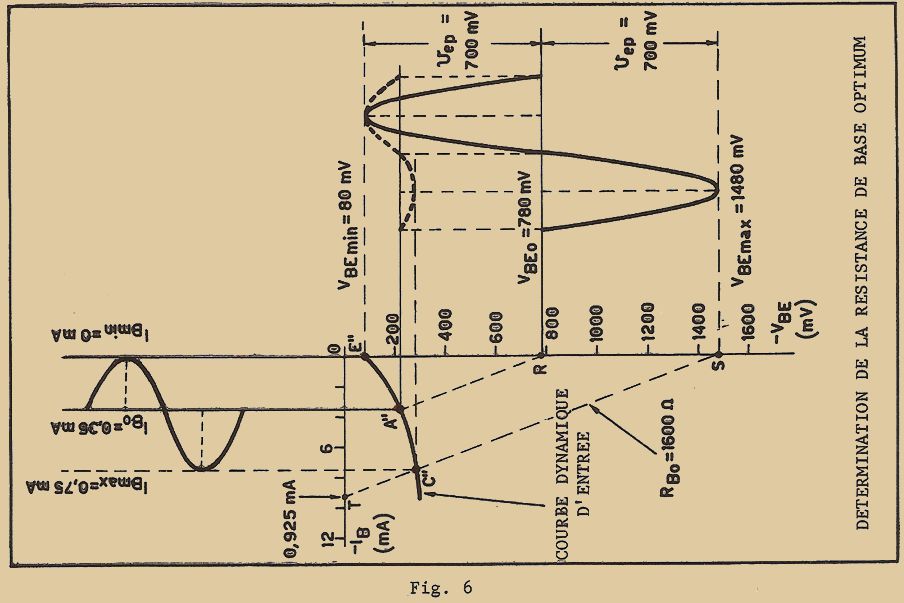
Partons des points A'' et C'', et au lieu de tracer des droites horizontales pour déterminer les valeurs correspondantes de la tension de base et sa forme relative (tracée en pointillés) traçons des droites inclinées de telle manière que le point R soit exactement au milieu de E''S, c'est-à-dire que l'on ait : R_E'' = R_S.

Dans le cas de notre exemple nous trouvons :

distance entre R et E'' = V_BEo – V_BEmin = 780 – 80 = 700mV

distance entre R et S = V_BEmax – V_BEo = 1.480 – 780 = 700mV.

Pour voir quelle est la signification physique de cette droite inclinée il suffit de comparer le troisième quadrant (figure 6) et le premier quadrant de la figure 4. Dans ce dernier, sont reportés la tension et le courant de collecteur et on voit qu'une droite inclinée qui coupe les deux axes représente une résistance de charge, c'est-à-dire une résistance qui dans le schéma électrique est placée en série avec le collecteur.

Dans le cas du troisième quadrant, sont reportés la tension et le courant de base ; on en déduit qu'une droite inclinée qui coupe les deux axes comme sur la figure 6 représente une résistance qui dans le circuit électrique se trouve en série dans la base.

En conclusion, la construction graphique de la figure 6 a la signification suivante : on peut réduire au minimum la distorsion du courant (et de la tension) de sortie en plaçant en série avec la base une résistance R_Bo comme indiqué dans le schéma de la figure 7.

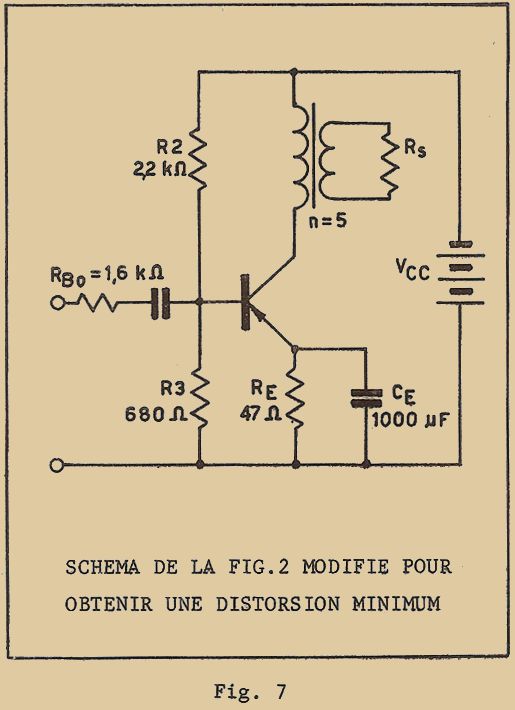
On peut déterminer la valeur d'une telle résistance en faisant le rapport entre la tension et le courant lus aux intersections de la droite et des axes.

Dans le cas de l'exemple, on peut prendre les points d'intersection S et T ; en ces points, on lit 1.480mV (point S) et 0,925mA (point T). La valeur de R_Bo sera en Ω si la tension est exprimée en mV et le courant en mA.

R_Bo = 1.480/0,925 = 1.600Ω

La tension sinusoïdale qui doit être appliquée à l'entrée de l'étage à travers la résistance R_Bo doit, naturellement avoir 700mV d'amplitude (figure 6).

La réduction de la distorsion ainsi obtenue doit être payée par la nécessité de piloter l'étage par une tension d'amplitude plus grande. En effet, on avait besoin avant, d'une excursion totale de la tension de base de 200mV, maintenant, on a besoin d'une excursion de

V_BEmax – V_BEmin = 1.480 – 80 = 1.400mV c'est-à-dire 7 fois plus.

La puissance nécessaire pour piloter le transistor est aussi 7 fois plus grande maintenant :

P_e = (V_BEmax - V_BEmin ) x (I_Bmax - I_Bmin))/8 = ((1.480 - 80) x (0,75 - 0))/8 = (1.400 x 0,75)/8 = 1.050/8  = 131,25µW

au lieu de 18,75 µW comme calculé précédemment. Il est quand même profitable de dépenser un peu plus de puissance pour commander le transistor (on n'a besoin au fond que de quelques dizaines de µW en plus) et réduire ainsi notablement la distorsion du signal de sortie.

Il faut encore remarquer que lorsque l'étage final est commandé par un étage driver, amplificateur de tension comme c'est presque toujours le cas, la résistance R_Bo peut être constituée totalement ou en partie par la résistance de sortie même de l'étage pilote. On fait alors en sorte que cette résistance de sortie ait précisément la valeur de R_Bo nécessaire à la réduction de la distorsion de l'étage final.

Dans l'exemple de l'étage final classe A considéré aujourd'hui, le couplage entre celui-ci et l'étage pilote, peut être indifféremment capacitif ou inductif, selon les schémas vus dans la précédente leçon, étant donné les faibles puissances nécessaires pour la commande.

Dans le cas de l'étage de puissance de sortie plus grande, il est au contraire plus avantageux d'utiliser un transformateur de liaison.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 18^ème LEÇON THÉORIQUE

1 – Un transformateur idéal équivaut à un conducteur sans résistance pour le courant continu et une résistance à n² fois la valeur de la résistance sur laquelle est fermé le secondaire pour le courant alternatif.

2 – Dans le cas d'une liaison par transformateur, la résistance de charge en statique a pour valeur R_E et en dynamique R_p = n² x R_s.

3 – Si l'on augmente la résistance de charge en dynamique, le gain en tension augmente, tandis que celui en courant diminue.

4 – On appelle charge optimum celle qui donne le gain maximum en puissance.

5 – Oui, dans le cas d'une liaison par transformateur.

6 – La liaison étant capacitive, on pourra prendre une tension d'alimentation au plus égale à 12 V.

7 – Lorsque le gain en puissance est maximum, on trouve sur les courbes universelles, que le gain réduit en tension est égal au gain réduit en courant g_i = g_v = 0,5

8 – Si l'on désire obtenir un gain maximum en puissance, on doit chercher à adapter les impédances dans une liaison par transformateur.

9 – La résistance au primaire est :

R_p = n² x R_s = (25)² x 3,5 = 2.200Ω environ.

---

EXERCICES DE RÉVISION SUR LA 19^ème LEÇON THÉORIQUE

1 – Comment définit-on le rendement d'un transistor ?

2 – Quelles sont les valeurs maxima théoriques du rendement d'un transistor ?

3 – Les transistors d'un étage de sortie "chauffent-ils" plus quand l'étage est excité, ou quand il ne l'est pas ?

4 – Quelle est la puissance maximum que peut délivrer un transistor en classe A ou bien deux transistors en classe B, en fonction de la puissance maximum que peut dissiper chacun d'eux ?

5 – Pourquoi le rendement d'un étage est-il toujours inférieur à celui du transistor seul ?

6 – Comment peut-on représenter un transformateur réel ?

7 – Quel est le schéma équivalent d'un transformateur réel, vis-à-vis du courant continu ?

8 – Comment peut-on écarter le danger d'autodestruction d'un transistor de puissance ?

9 – Comment peut-on diminuer au minimum les distorsions d'un étage en classe A constitué par un seul transistor ?

Fin de la leçon 19

---

LECON 20

1 – AMPLIFICATEURS DE PUISSANCE PUSH-PULL

Les amplificateurs de puissance en push-pull sont constitués par 2 transistors qui amplifient 2 signaux parfaitement égaux, mais en opposition de phase (c’est-à-dire déphasés de 180°). Ceci signifie, comme nous le verrons mieux par la suite, que les 2 signaux appliqués sur les bases des 2 transistors sont à tout instant, d’amplitude égale, mais tandis que l’un est positif par rapport à la masse, l’autre est négatif, ou inversement.

Le système est donc parfaitement symétrique, ou plutôt, équilibré par rapport à la masse ; par rapport à un système non équilibré, comme le sont tous les étages qui n’utilisent qu’un seul transistor, on obtient un avantage sensible en ce qui concerne la distorsion du signal de sortie.

En effet, à cause de la symétrie du système (comme nous allons le voir sous peu avec les constructions graphiques relatives à un étage push-pull) le signal de sortie est "symétrique", c’est-à-dire que les 2 alternances du signal de sortie sont parfaitement égales, non seulement en amplitude mais aussi en forme.

Comme nous l’avons vu dans la dernière leçon, ce résultat (égalisation des 2 alternances du signal de sortie) est difficilement obtenu avec un seul transistor, à cause de la courbure de la caractéristique d’entrée ; ce n’est que dans certaines conditions de commande du transistor que l’on peut obtenir 2 alternances d’égale amplitude.

Dans le cas d’un étage push-pull, ce résultat est obtenu automatiquement avec une réduction importante de la distorsion. L’étage push-pull est donc par sa nature même, un circuit de "plus haute qualité" que celui qui n’a qu’un transistor.

Il a en plus d’autres avantages en ce qui concerne le rendement et la puissance absorbée sur la pile d’alimentation, lorsqu’il s’agit d’un étage fonctionnant en classe B.

Comme le fonctionnement d’un étage push-pull classe B est très différent des étages vus jusqu’à présent, il est bon d’étudier son comportement ainsi que les propriétés d’un tel circuit, avant de passer à un exemple numérique avec les constructions graphiques sur les caractéristiques.

Nous allons voir 3 types différents d’étage push-pull classe B : 2 de ceux-ci sont normalement utilisés en pratique, soit dans les récepteurs dont la puissance de sortie n’est pas inférieure à une centaine de milliwatts, soit dans les amplificateurs de puissance plus grande. Le 3^ème type sera étudié surtout pour son intérêt théorique.

1 – 1 ÉTAGE DE SORTIE EN CLASSE B AVEC TRANSFORMATEUR DE SORTIE

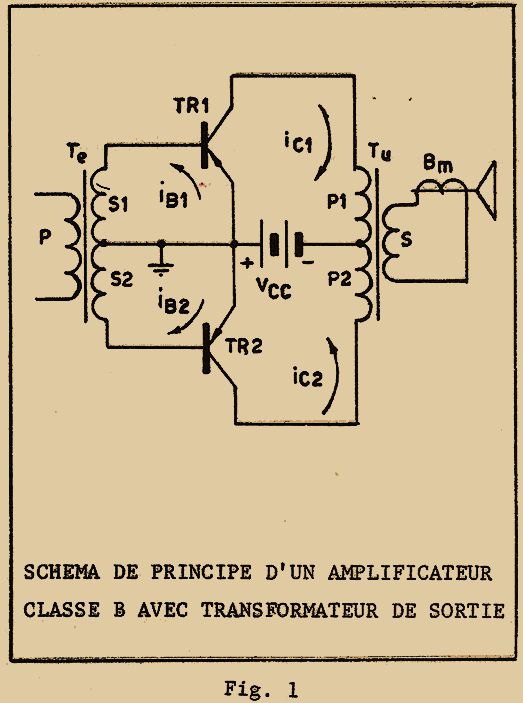
A la figure 1, est indiqué le schéma de principe d’un étage de puissance push-pull classe B avec transformateur de sortie ; les émetteurs des 2 transistors sont directement reliés à la masse (pour simplifier nous ne considérons pour le moment aucun circuit de stabilisation thermique).

La prise centrale du secondaire du transformateur d’entrée est directement reliée à la masse, tandis que les enroulements sont branchés directement sur les bases ; les collecteurs sont alimentés par une seule pile, à travers les 2 enroulements P1 et P2 des primaires du transformateur de sortie.

Le secondaire S de ce transformateur alimente la bobine mobile B_m du haut-parleur qui constitue la charge de l’étage.

La pile d’alimentation est reliée entre la masse et la prise centrale du transformateur de sortie, comme on le voit sur la figure 1.

Si les transistors sont du type PNP, le plus de la pile sera relié à la masse (cas de la figure 1). Dans le cas de transistors NPN, le schéma reste identique mais la pile devra alors avoir son pôle moins relié à la masse.

Le schéma de la figure 1 est relatif au montage en émetteur commun, car c’est celui qui est le plus utilisé dans les récepteurs radio ; tout ce qui sera dit dans les paragraphes suivants reste évidemment valable s’il s’agit du montage base à la masse, compte tenu des quelques différences déjà examinées plusieur_s fois, existant entre les 2 types de montage.

Pour étudier le fonctionnement du schéma de la figure 1, nous allons tout d’abord considérer qu’aucun signal n’est appliqué pour le moment au primaire P du transformateur d’entrée T_e, c’est-à-dire que l’étage est actuellement au repos. On voit que, dans ces conditions, les 2 transistors ne conduisent pas : en effet les 2 émetteurs sont reliés directement à la masse, ainsi que les 2 bases à travers la faible résistance des enroulements S1 et S2 du secondaire du transformateur d’entrée T_e.

De cette manière, les jonctions base-émetteur ne sont pas polarisées, aucun courant ne traverse la liaison de base, et par conséquent, le courant du collecteur est nul. Ainsi, en l’absence d’un signal, les 2 transistors ne conduisent pas (ils sont bloqués) et n’absorbent donc aucun courant de la pile.

Lorsque l’on applique un signal au primaire P de T_e, le comportement du circuit est différent selon qu’il s’agit d’une ou de l’autre alternance ; il faut donc considérer séparément le fonctionnement pour l’alternance positive, puis pour l’alternance négative.

Supposons tout d’abord que l’on applique au primaire de T_e l’alternance négative du signal (qui par simplification est supposé être sinusoïdal mais le raisonnement reste valable pour une forme quelconque du signal). Dans ces conditions, le primaire P est parcouru par le courant i_e avec le sens indiqué sur la figure 2a.

Par induction, le courant i_e induit dans les 2 enroulements secondaires S1 et S2, deux f-é-m (force électromotrice) V_B1 et V_B2 (d’où les courants i_B1 et i_B2 ).

Étant donné la disposition des circuits, la f-é-m V_B1 a le sens de la flèche de l’émetteur de TR₁, tandis que la f-é-m V_B2 a le sens opposé à la flèche de l’émetteur de TR₂.

Si l’on se rappelle la signification de la flèche de l’émetteur (celle-ci indique le sens dans lequel la jonction base-émetteur conduit), on voit que tandis que V_B1 a le sens de conduction de la jonction base émetteur de TR₁, V_B2 a le sens opposé à la conduction de la jonction base émetteur de TR₂.

Le résultat est le suivant : le courant i_B2 ne peut pas circuler ; tout se passe comme si TR₂ n’avait pas de courant de commande ; TR₂ reste donc bloqué pendant toute l’alternance négative du signal de commande appliqué au primaire P. Le courant de collecteur i_C2 reste donc nul.

Le contraire se produit pour TR₁ : dans sa liaison de base, circule le courant i_B1 , et le circuit du collecteur va être traversé par le courant i_C1 , qui aura même forme que i_B1 et sera β fois plus grand que celui-ci (β coefficient d’amplification du courant).

Le courant i_C1 circule dans la moitié P1 du transformateur de sortie T_u avec le sens indiqué sur la figure 2a. Dans le secondaire et dans la charge R_C circulera le courant d’utilisation i_u avec comme sens, celui de la figure 2a.

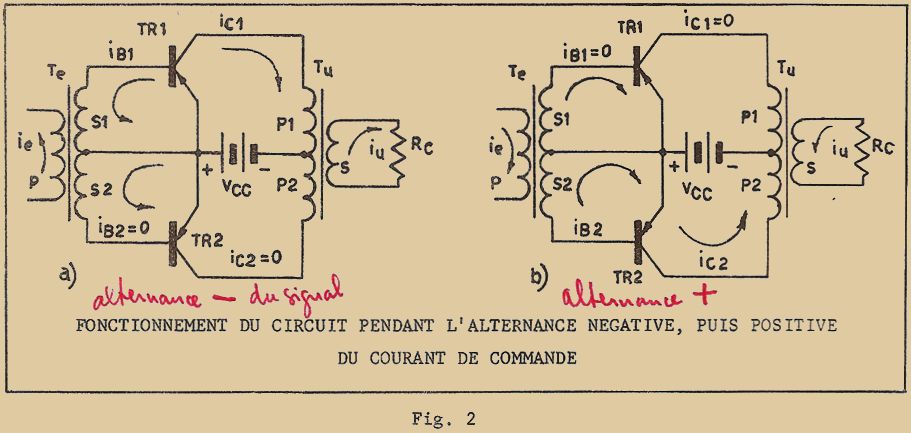
Si l’on considère maintenant l’alternance suivante, on trouve que le courant i_e a le sens opposé à celui de tout à l’heure (figure 2b). Les courants au secondaire s’inversent, et on démontre facilement que c’est maintenant le transistor TR₂ qui conduit, tandis que TR₁ se trouve bloqué.

Dans le primaire du transformateur T_u, va circuler le courant i_C2 avec le sens indiqué et le courant induit au secondaire aura donc le sens de la figure 2b.

En conclusion nous dirons, que pendant les alternances négatives, TR₁ conduit seul, et pendant les alternances positives, TR₂ seul.

Le transformateur d’entrée fait donc une "séparation" entre les 2 alternances : la première seule est amplifiée par TR₁, la seconde par TR₂.

Le transformateur de sortie fait l’opération inverse : il "recompose" les 2 alternances et délivre un signal complet à la charge d’utilisation.

Pour les alternances négatives de ie, tout se passe comme si le circuit était composé de S1, TR₁ et P1 ; pour les alternances positives, le circuit est composé de S2, TR₂ et P2 ; comme le secondaire de T_u est commun aux circuits des 2 collecteurs, le courant dans la charge est induit alternativement, une fois par i_C1 qui traverse P1, une fois par i_C2 qui traverse P2. On obtient ainsi la recombinaison du signal.

Comme la pile d’alimentation est commune aux circuits des 2 collecteurs, elle fournira le courant, alternativement à l’un puis à l’autre, et comme on peut le voir sur la figure 2, les courants i_C1 et i_C2 ont le même sens dans la pile. Il nous reste à vérifier que le circuit en classe B n’absorbe du courant que lorsqu’on lui applique un signal. Supposons que le courant i_e est sinusoïdal et que les alternances positives sont vers le bas, tandis que les alternances négatives vers le haut (ce n’est qu’une convention). Le courant i_e est représenté sur la figure 3a (2 périodes complètes). Les alternances négatives de i_e sont donc comprises dans les intervalles 1,2 et 3,4.

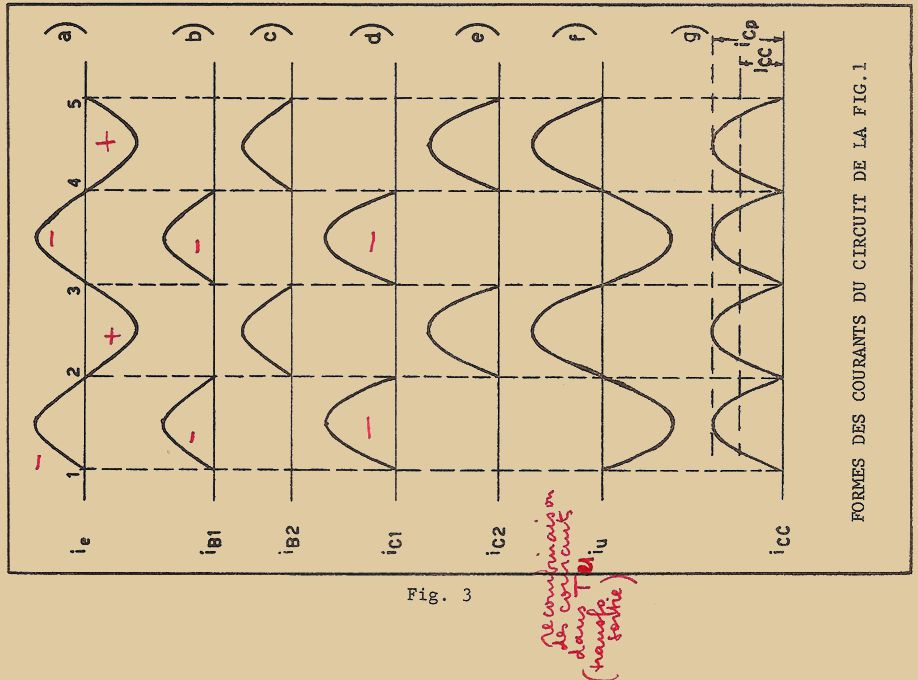
Le courant i_B1 n’existera donc que dans les intervalles 1,2 et 3,4 (figure 3b) ; le courant i_C1 , n’existera donc que dans les mêmes intervalles de temps, mais son amplitude sera beaucoup plus grande (figure 3d).

Dans les intervalles de temps 2,3 et 4,5, c’est-à-dire pour les alternances positives de i_e, nous aurons au contraire le courant i_B2 et i_C2 (figures 3c et 3e). Les 2 se recombinant dans le transformateur de sortie, donnent lieu au courant iu (figure 3f).

En nous rappelant que par convention nous avons admis que les alternances négatives étaient vers le haut, les courants de base et de collecteur sont donc vers le haut, puisqu’il s’agit de transistors PNP et qu’ils sont alimentés par des tensions négatives.

Le courant d’utilisation sera aussi alternativement positif et négatif comme le courant i_e.

A la figure 3g est reportée la forme du courant i_CC délivré par la pile : comme cette dernière alimente en même temps les 2 transistors, il est évident que l’allure du courant sera la résultante des courants des 2 collecteurs ; le courant i_CC sera constitué par une série d’alternances négatives de même forme et amplitude que les courants i_C1 et i_C2 .

La puissance fournie par la pile peut être déterminée facilement en faisant le produit de la tension V_CC de la pile par la valeur moyenne I_CC du courant i_CC de la figure 3g. En tenant compte que i_CC est constitué par des alternances toujours de même sens, dont l’amplitude est i_Cp, la valeur de I_CC est donnée par la formule suivante (valable uniquement dans le cas d’un signal sinusoïdal comme c’est le cas) :

I_CC = (2 x i_Cp)/π = i_Cp/1,57

La puissance fournie par la pile est donc :

P_CC = (V_CC x i_Cp)/1,57

et sera exprimée en milliwatts, si la tension est en volts et le courant en mA.

1 – 2 ÉTAGE DE SORTIE CLASSE B SANS TRANSFORMATEUR DE SORTIE

Dans le cas des amplificateurs push-pull, le rôle du transformateur de sortie est double. Il sert tout d’abord à transformer la faible valeur de l’impédance de la bobine mobile du H.P. en une impédance optimum pour que le transistor puisse délivrer la puissance maximum. D’autre part, il sert à recombiner les 2 alternances du signal.

Comme nous l’avons vu dans la précédente leçon, le transformateur introduit toujours des pertes, dûes principalement à la résistance des enroulements. Il est donc logique de chercher une solution pour l’éliminer et alimenter directement la bobine du haut-parleur.

Pour ce faire, on utilise des H.P. de type spécial, ayant une grande impédance de bobine mobile, de façon à pouvoir les brancher directement dans le circuit des collecteurs. En second lieu, il est indispensable que la bobine mobile soit pourvue d’une prise centrale pour obtenir la recombinaison des 2 alternances.

Avec un tel type de H.P., on obtient le schéma de la figure 4, identique à celui de la figure 1, avec la seule différence que c’est maintenant le H.P. qui est directement relié sur les collecteurs.

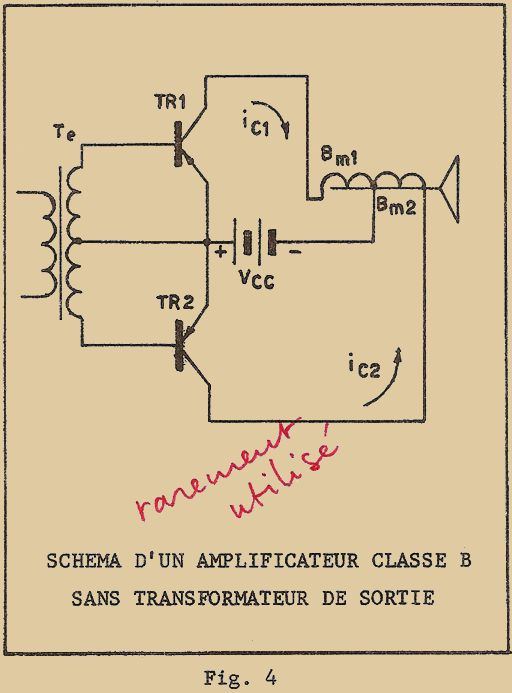
L’avantage de l’élimination du transformateur de sortie se traduit pour une même paire de transistors, par un gain de la puissance de sortie de l’ordre de 15%, ce qui signifie en d’autres termes, un meilleur rendement de l’étage. Par contre, on a l’inconvénient d’avoir un haut-parleur plus cher (nombre de spires plus grand pour avoir une impédance plus élevée, et prise centrale).

D’autre part, en regardant le schéma de la figure 4, on voit que le courant de TR₁ ne traverse seulement que la moitié gauche de la bobine mobile, et le courant de TR₂, la moitié droite. Comme les 2 transistors travaillent alternativement, chaque enroulement de la bobine travaille seulement la moitié du temps, ce qui indique une mauvaise utilisation de celle-ci.

La bobine mobile est donc 2 fois plus lourde qu’une bobine normale de même impédance (2 fois plus de spires) le H.P est donc moins sensible et moins capable de répondre aux variations rapides du courant B.F.

Ces inconvénients (mauvaise réponses aux fréquences basses et prix élevé) font que l’avantage que l’on avait obtenu par la suppression du transformateur de sortie est en grande partie perdu. Le schéma de la figure 4 est donc rarement utilisé.

Le schéma de la figure 5 est par contre beaucoup plus utilisé. Il permet en effet d’éliminer le transformateur de sortie et en même temps d’utiliser un H.P. à simple bobine mobile.

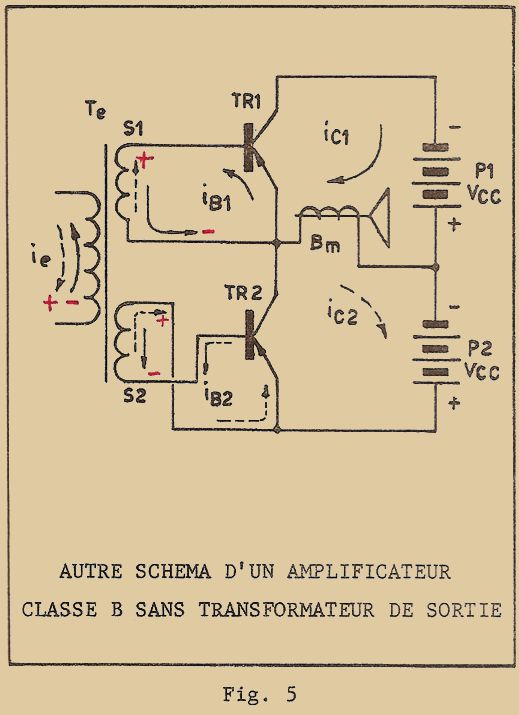
Dans ce cas on peut dire que les 2 transistors sont branchés en série, puisque le collecteur de TR₂ est relié directement à l’émetteur de TR₁. L’alimentation est réalisée par 2 piles identiques, branchées elles aussi en série et dont les extrémités sont reliées, l’une au collecteur de TR₁, l’autre à l’émetteur de TR₂. On peut utiliser aussi une pile unique qui comporte une prise centrale. Le H.P. dont la bobine mobile est à haute impédance (et plus précisément, d’impédance égale à la valeur de la résistance de charge requise pour le type de transistors utilisés), est relié entre le point de jonction de l’émetteur de TR₁ et du collecteur de TR₂ et le point de jonction des 2 piles.

La commande des bases est faite par 2 enroulements secondaires séparés au lieu que ce soit un seul enroulement secondaire à prise médiane. Le fonctionnement du circuit est le suivant :

Supposons que pendant l’alternance négative du signal d’entrée, le courant i_e dans le primaire ait le sens de la flèche en trait plein (figure 5). Le sens de la f-é-m (force électromotrice) dans les 2 secondaires sera celui indiqué par une flèche en trait continu (même sens que celui du courant).

On voit donc, que pour le transistor TR₁, le sens est celui de la flèche de l’émetteur, ce qui signifie que TR₁ conduit et que la bobine mobile est traversée par le courant i_C1 qui va de droite vers la gauche ; ce courant est fourni par la pile P1.

Le transistor TR₂ est par contre bloqué à cause du croisement des connexions du secondaire S2 entre base et émetteur de TR₂. La tension de commande a donc un sens inverse de celui de la flèche de l’émetteur ; aucun courant ne circule dans TR₂. La bobine mobile du H.P. est donc traversée par le seul courant i_C1 .

Pendant l’alternance positive, les courants primaires et tensions secondaires ont le sens indiqué par les flèches en pointillés (opposé au sens précédent). TR₂ conduit donc, tandis que TR₁ est bloqué. La bobine mobile est donc traversée par le courant i_C2 qui, grâce à la disposition du circuit, est fourni par la pile P2 et se dirige de la gauche vers la droite.

Dans ce cas encore, les 2 transistors travaillent alternativement pendant les alternances positives et négatives. Comme leur_s courants de collecteur traversent la bobine mobile en sens inverse, on obtient automatiquement la recombinaison des 2 alternances, sans avoir à utiliser un transformateur de sortie ou un H.P. à prise médiane.

À remarquer encore, que même maintenant, si on n’applique pas de signal à l’entrée, les 2 transistors restent bloqués et que dans ces conditions, la pile ne débite pas, tout comme précédemment.

Le circuit de la figure 5 a donc des avantages sensibles par rapport aux 2 autres. En effet, par rapport au schéma de la figure 1, il n’y a pas de transformateur de sortie : donc pour un même type de transistors, on obtient une puissance sensiblement plus grande, et une distorsion moindre, puisque en tous les cas, on n’a pas celles introduites par le transformateur de sortie. On a, en outre, une bande passante plus grande (on verra par la suite ce que cela signifie), toujours pour la même raison, qu’il n’y a pas de limitations dûes au transformateur. En conclusion, le circuit de la figure 5 est de plus grande fidélité que celui de la figure 1.

Par rapport au schéma de la figure 4, le circuit de la figure 5 a en outre l’avantage d’utiliser un H.P. moins coûteux et ayant des qualités électriques et acoustiques meilleures.

Par contre, les inconvénients du circuit de la figure 5 sont les suivants : l’alimentation doit être faite par 2 piles et le transformateur d’entrée doit avoir 2 enroulements secondaires séparés au lieu d’avoir une seule prise centrale. Ces inconvénients sont toutefois minimes, tant du point de vue électrique, que du point de vue économique.

1 – 3 ÉTAGE FINAL EN CLASSE B, SANS TRANSFORMATEUR D’ENTRÉE NI DE SORTIE

Outre l’élimination du transformateur de sortie, on peut encore supprimer à l’aide d’un montage approprié, le transformateur d’entrée, en rendant le circuit extrêmement simple et de grande qualité.

Pour pouvoir éliminer le transformateur d’entrée, il faut utiliser 2 transistors ayant mêmes caractéristiques, mais du type complémentaires, c’est-à-dire un de type PNP et l’autre du type NPN, en exploitant le fait qu’ils travaillent avec des tensions de polarité inverse.

Le schéma est indiqué à la figure 6 : le transistor TR₁ du type PNP est alimenté par la pile P1 dont la borne moins est reliée au collecteur du transistor ; le transistor TR₂ est du type NPN et est au contraire alimenté par la pile P2, dont la borne plus est reliée au collecteur de ce dernier. La bobine mobile B_m du H.P. est branchée entre le point A de jonction entre les émetteurs des 2 transistors et le point B de jonction des 2 piles ; elle est ainsi traversée par les courants de collecteur des 2 transistors.

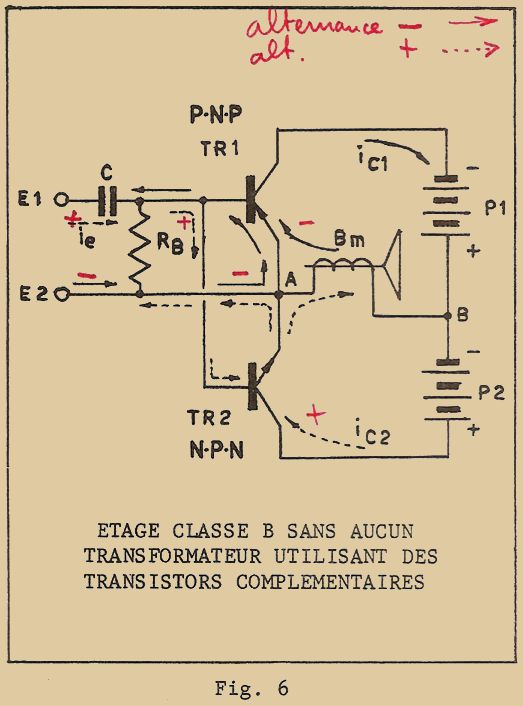
Le schéma est donc parfaitement analogue à celui de la figure 5, sauf en ce qui concerne l’inversion de branchement de TR₂ (collecteur permuté avec l’émetteur), car celui-ci étant du type NPN nécessite une tension positive sur son collecteur au lieu d’une tension négative.

Les 2 bases sont reliées ensemble puis aux émetteurs par l’intermédiaire de la résistance R_B ; ainsi, en l’absence du signal de commande, les 2 transistors se trouvent bloqués et aucun courant ne circule dans les collecteurs, tout comme dans les cas précédents.

Le signal de commande est appliqué, par l’intermédiaire du condensateur C, à l’ensemble des 2 bases ; comme les transistors sont complémentaires, l’un conduit pendant les alternances négatives, l’autre seulement pendant les alternances positives, sans nécessité de transformateur d’entrée, indispensable dans les schémas précédents.

Pendant l’alternance négative du signal de commande, le courant i_e circule de la borne E2 vers la borne E1 : ce courant a le sens indiqué par la flèche en trait continu (figure 6). Ce courant peut traverser la jonction émetteur-base de TR₁ car il a même sens que la flèche de l’émetteur de TR₁. Par contre il ne peut circuler dans la jonction émetteur-base de TR₂ car il a le sens opposé à celui de la flèche d’émetteur de ce transistor.

Ainsi, pendant les alternances négatives du signal, seul TR₁ conduira et la bobine mobile du H.P. sera parcourue par un courant i_C1 allant de la droite vers la gauche et fourni par la pile P1.

Pendant l’alternance positive, le courant i_e circule de la borne E1 vers la borne E2. Maintenant, c’est le transistor TR₁ qui est bloqué et TR₂ conduit (flèches en pointillés). La bobine mobile est traversée par le courant i_C2 allant de la gauche vers la droite et délivré par la pile P2.

Cette solution extrêmement élégante, est seulement d’un intérêt théorique, car la difficulté de réaliser en pratique 2 transistors de types complémentaires et de caractéristiques identiques est presque insurmontable. En effet, si les 2 transistors n’ont pas des caractéristiques parfaitement identiques, les courants des 2 collecteurs ne seront pas de même amplitude et le signal sera distordu.

Ce qui vient d’être dit reste valable en ce qui concerne les circuits où les 2 transistors sont du même type. Les transistors destinés à être montés dans des circuits push-pull sont en général apairés par le fabricant, de façon à réduire les inévitables différences (dûes aux tolérances de production) entre les caractéristiques des 2 transistors.

2 – EXEMPLE D’AMPLIFICATEUR EN CLASSE B

Comme nous l’avons fait dans la dernière leçon, lors de l’étude d’un amplificateur de puissance classe A, nous allons examiner maintenant le schéma d’un amplificateur classe B sur lequel nous ferons un exemple numérique. Pour simplifier, nous ne considérerons que l’amplificateur avec transformateur de sortie, car c’est celui qui est le plus largement diffusé dans la pratique. À partir de celui-ci, il sera facile de passer à n’importe quel autre type étudié dans cette leçon.

Le schéma en question est dessiné à la figure 7. Le schéma est identique à celui de la figure 1 à part les différences suivantes : le haut-parleur est remplacé par sa résistance équivalente RS, supposé être de 5Ω. On a mis en évidence dans le transformateur de sortie, la résistance de l’enroulement primaire (r_p = 2Ω pour chaque demi-primaire) et la résistance du secondaire (r_s = 0,6Ω) ; le primaire du transformateur d’entrée est alimenté par l’intermédiaire de la résistance R de valeur suffisamment élevée, par rapport à la résistance d’entrée de chacun des transistors, de façon que le circuit puisse être considéré comme étant commandé en courant (leçon théorique 15). Le réglage du courant de commande est fait à l’aide du potentiomètre P_e.

Pour l’instant, nous ne faisons aucune supposition sur la valeur du rapport de transformation des 2 transformateurs, et nous négligeons pour simplifier les résistances des enroulements de T_e.

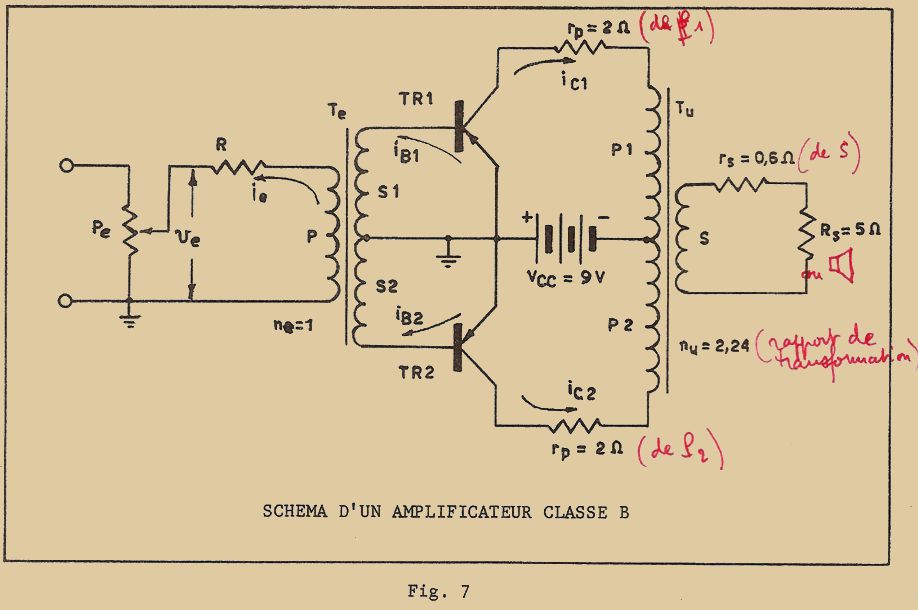
2 – 1 DROITE DE CHARGE

Étant donné que dans les étages push-pull classe B, les 2 transistors ne travaillent jamais simultanément, mais chacun à son tour nous pouvons faire l’étude complète de l’amplificateur en ne considérant qu’un seul transistor, celui qui conduit naturellement.

Il faut, avant tout, déterminer le point de repos A’ sur les caractéristiques, c’est-à-dire le point qui représente les conditions où se trouve le transistor lorsqu’aucun signal n’est appliqué à son entrée. Comme dans ces conditions, le courant de collecteur est nul (en effet, le transistor se trouve polarisé à l’interdiction), le point de repos se trouve sur l’axe horizontal de la caractéristique du 1^er quadrant de la figure 8. À noter que pour ce transistor, et en général pour tous les transistors de puissance, cet axe coïncide aussi avec la caractéristique relative à un courant de base nul (-I_B = 0).

Nous voyons donc que le point de repos se trouve en correspondance avec la valeur de la tension d’alimentation V_CC (point A’ de la figure 8) puisque le courant de collecteur I_Co est nul et qu’il n’y a donc aucune chute de tension dans le circuit des collecteurs, et que toute la tension de la pile se trouve appliquée entre le collecteur et l’émetteur du transistor. Nous avons donc V_CEo1 = V_CC = 9V.

Ainsi, lorsqu’il s’agit de déterminer le point de repos des transistors dans un étage classe B, il est inutile de tracer la droite de charge statique (qui dans le cas de l’exemple, aurait eu une pente correspondant à la valeur r_p = 2Ω), puisque dans les conditions de repos, le courant de collecteur est nul.

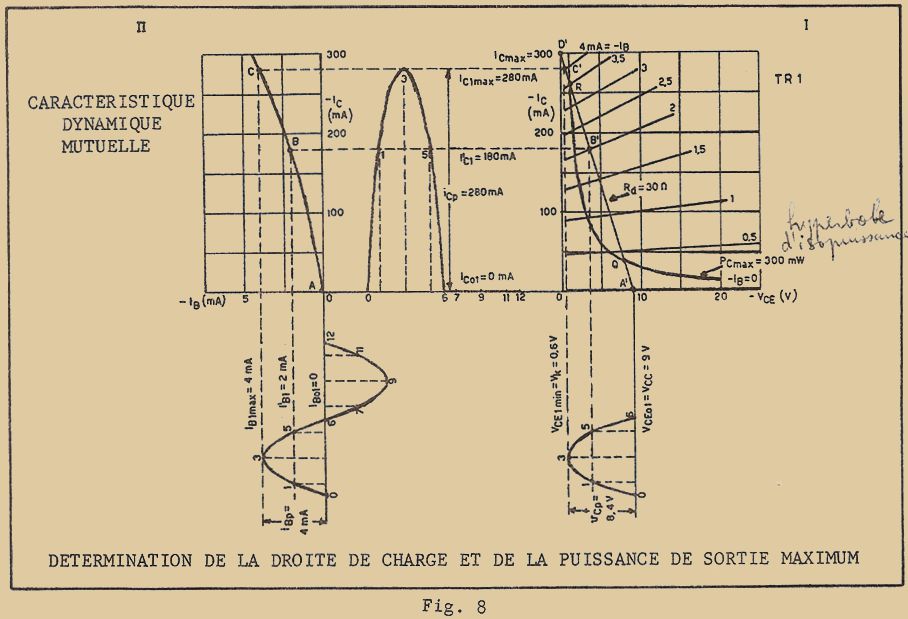
Après avoir déterminé le point de repos, nous pouvons maintenant tracer la droite de charge dynamique. Pour obtenir la puissance de sortie maximum, sans dépasser la valeur limite du courant collecteur I_Cmax (qui pour un type donné est par exemple de 300 mA), nous considérons sur l’axe vertical le point D’ correspondant à cette valeur maximum du courant, et nous tracerons la droite de charge qui passe par les points A’ et D’ (figure 8).

La résistance de charge dynamique aura donc pour valeur :

R_d = V_CC/I_Cmax = (9 V)/(300 mA) = 0,03kΩ = 30Ω

D’après le schéma de la figure 7, nous voyons que la résistance dynamique R_d se confond avec la résistance R_c présentée par la moitié de l’enroulement primaire du transformateur de sortie, car nous ne voyons aucune autre résistance, ni dans le circuit du collecteur, ni dans celui de l’émetteur.

En appliquant alors la formule donnée dans la leçon précédente, nous pouvons déterminer la valeur du rapport de transformation n_u de T_u, pour que R_d ait bien la valeur de 30Ω. Nous obtenons :

n_u = √((R_d - r_p)/(R_s + r_s )) = √((30-2)/(5+0,6)) = √(28/5,6) = √5 = 2,24

Ce qui signifie que le nombre de spires de la moitié de l’enroulement primaire doit être 2,24 fois le nombre de spires du secondaire.

La résistance de charge R_s ramenée au primaire aura donc pour valeur :

R_p = R_s x n_u² = 5 x (2,24)² = 5 x 5 = 25Ω

2 – 2 PUISSANCE ET RENDEMENT

En procédant comme à l’habitude avec la droite de charge dynamique on passe du 1^er quadrant au second, pour obtenir la caractéristique dynamique mutuelle et ainsi à la détermination des formes du courant et de la tension du collecteur, lorsque la base vient à être commandée par un courant sinusoïdal.

En examinant le 1^er quadrant de la figure 8, on voit que le point de fonctionnement, en se déplaçant sur la droite de charge dynamique, peut atteindre au maximum le point C’ correspondant à la tension minimum possible en pratique du collecteur, qui dans le cas de l’exemple est de 0,6 V (tension V_k définie dans la leçon précédente) et au courant maximum de 280mA. En pratique le point de fonctionnement n’atteint jamais le point D’ qui correspond à la valeur limite I_Cmax de 300mA ; c’est une garantie supplémentaire de sécurité par le transistor.

Par le point C’ passe la caractéristique ayant comme paramètre I_B = 4mA ce qui signifie que pour amener le point de fonctionnement en C’, le courant de commande devra atteindre la valeur crête de 4 mA.

Supposons donc, qu’en réglant correctement le potentiomètre P_e du schéma de la figure 7, nous faisions circuler dans le circuit de base de TR₁, un courant sinusoïdal de commande i_Bp = 4mA de valeur crête. La sinusoïde qui représente ce courant de base peut donc être dessinée comme d’habitude, en prenant comme axe, la verticale passant par le point de repos A du 2^ème quadrant. La construction graphique de la forme du courant et de la tension de collecteur sera faite en tenant compte de ce que pendant la 1ère alternance (0 à 6), le point de fonctionnement se déplace de A à C et revient en A : le courant de base passe donc de zéro, à la valeur maximum I_B1 max = 4mA pour revenir à zéro.

Pendant la seconde alternance (6 à 12), le courant de base ne peut pas descendre en dessous de zéro et le point de fonctionnement reste constamment en A.

Comme nous pouvons le voir d’après la figure 8, le courant de collecteur ne circule que pendant la pseudo période 0 – 6, et est égal à zéro, pendant toute la pseudo période 6 – 12. Nous avons tracé sur la même ligne, la forme de la tension de collecteur, mais seulement pendant la pseudo période où le transistor conduit. Nous verrons par la suite ce qu’il en advient de VCE pendant l’autre alternance.

A cause d’une légère courbure de la caractéristique dynamique mutuelle la forme du courant de collecteur est légèrement différente d’une sinusoïde. En effet, si nous regardons aux points 1 et 5, nous voyons que si le courant de base est bien égal à la moitié de la valeur crête (I'_B1 = 2 mA en effet), le courant de collecteur par contre a pour valeur I'_C1 = 180 mA, c’est-à-dire sensiblement plus grand que la moitié de la valeur maximum I_Cmax = 280 mA. Or nous savons que les formules permettant de calculer la puissance de sortie P_o1 du transistor, la puissance P_CC1 fournie par la pile, la puissance P_C1 dissipée dans le transistor et le rendement, ne sont valables que dans le cas d’un courant de collecteur parfaitement sinusoïdal.

Toutefois, comme la différence avec la forme sinusoïdale est encore assez faible, ces formules resteront valables avec une bonne approximation.

Nous supposerons encore que les courants des 2 transistors sont parfaitement égaux (ce qui suppose que les 2 transistors sont parfaitement identiques, chose qui en pratique n’est vraie qu’en première approximation). On a pris l’habitude, dans ces calculs, de ne considérer qu’un seul transistor, c’est-à-dire pendant une alternance seulement. Pour cette raison, les formules que nous avons vues précédemment ne sont plus valables. Les formules que je vais vous indiquer ci-dessous en découlent ; pour obtenir la puissance relative à l’étage complet, ces valeurs devront être multipliées par 2.

En supposant donc que le courant de collecteur est sinusoïdal, la puissance maximum que peut délivrer le transistor sera donc obtenue lorsque le point de fonctionnement atteint son excur_sion maximum, c’est-à-dire la valeur maximum de 280 mA. Cette puissance peut donc être calculée à l’aide de la formule suivante :

P_o1 = (i_Cp² x R_d)/4 avec :

i_Cp en A
R_d en ohm
P_o1 en watt

Dans le cas de notre exemple, nous avons :

i_Cp = IC1max = 28 mA = 0,28 A et R_d = 30Ω

P_o1max = ((0,28)² x 30)/4 = (0,0784 x 30)/4 = 2,352/4 = 0,588 W

La puissance de sortie maximum pour chacun des transistors du schéma de la figure 7 est donc de 588mW ; la puissance délivrée par les 2 transistors est donc :

P_omax = 2 x P_o1max = 2 x 0,588 = 1,176W

La puissance moyenne que chaque transistor absorbe sur la pile est 0,802W environ (voir calculs page 6)

La puissance moyenne absorbée par les deux transistors est :

P_CCmax = 2 x P_CC1max = 2 x 0,802 = 1,604W

Le rendement de chaque transistor (égal au rendement de l’ensemble) peut maintenant être calculé en faisant le rapport entre P_o1max et P_CC1max (ou entre P_omax et P_CCmax) :

η = P_omax/P_CCmax = 1,176/1,604 = 0,733 soit 73,3%

Dans la détermination de la droite de charge, nous avons tenu compte de la valeur maximum du courant de collecteur admise pour le type de transistor utilisé, et nous avons fait en sorte que jamais pendant le fonctionnement, cette valeur ne soit dépassée. Par contre, nous n’avons pas encore vérifié si la puissance dissipée dans le transistor ne dépassait la valeur limite supposée de 300 mW. Faisons maintenant cette vérification.

On a tracé sur les caractéristiques du 1^er quadrant de la figure 8, l’hyperbole d’isopuissance, c’est-à-dire celle qui correspond à la dissipation maximum admise de 300 mW. Or, nous voyons que la droite de charge dynamique passe au-dessus de cette hyperbole ; nous serions donc tentés de croire que ce transistor travaille dans des conditions dangereuses.

En examinant de plus près le fonctionnement du transistor, nous verrons que les choses ne sont pas tout à fait ainsi. En effet, le point de fonctionnement n’est pas continuellement dans la "zone interdite" c’est-à-dire dans la région comprise entre les points Q et R, mais il ne la traverse que pendant l’alternance où le transistor conduit, puis, pendant la seconde alternance, le point revient en A’ (I_C nul) et le transistor se "repose".

A cause de l’inertie thermique du transistor, sa jonction ne peut pas s’échauffer instantanément pendant l’alternance de conduction et se refroidir immédiatement pendant l’alternance de repos. La température va donc se maintenir à une valeur presque constante. L’échauffement de la jonction n’est donc pas dû à la puissance maximum dissipée, pendant l’alternance de conduction, mais à la puissance moyenne dissipée pendant une période.

Le calcul de la puissance moyenne P_C dissipée sur le collecteur est immédiat, si l’on se rappelle ce qui s’est dit dans la leçon précédente. En effet, si la pile fournit la puissance P_CC et qu’une partie P_o de celle-ci seulement constitue le signal de sortie, il est évident que la différence n’est autre que la puissance P_C dissipée sur les collecteurs des 2 transistors.

Pour le transistor TR₁ seul, on trouve que la puissance dissipée sur son collecteur, dans les conditions où le signal de sortie est maximum, sera :

P_C1 = P_CC1 – P_o1 = 802 – 588 = 214mW

Il faut encore remarquer que la valeur de P_C1 dépend de l’amplitude du signal de sortie et qu’elle n’atteint pas sa valeur maximum lorsque le courant de collecteur est lui-même maximum. Pour vérifier que la dissipation sur le collecteur ne dépasse en aucun cas la valeur autorisée de 300mW, il reste encore à calculer P_C1 non pas dans le cas où le signal de sortie est maximum, mais dans le cas où P_C1 atteint elle-même sa valeur maximum.

Dans ce but, le graphique de la figure 9 montre, comment varient les différentes puissances (P_CC1, P_o1, P_C1) et le rendement η du transistor, lorsque l’amplitude i_Cp du courant de collecteur augmente de 0 à la valeur maximum de 280 mA.

Nous voyons qu’en augmentant i_Cp, la puissance P_CC1 fournie par la pile au transistor croît régulièrement (on dit en langage mathématique qu’elle croît linéairement) ; que la puissance P_o1 fournie par TR₁ augmente d’abord lentement, puis de plus en plus vite (elle suit une loi "parabolique").

La puissance P_C1 dissipée sur le collecteur (donnée pour chaque valeur de i_Cp par la différence entre les valeurs de P_CC1 et P_o1) augmente d’abord puis diminue ; elle atteint sa valeur maximum pour un courant i_Cpo de 191mA.

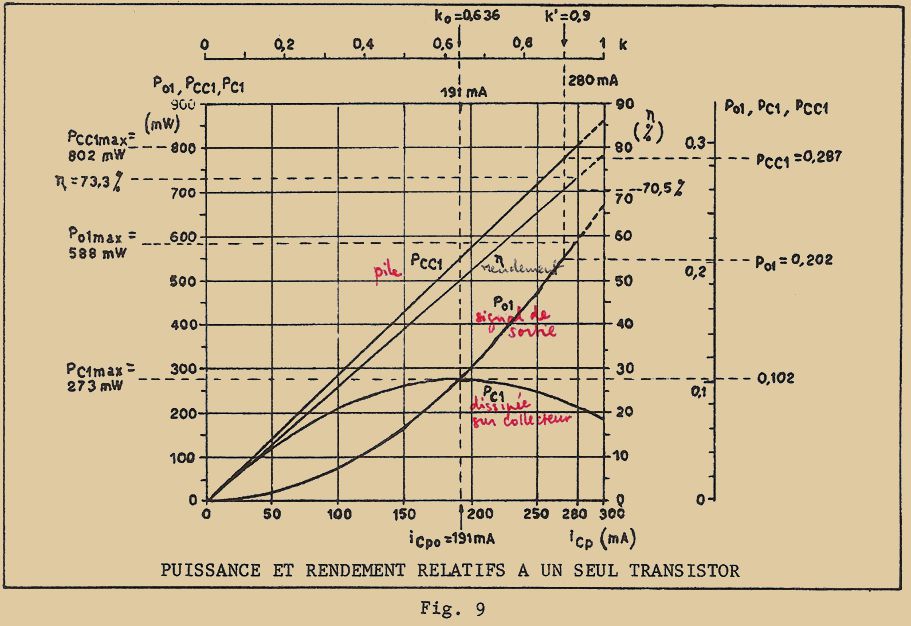
On démontre que cette valeur maximum est donnée par la formule :

P_C1max = (I_Cmax x V_CC)/π² = (I_Cmax x V_CC)/9,87

où V_CC est la tension de la pile exprimée en volts. P_C1max sera exprimée en watts ou en mW, selon que I_Cmax est donné en A ou en mA.

Dans le cas de l’exemple, on a : V_CC = 9V et I_Cmax = 300 mA

on a donc :

P_C1max = (300 x 9)/9,87 = 2.700/9,87 = 273mW

Cette valeur est donc plus faible que la valeur autorisée de 300mW et il n’existe donc pas de danger de destruction des transistors par échauffement. On démontre encore que la valeur i_Cpo pour laquelle P_C1 est maximum est donnée par la formule :

I_Cpo = 2/π x I_Cmax = 0,636 x I_Cmax = 0,636 x 300 = 191mA

A propos de la figure 9, il est bon encore de faire quelques remarques d’ordre général, valables non seulement pour le cas de l’exemple, mais aussi pour n’importe quel amplificateur de puissance de classe B.

En examinant la figure 9, nous voyons que lorsque l’amplitude du courant de collecteur est égale à la valeur i_Cpo (191mA dans l’exemple), non seulement la puissance P_C1 dissipée sur le collecteur atteint sa valeur maximum, mais elle est alors égale à la puissance P_o1 fournie par le transistor comme puissance du signal de sortie. On a donc :

P_C1 = P_o1

Par conséquent, et pour cette condition du fonctionnement, la puissance P_CC1 que le transistor absorbe sur la pile est égale à 2 fois la puissance P_o1 et le rendement η est alors de 50%.

Nous pouvons dire en d’autres termes, que la dissipation est maximum sur le collecteur, lorsque le rendement du transistor atteint 50%.

Le rendement du transistor augmente avec i_Cp et atteint la valeur maximum de 73,3% lorsque i_Cp = 280 mA suivant la construction de la figure 8. Pour cette valeur de i_Cp nous retrouvons évidemment sur le graphique de la figure 9, les valeurs P_CC1max = 802mW et P_o1max = 588mW calculées précédemment.

Il est intéressant de noter, que pour i_Cp = 300mA (c’est-à-dire si le point C’ de la figure 8, pouvait arriver en D’ correspondant au courant I_Cmax = V_CC/R_d ) le rendement est égal à la valeur théorique de 78,5%.

Le graphique de la figure 9 peut servir à calculer n’importe quel amplificateur classe B, par utilisation de l’échelle "réduite" de l’amplitude du courant de collecteur qui est :

k = i_Cp/I_Cmax.

L’échelle verticale porte les valeurs "réduites" des 3 puissances considérées correspondant à un seul des 2 transistors, c’est-à-dire la puissance "réduite" P_CC1 que le transistor absorbe sur la pile, la puissance "réduite" P_o1 délivrée par le transistor et la puissance (toujours "réduite") P_C1 dissipée sur le collecteur. Pour revenir aux puissances réelles, à partir des puissances "réduites", il suffit de multiplier ces dernières par un facteur "h" donné par le produit V_CC x I_Cmax. En exprimant la tension d’alimentation V_CC de la pile en volts, les puissances réelles seront données en mW ou en W, selon que I_Cmax (qui représente toujours le courant maximum de collecteur admis pour le type du transistor considéré) est exprimé en mA ou en A.

Les valeurs maxima des puissances "réduites" et du rendement, qui sont celles qui nous intéressent en pratique, sont lues en correspondance de la valeur k’ donnée par la formule :

k’ = (V_CC-V_k)/V_CC

où V_CC et V_k sont exprimées en volts. La puissance maximum "réduite" dissipée sur le collecteur se trouve toujours en correspondance de la valeur ko = 0,636.

Supposons par exemple que nous avons 2 transistors pour lesquels on admet un courant maximum de collecteur I_Cmax = 1,4A. La tension du coude V_k = 0,6V et la tension d’alimentation V_CC = 6V.

Avec ces données, nous trouvons :

h = V_CC x I_Cmax = 6 x 1,4 = 8,4W

k’= (V_CC-V_k)/V_CC = (6-0,6)/6 = 5,4/6 = 0,9

Sur le graphique de la figure 9, nous trouvons pour k’ = 0,9

P_o1 = 0,202  P_CC1 = 0,287  η = 70,5%

pour ko = 0,636, nous trouvons :

P_C1 = 0,102

Les valeurs réelles des puissances relatives à un seul des 2 transistors seront :

P_o1max = P_o1 x h = 0,202 x 8,4 = 1,7W

P_CC1max = P_CC1 x h = 0,287 x 8,4 = 2,41W

P_C1max = P_C1 x h = 0,102 x 8,4 = 0,85W

Les valeurs relatives à l’étage complet seront le double des valeurs précédentes.

2 – 3 PUISSANCE DE SORTIE ET RENDEMENT DE L’ÉTAGE

Comme pour les amplificateurs de puissance classe A, ceux en classe B ne peuvent délivrer à la charge (H.P. en général) toute la puissance Po fournie par les transistors à cause des pertes plus ou moins grandes mais inévitables dans le transformateur de sortie.

Si l’on considère un seul transistor ainsi que la moitié du primaire du transformateur de sortie qui lui correspond, la puissance que délivre le transistor au primaire est P_o1, tandis que la puissance P_u1 qui effectivement est appliquée à la charge, peut être déterminée de la même façon que pour un étage classe A.

P_u1 = P_o1 x R_p/R_d

Dans le cas de l’exemple nous avons P_o1max = 588mW. La résistance dynamique R_d = 30Ω ; la résistance secondaire ramenée au primaire R_p = 25Ω.

P_u1max = 588 x 25/30 = 588 x 0,833 = 490mW.

La puissance maximum fournie à la charge par les 2 transistors est donc le double.

P_max = 2 x P_u1max = 2 x 490 = 980mW = 0,98W

Nous pouvons encore calculer le rendement de l’étage, en faisant comme pour l’étage classe A, le rapport entre la puissance de sortie P_u et la puissance P_CC absorbée par les 2 transistors sur la pile.

Dans l’exemple nous avions P_CCmax = 1,604W

η = P_umax/P_CCmax = 0,98/1,604 = 0,6109 = 61,09%

Ce chiffre est sensiblement plus faible que le rendement η du transistor. Il nous reste encore, avant de terminer l’étude sur les étages finals push-pull classe B, à examiner les caractéristiques composites, les distorsions et les circuits de polarisation. Nous verrons ceci dans la prochaine leçon.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 19^ème LEÇON THÉORIQUE

1 – Le rendement d’un transistor est défini comme étant le rapport entre la puissance Po délivrée par celui-ci et la puissance PCo que ce dernier absorbe sur la pile d’alimentation.

2 – Les valeurs maxima théoriques du rendement d’un transistor sont 0,5 (soit 50%) et 0,785 (soit 78,5%) dans le cas d’un fonctionnement en classe A ou B respectivement.

3 - Les transistors d’un étage de sortie en classe A "chauffent" plus lorsque l’étage n’est pas excité ; par contre s’il s’agit d’un étage classe B, ils "chauffent" plus lorsque ce dernier travaille.

4 – La puissance maximum qu’un transistor en classe A peut fournir est égale à la moitié de la puissance maximum qu’il peut dissiper. S’il s’agit de 2 transistors en classe B au contraire, la puissance maximum qu’ils peuvent fournir est égale à 4,83 fois la puissance maximum que chacun d’eux peut dissiper.

5 – Le rendement d’un étage est toujours plus faible que celui des transistors, à cause des pertes qui se produisent dans le transformateur de sortie et dans la résistance de l’émetteur.

6 – Un transformateur réel peut être représenté par un transformateur idéal qui aurait en série avec chacun de ses enroulements, une résistance de valeur égale à la valeur de la résistance même de ses enroulements.

7 – Le schéma équivalent d’un transformateur réel, en ce qui concerne le courant continu, est constitué par une résistance dont la valeur est celle du primaire du transformateur.

8 – Pour éviter l’autodestruction d’un transistor de puissance, il faut que le coefficient de stabilité de son circuit de polarisation soit inférieur à une certaine valeur maximum tolérée.

9 – Pour réduire au minimum les distorsions d’un étage classe A à un seul transistor, il faut placer en série avec la base du transistor une résistance de valeur convenable.

---

EXERCICES DE RÉVISION SUR LA 20^ème LEÇON THÉORIQUE

1 – Combien doit-on utiliser de transistors dans un étage push-pull ? Comment doivent être ces transistors ?

2 – Pourquoi les 2 alternances d’un signal de sortie dans un étage push-pull sont-elles toujours parfaitement identiques ?

3 – Comment sont polarisés les transistors dans un étage classe B ?

4 – Quelle est la puissance absorbée sur la pile par l’étage classe B, lorsqu’aucun signal n’est appliqué à son entrée ?

5 – Lorsque l’on applique un signal à l’entrée, est-ce que les 2 transistors conduisent simultanément ?

6 – Est-ce que l’on peut supprimer le transformateur de sortie ?

7 – Pourquoi n’utilise-t-on pas en pratique, de transistors complémentaires ?

8 – Dans quelles conditions, la puissance dissipée sur le collecteur atteint-elle sa valeur maximum ?

9 - Pourquoi dans un étage classe B, la droite de charge tracée sur les caractéristiques de collecteur, peut-elle dépasser la courbe de dissipation maximum ?

Fin de la leçon 20

---

LECON 21

ETAGE PUSH-PULL - CARACTERISTIQUES COMPOSEES

Dans la leçon précédente, nous avons étudié l'étage de sortie push-pull classe B en considérant le comportement d'un seul transistor ; ceci était possible puisque les deux transistors conduisaient alternativement, l'un pendant  l'alternance négative, l'autre pendant l'alternance positive du signal de commande .

Pour étudier le comportement de l'étage d'un point de vue beaucoup plus complet, il faut considérer les deux transistors et "composer" leurs caractéristiques de façon à obtenir des courbes dites "composées" qui représentent non plus un seul transistor, mais l'ensemble des deux transistors.

Reprenons pour cela l'exemple de la figure 7 Théorie 20, où l'étage était piloté en courant et pour lequel les caractéristiques "composées" et les constructions graphiques qui s'y rapportent sont indiquées à la figure 1.

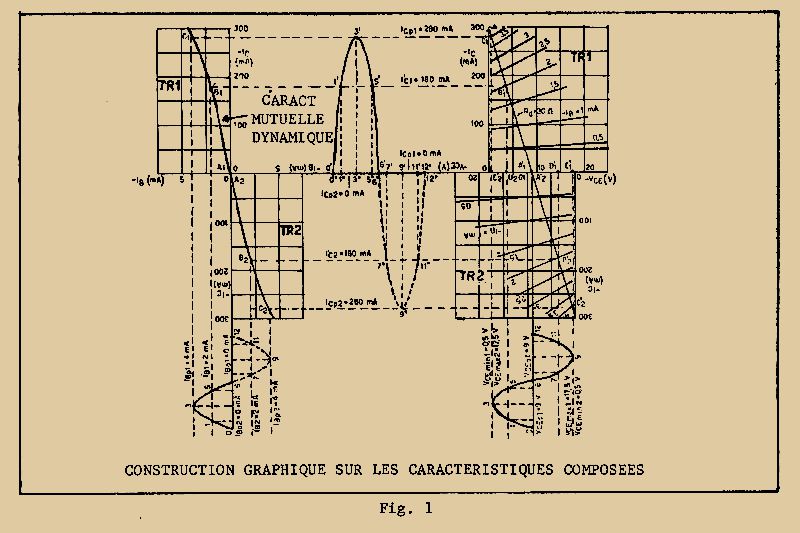
Comme il apparaît sur cette figure, les caractéristiques "composées" sont obtenues de façon très simple, en juxtaposant les caractéristiques du transistor TR₁ à celles de TR₂ après avoir retourné ces dernières par rapport aux premières et en les plaçant de telle sorte que les points de repos des deux transistors coïncident. Ainsi pour les caractéristiques de collecteur on fait coïncider le point de repos A'₁ (pour TR₁) avec A'₂ (pour TR₂). De cette manière, la droite de charge dynamique relative à TR₁, et celle relative à TR₂ se trouvent dans le prolongement l'une de l'autre et peuvent être considérées comme une droite de charge unique relative à un transistor fictif, formé par l'ensemble des deux transistors.

D'une façon analogue, nous obtenons la caractéristique dynamique mutuelle en composant les deux caractéristiques après avoir fait coïncider les points de repos A₁ et A₂.

Les constructions graphiques sont maintenant identiques à celles faites à la figure 8 de la Théorique 20. En traçant la sinusoïde de commande de la base avec une amplitude égale à 4mA et ayant comme axe de référence la verticale passant parle point de repos (A₁ = A₂) , nous voyons que pendant l'alternance 0-6, le point A₁ se déplace jusqu'en C1, puis revient à sa position de repos ; pendant l'alternance 6-12, le point A₂ se déplace jusqu'en C2, puis revient à sa position de départ.

En effectuant la construction, nous trouvons l'allure du courant de col-lecteur de TR₁ représentée par 0' -1' -3' -5' -6' -7' -9' -11' -12'. (en trait fin) et celle de TR₂ représentée par 0" -1" -3" -5" -6" -7" -9" -11" -12" (en pointillés). Etant donné que le transformateur de sortie recompose les deux alternances, la forme du courant délivré à la charge sera celle indiquée par 0' -1' -3' -5' -6' -7" -9" -11" -12"-, à part naturellement la valeur absolue du courant qui au secondaire du transformateur se trouvera multiplié par le rapport de transformation n.

Cette forme de courant peut être obtenue directement, sans avoir à considérer séparémment les deux transistors, en opérant directement sur les caractéristiques dynamiques mutuelles composées comme s'il s'agissait de la caractéristique d'un transistor fictif équivalent à l'ensemble des deux transistors et qui fonctionnerait en classe A. Le point de repos tombe alors au point milieu de la droite, c'est-à-dire en A₁ = A₂ et pendant le fonctionnement le point balaie la droite de C1 à C2.

On se rend compte tout de suite que la caractéristique "composée" est parfaitement symétrique par rapport au point de repos et que les deux alternances de sortie sont nécessairement identiques, ce que l'on avait difficilement dans un amplificateur classe A.

En passant par l'intermédiaire de la droite de charge, on détermine la forme de la tension de collecteur des deux transistors, forme qui est encore celle de la tension aux bornes de la charge, à part la valeur absolue de la tension. La tension au secondaire du transformateur de sortie est en effet n fois plus petite que celle au primaire.

Il faut encore remarquer que lorsqu'un transistor se trouve au cut-off, (par exemple TR₁ pendant l'alternance 6-12) la tension du collecteur ne reste pas constante et de valeur égale à celle de l'alimentation (soit 9 V dans le cas de l'exemple), mais dépasse cette valeur à cause de la tension induite dans la moitié du primaire P1 (figure 2b - Théorique 20) par le courant de collecteur de TR₂ qui parcourt l'autre moitié du primaire P2. L'inverse se produit pour la tension de TR₂ pendant l'alternance 0-6.

La valeur atteinte par la tension du collecteur pendant l'alternance où le transistor se trouve au cut-off peut être déterminée sur les caractéristiques de collecteur. Il suffit en effet de considérer la droite de charge "composée" et de déterminer sur celle-ci le point de fonctionnement à l'instant considéré.

Les tensions sur les deux collecteurs à cet instant, pourront être lues en correspondance du point de fonctionnement sur l'échelle horizontale relative à l'un ou l'autre transistor. Si l'on considère par exemple le point 9 du courant de commande, le point de fonctionnement sur la droite de charge "composée" se trouve en C'2 ; en correspondance de ce point, on lit sur l'échelle horizon-tale relative à TR₂, la valeur 0,5 V et sur celle relative à TR₁, on lit 17,5 V.

Ceci signifie que lorsque la tension de collecteur de TR₂ atteint la valeur minimum de 0,5 V, la tension de collecteur de TR₁ dépasse la valeur de la tension d'alimentation et atteint un maximum de 17,5 V. La forme de la tension de collecteur est tracée à la figure 1, et elle est valable pour les deux transistors : il suffira de lire les valeurs correspondantes des tensions sur les échelles relatives à l'un ou à l'autre.

Si on veut au contraire considérer séparemment le fonctionnement des deux transistors, on voit que pendant l'alternance de conduction 0-6, le point de fonctionnement de TR₁ se déplace, comme nous l'avons déjà vu sur la droite de charge de A'₁ à C'1 puis revient en A'₁.

Pendant l'alternance de blocage 6-12, il se déplace sur l'axe horizontal de A'₁ à E'1 puis revient en A'₁.

Le déplacement du point de fonctionnement sur l'axe horizontal de A'₁ à E'1 signifie en fait, que la tension du collecteur varie de 9 V à 17,5 V pendant que le courant reste nul puisque le transistor est au cut-off. On raisonnera de même pour la tension de collecteur de TR₂. Il faut donc se rappeler que pour un étage push-pull classe B comme d'ailleurs pour un simple étage en classe A, c'est-à-dire un étage quelconque couplé à la charge (ou à l'étage suivant) par l'intermédiaire d'un transformateur, la tension de collecteur peut dépasser largement la tension d'alimentation et atteindre des valeurs presque égales ou double de celle-ci.

Dans l'exemple, la tension atteinte est 17,5 V, donc presque le double de la tension d'alimentation (9 V). La tension de collecteur ne dépasse pas la valeur maximum de 20 V admise pour le transistor SFT 131.

DISTORSIONS ET CIRCUITS DE POLARISATION

En observant la forme du courant de collecteur de la figure 1, on remarquera, comme il a été déjà dit dans la leçon Théorique 20, que celui-ci n'est pas parfaitement sinusoïdal parce que le courant relatif aux points 1', 5', 7" et 11" n'est pas égal à la moitié du courant maximum comme cela devrait être. Il y a donc une distorsion introduite par la caractéristique dynamique mutuelle, qui n'est pas parfaitement rectiligne.

Cette distorsion cependant est relativement faible et peut être acceptée dans la plupart des cas. Il faut aussi remarquer qu'en général un étage de sortie n'est jamais commandé en courant, mais plutôt en tension.

En d'autres termes, dans un étage de sortie, on s'impose la forme de la tension appliquée au primaire du transformateur d'entrée, plutôt que la forme du courant qui traverse ce primaire, comme on l'a supposé dans le cas de l'exemple de la figure 1. Il est donc intéressant d'étudier le comportement du circuit commandé en tension, en particulier du point de vue des distorsions.

Pour que l'étage de sortie soit commandé en tension, au lieu de l'être en courant, le schéma de la figure 7 Théorique 20 doit être modifié comme il est indiqué à la figure 2, en utilisant un potentiomètre Pe de faible valeur et en supprimant la résistance R de forte valeur placée en série avec le primaire du transformateur d'entrée.

Les constructions relatives sont indiquées à la figure 3, où pour plus de clarté, on a négligé la construction relative à la tension du collecteur, qui comme on l'a vu à plusieurs reprises, est de forme identique à celle du cou-rant de collecteur.

Il faut tout d'abord, "composer" les caractéristiques d'entrée des deux transistors en faisant coïncider les points de repos A'₁ et A'₂ correspondant à un courant de base de zéro milliampère, et à une tension V_be nulle. La base se trouve donc au même potentiel que l'émetteur, c'est-à-dire à la masse, puisqu'elle est reliée à celle-ci par l'intermédiaire d'une moitié de l'enroulement secondaire du transformateur d'entrée.

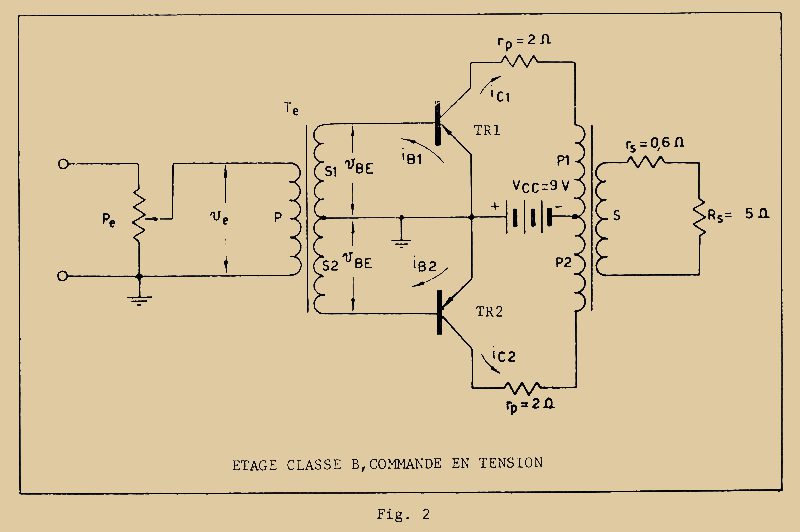
Si l'on désire que le courant de collecteur atteigne la valeur maximum de 280mA comme dans le cas précédent, le point de fonctionnement devra atteindre les points C'₁ et C'₂ sur la caractéristique d'entrée. D'après cette dernière, on voit que pour obtenir un courant de base de 4mA (correspondant à 280mA de courant de collecteur), la tension entre la base et l'émetteur devra avoir une valeur crête de 0,44 V (figure 3).

En effectuant les constructions graphiques, on trouve que le courant de commande de la base et par voie de conséquence le courant de collecteur est loin d'être sinusoïdal et en particulier aux intersections de la courbe avec l'axe de référence, c'est-à-dire aux points 0, 6 et 12.

Le courant de base (et le courant de collecteur) est nul pendant une fraction du temps assez grande autour de ces points.

La distorsion du courant de collecteur est très grande : il suffit d'observer que lorsque la tension de commande aux points 1, 5, 7 et 11 a une valeur égale à la moitié du maximum (V'_be = 0,22 V) le courant de collecteur est égal à 26mA seulement, c'est-à-dire à peine un dizième de la valeur maximum, au lieu d'être égal à la moitié.

Si l'on part avec une tension de commande d'amplitude plus faible (par exemple la moitié de celle de tout à l'heure), on voit que la distorsion est encore plus marquée et le courant du collecteur se réduit à des alternances assez séparées l'une de l'autre ; la valeur maximum du courant n'est pas réduite de moitié, mais de beaucoup plus (figure 3).

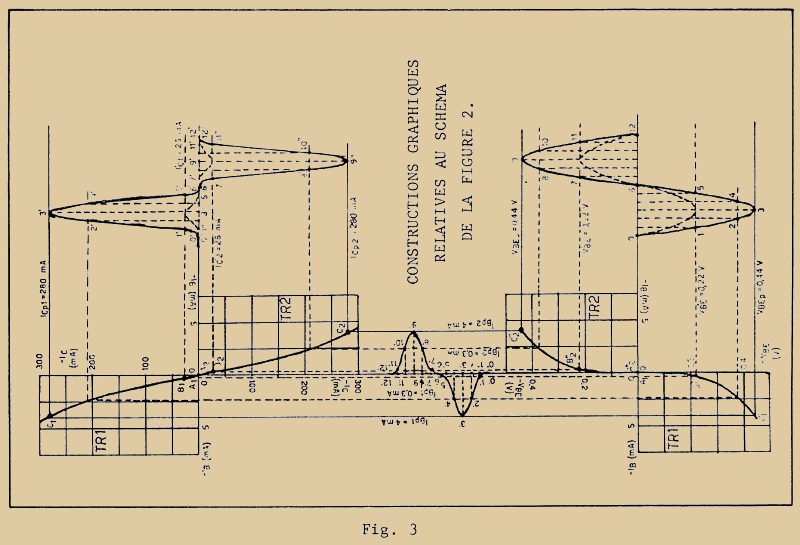
Si l'on examine la caractéristique d'entrée, on voit que le courant de base ne commence à circuler que lorsque la tension V_be est supérieure à 0,1V ; au-dessus de cette valeur, le courant de base croît, mais pas proportionnellement à la tension de commande; il croît d'abord très lentement, puis de plus en plus rapidement. Ce phénomène est visible sur la caractéristique d'entrée, qui jusqu'à des valeurs de tension de 0,1V environ, coïncide avec l'axe vertical, puis s'en éloigne mais d'une façon curviligne.

La distorsion du courant de base et du courant de collecteur est due à la courbure de la caractéristique d'entrée. C'est pour cette raison qu'on l'appelle "distorsion initiale". Pour éviter cet inconvénient, il faut polariser les bases des deux transistors de façon à ce qu'ils conduisent un peu en l'absence de signal.

Ceci peut être obtenu en reliant la prise milieu du secondaire du transformateur non pas à la masse, mais à un pont de résistances R₂ et R₃ qui donne une tension de quelques dizièmes de volt, comme indiqué sur la figure 4.

Supposons que la tension de polarisation ainsi obtenue soit de 0,2V, les points de repos A'₁et A'₂ se déplacent sur la caractéristique en correspondance de V_beo = 0,2V. Les deux caractéristiques d'entrée sont alors "composées" en faisant coïncider sur la même ligne horizontale ces points de repos (voir figure 5).

 

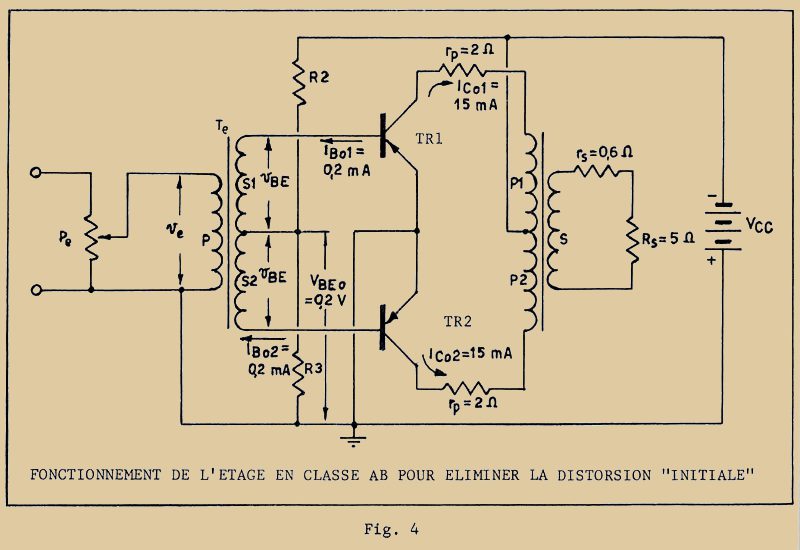
La construction graphique pour la détermination de la forme du courant de collecteur sera obtenue en dessinant tout d'abord la sinusoïde qui représente la tension de commande et axée sur 1' horizontale passant par les points de repos A'₁ et A'₂. Si l'on veut encore obtenir un courant maximum de collecteur de 280mA, correspondant à un courant de base de 4mA, le point de fonctionnement de chacun des transistors devra encore atteindre les points C' (C'₁ pour TR₁ et C'₂ pour TR₂) qui correspondent à une tension V_be de 0,44V, comme on l'a déjà vu à la figure 3. Mais comme maintenant en l'absence du signal de commande, les bases se trouvent déjà polarisées à 0,2V, pour les amener à 0,44V il suffira de leur appliquer une tension de commande d'amplitude maximum de: 0,44-0,2=0,24V (voir figure 5). En résumé, on applique sur les bases une tension de polarisation de 0,2V (c'est la composante continue) et une tension de commande de 0,24V crête (c'est la composante alternative).

On peut maintenant déterminer les formes des courants de base et de collecteur.

Lorsque la tension de commande est nulle (points 0-6 et 12) le courant de base n'est pas nul comme auparavant, mais a une valeur I_bo de 0,2mA ; le courant de collecteur Ico est de l'ordre de 15mA (figure 5).

Les deux transistors conduisent simultanément, même en l'absence de signal. Pendant l'alternance 0-6 de la tension de commande, le point de fonctionnement de TR₁ par exemple, se déplace de A'₁ jusqu'en C'₁ puis revient en A'₁ ; pendant l'alternance 6-12, le point de fonctionnement se déplace de A'₁ jusqu'en K'₁ puis revient en A'₁ le courant de base s'annule seulement lorsque le point de fonctionnement arrive en H'₁ correspondant aux points 7 et 11.

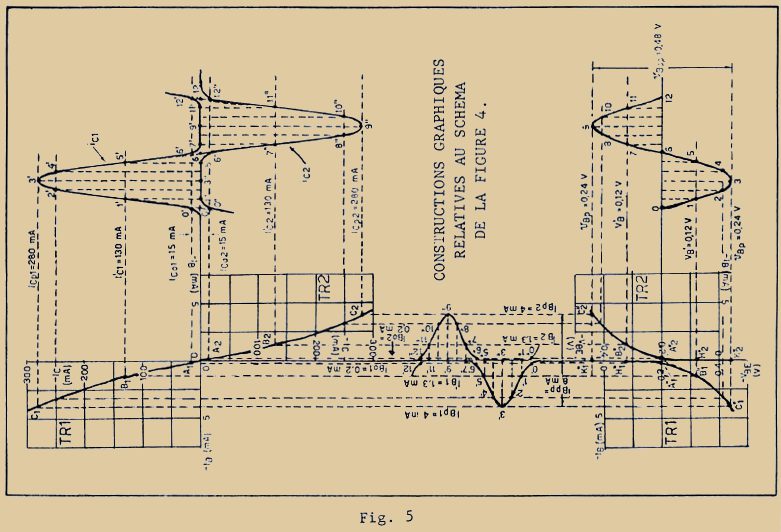
On en déduit que TR₁ conduit un peu plus d'une demi-période, puisqu'il conduit non seulement entre 0 et 6 mais encore jusqu'au point 7, puis recommence à conduire à partir du point 11, au lieu du point 12 comme avant. (On raisonnera de même pour TR₂).

En conclusion, nous dirons qu'avec cette polarisation appliquée aux deux transistors, ceux-ci conduisent pendant plus d'une demi-période du signal de commande, et qu'il existe en outre un intervalle de la période (intervalle 5 à 7) où les deux transistors conduisent simultanément. Un tel fonctionnement est intermédiaire entre celui de la classe B (où les deux transistors ne conduisaient que pendant une demi-période) et celui de la classe A (où ils conduisaient en permanence). Pour cette raison, on dit que l'étage travaille en classe AB.

Le courant dans la charge est obtenu en combinant les deux courants de collecteur ; il faut encore remarquer que I_c1 et I_c2 circulent dans les deux moitiés du primaire du transformateur de sortie en sens opposé et se compensent donc totalement ou en partie lorsqu'ils circulent simultanément.

Lorsqu'ils sont égaux (points 6' et 6" par exemple) ils se compensent parfaitement, et tout se passe comme s'il n'y avait pas de courant dans le primaire. Quand ils ne sont plus égaux, tout se passe comme si le primaire était traversé par leur différence.

On obtiendra donc la forme du courant résultant en faisant pour chaque point la différence entre les deux courants. Dans le cas de la figure 5, pendant l'intervalle de temps 1 - 5 - TR₁ conduit seul. Pendant l'intervalle 7 - 11, TR₂ conduit seul. La forme du courant est donc celle due aux transistors seuls, c'est-à-dire respectivement 1', 2', 3', 4', 5' et 7", 8", 9", 10", 11".

Dans l'intervalle de temps 5-7 les deux transistors conduisent simultanément et le courant résultant est dessiné en pointillés sur la figure, soit 5', 6 et 7".

La forme résultante pour une période est représentée par les points 0, 1', 2', 3', 4', 5', 6, 7", 8", 9", 10", 11", 12 , et est pratiquement sinusoïdale comme celle de la tension de commande.

On remarquera de même que le courant correspondant aux points l', 5', 7" et 11", est de 130mA, c'est-à-dire presque égal à la moitié de la valeur maximum. Les distorsions sont très réduites par rapport au cas de la figure 1.

On peut encore noter que la forme résultante du courant de collecteur peut être obtenue en considérant la caractéristique "composée" d'entrée obtenue à partir des deux caractéristiques, en faisant pour chaque valeur de la tension de commande, la différence entre les courants de base des deux transistors. Celle-ci coïncide avec celle des deux transistors seuls dans les régions C'₁ -B'₁ et B'₂ - C'₂ et celle dessinée en pointillés dans la région B'₁ - B'₁.

En considérant alors le point de fonctionnement qui se déplace sur une telle caractéristique de C'₁ à C'₂ pendant une période complète de la tension de commande, on détermine directement la forme des courants des bases et des collecteurs.

STABILISATION THERMIQUE

Comme tout autre circuit, l'étage push-pull classe B ou AB nécessite une compensation thermique de façon à éviter les inconvénients décrits dans la 19^ème leçon Théorique, à propos de la sécurité de fonctionnement des transis-tors de puissance.

La stabilisation thermique peut être obtenue à l'aide de l'une des méthodes indiquées en leur temps, et parmi lesquelles la plus simple consiste à insérer une résistance dans le circuit de l'émetteur. Dans le cas d'un étage push-pull, il y a deux possibilités : placer une résistance dans chacun des émetteurs, ou bien réunir les deux émetteurs ensemble et insérer une résistance commune. Cette dernière solution est la plus adaptée car plus économique (une seule résistance utilisée) et parce qu'elle présente quelques avantages du point de vue fonction-nement de l'étage (comme on pourrait le démontrer) .

Le schéma d'un étage push-pull classe AB avec stabilisation thermique est représentée à la figure 6 où la stabilisation est obtenue avec la résistance R_e placée dans les émetteurs et où le  pont R₂ - R₃ sert à la polarisation des deux transistors.

Pour obtenir une bonne stabilisation, il faut que R_e ait une valeur telle, qu'en l'absence de signal (au repos), la tension à ses bornes soit de l'ordre de un à deux dixièmes de la valeur de la tension d'alimentation.

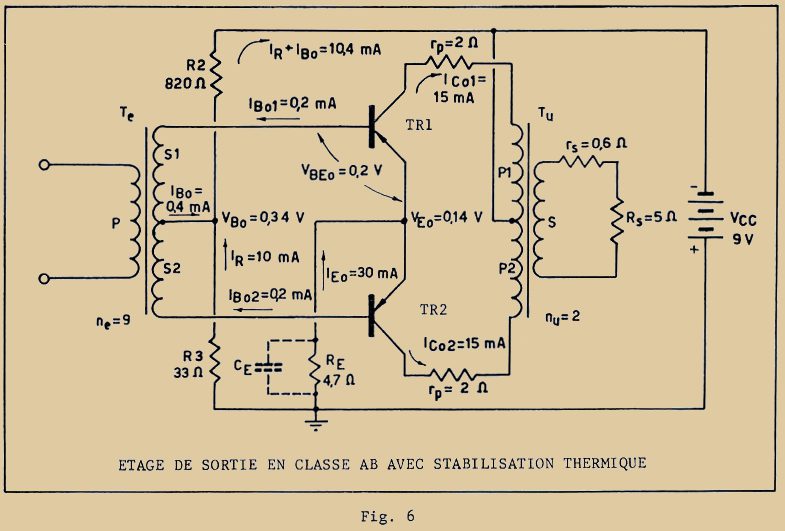
Dans l'exemple, on a Vcc = 9V, la chute de tension aux bornes de R_e doit être comprise entre 0,9 et 1,8V.

Comme R_e est parcourue par les deux courants de repos (chacun égal à 15mA), le courant I_eo total qui traverse R_e est donc de 30mA.

Si R = 4,7Ώ ft on a :

Veo = I_eo x R_e = 30mA x4,7Ώ = 141 mV =0,14V environ.

Cette valeur de la tension est acceptable et R_g convient donc.

On peut maintenant déterminer R₂ et R₃. Si l'on veut qu'au repos la tension V_beo, soit de 0,2V, on en déduit que la tension V_bo des deux bases doit être :

V_bo = V_eo + V_beo = 0,14 + 0,2 = 0,34V

En admettant un courant Ir dans le pont de 10mA et en considérant que R₂ est traversée par I_r et I_bo, (I_bo est égal à la somme des deux courants de base, soit à 0,4mA, puisque I_bo1 = I_b02 = 0,2mA).

Le calcul de R₂ et de R₃ donne :

R₃ = V_bo / I_r = 0,34V / 10mA = 0,034kΏ

En pratique on prendra des valeurs de résistances dans la série normalisée les plus proches, soit R₂ = 820Ώ et R₃ = 33Ώ (figure 6).

Le coefficient de stabilité S sera déterminé à l'aide de la formule connue ; R_b est égale à la mise en parallèle de R₂ et de R₃, soit R_b = 32Ώ environ. En supposant que ß = 100, on obtient :

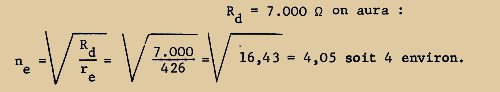
Cette valeur est acceptable, si l'on considère que pour les étages classe B et AB, la valeur maximum de S à ne pas dépasser, est donnée par la formule :

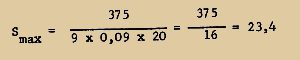
ici, on a :

V_cc = 9V ; K = 0,09°C/mW et I_cbo = 20µA

 

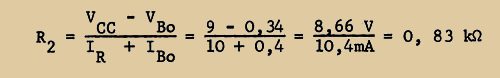
PUISSANCE DE SORTIE ET RENDEMENT

Bien que l'étage fonctionne dans les mêmes conditions que précédemment, la puissance délivrée à la charge est réduite à cause de la présence de la résistance R_e. En examinant en effet le schéma de la figure 6, on voit que la résistance R_e se trouve en série avec la liaison de l'émetteur c'est-à-dire qu'elle est traversée par le courant d'un transistor pendant une alternance du signal et par le courant de l'autre transistor pendant l'autre alternance,ce qui indique que R_e fait partie de la résistance dynamique R_d.

Comme la valeur de R_d doit rester celle qui a été calculée dans la précédente leçon, soit 30Ώ (puisque la résistance de charge R_s est restée inchangée et égale à 5Ώ) et en admettant que la résistance des enroulements reste la nême (r_p = 2Ώ et r_s = 0,6Ώ), le rapport de transformation n du transformateur ie sortie doit être modifié.

Pour avoir encore R_d = 30Ώ, le rapport n devra être :

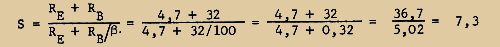
valeur arrondie à 2 en pratique.

La résistance de charge R_s ramenée au primaire est donc :

R_p = n² x R_s = (2)² x 5 = 4 x 5 = 20

La puissance maximum délivrée à la charge par un seul transistor sera donc : (P_o1max  = 588 mW puisque R_d est restée la même).

P_u1max = P_o1max = R_p / R_d = 588 x 20/30 = 588 x 0,666 = 392 mW

La puissance maximum fournie par les deux transistors est donc :

P_umax = 2 x 392 = 794mW au lieu de 980 mW comme précédemment.

Le rendement est donc réduit. La puissance absorbée par l'étage lorsque celui-ci délivre la puissance de sortie maximum, reste encore égale à 1,604W, le rendement est donc :

au lieu de 61,15% dans le cas précédent.

La présence de R_e amène donc une réduction de la puissance de sortie en ce  sens qu'elle est traversée par le courant qui constitue le signal de sortie des  transistors. On pourrait penser qu'il est possible d'éviter cette perte en mettant en parallèle sur R_e, un condensateur de valeur appropriée, comme on l'avait vu dans les 18ème et 19ème leçons Théoriques.

Mais il faut remarquer que dans le cas d'un amplificateur en classe B ou AB (comme toutes les fois où l'amplificateur n'est pas en classe A) il n'est pas possible de placer un condensateur en parallèle sur la résistance de l'émetteur pour la raison suivante.

Les courants des deux transistors traversent R_e dans la même direction c'est-à-dire que les alternances de la tension qui apparaît aux bornes de cette résistance suivent l'allure des alternances du courant de chacun des transistors. La formule du signal de sortie (tension ou courant) est représentée sur la même figure.

Si maintenant on place un condensateur Ce de capacité convenable en parallèle sur R_e (en pointillés sur la figure 6) ce condensateur va tendre à niveler la tension aux bornes de R_e en la rendant d'amplitude constante (figure 7b). La valeur V_em de la tension d'émetteur sera alors égale à la valeur moyenne de la tension développée aux bornes de R_e que l'on avait en l'absence de Ce (ligne en pointillés sur la figure 7a).

Les deux émetteurs se trouvant alors polarisés à la tension V_em qui est négative dans le cas des transistors PNP puisque le courant I d'émetteur traverse R_e dans la direction masse-émetteur, ce qui indique que les transistors ne vont conduire que lorsque la tension appliquée à leurs bases (signal d'entrée) dépassera la valeur V_em.

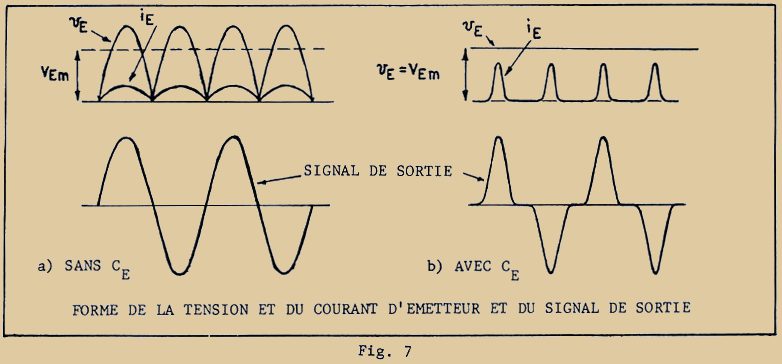
Le phénomène est analogue à celui indiqué à la figure 3. Les transistors ne conduisent plus pendant toute la durée d'une demi-période (figure 7b) et le courant et la tension de sortie sont distordues 'exactement comme dans le cas de la figure 3).

Il y a cependant une différence fondamentale dans les deux types de distorsion.

Dans le cas de la figure 3, la distorsion était plus évidente pour les signaux de faible amplitude que pour ceux de grande amplitude. Dans le cas de la figure 7 au contraire, la distorsion reste toujours la même que le signal soit de faible ou de grande amplitude, car la tension V augmente lorsque l'amplitude du signal d'entrée croît.

Pour cette raison, il n'est donc pas possible d'utiliser un condensateur Ce dans les étages classe B ou AB. On doit donc accepter la réduction de la puissance de sortie provoquée par R_e ; la valeur de cette résistance d'ailleurs doit rester la plus faible possible et compatible avec la stabilité thermique requise.

RESISTANCE D'ENTREE

On peut définir aussi la valeur de la résistance d'entrée du transistor et de l'étage push-pull classe B ou AB, nécessaire pour déterminer le rapport de transformation du transformateur d'entrée.

La résistance d'entrée r_g des transistors est définie de la même manière que celle relative à un étage à un seul transistor classe A (revoir Théorique 19) et comme étant le rapport entre l'excursion V_bpp de la composante alternative de la tension de base et l'excursion I_bpp de la composante alternative du courant de base.

En regardant la figure 5, on trouve :

R_b = V_bpp/I_bpp = 0,48V/8mA = 0,06kΏ = 60Ώ

Cette valeur de la résistance est celle que présente alternativement chaque transistor pendant la demi-période où il conduit.

Pour déterminer la valeur de la résistance d'entrée de l'étage il faut faire quelques remarques. Avant toute chose, il faut dire que la résistance R_e est définie comme étant le rapport entre la tension Ve délivrée par un demi-enroule-ment du secondaire du transformateur d'entrée et le courant Ib qui traverse le circuit de base d'un des transistors.

En supposant que l'on ne considère que la seule alternance pendant laquelle TR₁ conduit, on fera le calcul au moment où I_b1, atteint sa valeur maximum : I_b1  = 4mA, comme il résulte de la construction de la figure 5. Dans ces conditions, la valeur V_b de la tension de base atteint son maximum : V_bp  = 0,24V.

En reprenant l'examen du schéma de l'étage (redessiné à la figure 8), on notera que le courant de commande de la base de TR₁ circule suivant les flèches de la figure : jonction base - émetteur de TR₁, secondaire S1 du transformateur d'entrée, résistance R₃, résistance R_e.

Le secondaire S1 devra donc délivrer une tension dont la valeur maximum V_ep est plus grande que V_bp1, puisqu'elle doit compenser la chute de tension aux bornes de R₃ et de R_e. Elle devra être :

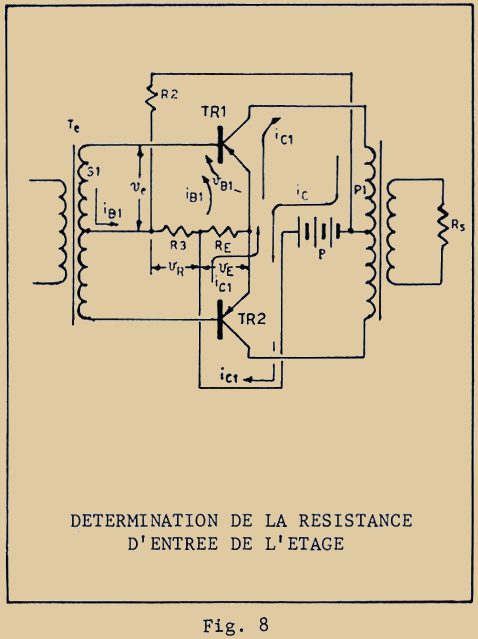
V_ep = V_bp1 + V_rp+V_ep

La chute de tension V_rp aux bornes de R₃ est immédiate :

V_rp=I_bp1xR₃=4mAx33=132mV=0,132V

La chute de tension V_ep se calcule de la même manière, en se rappelant toutefois que la résistance R_e n'est pas seulement traversée par le courant de base I_b1, mais aussi par celui du collecteur I_c1 (voir les flèches de la figure 8). On a donc :

V_ep=(I_bp1+I_cp1)xR_e = (4mA+280mA)x4,7 = 284mAx4,7 = 1334mV = 1,334V

On a enfin:

V_ep=V_bp1+V_rp+V_ep = 0,24+0,132+1,334 = 1,706V

La résistance d'entrée de l'étage est donc :

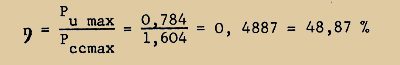
Ceci est donc la valeur de la résistance que présente chaque transistor pendant l'alternance où il conduit : c'est-à-dire la valeur de la résistance sur laquelle sont fermées alternativement les deux moitiés du secondaire Te.

On peut maintenant déterminer le rapport de transformation "ne" que devra avoir le transformateur d'entrée. En supposant que l'on puisse négliger les résistances des enroulements primaire et secondaire et que la résistance de charge dynamique del'étage driver doit être par exemple :

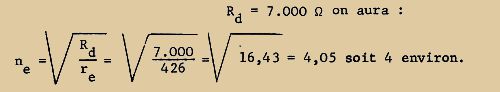
Le nombre de spires du primaire devra donc être quatre fois plus grand que le nombre de spires d'un demi-enroulement du secondaire.

Pour piloter l'étage final de la figure 6, le secondaire de Te devra délivrer une tension maximum égale à V_ep  = 1,706 V avec un courant maximum égal à I_bp = 4mA, ce qui signifie que les valeurs maxima des composantes alternatives de tension et de courant de collecteur de l'étage pilote (driver) devront être respectivement de :

V_cp = V_ep x ne = 1,706 x 4 = 6,824V

I_cp = I_bp / ne = 4/4 = 1mA

Ceci étant les valeurs de crête de la tension et du courant (supposés sinusoïdaux), la puissance nécessaire pour piloter l'étage final sera donnée par la formule :

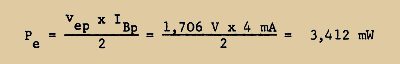
C'est donc la puissance que devra délivrer l'étage pilote.

Avec cet exemple numérique, nous avons complètement terminé l'étude des amplificateurs de puissance push-pull, classe B ou AB, utilisés couramment en radio. Ces amplificateurs peuvent être de puissance plus grande ou plus petite que celle considérée dans l'exemple numérique, le principe de fonctionnement restera toujours le même.

---

REPONSE AUX EXERCICES DE RÉVISION DE LA 20^ème LECON THEORIQUE

1°- Dans un étage push-pull, on doit utiliser deux transistors identiques.

2°- Parce que ces alternances sont délivrées respectivement par l'un puis par l'autre transistor qui travaillent dans les mêmes conditions.

3°- Dans un étage amplificateur classe B , les deux transistors sont polarisés tous les deux au cut-off.

4°- Aucune  puisque les deux transistors sont polarisés au cut-off.

5°- Non, ils conduisent alternativement : l'un pendant l'alternance négative, l'autre pendant l'alternance positive.

6°- Oui, en utilisant un haut-parleur à impédance élevée et qui comprend une bobine avec une prise centrale, ou bien en utilisant un schéma où les deux transistors ne sont plus branchés en opposition de phase mais en série.

7°- Parce qu'il est pratiquement impossible d'obtenir un transistor NPN et un PNP de caractéristiques identiques.

8°- La puissance dissipée sur les collecteurs des transistors dans un étage classe B, atteint sa valeur maximum quand l'amplitude Icp du courant de collecteur est égale à 0,636 fois Icmax.

9°- Parce que le point de fonctionnement ne reste pas dans la zone "interdite" mais y transite uniquement pendant l'alternance où le transistor conduit.

---

EXERCICES DE RÉVISION SUR LA 21^ème LECON THEORIQUE

1°- Qu'appelle-t-on caractéristique  "composée" ?

2°- Pourquoi fait-on travailler les transistors d'un étage de sortie push-pull en classe AB et non en classe B ?

3°- Pourquoi ne peut-on pas mettre de condensateur d'émetteur dans un étage push-pull ne fonctionnant pas en classe A ?

4°- Est-ce que la caractéristique composée est parfaitement symétrique par rapport au point de repos ?

5°- Dans un étage de sortie push-pull, lorsqu'un transistor est au cut-off, la tension de son collecteur reste-t-elle constante ?

6°- Pour une tension d'alimentation de 9 V, quelle serait la tension maximum de collecteur atteinte ?

7°- Dans un étage de sortie, faut-il s'imposer au primaire du transformateur d'entrée la forme de la tension ou celle du courant ?

8°- Qu'appelle-t-on "distorsions initiales" ?

9°- Comment peut-on éviter ces "distorsions initiales" ?

Fin de la leçon 21

---

LECON 22

1 – LARGEUR DE BANDE ET FRÉQUENCES DE COUPURE

Dans tous les étages amplificateurs à transistors étudiés jusqu’à maintenant, nous avons considéré que le signal appliqué à l’entrée de l’amplificateur avait comme fréquence 50Hz. Cette valeur a été supposée uniquement pour fixer les idées et aurait pu être complètement ignorée puisque toutes les constructions graphiques peuvent être faites sans connaître la fréquence du signal.

Or en réalité, un amplificateur ne peut amplifier que certaines fréquences comprises entre des valeurs plus ou moins proches l’une de l’autre.

Pour étudier le comportement d’un amplificateur du point de vue fréquence du signal appliqué, je vais tout d’abord vous décrire une expérience qui sert à déterminer ce que l’on appelle la "courbe de réponse" d’un amplificateur.

Pour réaliser cet essai, il faut avoir à sa disposition un générateur basse fréquence (car on étudie actuellement des amplificateurs BF) et qui permette de faire varier la fréquence du signal dans toute la gamme qui nous intéresse (par exemple de 20Hz à 20kHz) et de régler l’amplitude à la valeur désirée. Ces réglages sont effectués à l’aide des boutons indiqués par f (fréquence) et A (amplitude) dans le schéma synoptique de la figure 1.

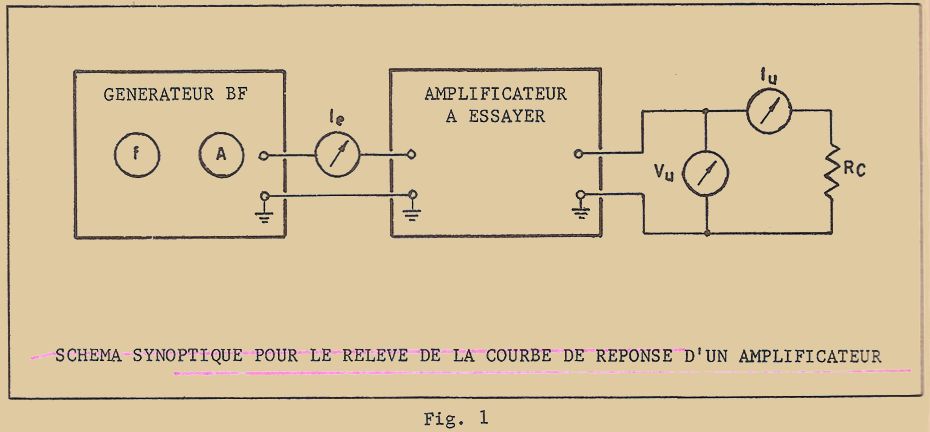
Les bornes de sortie du générateur sont reliées à celles d’entrée de l’amplificateur à essayer et qui a été représenté symboliquement par un rectangle. Les bornes de sortie de l’amplificateur sont reliées à la résistance de charge R_c qui représente par exemple le haut-parleur.

Pendant tout le temps de l’essai, on maintiendra constante la valeur du courant d’entrée de l’amplificateur, mesuré par l’appareil I_e, et pour chaque valeur de la fréquence du signal, on notera les valeurs du courant ou de la tension de sortie (utilisation) mesurées respectivement par le milliampèremètre I_u ou le voltmètre V_u.

La courbe de réponse s’obtient en construisant le graphique de la manière suivante. On porte sur l’axe horizontal les valeurs de la fréquence pour lesquelles on fait la mesure et en correspondance à chacune de ces valeurs, on porte vers le haut les valeurs du courant de sortie (ou de la tension) ou si l’on préfère les valeurs du gain obtenu en divisant la valeur du courant de sortie par la valeur du courant d’entrée, la fréquence restant constante pendant la mesure.

Le graphique obtenu à l’allure typique de la figure 2. Il est en fait constitué de trois régions bien distinctes : la région centrale, presque horizontale, et deux régions décroissant rapidement vers le bas. La signification physique d’une telle courbe se comprend : la région droite indique que le gain de l’amplificateur reste constant pour toutes les fréquences comprises dans cette région. Tandis que pour des fréquences inférieures à une certaine valeur et supérieure à une certaine autre valeur, la courbe descend, ce qui signifie que le gain décroît rapidement.

En d’autres termes, la région centrale droite définit la Bande de fréquence dans laquelle l’amplificateur fonctionne normalement ; en dehors de cette région, on ne peut plus l’utiliser car son gain descend à des valeurs inacceptables.

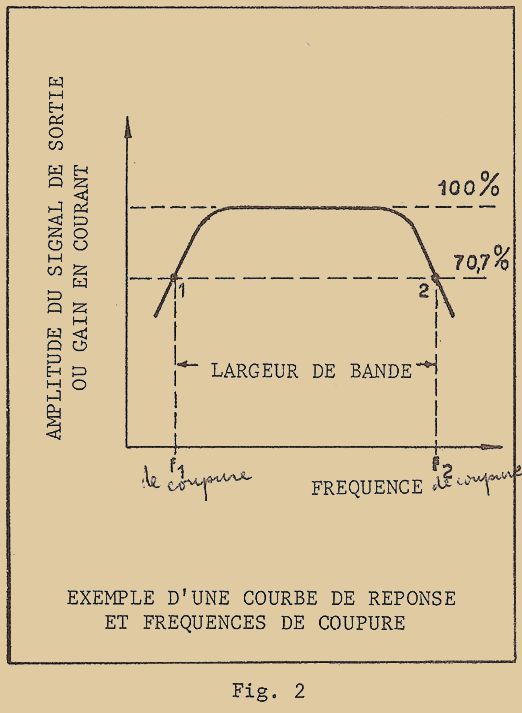
Comme les deux régions inclinées se raccordent à la région centrale d’une façon relativement "douce", les fréquences qui délimitent la région centrale sont mal définies.

On a donc décidé par convention de considérer les points de la courbe pour lesquels le gain se réduit à 70,7% de la valeur de la région centrale (considérée à 100%). Je vous ai repéré ces deux points sur la figure 2, par "1" et "2". Les fréquences f₁ et f₂ qui correspondent à ces points, prennent respectivement le nom de fréquence de coupure inférieure et fréquence de coupure supérieure. Les deux fréquences délimitent la bande de fréquence où l’amplificateur peut être utilisé.

On peut maintenant définir la largeur de bande de l’amplificateur souvent repérée par la lettre B et qui est la différence entre les deux fréquences de coupure : B = f₂ – f₁.

Il serait trop long d’expliquer les raisons pour lesquelles on a défini ainsi les fréquences de coupure. Il suffit seulement de remarquer qu’une réduction du gain en courant (ou en tension) à 70,7% de la valeur correspondant à la région centrale, équivaut à une réduction du gain en puissance de 50% (c’est-à-dire de moitié).

On peut donc dire que les fréquences de coupure sont telles que la puissance de sortie se réduit à la moitié de ce qu’elle est pour les fréquences centrales, lorsque le courant (ou la tensio) de commande à l’entrée reste constant pour toutes les fréquences.

Les fréquences de coupure sont des valeurs caractéristiques de l’amplificateur et ne dépendent exclusivement que des composants du circuit.

Pour fixer les idées, nous dirons que pour un amplificateur BF normal, la valeur de f₁ est comprise entre 50 et 200Hz et que la valeur de f₂ est comprise entre 5kHz et 10kHz. Pour un amplificateur à haute fidélité, f₁ est comprse entre 20Hz et 50Hz et f₂ entre 10kHz et 15kHz.

Après avoir défini ce qu’étaient les fréquences de coupure, nous allons voir comment on peut les déterminer théoriquement à partir des valeurs des composants qui constituent l’amplificateur.

1 – 1 FRÉQUENCE DE COUPURE SUPÉRIEURE

Nous avons vu dans la théorie 12 que le coefficient d’amplification en courant β correspondait au paramètre h_21e et qu’il était défini par :

β = h_21e = i₂/i₁

où i₁ indique l’accroissement du courant de base provoqué par la variation de la résistance de polarisation de la base (R_B - figure 5 - théorique 12) et i₂ l’accroissement correspondant du courant de collecteur.

Au lieu de provoquer un accroissement permanent du courant de base comme c’était le cas dans la théorie 12, nous pouvons provoquer un accroissement qui se répète périodiquemenr en appliquant un signal sinusoïdal sur la base. Dans ce cas en effet, à chaque période du signal, le courant de base subit un accroissement et une diminution par rapport à sa valeur de repos. Le courant de collecteur va suivre ces variations et subira un accroissement et une diminution périodique.

La valeur de β peut donc être calculée aussi à l’aide de la même formule, ou i₁ et i₂ seront les amplitudes des accroissements et des diminutions périodiques du courant de base et du courant de collecteur, c’est-à-dire leurs excursions, ou si l’on préfère les amplitudes des "composantes alternatives" des deux courants.

L’avantage d’une telle mesure du coefficient d’amplification est de pouvoir faire varier la fréquence du signal et de voir comment varie la valeur de β lorsque croît la fréquence.

On peut utiliser pour fixer les idées, le circuit indiqué sur la figure 3. On règle le point de repos du transistor à la valeur désirée, puis on injecte sur la base du signal de sortie du générateur BF à travers une résistance R₁ de forte valeur (100kΩ par exemple) pour avoir une commande en courant. La valeur de i₁ sera alors indiquée par l’appareil de mesure pour courant alternatif I₁ et i₂ par I₂ (milliampèremètre pour courant alternatif aussi). Ce dernier ne doit seulement être sensible qu’au courant alternatif du collecteur et ne pas mesurer la composante "continue", ce qui peut se faire en pratique par un artifice de montage qu’il serait trop long d’expliquer ici.

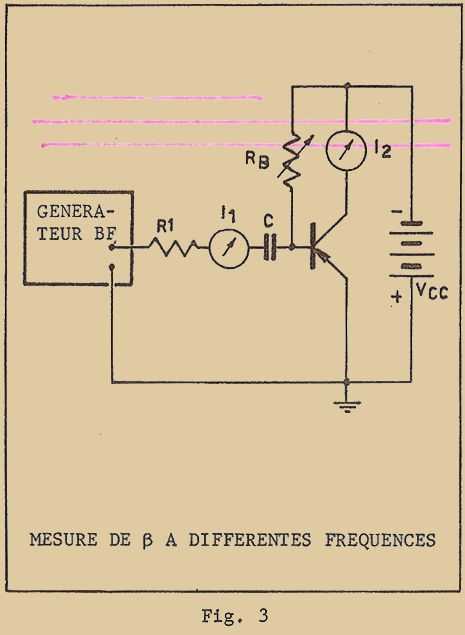
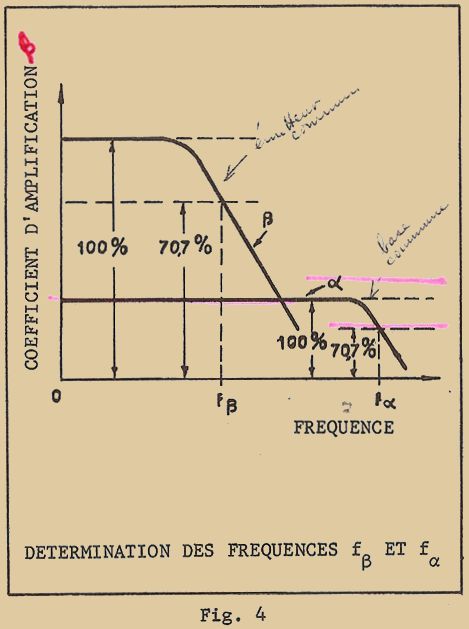
La valeur de β obtenue à l’aide de cette méthode est pratiquement la même que celle que l’on avait obtenue dans la 12^ème théorie si la fréquence du signal appliqué à la base est relativement faible. Si l’on augmente la fréquence, on trouve que β commence à diminuer à partir d’un certain moment (fig 4).

Par analogie avec ce qui a été dit auparavant, on peut définir une certaine fréquence de coupure propre au transistor en émetteur commun (indiqué en général par f_β ou f_αe), fréquence pour laquelle la valeur de β se réduit à 70,7% de sa valeur aux fréquences basses.

Si l’on procède de même, mais pour le transistor en base à la masse, on trouve que le coefficient α commence à diminuer lorsque la fréquence atteint une certaine valeur (voir figure 4). On définit de la même manière, la fréquence de coupure propre du transistor en montage base commune et que l’on indique par f_α (ou f_αb).

La fréquence f_α est toujours supérieure à f_β ; on trouve que f_α est environ β fois plus grande que f_β. Ces valeurs indiquent la fréquence maximum à laquelle le transistor peut être utilisé comme amplificateur, respectivement en montage base à la masse et émetteur à la masse, et représentent donc aussi la fréquence de coupure supérieure f₂ de l’amplificateur.

Comme normalement les transistors sont utilisés en émetteur commun, on peut dire que la fréquence de coupure supérieure de l’amplificateur coïncide avec la fréquence f_β du transistor utilisé.

La raison de la diminution de la valeur du coefficient d’amplification réside principalement dans les phénomènes complexes de la conduction à l’intérieur du transistor, ce qui a été déjà étudié en son temps.

En quelques mots, on peut rappeler qu’à cause de la capacité d’entrée et de sortie du transistor (théorique 12) le courant de collecteur suit le courant de commande avec un certain retard, et lorsque le courant de base varie trop rapidement (fréquences élevées), le courant du collecteur ne peut plus suivre ces variations rapides et l’amplification du transistor tombe à des valeurs très faibles.

Pour les transistors utilisés en basse fréquence, la valeur de f_β est comprise en général entre 6kHz et 15kHz ; f_α par contre est comprise entre 500kHz et un peu plus de 1 MHz. Ainsi :

pour le transistor OC71 on a : f_β = 10kHz et f_α = 500kHz environ.

pour le transistor SFT151 on a : f_β = 30kHz et f_α = 1,2 MHz environ

pour le transistor SFT153 on a : f_β = 30kHz et f_α = 2,4 MHz environ

Prenons par exemple le schéma de la figure 5 (qui est le même que celui de la figure 4 théorique 17), la fréquence de coupure du premier étage est de 30kHz environ (transistor SFT151). Si l’on voulait réduire la fréquence de coupure supérieure de l’amplificateur à une valeur plus faible que celle du transistor, il suffirait de placer entre le collecteur et la masse, un condensateur. La valeur d’un tel condensateur Cc devra être d’autant plus élevée qu’on désire une fréquence de coupure faible et que plus faible est la valeur de la résistance de sortie de l’étage. Ceci est en général déterminé en pratique par voie expérimentale.

1 – 2 FRÉQUENCE DE COUPURE INFÉRIEURE

La fréquence de coupure inférieure d’un étage est déterminée par la valeur de la capacité placée en parallèle sur la résistance d’émetteur. Cette capacité a en effet pour rôle de créer une voie facile pour la composante alternative du courant de collecteur et d’éviter une forte réduction de gain qui est introduit par la présence de la résistance d’émetteur (revoir théorique 17).

En se rappelant maintenant qu’un condensateur de capacité C se comporte vis-à-vis du courant alternatif comme une "résistance" (on dit réactance) de valeur X_c = 1/(2πfC) on en déduit qu’il laissera passer le courant alternatif d’autant moins facilement que la fréquence sera plus faible.

Ainsi, si l’on diminue progressivement la fréquence du signal appliqué à l’amplificateur de la figure 5, le condensateur C_E va s’opposer de plus en plus au passage de la composante alternative du courant de collecteur et son action va devenir de moins en moins efficace.

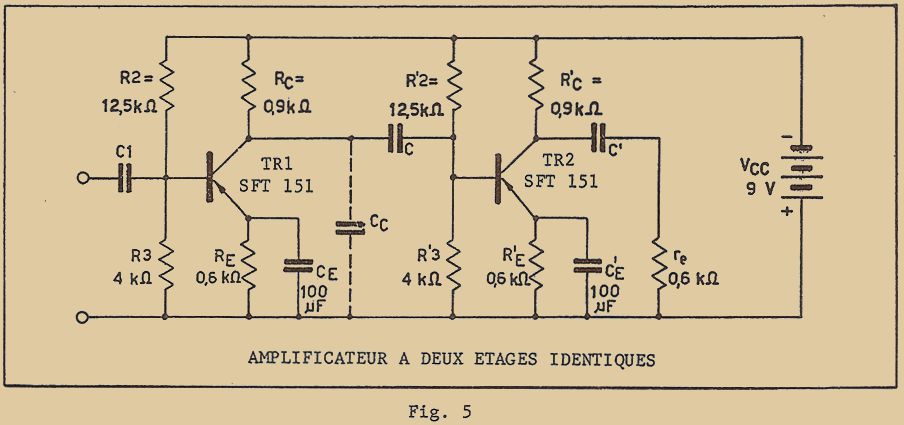
A un certain moment, il ne pourra plus éviter la contre-réaction dûe à R_E et le gain de l’étage va commencer à diminuer. Il existe donc une certaine fréquence pour laquelle le gain se réduit à 70,7% de la valeur pour les fréquences moyennes : cette fréquence sera donc considérée comme fréquence de coupure inférieure dûe à C_E. Elle peut être déterminée facilement à l’aide de la formule suivante :

f₁ = 159/(R_E C_E) x (1 + (β x R_E)/(r_B+R_A))

et inversement, si l’on désire obtenir une certaine valeur de la fréquence de coupure f₁, la valeur de CE devra être :

C_E = 159/(R_E x f₁) x (1 + (β x R_E)/(r_B+R_A))

Dans ces deux formules, on doit toujours exprimer la résistance en kΩ, la capacité en µF et la fréquence enHz. Il faut encore remarquer que r_B représente la résistance d’entrée du transistor seul tandis que R_B est égale à la mise en parallèle de R_B de l’étage considéré (égale elle-même à R₂ en parallèle avec R₃) et de la résistance de sortie rs de l’étage précédent. Si l’étage considéré n’est pas précédé par un autre étage (comme c’est le cas du premier étage de la figure 5) alors R_B = R_B.

Examinons par exemple, le second étage de la figure 5. On avait trouvé dans la 16ème leçon de théorie que R_B = 3,03kΩ et que rs coïncidait pratiquement avec la valeur de R_c, soit 0,9kΩ ; on a donc :

R_B = (R_B x r_s)/(R_B+r_s ) = (3,03 x 0,9)/(3,03+0,9) = 2,727/3,93 = 0,693kΩ environ

On a d’autre part :

R_E = 0,6kΩ, C_E = 100 µF, β = 49,5.

La valeur de f₁ est donc :

f₁ = 159/(0,6 x 100) x (1 + (49,5 x 0,6)/(0,75+0,693)) = 159/60 x (1 + 29,7/1,443) = 2,65 x (1 + 20,6) = 2,65 x 21,6 = 57,24Hz

Dans le cas du 1er étage, on a R_B = R_B = 3,03kΩ et on trouverait que f₁ = 23Hz environ.

Un autre élément qui peut limiter l’amplification aux fréquences basses et qui peut aussi déterminer la fréquence de coupure inférieure est le condensateur C de liaison entre étages (ou entre l’étage et la charge) (figure 5).

En effet, en diminuant la fréquence du signal, C s’oppose toujours de plus en plus au passage du courant alternatif, délivré par TR₁ pour piloter TR₂. On voit donc qu’en diminuant la fréquence on trouvera certainement une valeur de f₁ pour laquelle le courant de commande de TR₂ va se réduire à 70,7% de sa valeur normale. Cette fréquence représentera donc la fréquence de coupure inférieure.

La valeur de f₁, déterminée par le condensateur de liaison est donné par la formule :

f₁ = 159/(C x (r_s+r_e))

ou bien si l’on se fixe la valeur de f₁, la valeur de C devra être :

C = 159/(f₁ x (r_s+r_e))

Dans cette formule, r_s est la résistance de sortie de l’étage qui précède C et r_e, la résistance d’entrée de l’étage qui suit C ; r doit être exprimé en kΩ, C en µF et f en Hz.

A remarquer encore que la fréquence de coupure inférieure est d’autant plus basse que la capacité utilisée pour la liaison est plus grande.

Dans le cas de la figure 5 par exemple, rs est presque égal à RC, soit de 0,9kΩ et re = 0,6kΩ. Si on utilise un condensateur de liaison C de 0,5µF, on a une fréquence de coupure de :

f₁ = 159/(0,5 x (0,9+0,6)) = 159/(0,5 x 1,5) = 159/0,75 = 212Hz

Des deux fréquences de coupure ainsi obtenues avec C_E et C, on devra prendre celle qui a la valeur la plus grande, puisque c’est celle qui limite le plus la bande passante. Pour le premier et pour le second étage de la figure 5 (car ils sont égaux) on prendra comme fréquence de coupure inférieure, la valeur f₁ = 212Hz

Lorsque la liaison entre deux étages, ou entre l’étage et sa charge est du type inductif (par transformateur), on démontre que la fréquence de coupure inférieure dépend de l’inductance du primaire du transformateur et est d’autant plus basse que la valeur L de cette inductance est plus grande.

La formule à utiliser est alors :

f₁ = (159 x R)/L ou L = (159 x R)/f₁

avec f₁ en Hz, R en kΩ et L en Henrys.

R représente la résistance équivalente à la mise en parallèle de la résistance de sortie r_c du transistor relié au primaire du transformateur et de la résistance d’entrée r_e de l’étage suivant ramenée au primaire, c’est-à-dire multipliée par n2 ; on a donc :

R = (r_c x n² r_e)/(r_c + n² r_e)

Dans le cas de l’exemple de la figure 6 théorique 17, on a n² = 2 (car n = 1,41) et r_e = 0,75kΩ ; comme rc = 14kΩ environ, on trouve R = 1,355kΩ environ. Si l’inductance primaire du transformateur est de 4 H (Henry), la fréquence de coupure est :

f₁ = (159 x 1,355)/4 = 53,86Hz

S’il s’agit d’un étage de sortie, r_e n’est autre que la résistance de charge R_S qui ramenée à l’entrée est : R_p = n²s x R_s et qui est toujours plus faible que celle de sortie r_c du transistor de sortie. Dans ces conditions, la mise en parallèle de r_c et de R_p est équivalente à R_p à peu de chose, on peut donc prendre dans la formule précédente R = R_p.

Reprenons l’exemple du schéma de la figure 6 ; si nous désirons avoir une fréquence de coupure de 20Hz, avec R = R_p = 20Ω = 0,020kΩ, la valeur de L devra être :

L = (159 x R)/f₁ = (159 x 0,02)/20 = 0,159 H

Cette valeur d’inductance correspond obligatoirement à la moitié du primaire du transformateur de sortie, puisqu’il s’agit d’un amplificateur classe B.

1 – 3 FRÉQUENCE DE COUPURE D’UN AMPLIFICATEUR A PLUSIEURS ÉTAGES.

Pour obtenir les fréquences de coupure f'₁ et f'₂ d’un amplificateur à plusieurs étages en connaissant celles des étages qui le composent, il faut encore distinguer les deux cas suivants :

1) Les étages composants sont tous identiques

Dans ce cas, tous les étages composants ont la même fréquence de coupure inférieure f₁ et la même de coupure supérieure f₂. On a donc :

f'₁ = f₁ x K f'₂ = f₂ / K

K étant un coefficient qui dépend du nombre d’étages et qui est donné par le tableau suivant :

Nombre d’étage	2	3	4	5	6	7	8
Valeur de K	1,56	1,96	2,30	2,59	2,86	3,10	3,32

Par exemple l’amplificateur de la figure 5, est formé de deux étages égaux et pour chacun d’eux on a : f₁ = 212Hz et f₂ = 10kHz. On a dans ce cas :

K = 1,56

f'₁ = f₁ x K = 212 x 1,56 = 330Hz environ

f'₂ = f₂ / K = 10 / 1,56 = 6,4kHz environ

On voit donc, qu’en augmentant le nombre d’étages en cascades, la bande passante totale diminue car f'₁ augmente et f'₂ diminue.

2) Les étages composants sont tous différents (leurs fréquences de coupure sont donc toutes différentes)

Dans ce cas on obtient, avec une très bonne approximation, comme fréquence de coupure inférieures de l’amplificateur celle la plus élevée des fréquences de coupure inférieures des étages composants et comme fréquence de coupure supérieure celle la plus faible des étages composants. En effet, ce sont ces fréquences-là qui limitent le plus la bande passante totale.

---

EXERCICES DE RÉVISION SUR LA 22^ème LEÇON THÉORIQUE

1 – Quels sont les appareils de mesure (de base) que l’on doit utiliser pour relever la courbe de réponse d’un amplificateur ?

2 – Comment doit-on opérer lors du relevé d’une courbe de réponse ?

3 – Qu’exprime la courbe de réponse ?

4 - Comment définit-on la fréquence de coupure d’un amplificateur ?

5 – Comment est définie la bande passante d’un amplificateur ?

6 – De quoi dépend la fréquence de coupure supérieure d’un étage ?

7 – De quoi dépend la fréquence de coupure inférieure d’un étage à liaison par capacité ?

8 – De quoi dépend la fréquence de coupure inférieure d’un étage à liaison par transformateur ?

9 – Comment est la bande passante d’un amplificateur à plusieurs étages identiques, par rapport à celle d’un seul étage ?

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 21ème LEÇON THÉORIQUE

1 – On appelle "caractéristique composée", la caractéristique qui résulte de la composition des deux caractéristiques relatives aux transistors qui travaillent en opposition de phase.

2 – Si l’on fait travailler les transistors d’un étage de sortie push-pull en classe AB au lieu de la classe B, c’est pour éviter ce que l’on appelle les distorsions "initiales" dûes au fait que les transistors ne conduisent pas pour de faibles tensions appliquées à leur base.

3 – Si l’on place un condensateur sur les émetteurs d’un étage push-pull ne fonctionnant pas en classe A, on tend alors à polariser les émetteurs avec comme conséquence la distorsion du signal de sortie.

4 – La caractéristique composée est symétrique par rapport au point de repos : de ce fait, les deux alternances de sortie sont parfaitement identiques

5 – Non, la tension de collecteur du transistor bloqué ne reste pas constante, mais dépasse cette valeur à cause de la tension induite dans la moitié du primaire correspondant.

6 – Pour une alimentation de 9 V, la tension de collecteur atteinte pourrait être au maximum de 18 V.

7 – Dans un étage de sortie, on s’impose la forme de la tension appliquée au primaire du transformateur d’entrée.

8 - On appelle "distorsions initiales", les distorsions du courant de base et du courant de collecteur et qui sont dûes à la courbure de la caractéristique d’entrée.

9 – On peut les éviter en polarisant légèrement les bases des deux transistors.

Fin de la leçon 22

---

LECON 23

1 – AMPLIFICATEURS SÉLECTIFS

Dans la leçon précédente, nous avons vu qu’un amplificateur ne pouvait fonctionner que dans une gamme de fréquence limitée du côté haut par la fréquence de coupure du transistor et du côté bas par les composants de liaison entre étages.

La bande passante d’un tel amplificateur est quand même très large et on peut faire en sorte que la fréquence de coupure supérieure soit mille fois plus grande que la fréquence de coupure inférieure (c'_e st par exemple le cas d’un amplificateur dont la bande s’étend de 20Hz à 20kHz). Pour cette raison, l’amplificateur est appelé Apériodique, car il n’amplifie pas de fréquence préférentielle.

En utilisant un circuit de charge appropriée, à la place de la seule résistance (placée directement dans la connexion du collecteur, ou couplée à ce dernier à l’aide d’un condensateur ou d’un transformateur), on peut obtenir une bande passante extrêmement réduite par rapport à celle d’un amplificateur apériodique, si bien que l’on peut dire que l’amplificateur n’amplifie qu’une seule fréquence bien déterminée. Ce type d’amplificateur est appelé Sélectif (ou encore accordé) à cause de sa propriété de sélectionner et d’amplifier une seule fréquence parmi toutes celles qui sont injectées à son entrée.

Le schéma le plus simple d’un amplificateur sélectif est celui qui est indiqué à la figure 1 où l’on a placé dans le circuit du collecteur un circuit résonnant composé d’une inductance L, d’une capacité C et d’une résistance R placées toutes les trois en parallèle. (On ne considère ici qu’un montage en émetteur commun, mais tout ce qui va être dit reste valable pour les autres montages, compte tenu d’une très faible différence).

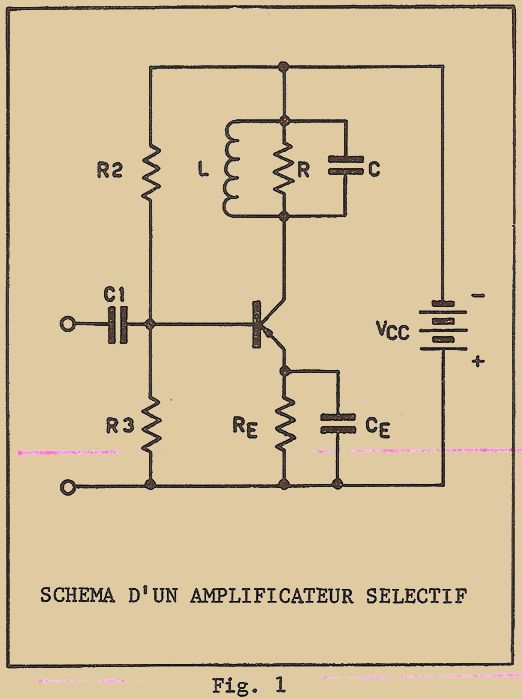
Avant de considérer le fonctionnement du circuit de la fig 1, il convient de rappeler brièvement les propriétés d’un circuit résonnant. Il suffit pour cela d’alimenter le circuit résonnant à l’aide d’un générateur de signaux (du type de celui vu dans la précédente leçon) à travers une résistance R₁ de forte valeur (figure 2a).

Supposons maintenant que nous réglions la tension de sortie du générateur de manière que le courant indiqué par l’appareil de mesure I ait une certaine valeur, par exemple 1mA et que nous mesurions avec le voltmètre V la tension qui apparait aux bornes du circuit résonnant. Si nous répétons ces mesures pour différentes valeurs de la fréquence (en maintenant constant le courant à l’entrée), et si nous notons pour chaque fréquence la valeur de la tension correspondante, nous pouvons tracer un graphique en portant sur l’axe horizontal les valeurs de la fréquence et sur l’axe vertical les valeurs correspondantes de la tension.

Le graphique ainsi obtenu prend le nom de courbe de résonnance du circuit considéré et a l’aspect typique de la figure 2b en forme de cloche ou comme on dit quelquefois en "chapeau de gendarme"

La fréquence à laquelle la courbe atteint le sommet (point 3 de la figure 2b) est appelé fréquence de résonance du circuit et est en général indiquée par le symbole f_o

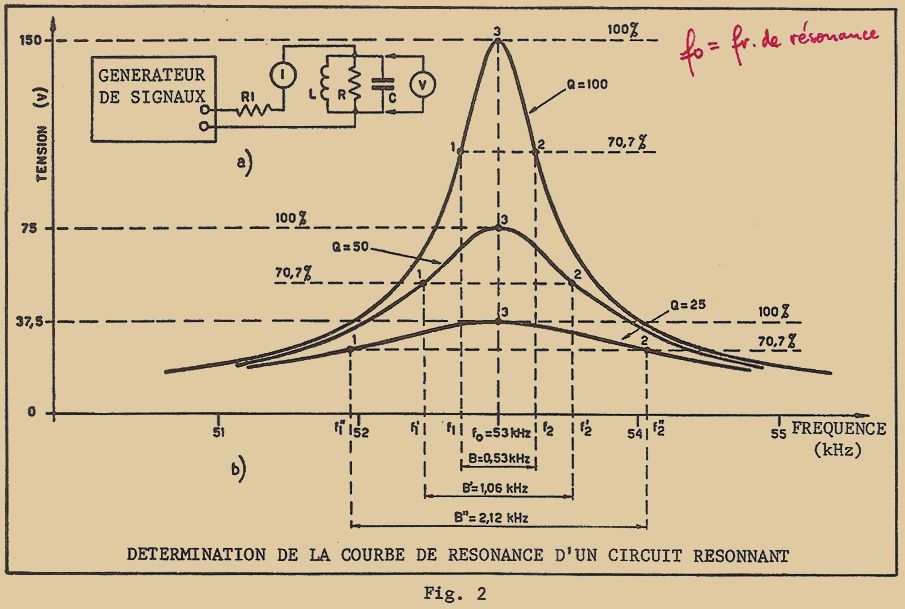
La valeur de f_o dépend uniquement des valeurs de l’inductance L et de la capacité C et est donnée par la formule :

f_o = 159/√LxC

où :

f_o est exprimé en Hz quand L est exprimée en H et C en µF
f_o est exprimé enkHz quand L est exprimée en mH et C en nF
f_o est exprimé en MHz quand L est exprimée en µH et C en pF

Il faut encore se rappeler que 1nF (nanofarad) est égal à 1.000pF ; ce sous multiple du farad est souvent indiqué en kilopicofarad (kpF) selon la dénomination américaine.

Prenons un exemple : supposons que dans le schéma de la figure 2a, nous ayons : L = 4,5 mH et C = 2nF. La fréquence de résonnance est alors :

f_o = 159/√(4,5x2) = 159/√9 = 159/(3 ) = 53Hz

On démontre qu’à la fréquence de résonance la réactance X_L de l’inductance est égale à la réactance X_C de la capacité. Ces réactances sont données par les formules :

X_L = (f x L)/159 et X_C = 159/(f x C)

où X_L et X_C sont exprimées en kΩ et les autres grandeurs sont exprimées respectivement comme suit :

f en Hz	L en H	C en µF
f en kHz	L en mH	C en nF
f en MHz	L en µH	C en pF

Je vous rappelle que la formule de base qui donne la fréquence de résonance d’un circuit est :

f_o = 1/(2π√(LxC))

où :

π= 3,14
f_o est donnée en Hz
L est exprimée en H
C est exprimée en F

Si vous avez oublié les unités des autres formules, vous pouvez toujours reprendre cette dernière formule et vous serez certain de ne pas commettre d’erreur.

1 Henry = 10³ mH = 10⁶ µH

1 Farad = 10⁶µF = 10⁹nF = 10⁹kpF = 10¹²pF

Prenons un exemple : soit f_o = 53kHz L = 4,5 mH C = 2nF

X_L = (f x L)/159 = (53 x 4,5)/159 = 238,5/159 = 1,5kΩ

X_C = 159/(f x C) = 159/(53 x 2)= X_C = 159/106 = 1,5kΩ

Ces valeurs des réactances à la fréquence de résonnance (X_L = X_C) sont indiquées par le symbole X_o

Pour expliquer la forme de la courbe de résonnance, il faut remarquer que les valeurs des tensions portées sur le graphique de la figure 2b sont données par le produit du courant que l’on fait circuler dans le circuit (dont la valeur est mesurée par l’appareil I et qui est maintenu constant pour toutes les fréquences) par l’impédance du circuit.

Or, le circuit résonnant est formé de trois éléments en parallèle ; son impédance est donnée par la mise en parallèle de la résistance R, de la réactance X_L de l’inductance et de la réactance X_C de la capacité. Sa valeur est calculée à l’aide d’une formule assez complexe que je vous indique ci-dessous, mais qu’il est inutile d’apprendre par cœur.

Z = 1/(1/R² + (Cω - 1/(Lω)²)^1/2

ω se lit ici "omega"

où Z est l’impédance exprimée en Ω, si R est en Ω, C en Farad et L en Henry.

ω = 2πf = 2 x 3,14 x f = 6,28 f (ω est la pulsation)

f étant la fréquence exprimée en Hz.

Les résultats de cette formule indiquent qu’un circuit tel que celui de la figure 2a, se comporte de trois façons différentes, suivant que la fréquence du courant qui le traverse est égale à la fréquence de résonnance f_o, qu’elle est plus basse que f_o ou plus élevée que f_o.

A la fréquence de résonnance, le circuit résonnant se comporte comme une simple résistance de valeur égale à R. On aurait pu prévoir ce résultat intuitivement en sachant qu’à la fréquence f_o, les réactances de L et de C sont égales et opposées, leurs effets se détruisent mutuellement, et pour le circuit, tout se passe comme si L et C n’existaient pas.

A une fréquence inférieure à la fréquence de résonance, le circuit se comporte comme une résistance R qui aurait en parallèle à ses bornes une inductance L’ dont la valeur croît au fur et à mesure que la fréquence considérée devient plus basse que la fréquence de résonance. On peut encore expliquer ceci en disant que lorsque la fréquence diminue, la réactance X_L diminue (revoir les formules qui donnent X_L et X_C) tandis que X_C augmente. Ainsi, à une fréquence plus basse que f_o, le courant passe plus facilement à travers l’inductance qu’à travers la capacité, ce qui en d’autres termes signifie que l’effet de l’inductance prédomine sur celui de la capacité.

Pour des fréquences plus élevées que f_o, le circuit se comporte comme une résistance R qui aurait une capacité C’ en parallèle à ses bornes dont la valeur diminuerait au fur et à mesure que la fréquence deviendrait plus grande que f_o. Ce fait peut s’expliquer en pensant que lorsque la fréquence augmente, X_L augmente aussi tandis que X_C diminue. En raisonnant comme tout à l’heure, on en déduit que le courant passe plus facilement au travers de la capacité et l’effet de celle-ci devient prédominant.

Les trois cas que nous venons d’examiner sont reportés à la figure 3. A la fréquence f_o, la tension aux bornes du circuit est égale au produit du courant par la valeur de R ; si par exemple R = 150kΩ et le courant égal à 1mA (comme supposé) la tension correspondant au point 3 de la figure 2b sera :

1mA x 150kΩ= 150V

Pour des fréquences différentes de f_o, l’impédance du circuit sera inférieure à R parce qu’en parallèle sur R, il y aura la réactance de L’ ou de C’ ; ainsi la tension sera inférieure à 150V et diminuera très rapidement au fur et à mesure que l’on va s’éloigner de la fréquence de résonance.

Si dans le circuit de la figure 2a, on change la valeur de R, par exemple en la diminuant à 75kΩ, la tension aux bornes du circuit résonnant ne sera plus que de 75V, c'est-à-dire qu’elle a diminué de moitié par rapport au cas précédent. La courbe de résonnance est plus basse que la première. Dans les deux cas cependant, la fréquence de résonnance est toujours 53kHz, car f_o ne dépend que de L et de C, mais pas de R.

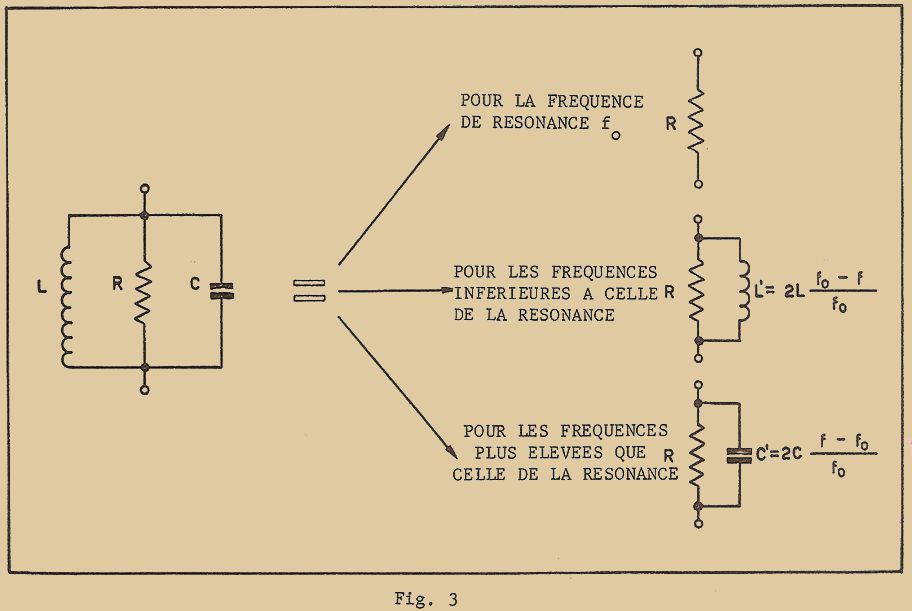
De la valeur de R dépend au contraire le facteur de qualité Q du circuit résonnant (qu’on appelle aussi coefficient de qualité, ou coefficient de surtension) et qui est défini comme étant le rapport de R et de X, et dont le symbole est Q.

Dans le cas de l’exemple, on a :

Q = R/X_o = (150kΩ)/(1,5kΩ) = 100

Dans le cas où R = 75kΩ on aurait Q = 75 / 1,5 = 50. Plus la valeur de R est élevée, plus la valeur de Q est grande et plus la courbe de résonnance est pointue, comme on peut le voir à la figure 2b.

La définition de la fréquence de coupure, vue dans la précédente leçon peut être appliquée à la courbe de la figure 2. On peut ainsi définir les points 1 et 2 (fréquences f₁ et f₂), pour lesquels l’amplitude de la courbe se réduit à 70,7 % de l’amplitude maximum correspondant à la fréquence de résonance (point 3).

Dans le cas d’un circuit résonnant, les fréquences de coupure sont toujours très voisines de la fréquence de résonance ; pour cette raison on préfère donner comme valeurs caractéristiques du circuit, la bande passante B (égale comme nous l’avons vu à la différence f₂ – f₁) ainsi que la fréquence de résonnance f_o au lieu des valeurs seules de f₁ et f₂ comme on le faisait pour les circuits apériodiques.

La bande passante est étroitement liée au facteur de qualité Q du circuit, et sa valeur est donnée tout simplement par la formule

B = f_o/Q

où B est exprimé dans les mêmes unités que f_o.

Dans l’exemple, on a f_o = 53kHz, la bande passante sera pour un Q = 100 de :

B = 53/100 = 0,53kHz

Pour un Q = 50 :

B = 53/50 = 1,06kHz

On voit ainsi qu’en diminuant la valeur de Q on augmente la bande passante, mais on diminue l’amplitude de la courbe de résonnance. Ainsi, pour avoir une large bande passante, on doit avoir une faible valeur de Q, ce qui s’obtient avec une faible valeur de R, ou comme on dit en "amortissant beaucoup" le circuit résonnant. Si l’on veut au contraire obtenir une bande passante étroite, il faut que le circuit soit très sélectif, il faut donc l’amortir très peu, ce qui signifie utiliser une valeur élevée de R, et avoir ainsi une valeur élevée de Q.

Après ce bref rappel sur le fonctionnement d’un dispositif résonnant nous pouvons revenir à l’étude de notre amplificateur sélectif de la figure 1.

1 – 1 ETAGE A CHARGE ACCORDE

Le schéma de la figure 1 peut être utilisé toutes les fois que l’on désire obtenir un amplificateur capable de sélectionner et d’amplifier une seule fréquence ou une bande étroite autour d’une fréquence donnée.

Dans la gamme des récepteurs radio, on a intérêt à utiliser des amplificateurs sélectifs de façon à pouvoir sélectionner parmi toutes les stations celle que l’on désire écouter.

Dans les récepteurs radio les amplificateurs sélectifs sont des amplificateurs H.F. qui peuvent être à fréquence fixe, c'est-à-dire accordés sur une seule fréquence, une fois pour toutes (comme, par exemple, les amplificateurs à fréquence intermédiaire) ou bien ils peuvent être à fréquence variable, de façon à permettre l’accord manuel sur la fréquence désirée (amplificateurs H.F. proprement dits).

Pour obtenir la possibilité d’un accord dans une certaine gamme de fréquence il faut évidemment que le circuit résonnant soit à accord variable, ce qui peut être obtenu en employant un condensateur variable ou bien une inductance à noyau plongeant comme nous le verrons par la suite (accord manuel).

Comme la gamme de fréquences s’étend pour un récepteur radio de quelques centaines dekHz à quelques MHz (grandes ondes, petites ondes, ondes courtes), la fréquence intermédiaire choisie pour les récepteurs à modulation d’amplitude est fixée soit entre 455kHz et 480kHz. Ainsi les bobines des circuits résonnants pourront être du type à air, sans noyau, ou avec noyau en un matériau prévu pour les fréquences radio (aggloméré de poudre de fer très fine et de certains oxydes, dont chaque grain est enrobé dans un isolant (polyfer, sirufer, etc…) ou mieux encore en matériau céramique comme le ferrite.

Le circuit résonnant est en général enfermé dans un blindage métallique relié à la masse de façon à éviter des couplages parasites avec d’autres circuits, et éventuellement des accrochages.

En ce qui concerne les transistors, on ne pourra évidemment pas utiliser les types vus jusqu’à présent, car ils devront avoir des fréquences de coupure de valeur adéquate, soit de l’ordre de 1MHz pour les amplificateurs à fréquence intermédiaire, et de quelques MHz pour les étages d’entrée du récepteur. Etant données les très faibles puissances mises en jeu dans de tels circuits, on n’utilisera évidemment pas des transistors de puissance et les calculs seront faits exclusivement au moyen des paramètres des différents types, en réservant l’emploi des courbes caractéristiques seulement pour la détermination du point de fonctionnement et le calcul des circuits de polarisation.

Pour prendre un exemple, nous allons étudier un amplificateur sélectif à un seul étage F.I. (fréquence intermédiaire) accordé par exemple sur 467kHz et utilisant un transistor SFT 319 monté en émetteur commun et couplé à un second étage identique au premier.

Avant d’examiner le schéma, il faut encore faire quelques remarques. Avant tout, il faut noter que le circuit résonnant se comporte comme une simple résistance à la fréquence de résonance, c'est-à-dire que pour cette fréquence, et pour elle seule, l’amplificateur a comme charge la résistance R placée en parallèle sur L et C et que la droite de charge dynamique n’est autre que celle qui correspond à la valeur de R.

En second lieu, il faut noter qu’en pratique la résistance R est constituée par la résistance d’entrée de l’étage suivant, et comme celle-ci est en général beaucoup plus faible que la résistance de sortie de l’étage considéré, il faut utiliser un transformateur pour coupler les deux étages si l’on désire conserver un bon gain en puissance. Le primaire d’un tel transformateur ne sera autre que l’inductance L, et le secondaire sera un autre enroulement comportant moins de spires et bobiné sur cette même inductance L.

Ainsi en pratique, le circuit peut être représenté comme sur la figure 4 où l’étage suivant est indiqué par sa seule résistance d’entrée re.

Les résistances R₂, R₃ et R_E servent à la polarisation du transistor et à la stabilisation thermique du point de repos. Les valeurs des résistances indiquées sont telles qu’elles font travailler le transistor avec un courant de collecteur ICo de 1mA et avec une tension entre collecteur et émetteur VCEo de 6 V (recommandée par le constructeur) comme on peut le vérifier facilement d’après les caractéristiques de la figure 5.

En examinant le schéma de la figure 4 on voit que la droite de charge statique correspond à la seule valeur de R_E = 1,5kΩ puisque la résistance de l’enroulement de L est de quelques ohms et peut être parfaitement négligée. Si l’on désire que le point de repos vienne en A on vérifie rapidement que R₂ = 10kΩ et R₃ = 2,7kΩ si la tension d’alimentation VCC est de 7,5 V.

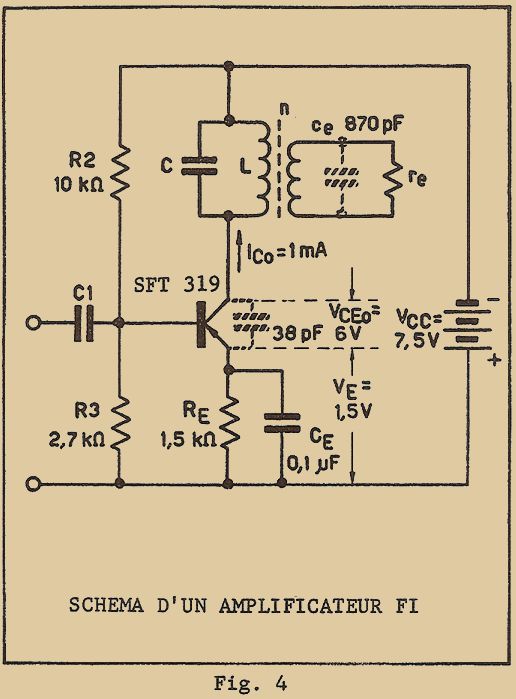
Pour ce point de fonctionnement ; le transistor présente les caractéristiques suivantes :

résistance d’entrée r_e = 0,8Ω
capacité d’entrée ce = 870pF
résistance de sortie r_s = 29kΩ
capacité de sortie c_s = 38pF
transconductance g_m = 35mA/V

Si l’on désire obtenir un gain maximum en puissance, il faudra que la droite de charge dynamique corresponde à la résistance de sortie du transistor (c'est-à-dire 29kΩ dans notre exemple) comme on peut le voir sur la figure 5.

Etant donné que la résistance d’entrée de l’étage suivant (supposé identique au premier) est de 0,8kΩ, on détermine immédiatement quel devra être le rapport de transformation n entre le nombre de spires de l’inductance L et celui de l’enroulement secondaire. En appliquant en effet, la formule vue lors de l’étude des liaisons par induction on trouve :

n = √(r_s/r_e) = √(29/0,8) = √36,25 = 6,02 valeur que l’on arrondira en pratique à 6.

Il reste encore à déterminer les valeurs de l’inductance L et de la capacité C qui constitue le circuit résonnant. Les valeurs doivent être déterminées obligatoirement non seulement suivant la fréquence de résonance désirée, mais aussi suivant la bande passante que l’on se propose d’obtenir.

Soit le cas d’un amplificateur à fréquence intermédiaire (F.I.) d’un récepteur à modulation d’amplitude dont la F.I. soit de 467kHz (elle est quelquefois de 480kHz ou 455kHz). La bande passante doit être de 9kHz car la largeur des canaux des émetteurs à modulation d’amplitude est fixée à 9kHz.

Il faut encore se rappeler que le circuit résonnant formé par la capacité C et par l’inductance L de la figure 4 est amorti non seulement par la résistance d’entrée du transistor de l’étage suivant, mais aussi par la résistance de sortie du transistor considéré. En effet, le transistor de la figure 4 a son collecteur branché à l’extrémité inférieure du circuit résonnant tandis que l’émetteur se trouve branché à l’extrémité supérieure de ce même circuit résonnant au travers du condensateur CE et de la pile d’alimentation.

La pile présente une résistance interne extrêmement faible et le condensateur CE peut être considéré en ce qui concerne la composante alternative du courant d’émetteur (à la fréquence de 467kHz), comme une liaison de résistance négligeable. On en déduit donc que tout se passe, pour la composante alternative, comme si le transistor se trouvait branché directement en parallèle sur le circuit résonnant.

La résistance R qui amortit le circuit résonnant et qui en détermine la bande passante est donc donnée par la mise en parallèle de la résistance d’entrée r_e du transistor suivant (ramenée naturellement au primaire) et par la résistance de sortie r_s du transistor considéré.

Si l’on se rappelle encore que pour avoir un gain maximum en puissance, il faut déterminer le rapport de transformation de telle sorte que la valeur de r_e ramenée au primaire soit égale à r_s, on en déduit alors que la valeur de R est égale à la moitié de r_s. Dans le cas de l’exemple r_s = 29kΩ et R sera donc égale à 29/2 = 14,5kΩ. On doit donc obtenir une bande passante B = 9kHz avec cette valeur de R et pour f_o = 467kHz.

En partant des valeurs ci-dessus, on peut déterminer L et C.

On commence tout d’abord par calculer le coefficient Q du circuit, nécessaire pour obtenir la bande passante désirée :

Q = f_o/B = 467/9 = 51,88 soit 52 environ

On calcule ensuite la valeur de la réactance X_o :

X_o = R/Q = 14,5/52 = 0,279kΩ

Ensuite, on détermine les valeurs de L et C à l’aide des formules suivantes où L est exprimée en mH, C en nF, X_o en kΩ et f_o en kHz.

L = (159 x X_o)/f_o = (159 x 0,279)/467 = 0,095 mH

C = 159/(f_o x X_o ) = 159/(467 x 0,279) = 1,22nF

On peut vérifier rapidement qu’avec de telles valeurs on obtient bien la fréquence de résonnance voulue. En effet :

f_o = 159/√(L x C) = 159/√(0,095 x 1,22) = 159/√0,116 = 159/0,34 = 467kHz

La valeur de C ainsi calculée est celle qui est nécessaire pour que l’inductance L résonne à 467kHz ; en pratique, cependant, on prendra une capacité un peu plus faible pour la raison suivante : en examinant la figure 4, on voit que la capacité de sortie c_s (38pF dans notre exemple) du transistor se trouve en parallèle sur le circuit résonnant pour la même raison que tout à l’heure, où l’on avait vu que la résistance de sortie se trouvait en parallèle sur le C.O. (abréviation de "circuit oscillant").

D’autre part, la capacité d’entrée du transistor suivant, ramenée au primaire se trouve elle aussi en parallèle sur L. Dans le cas de l’exemple, ce = 870pF. Comme le rapport de transformation est 6, la valeur de c'_e ramenée au primaire est :

c'_e  = c_e /n² = 870/6² = 870/36 = 24pF environ

En parallèle sur L, il y a encore la capacité par rapport à la masse des différentes connexions et la capacité répartie du bobinage lui-même, que l’on peut évaluer pour l’ensemble à c_p = 18pF environ.

La capacité parasite totale est donc :

C_t = c_s + c'_e + c_p = 38 + 24 + 18 = 80pF

La capacité à placer sur L devra donc avoir pour valeur :

C’ = C – C_t = 1.220 – 80 = 1140pF (= 1,14nF)

Comme les capacités de sortie et d’entrée peuvent varier d’un transistor à l’autre et que la capacité parasite ne peut être déterminée avec certitude, il est indispensable qu’en pratique on puisse régler la valeur de la capacité ou de l’inductance pour pouvoir accorder exactement le circuit sur la fréquence voulue. On utilise en général une self à noyau réglable, et plus rarement une capacité variable.

Nous étudierons dans la prochaine leçon, le comportement d’un circuit réel.

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 22^ème LEÇON THÉORIQUE

1° - On doit utiliser, au minimum, un générateur basse fréquence (s’il s’agit d’un amplificateur BF), un microampèremètre d’entrée et un voltmètre de sortie.

2° - Pendant le relevé de la courbe de réponse, on doit maintenir constante la valeur du courant d’entrée I_e de l’amplificateur (d’où l’utilité du microampèremètre d’entrée).

3° - La courbe de réponse exprime comment varie l’amplitude du signal de sortie (ou le gain en courant) en fonction de la fréquence).

4° - On appelle fréquences de coupures d’un amplificateur, les deux fréquences (une inférieure, l’autre supérieure) pour lesquelles le gain se réduit à 70,7 % de la valeur qu’il avait pour les fréquences moyennes.

5° - La bande passante d’un amplificateur est définie comme étant la gamme de fréquences comprises entre les fréquences de coupure.

6° - La fréquence de coupure supérieure d’un étage, dépend de la fréquence de coupure propre du transistor utilisé et lui est égale en général.

7° - La fréquence de coupure inférieure d’un étage à liaison par capacité dépend de la valeur de la capacité de liaison et est d’autant plus faible que la valeur de la capacité est plus élevée.

8° - Dans le cas d’un étage à couplage par induction, la fréquence de coupure inférieure dépend de l’inductance du primaire du transformateur et elle est d’autant plus faible que cette inductance est plus grande.

9° - Quand un amplificateur est constitué par plusieurs étages identiques, la bande passante résultante est toujours plus réduite que celle correspondant à un seul étage.

---

EXERCICES DE RÉVISION SUR LA 23^ème LEÇON THÉORIQUE

1° - De quoi dépend la fréquence de résonance d’un circuit ?

2° - A quoi est équivalent un circuit résonnant, constitué d’une capacité, d’une self et d’une résistance en parallèle, pour la fréquence de résonnance ?

3° - Comment doit-être un circuit résonnant pour que sa bande passante soit étroite ?

4° - Quelles sont les valeurs courantes utilisées pour les fréquences intermédiaires dans les récepteurs AM ?

5° - Donner la formule qui permet de calculer la fréquence de résonance f_o en Hertz lorsque la self est exprimée en Henry et la capacité en microfarads ?

6° - Calculer la fréquence de résonance d’un circuit dont la self L = 6,5 mH et la capacité C = 400pF.

7° - Quelle sera la valeur du coefficient de surtension Q lorsque : R = 0,750 MΩ et X_o = 1,5kΩ ?

8° - Calculer la bande passante d’un circuit dont le coefficient Q = 75 et pour lequel la fréquence de résonance est f_o = 100kHz

9° - Si l’on désire que la bande passante du circuit ci-dessus soit trois fois plus grande, que doit-on faire ?

Fin de la leçon 23

---

LECON 24

1-CIRCUITS REELS

Dans les considérations faites jusqu’à présent, on a supposé que l’inductance du circuit ne présentait aucune résistance au passage du courant. Or en fait c’est faux, car la bobine est réalisée à l’aide d’un fil qui a sa propre résistance électrique.

À ce propos il faut signaler que la résistance présentée par un conducteur au passage d’un courant alternatif est toujours plus élevée que la résistance présentée à un courant continu, telle qu’on peut la mesurer avec un ohmmètre.

Ceci est dû à ce que l’on appelle Effet Pelliculaire ou Effet de Peau : le courant alternatif ne se répartit pas de manière uniforme dans toute la section du conducteur comme le fait un courant continu, mais il a tendance à se concentrer à la superficie. De cette manière, la région centrale du conducteur n’est pas parcourue par le courant alternatif, et tout se passe comme si le conducteur n’était composé que de la seule région extérieure (d’où le nom de "peau"). La section utile au passage du courant est donc réduite et sa résistance est ainsi plus élevée que celle offerte au passage d’un courant continu.

"L’effet de peau" dépend de la fréquence du courant (plus celle-ci est élevée plus la section utile du conducteur se réduit) et aussi de la section du conducteur (le phénomène est plus accentué dans les fils de grosse section que les fils petits).

Tandis que pour les fréquences BF cet effet est pratiquement négligeable, il devient prépondérant en HF et il faut absolument en tenir compte, car la résistance devient 10 fois plus grande (ou même plus) que celle mesurée en courant continu.

Pour donner une idée plus précise de l’accroissement de la résistance d’un conducteur lorsque la fréquence augmente, je vous ai reporté à la figure 1 différentes courbes relatives à des conducteurs de section différente.

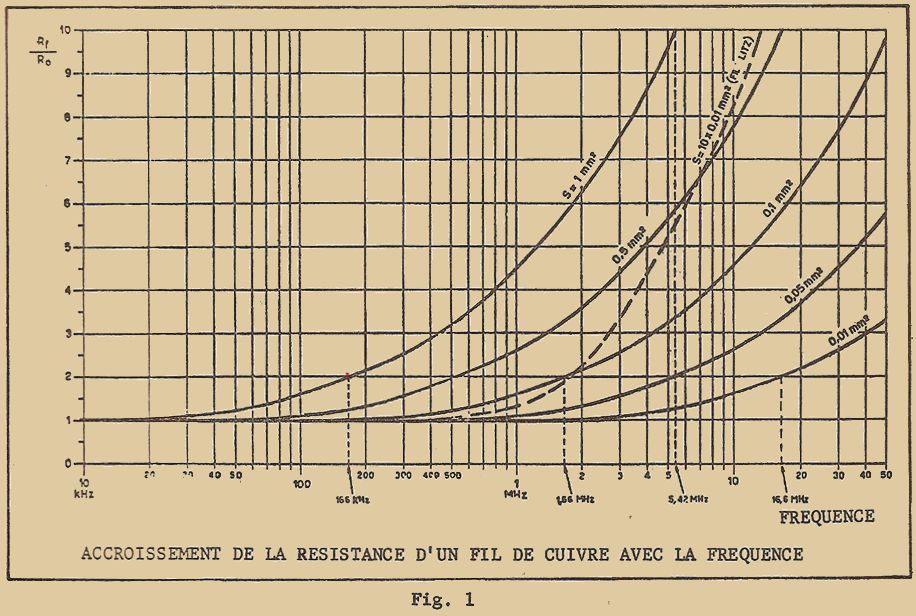
Considérons par exemple un conducteur en cuivre de section S = 1mm². Sur la courbe.S = 1mm² de la figure 1, nous voyons que pour f = 166kHz, R_f/R_o = 2. Ceci signifie qu’à la fréquence 166kHz, la résistance R_f du conducteur considéré est deux fois plus grande que la résistance R_o en courant continu.

Si l’on augmente la fréquence, le rapport R_f / R_o croît. Ainsi à 5,42MHz il est égal à 10. Ceci signifie donc, qu’à cette fréquence la résistance R_f est dix fois plus grande qu’en courant continu.

Ainsi, un conducteur de 1mm² de section et de 1 m de long a une résistance R₀ = 17,8mΩ en courant continu. A la fréquence 166kHz, la résistance a doublé et est devenue R_f = 35,6mΩ et à 5,42MHz, elle est de 178mΩ.

Si l’on examine par contre un conducteur ayant une section de 0,1mm² (courbe repérée 0,1mm²) on voit que sa résistance reste pratiquement constante jusqu’à 166kHz environ. Pour des fréquences plus élevées, vers 1,66MHz sa valeur a doublé. Par contre, pour un conducteur de section 0,01mm², la valeur de sa résistance ne double que lorsque la fréquence atteint 16,6MHz.

On en conclut donc que plus la section est faible plus on peut "monter" en fréquence avant que la résistance ne double. De cette constatation est née l’idée d’utiliser, pour les fréquences élevées, des conducteurs formés de plusieurs fils fins au lieu de prendre du fil de forte section. Par exemple, au lieu d’utiliser un conducteur de section 0,1mm² formé par un seul fil, il est préférable de prendre un conducteur formé de 10 fils ayant chacun une section de 0,01mm².

L’avantage que l’on peut obtenir avec un tel conducteur est clairement représenté sur la figure 1. La courbe en trait plein (S = 0,1mm²) se trouve au-dessus de la courbe en traits pointillés (S = 10 x 0,01mm²) correspondant au fil de litz jusque vers 2MHz environ. Ceci signifie donc que pour des fréquences inférieures à 2MHz, le fil de litz est préférable au fil à un seul conducteur (de section totale équivalente). Par contre au-dessus de 2MHz l’aug_mentation de la résistance dûe au fil de litz est plus rapide que pour un fil à un seul conducteur. C’est pour cette raison que dans les récepteurs on utilise surtout du fil de litz pour les bobines grandes ondes et petites ondes ainsi que pour les transformateurs F.I. (fréquences inférieures à 2MHz) et que l’on utilise de nouveau du fil plein pour des bobines ondes courtes (fréquences supérieures à 2MHz).

Si l’on veut tenir compte de la résistance de la bobine utilisée pour le C.O. (circuit oscillant), on peut procéder de la même manière que lors de l’étude de l’étage de puissance avec transformateur de sortie. On suppose que la bobine réelle est équivalente à une bobine idéale (c’est-à-dire sans résistance) qu’elle a même inductance que la bobine réelle et qu’en série il y a une résistance R_f, de valeur égale à la résistance qu’elle a à la fréquence de travail.

Ainsi le circuit résonnant réel de la figure 2a, peut être considéré comme étant équivalent au circuit de la figure 2b, où la bobine est idéale, mais où il y a en série une résistance R_f.

Reprenons l’exemple du C.O. de la figure 4 (Théorie 23), où C = 1,22nF et L = 0,095mH. Supposons qu’à la fréquence de travail (467kHz) la résistance R_f = 2Ω (valeur qui correspond à celle mesurée en courant continu, par exemple à l’aide d’un ohmmètre, aug_mentée dans le rapport R_f / R_o d’après le graphique de la figure 1).

On démontre qu’un circuit résonnant du type de la figure 2b, (c’est-à-dire du type série, en ce sens que la self et la résistance sont en série), a un coefficient de surtension Q :

Q = X_o/R_f

où X_o est la réactance de la self à la fréquence de résonance, qui doit être exprimée dans les mêmes unités que R_f.

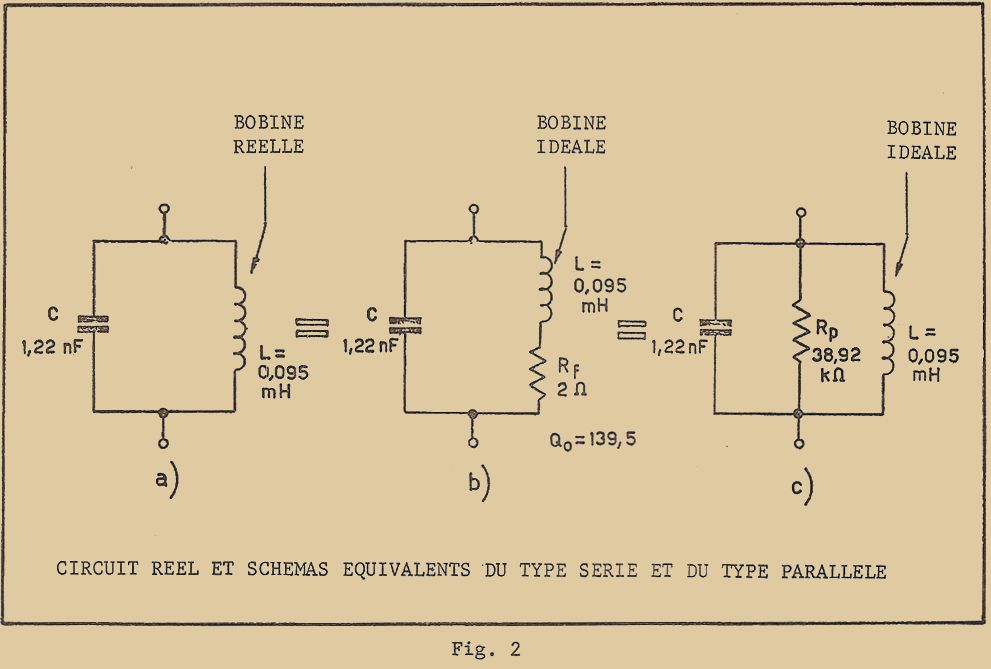
Dans l’exemple nous avons X_o = 0,279kΩ et R_f = 2Ω. D’où :

Q = 279/2 = 139,5

Le circuit réel de la figure 2a sera donc caractérisé, non seulement par une valeur de capacité et de self, mais aussi par une valeur de Q_o déterminée par la résistance de la bobine. Le coefficient de qualité est d’autant plus élevé que la résistance R_f est plus faible.

La même valeur de Q_o peut être obtenue en prenant un circuit idéal et en l’amortissant avec une résistance R_p placée en parallèle à ses bornes comme l’indique la figure 2c. On démontre alors que la valeur de R_p doit être Q_o fois la valeur de R_f.

Dans le cas considéré, R_p devra avoir comme valeur :

R_p = Q_o² x R_f = (139,5)² x 2 = 19.460,25 x 2 = 38.920,50Ω soit environ 38,92kΩ.

En effet, si l’on reprend la formule vue précédemment, à propos du circuit de la figure 2 (Théorie 23), on trouve :

Q = R/X_o = 38,92/0,279 = 139,5

On peut donc en conclure qu’un circuit résonnant réalisé avec une bobine réelle se comporte de la même manière qu’un circuit résonnant idéal amorti par une résistance R_p placée en parallèle sur le circuit même. Cet amortissement est d’autant plus fort (c’est-à-dire que R_p est faible) que R_f est élevée. En d’autres termes, nous dirons, que l’amortissement est d’autant plus fort que le coefficient de surtension du circuit est plus faible.

Dans tous les exemples vus jusqu’à maintenant, où l’on considérait des C.O. idéaux, on tient compte en pratique de ce que ces circuits ne le sont pas, en considérant qu’en parallèle sur la résistance d’amortissement R vient se placer la résistance R_p que l’on vient de voir, ce qui accroît encore l’amortissement du C.O. (Circuit Oscillant).

1 – 1 GAIN EN PUISSANCE – NEUTRODYNAGE

Dans les amplificateurs HF ou FI tels que ceux de la figure 4 (Théorie 23), il n’y a pas que le gain en courant ou en tension qui soit intéressant, il y a aussi le gain en puissance. Connaissant les valeurs de la transconductance, des résistances d’entrée et de sortie, le gain en puissance est donné par la formule suivante :

Gp = (g_m² x r_e x r_s)/4

où r_e et r_s doivent être exprimés en kΩ si la transconductance g_m est donné en mA/V

Si g_m = 35 mA/V, r_e = 0,8 kΩ et r_s = 29 kΩ, le gain en puissance sera :

Gp = (35² x 0,8 x 29)/4 = (1225 x 0,8 x 29)/4 = 28.420/4 = 7.105

Il faut encore remarquer que le gain calculé ci-dessus est le gain maximum théorique, valable dans le cas idéal où la self est sans résistance.

En pratique, à cause de la résistance de la bobine, on ne peut obtenir un gain de puissance aussi élevé, mais on pourra s’en rapprocher d’autant plus que le Q_o du C.O. sera plus élevé.

Une autre raison fait qu’en pratique le gain en puissance est inférieur à celui calculé : c’est la présence de la capacité de la jonction collecteur-base. Pour mettre en évidence cette capacité, on a dessiné en pointillés sur la figure 3 un condensateur C_CB placé entre collecteur et base. On remarque immédiatement qu’au travers de C_CB une partie du signal (bien que faible) retourne de la sortie du transistor (collecteur) à l’entrée (base) en se superposant au signal de commande. En raisonnant en courants on dira qu’au courant de commande i_e vient se superposer le courant i_r qui provient du collecteur et se dirige vers la base à travers C_CB.

Le courant de base résultant est en général plus faible que le courant de commande, car i_e et i_r sont souvent en opposition de phase ; mais il peut arriver aussi que les deux courants soient en phase, auquel cas, le courant de base est plus grand que le courant de commande.

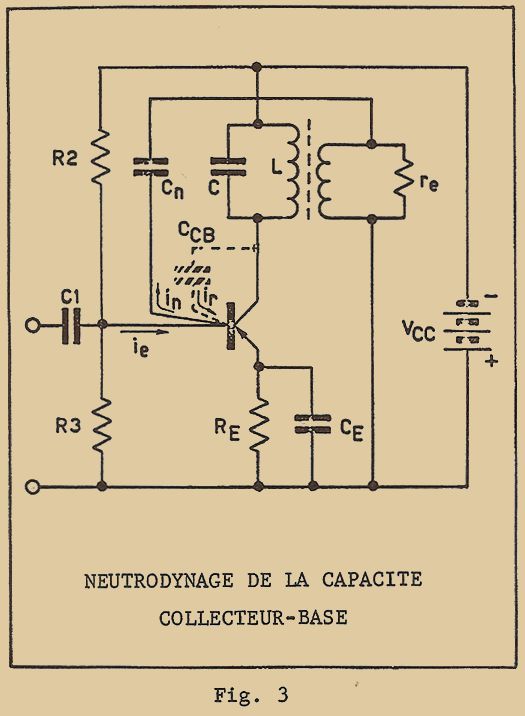
Dans le premier cas, la puissance de sortie sera plus faible que s’il n’y avait pas de capacité C_CB ; dans le second cas au contraire, elle sera plus grande et si i_r est suffisamment élevé, on peut avoir un accrochage et l’étage ne pourra plus fonctionner comme amplificateur.

Afin d’éviter de tels inconvénients, provoqués par la présence de C_CB, il ne reste plus qu’à neutraliser les effets dûs à i_r en faisant parvenir à la base un second courant in de phase opposée à celle de i_r. Ceci s’obtient en pratique en branchant un condensateur de neutrodynage C_n entre la base et le secondaire du transformateur.

Si dans le secondaire du transformateur circule un courant en opposition de phase par rapport au courant du primaire, il est évident que le courant in sera lui aussi en opposition de phase avec i_r ; en réglant convenablement la valeur de C_n, on fera en sorte que les deux courants se neutralisent mutuellement et on évitera ainsi les inconvénients décrits ci-dessus.

Il faut encore remarquer que le neutrodynage est nécessaire avec les transistors alliés car dans ceux-ci, la capacité C_CB est de l’ordre d’une dizaine de pF et que son effet est très sensible. Dans les transistors à diffusion ("drift") la capacité C_CB est notablement plus faible, et dans la plupart des cas il n’est pas nécessaire de recourir au neutrodynage.

1 – 2 LIAISON PAR TRANSFORMATEUR A PRIMAIRE ET SECONDAIRE ACCORDÉS

Un autre type de transformateur est utilisé dans la liaison entre étages F.I. Dans ces transformateurs, le primaire et le secondaire sont simultanément accordés sur la fréquence de travail. Le schéma de l’étage amplificateur se présente alors comme sur la figure 4 où l’on peut voir clairement que le primaire est constitué par un C.O. formé de L_p et de C_p et que le secondaire est constitué lui aussi par un C.O. formé de L_s et de C_s, tous les deux accordés sur la même fréquence.

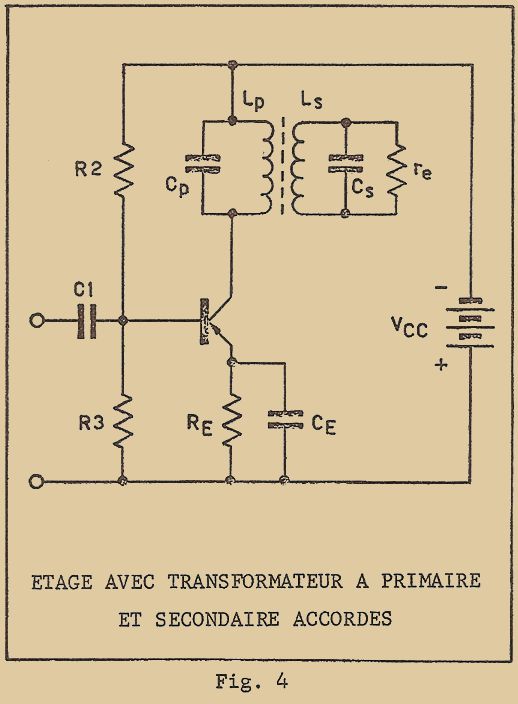
Avant de commencer l’étude du circuit de la figure 5, il est bon de décrire rapidement comment se présentent en pratique de tels transformateurs et quelles différences il y a par rapport au transformateur des schémas précédents.

Le transformateur comme celui de la figure 4 (Théorique 23), est réalisé sur un support isolant de forme cylindrique. Sur l’enroulement primaire, est enroulé directement l’enroulement secondaire comme le montre la figure 5. A l’intérieur du support se visse un noyau ferromagnétique qui en pénétrant plus ou moins permet d’accorder la self exactement sur la fréquence désirée.

Le transformateur du schéma de la figure 4 est au contraire constitué de 2 enroulements réalisés sur le même support cylindrique, mais complètement séparés l’un de l’autre (figure 5b). Le réglage de la fréquence de résonance des deux circuits accordés est réalisé maintenant à l’aide de deux noyaux l’un placé en haut (primaire) et l’autre en bas (secondaire).

Les deux transformateurs sont accordés à l’aide des capacités et enfermés dans un boitier métallique relié à la masse.

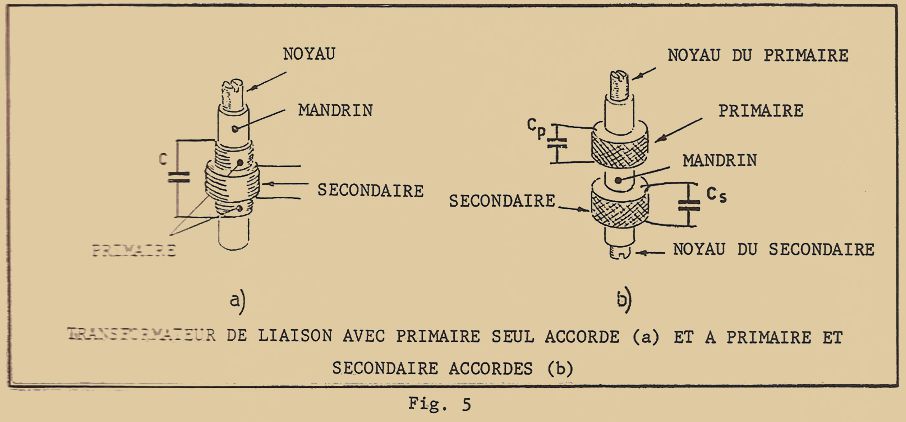
Après cette brève parenthèse d’ordre technologique, nous pouvons commencer l’étude du fonctionnement du circuit de la figure 4 dont la particularité essentielle réside dans la forme de la courbe de résonance et donc dans l’aptitude de l’étage à sélectionner le signal à la fréquence désirée parmi toutes les fréquences reçues. La détermination de la courbe de résonance est faite de la même manière que celle de la figure 2 (Théorique 23) relative à un seul circuit. Il suffit pour cela de faire circuler dans le primaire un courant de valeur constante et de fréquence variable, de se placer autour de la fréquence de résonance sur laquelle sont accordés primaire et secondaire et de mesurer la valeur de la tension aux bornes du secondaire comme le montre la figure 6.

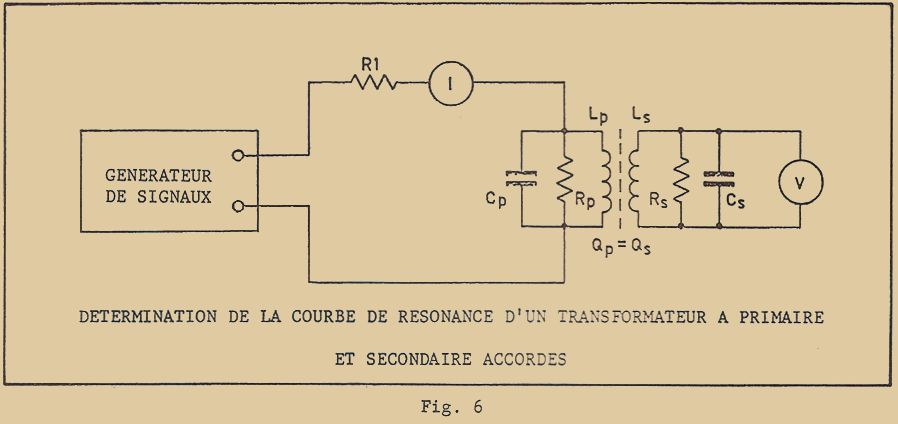
Si l’on suppose que le primaire et le secondaire sont respectivement amortis par R_p et R_s de façon à ce que les deux circuits aient la même valeur de coefficient de surtension Q, on trouve des courbes différentes selon le couplage qui existe entre les deux bobines, c’est-à-dire selon la distance entre les deux bobines de la figure 5b.

Si les deux bobines sont très éloignées, la courbe obtenue est assez semblable à celle de la figure 2 (Théorique 23) ; lorsque l’on rapproche les deux bobines (c’est-à-dire lorsque l’on augmente leur couplage) la tension au secondaire augmente ; on trouve d’autre part que la courbe devient de plus en plus large au fur et à mesure que l’on augmente le couplage (c’est-à-dire que l’on rapproche les bobines).

En rapprochant encore les deux bobines, on trouve qu’à un certain moment l’amplitude de la courbe ne croît plus (figure 7) et que le maximum de la tension n’a plus lieu pour la fréquence de résonance f_o mais pour deux fréquences équidistantes, l’une supérieure l’autre inférieure à la fréquence de résonance.

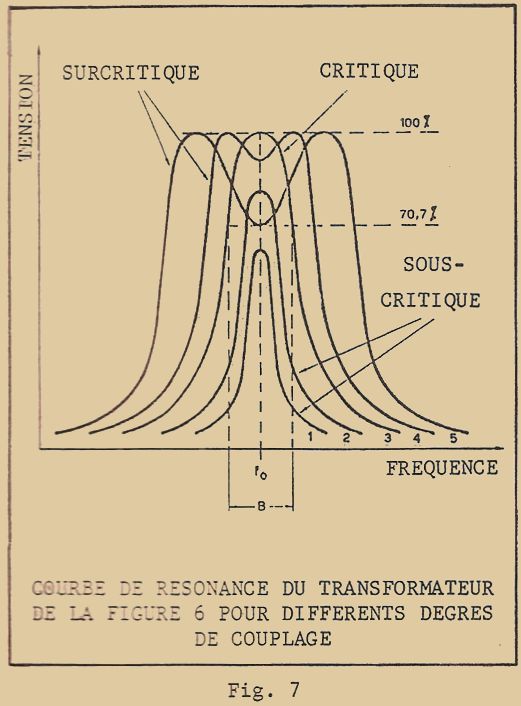
On définit le couplage critique comme étant celui pour lequel on obtient la tension maximum possible au secondaire à la fréquence de résonance (courbe 3 de la figure 7).

On dit que le couplage est sous-critique lorsque la tension au secondaire est inférieure à la valeur maximum possible (courbes 1 et 2). On dit que le couplage est sur-critique lorsque la tension au secondaire atteint la valeur maximum, pas à la fréquence de résonance, mais pour deux fréquences différentes de celle-ci, c’est-à-dire lorsque la courbe présente deux bosses et un creux à la fréquence de résonance (courbes 4 et 5).

Dans les transformateurs utilisés en pratique, on choisit le couplage critique ou un peu supérieur à celui-ci, de façon à ce que le creux ne soit pas trop prononcé. De cette façon on a l’avantage d’obtenir le maximum de gain possible (un couplage inférieur au couplage critique donne en effet une tension plus faible à la résonance) et une bande passante qui est environ une fois et demi celle d’un circuit accordé simple ayant le même coefficient Q (un couplage supérieur au couplage critique donnerait une bande passante encore plus grande, mais présenterait l’inconvénient du creux).

Dans le cas de l’étage de la figure 4, le transformateur sera réalisé de façon à ce que le couplage soit critique en plaçant de façon appropriée les deux bobines sur le support cylindrique. Dans ces conditions, le rapport entre les spires du primaire et du secondaire, c’est-à-dire n, sera encore donné par la formule n = √(r_s⁄r_e) comme dans le cas de la figure 4 (Théorique 23).

Pour obtenir encore une bande passante B = 9kHz comme auparavant, les valeurs de Qp du primaire et de Qs du secondaire devront être toutes les deux égales et seront données par la formule :

Q = (f_o x 1,41)/B = (467 x 1,41)/9 = 658,47/9 = 73,16

En indiquant par X_op et X_os les réactances à la résonance du primaire et du secondaire, on trouve : (avec r_s = 29kΩ et r_e = 0,8kΩ)

X_op = r_s/Q = 29/73,16 = 0,396kΩ

X_os = r_e/Q = 0,8/73,16 = 0,0109kΩ

Les formules ci-dessus dérivent du fait que dans le cas de la figure 4, le primaire n’est amorti que par la résistance de sortie r_s du transistor, tandis que le secondaire n’est amorti que par la résistance d’entrée r_e du transistor de l’étage suivant.

Les valeurs des selfs, des capacités primaires et secondaires, indiquées par L_p , C_p, L_s et C_s sont données, comme dans le cas du schéma de la figure 4 par les formules suivantes :

L_p = (159 x X_op)/f_o = (159 x 0,396)/467 = 0,1348 mH

C_p = 159/(f_o x X_op ) = 159/(467 x 0,396) = 0,859nF

L_s = (159 x X_os)/f_o = (159 x 0,0109)/467 = 0,0037mH

C_s = 159/(f_o x X_os ) = 159/(467 x 0,0109) = 3,12nF

Naturellement il faudra prendre des capacités C’_p = C_p – C_s = 859 – 38 = 821 pF et C’_s = C_s – C_e = 3120 – 870 = 2250pF afin de tenir compte des capacités des transistors.

Pour comparer directement les avantages obtenus avec le circuit de la figure 4 par rapport à celui de la figure 4 (Théorique 23), je vous ai reporté à la figure 8, les courbes de sélectivité calculées pour ces deux circuits.

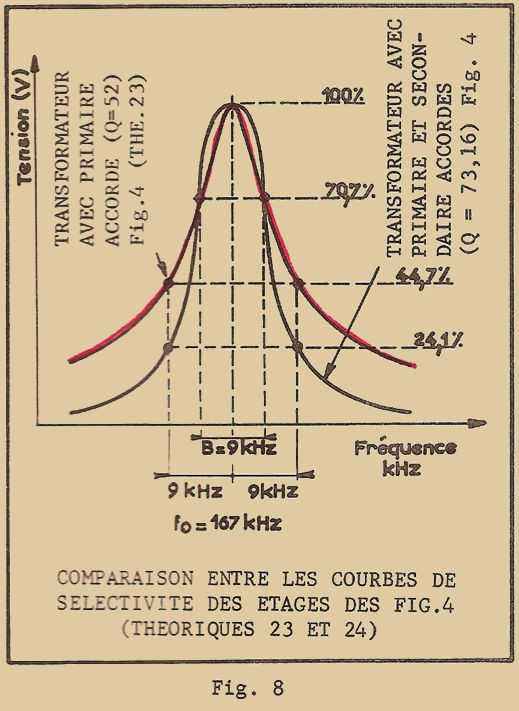
Comme vous pouvez le voir, les bandes passantes sont égales dans les deux cas, mais la courbe correspondant au cas du transformateur à primaire et secondaire accordés est plus intéressante car elle possède des flancs plus raides, ce qui indique qu’elle est plus apte à atténuer les fréquences en dehors de la bande passante.

Ainsi par exemple, si l’on prend la fréquence de 9kHz au-dessus et en dessous de fo (ce qui représente les porteuses des stations adjacentes à celle reçue), on voit que pour le circuit de la figure 4, elle sera plus atténuée à la sortie de l’amplificateur (24,1 %) que dans le cas du circuit de la figure 4 (Théorique 23) (44,7 %).

D’autre part, dans la bande passante, la courbe relative à l’étage de la figure 4 est plus "rectangulaire". Ceci indique que le circuit amplifie beaucoup plus uniformément les signaux dans la bande passante.

En conclusion, le circuit de la figure 4 est de beaucoup préférable à celui de la figure 4 (Théorique 23). C’est pour cela qu’il est surtout utilisé.

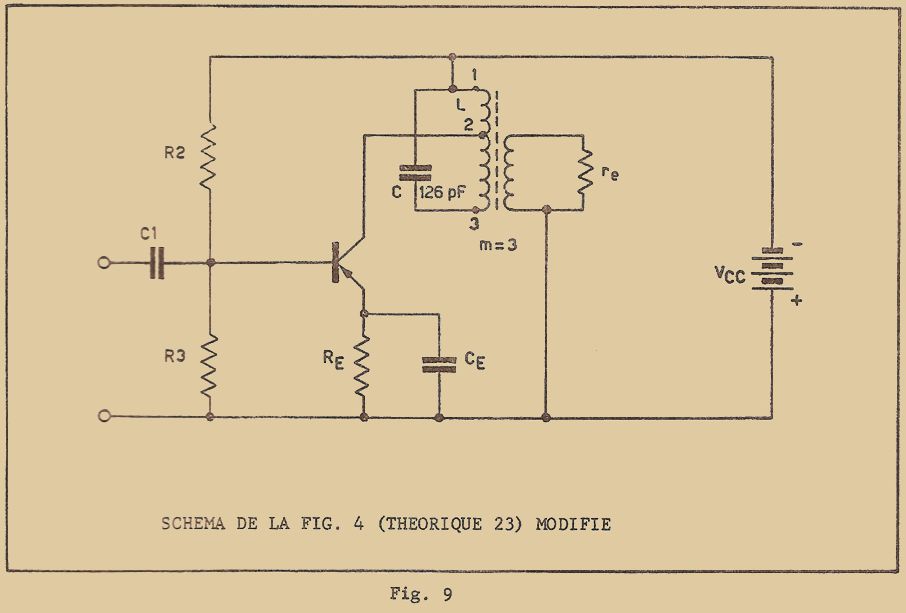
1 – 3 TRANSFORMATEURS À PRISE INTERMEDIAIRE

Comme on l’a vu avec les calculs ci-dessus, les valeurs des capacités utilisées dans les circuits accordés sont relativement élevées et en général on ne peut les placer à l’intérieur des blindages renfermant le transformateur F.I.

Pour réduire la valeur de la capacité (et d’autre part pour permettre d’utiliser des capacités de même valeur au primaire et au secondaire dans le cas d’un circuit du type de la figure 4) on utilise l’artifice de prolonger les enroulements et de brancher les condensateurs aux extrémités de ceux-ci comme le montre la figure 9 (schéma de la figure 4 Théorique 23 modifié).

Comme on le voit sur la figure, le condensateur d’accord C est branché non plus entre collecteur (point 2) et l’alimentation du collecteur (point 1) mais entre le point 1 et le point 3 qui représente l’extrémité du prolongement du bobinage.

On démontre alors que si l’on indique par m le rapport entre le nombre total de spires comprises entre 1 et 3 et le nombre de celles-ci comprises entre 1 et 2 (et qui sont nécessaires pour réaliser la valeur de la self calculée auparavant) la valeur de C de la capacité à brancher entre les points 1 et 3 est donnée par la formule :

C = C'/m²

Supposons que nous prolongions l’enroulement de façon à ce que le nombre total de spires soit 3 fois celui compris entre 1 et 2 (m = 3) ; la valeur de la capacité va se réduire de la valeur C’ = 1140 pF à :

C = 1140/(3)² = 1140/9 = 126pF environ

Si l’on voulait réduire la capacité de 1140pF à 220pF (valeur normalisée pour les condensateurs mica et au polystyrène) le rapport m devrait avoir pour valeur :

m = √(1140/220) = √5,18 = 2,27 environ

Ce qui vient d’être dit, en ce qui concerne la figure 9, reste évidemment valable pour les circuits de la figure 4, où l’on obtient comme avantage, la possibilité d’utiliser les mêmes valeurs des capacités d’accord pour le primaire et le secondaire.

---

EXERCICES DE RÉVISION SUR LA 24^ème LEÇON THÉORIQUE

1 – Quel est le coefficient de surtension d’un circuit dans lequel X_o = 0,300 kΩ et où R_f = 5Ω

2 – Quelle est alors la valeur équivalente de la résistance R_p ?

3 – Comment peut-on exprimer R_p en fonction de R_f, de la self L et de la pulsation de résonance ω ?

On rappelle que ωo = 2πfo

4 – A l’aide de la formule calculée ci-dessus, déterminer la valeur de R_p sachant que L = 2 henrys :

f_o = 300Hz et R_f = 100Ω

5 – Qu’appelle- t-on "effet de peau" ou "effet pelliculaire" ?

6 - Comment est constitué un fil de litz et quels sont ses avantages par rapport à un conducteur normal ?

7 – Quelles sont les différences technologiques entre un transformateur constitué par un seul primaire accordé et un dont le secondaire est aussi accordé ?

8 – Qu’appelle-t-on couplage critique ?

9 – Quel aspect présente la courbe de résonance quand le couplage est supérieur au couplage critique ?

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 23^ème LEÇON THÉORIQUE

1 – La fréquence de résonance d’un circuit dépend uniquement des valeurs de l’inductance et de la capacité qui le constituent.

2 – Un circuit résonnant formé d’une capacité, d’une inductance et d’une résistance en parallèle est équivalent, à la fréquence de résonance, à sa seule résistance.

3 – Pour que la bande passante d’un circuit résonnant soit étroite, il faut que ce dernier soit peu amorti, c’est-à-dire que sa résistance en parallèle doit être de valeur très élevée.

4 – Dans les récepteurs AM, les fréquences intermédiaires sont en général de 467kHz, 480kHz ou 455kHz.

5 – La fréquence de résonance f_o est :

f_o = 159/√(L x C)

6 – f_o = 100kHz environ

7 – R = 0,750 MΩ = 750 kΩ

d’où Q = 750/1,5 = 500

8 – B = f_o/Q = 100/75 = 1,33kHz

9 – Pour augmenter la bande passante de trois, il faut diminuer le coefficient de qualité de trois, c’est-à-dire amortir le circuit.

On veut B = 1,33 x 3 = 4 environ

Le coefficient Q doit donc être

Q = f_o/B = 100/4 = 25 (= 75/3 )

Fin de la leçon 24

---

LECON 25

1 – OSCILLATEURS SINUSOÏDAUX

Tous les circuits à transistors étudiés jusqu’à maintenant, présentaient une propriété commune qui était de délivrer à la sortie un signal, d’une certaine puissance (plus ou moins grande selon le type de transistor utilisé) quand on appliquait à l’entrée, et seulement à ce moment-là, un signal de commande.

Le nom d’Amplificateur donné à ces circuits provient du fait qu’ils sont capables, si on leur applique à l’entrée un certain signal, de délivrer à leur sortie un signal de puissance plus grande, et plus ou moins fidèle d’ailleurs.

Par contre, il faut noter que les amplificateurs ne délivrent aucun signal à leur sortie si aucun signal n’est appliqué à leur entrée.

Nous allons voir aujourd’hui d’autres circuits, capables eux de délivrer un signal à leurs bornes de sortie, même si aucun signal n’était appliqué à leur entrée. Ces circuits sont appelés OSCILLATEURS en ce sens qu’ils peuvent produire des oscillations par eux-mêmes. Le signal de sortie pourra être simple lorsqu’il s’agira d’un signal sinusoïdal. Il pourra être aussi beaucoup plus complexe, comme dans le cas d’ondes rectangulaires ; mais de toute façon, ces signaux sont périodiques car ils se répètent avec une certaine période.

Nous étudierons les Oscillateurs Sinusoïdaux. Par contre, les Oscillateurs non sinusoïdaux ne seront pas pris en considération car ils ne sont jamais utilisés dans les récepteurs radio.

Comme les amplificateurs, les oscillateurs peuvent être classés selon les caractéristiques du signal délivré ou selon celles du circuit utilisé.

Comme nous l’avons v_u en son temps, une onde sinusoïdale peut être déterminée par sa fréquence et par son amplitude. Les oscillateurs pourront être classés selon la fréquence du signal produit et selon l’amplitude de celui-ci ou mieux, selon la puissance du signal, puisque cette dernière dépend directement de l’amplitude du signal.

Les fréquences qui intéressent les récepteurs, peuvent être divisées en deux bandes : la bande BF (ou de fréquences acoustiques) comprise entre 20Hz et 20kHz (sons audibles par l’oreille humaine) et la bande des Radio-fréquences, qui s’étend de quelques dizaines dekHz à quelques dizaines deMHz, comprenant la gamme utilisée pour les transmissions en modulation d’amplitude, c’est-à-dire grandes ondes (GO), les petites ondes ou moyennes (PO) et les ondes courtes (OC).

Les oscillateurs pourront être : du type BF ou du type HF.

Les oscillateurs du premier type produisent des signaux sinusoïdaux de fréquence acoustique et d’amplitude constante (figure 1a).

De tels signaux amplifiés par des amplificateurs BF donneront dans le haut-parleur, un son acoustique de tonalité fixe (d’une seule fréquence).

Les oscillateurs BF peuvent encore être subdivisés en oscillateurs à une seule fréquence fixe ou à plusieurs fréquences fixes selon qu’ils peuvent délivrer une ou plusieurs fréquences prédéterminées et en oscillateurs à fréquence variable s’ils peuvent couvrir toute, ou une partie de la gamme acoustique.

On peut de la même manière, subdiviser les oscillateurs HF. Ceux-ci pourront aussi être catalogués en outre en oscillateurs non modulés s’ils délivrent une onde sinusoïdale (HF bien entendu) d’amplitude constante (figure 1b) c’est-à-dire non modulée, et en oscillateurs modulés quand l’amplitude de l’onde varie périodiquement selon une forme encore sinusoïdale mais de fréquence acoustique (figure 1c).

Ce dernier type de signal, appliqué à l’antenne d’un récepteur, donnera encore une note acoustique dans le haut-parleur du récepteur.

Les oscillateurs HF sont indispensables pour le réglage et la mise au point des circuits HF et FI des récepteurs.

Suivant le type du circuit utilisé, les oscillateurs peuvent être classés en deux catégories différentes : les oscillateurs à inductance et capacité (oscillateurs LC) lorsque la fréquence du signal est déterminée par la fréquence de résonance d’un circuit résonnant formé par une self et une capacité, les oscillateurs à résistance et capacité (oscillateurs RC), lorsque la fréquence du signal est déterminée par les caractéristiques d’un réseau composé de plusieurs résistances et capacités.

Disons tout de suite, pour fixer les idées, que les oscillateurs HF sont en grande majorité du type à inductance et capacité ; étant donné les valeurs élevées de la fréquence et les faibles valeurs des selfs, ces dernières sont en général bobinées sur des mandrins en matériaux adaptés à la HF ou tout simplement "en l’air".

Les oscillateurs BF peuvent être du type LC ou RC. Dans le premier cas, étant donné les faibles valeurs de la fréquence et les valeurs élevées de l’inductance, les selfs seront réalisées sur des mandrins avec noyaux de ferrite ou des tôles.

Les valeurs élevées nécessaires pour les capacités ne permettent pas l’utilisation de condensateurs variables ; ainsi les circuits LC sont surtout utilisés dans le cas d’oscillateurs à fréquence fixe.

Lorsque l’on a besoin d’oscillateurs à fréquence variable, on préfère utiliser le type RC où les capacités nécessaires sont de faible valeur (donc on peut employer des condensateurs variables) et les résistances en général de fortes valeurs (mais ceci n’est pas un inconvénient, ni du point de vue Technologique ni du point de vue économique).

Une classification ultérieure des oscillateurs LC et RC sera faite en se basant sur le nombre de transistors utilisés et le montage adopté (en général en base commune ou en émetteur commun) A ce propos, disons tout de suite que pour les oscillateurs LC on peut utiliser l’un des deux montages au choix, tandis que pour les oscillateurs RC on n’utilise que le montage en émetteur commun.

Nous allons voir maintenant comment fonctionnent les oscillateurs et en particulier les oscillateurs LC, puisque c’est le type le plus généralisé et qu’en faisant varier les valeurs des composants (inductance et capacité), on peut couvrir soit la gamme acoustique, soit la gamme HF.

Je vous rappelle que le terme d’oscillateur est synonyme de générateur ; on peut donc parler indifféremment d’oscillateurs BF et HF ou de générateurs BF et HF. Ceci n’est pas valable, par contre avec la terminologie américaine, pour laquelle oscillateur> signifie oscillateur BF ou HF non modulé, tandis que générateur, signifie seulement les oscillateurs HF en général et modulés en particulier.

2 – PRINCIPE DE FONCTIONNEMENT D’UN OSCILLATEUR SINUSOÏDAL

Pour étudier le fonctionnement d’un oscillateur sinusoïdal, il convient de partir du schéma d’un amplificateur sélectif, c’est-à-dire dans lequel la charge est constituée par un circuit LC résonnant à la fréquence f_o (voir leçon précédente). Le schéma de cet amplificateur devra toutefois être modifié comme indiqué en figure 2 et, pour le moment, les inverseurs D₁ (dans le circuit de la base) et D₂ (dans le circuit de sortie du secondaire) se trouvent tous les deux sur la position 1.

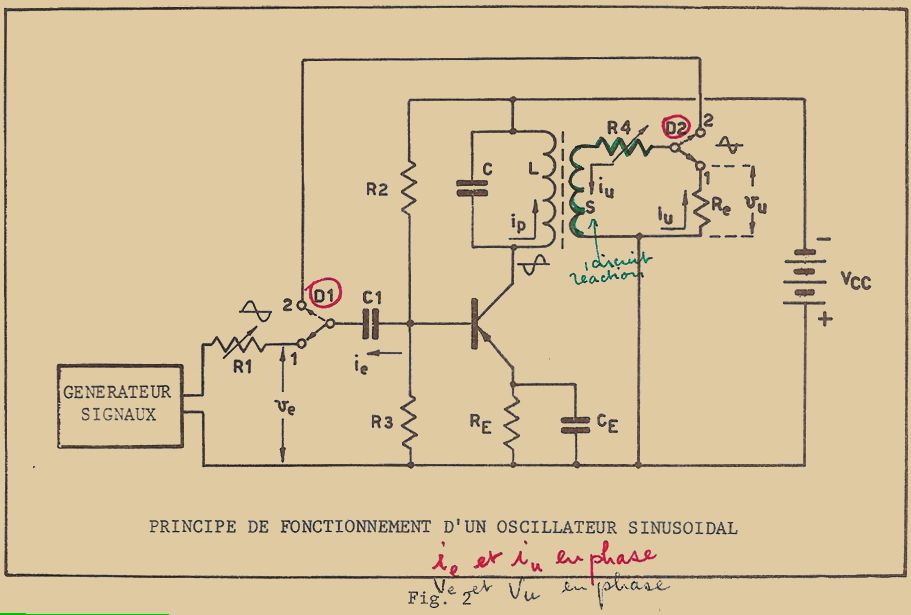
Dans ces conditions, l’entrée de l’amplificateur est reliée au générateur qui est supposé délivrer un signal sinusoïdal de même fréquence que celle sur laquelle est accordé le circuit LC. Le secondaire du circuit résonnant est relié (par l’intermédiaire de la résistance réglable R₄) aux bornes de la résistance de charge R_e dont la valeur est exactement celle de la résistance d’entrée de ce même étage amplificateur (nous verrons bientôt pourquoi ce choix de R_e).

En réglant la résistance variable R₁, on peut régler le courant de commande de l’amplificateur ie, qui pendant l’alternance négative du signal délivré par le générateur circulera dans le circuit de base selon la direction de la flèche ; entre la base et la masse apparaîtra la tension d’entrée v_e.

On peut régler maintenant la résistance R₄ de façon qu’il circule dans la résistance de charge R_e un courant i_u de même intensité que le courant de commande i_e. Ainsi la tension v_u qui va apparaître aux bornes de R_e sera égale à la tension de commande v_e puisque l’on a supposé que R_e avait précisément la valeur de la résistance d’entrée de l’étage.

Il faut remarquer encore, que le courant i_u qui circule dans R_e a le même sens que le courant ie dans le circuit de base (voir flèches figure 2) : les deux courants i_u et ie sont donc en phase.

De même les tensions v_u et v_e sont elles aussi en phase : en effet, une première inversion de phase a lieu dans le transistor et une seconde est opérée à l’aide du transformateur de sorti_e : ainsi la tension aux bornes de la charge se retrouve en phase avec la tension appliquée à l’entrée de l’amplificateur.

Les phases des tensions sont indiquées d’une façon schématique à la figure 2 par des sinusoïdes qui partent vers le haut ou vers le bas ; on peut voir ainsi qu’à l’entrée et à la sortie les sinusoïdes partent toutes les deux vers le haut (c’est-à-dire qu’elles sont en phase), tandis que sur le collecteur, la sinusoïde part vers le bas (c’est-à-dire qu’elle est en opposition de phase avec les deux autres).

En conclusion, grâce à la modification apportée du circuit de l’amplificateur sélectif, il est possible d’obtenir aux bornes de la résistance de charge R_e un signal identique en amplitude et en phase à celui qui est appliqué à l’entrée de l’amplificateur.

En considérant le gain de l’amplificateur, c’est-à-dire le rapport entre la tension de sorti_e et la tension d’entrée (v_u/v_e) comme v_u = v_e, on en déduit que le gain en tension est égal à 1 ; de même, les gains en courant et en puissance sont égaux à 1 (puisque i_u = i_e).

Supposons maintenant que l’on bascule rapidement et simultanément les inverseurs D₁ et D₂ de la position 1 à la position 2. On va s’apercevoir que le circuit "ne se soucie" nullement de cette commutation et qu’il continue à délivrer, par exemple sur le collecteur, le même signal qu’il fournissait lorsque les commutateurs étaient sur la position 1.

En effet, en regardant de plus près le schéma de la figure 2, on peut voir que le circuit de sortie est toujours fermé sur une résistance de même valeur, puisque en passant de la position 1 à la position 2, on remplace la résistance R_e par la résistance d’entrée de l’étage qui a même valeur rappelons-le.

En ce qui concerne le circuit d’entrée, celui-ci est relié, non plus au générateur de signaux, mais à la sortie de l’étage. Etant donné que le signal à la sortie de l’étage était identique en amplitude et en phase à celui qui était présent à l’entrée, le transistor continue à être commandé encore par le même signal.

En d’autres termes, on peut dire que le transistor n’est pas capable de distinguer si le signal de commande lui parvient du générateur ou de son propre circuit de sortie et il ne se "soucie" donc pas si c’est le générateur qui le commande ou bien si c’est lui-même qui s’"auto-pilote".

Ainsi donc, on continue à obtenir un signal à la sortie de l’étage sans rien injecter à l’entrée.

La différence entre le circuit amplificateur et le circuit oscillateur réside dans l’adjonction d’un réseau de réaction qui sert à prélever une fraction du signal de sortie et à le reporter à l’entrée de l’étage de façon à ce qu’il puisse "s’auto-piloter", c’est-à-dire qu’il puisse se maintenir en oscillation.

Le réseau de réaction doit présenter deux propriétés fondamentales pour que le circuit amplificateur puisse se transformer en oscillateur.

Tout d’abord, il doit inverser la phase du signal présent sur le collecteur de l’étage de façon à pouvoir ramener sur la base de ce transistor un signal en phase avec celui qui était initialement fourni par le générateur. Ensuite, il doit réduire l’amplitude du signal présent sur le collecteur, de façon que l’on ait sur la base un signal de même amplitude que précédemment.

Dans le cas du schéma de la figure 2, le réseau de réaction est constitué par le secondaire S du transformateur accordé et par la résistance R₄. Le premier a pour rôle d’inverser la phase et de réduire l’amplitude, la seconde a comme simple rôle la réduction de l’amplitude ; R₄ a été choisie réglable de façon à pouvoir ramener le signal réinjecté sur la base parfaitement identique à celui qui était injecté auparavant par le générateur, c’est-à-dire de façon à ce que le gain soit égal à 1.

On peut remarquer tout de suite qu’obtenir la condition du gain égal exactement à 1 est difficilement réalisable en pratique, car l’élément variable (R₄) devrait être continuellement retouché. En effet, il suffit de se rappeler que le gain du transistor dépend de la température ambiante, du point de fonctionnement, de l’amplitude du signal appliqué sur la base, et qu’il varie avec l’épuisement de la pile d’alimentation et le vieillissement même du transistor.

Voyons donc brièvement les deux cas qui peuvent se présenter en pratique, lorsque le gain n’est pas exactement égal à 1, mais un peu plus grand ou petit que 1.

Lorsque le gain est plus petit que 1 (ceci peut être obtenu facilement avec le montage de la figure 2 en augmentant légèrement la valeur de R₄), le courant dans la résistance R_e se réduit ainsi que la tension à ses bornes. Si l’inverseur est en position 1 le signal à la sortie est plus faible que celui qui est appliqué à l’entrée par le générateur.

Si l’on place maintenant l’inverseur en position 2, on voit que le signal ramené à l’entrée n’a plus la même amplitude. Comme le signal de sortie est plus petit que le signal à l’entrée (gain inférieur à 1) le signal ramené à l’entrée est encore plus faible ; le signal amplifié que l’on va recueillir à la sortie sera encore plus petit que celui à l’entrée et ainsi de suite.

On se rend compte, ainsi, que le signal va rapidement décroître et qu’il va s’annuler très vite.

Supposons au contraire que le gain est légèrement plus grand que 1 (ce que l’on peut réaliser facilement en réduisant un peu la valeur de R₄, de façon à ce que le courant qui circule dans R_e soit un peu plus grand et qu’ainsi la tension qui se développe aux bornes de R_e soit elle aussi un peu plus grande). Si nous partons maintenant avec les inverseurs en position 1, nous obtiendrons à la sortie un signal un peu plus grand que celui de l’entrée. Si nous basculons les inverseurs en position 2, le signal ramené à l’entrée sera un peu plus grand que celui qui était appliqué auparavant, le signal à la sortie qui va en résulter sera encore un peu plus grand et ainsi de suite ; le signal de sortie va croître de plus en plus.

Théoriquement le signal devrait croître sans cesse et devenir infini. En réalité, il va être limité par la tension d’alimentation, les conditions de polarisation du transistor ainsi que le type du transistor utilisé, comme nous l’avons vu lors de l’étude des amplificateurs. Le signal commence à croître d’abord très rapidement puis de plus en plus lentement ; le transistor, commandé par un signal dont l’amplitude est de plus en plus grande, atteint d’une part la saturation et d’autre part l’interdiction.

A un moment donné donc, le signal de sortie n’augmente plus autant que le signal à l’entrée. Le signal d’entrée continue à augmenter jusqu’à ce qu’on atteigne le point où le gain est égal à 1. Au-delà de ce point, le signal d’entrée ne peut plus augmenter, puisque le gain deviendrait inférieur à 1.

En conclusion, quand le gain de l’étage est plus petit que 1 (signal à la sortie plus petit que celui à l’entrée), le circuit ne peut se "maintenir en oscillation" et les oscillations s’amortissent très rapidement : le circuit se comporte comme un simple amplificateur en ce sens qu’il ne peut y avoir de signal à la sortie que si l’on applique à l’entrée un signal délivré par le générateur.

Quand le gain est plus grand que 1 (signal à la sortie plus grand que celui à l’entrée) non seulement le circuit se maintient en oscillation, mais encore le gain se règle automatiquement à 1, condition nécessaire pour que l’amplitude des oscillations reste constante.

Par rapport au circuit idéal de la figure 2 réglé pour avoir un gain de 1, le circuit réel, avec le gain supérieur à 1, présente un autre avantage. Comme nous l’avons vu, quand le gain est réglé exactement à 1, le circuit ne peut se maintenir en oscillation qu’après que l’on ait basculé l’inverseur de la position 1 à la position 2 et que l’on ait injecté avant un signal provenant d’un générateur. Cette manœuvre n’est absolument pas pratique et doit être répétée toutes les fois que l’on veut amorcer les oscillations.

Au contraire, quand le gain est supérieur à 1, le circuit peut "s’amorcer" par lui-même. Il suffit en effet qu’un signal quelconque se trouve sur la base du transistor pour se trouver immédiatement amplifié, puis reporté à l’entrée, réamplifié à nouveau, et ainsi de suite, jusqu’à ce que les conditions vues précédemment se trouvent vérifiées et que le circuit se maintienne en oscillation.

On n’a pas besoin non plus que le signal "amorcé" sur la base soit à la même fréquence que celle sur laquelle est accordé le circuit résonnant du collecteur : il suffit d’un signal quelconque et d’amplitude aussi faible que l’on veut. En effet, il suffit qu’il soit amplifié successivement : le circuit du collecteur, de par sa propriété sélective, va le rendre de plus en plus sinusoïdal au fur et à mesure que son amplitude va augmenter.

D’autre part, dans un circuit dont le gain est supérieur à 1, il n’est donc pas nécessaire de disposer d’un générateur et de deux inverseurs pour "amorcer" les oscillations. Il suffit de laisser en permanence la sortie reliée à l’entrée par l’intermédiaire du réseau de réaction ; dès que l’on alimente le circuit, les oscillations se produisent spontanément.

Le faible signa initial nécessaire à l’accrochage des oscillations existe toujours en pratique, comme par exemple le courant qui commence à traverser la liaison de base quand on branche l’alimentation.

En conclusion, nous dirons qu’un oscillateur n’est autre qu’un amplificateur dont la sortie est reliée à l’entrée par l’intermédiaire d’un réseau de réaction opportun de façon que le gain de l’étage (le réseau de réaction compris) soit un peu plus grand que 1. La fréquence des oscillations produites sera déterminée par la résonance du circuit de collecteur, lorsqu’il s’agira d’un amplificateur sélectif du type de la figure 2, ou bien par les caractéristiques du réseau de réaction quand (nous le verrons plus tard) l’amplificateur est du type apériodique.

2 – 1 OSCILLATEURS LC

Les oscillateurs LC sont obtenus en partant d’un amplificateur sélectif dont la charge est accordée et constituée par une self L et une capacité C. Des valeurs de L et de C dépend la fréquence des oscillations qui, en première approximation, est donnée par la formule :

f = 159/√(L x C)

où f sera en Hz,kHz ou MHz si L et C sont exprimées respectivement en H et µF ou en mH et nF (kpF) ou µH et pF.

La valeur de C comprend non seulement la capacité du condensateur placée en parallèle sur l’inductance, mais aussi les différentes capacités parasites du transistor et du câblage qui viennent se mettre en parallèle sur L, exactement de la même façon que vu précédemment à propos des amplificateurs accordés.

En choisissant convenablement les valeurs de L et de C, on pourra réaliser des oscillateurs soit BF, soit HF. Dans le premier cas, les valeurs de L et de S seront élevées ; la self sera bobinée sur un noyau en fer ou en ferrite. Dans le second cas, la self sera bobinée sur un mandrin isolant comprenant un noyau de ferrite pour le réglage, tout comme dans le cas des transformateurs FI étudiés dans les leçons précédentes.

Comme le fonctionnement est identique dans tous les cas (BF ou HF) les schémas seront semblables).

Je vous ai représenté en figure 3, la version pratique du schéma de la figure 2. Comme vous pouvez le voir, il s’agit toujours d’un oscillateur à transistor fonctionnant en émetteur à la masse. Les résistances R₂, R₃ et R₄ servent à la polarisation et à la stabilisation thermique du transistor. Le circuit résonnant qui détermine la fréquence des oscillations est placé dans le collecteur et le circuit de réaction est constitué par le secondaire L₁, bobiné directement sur l’enroulement L, et branché directement dans le circuit de base. Les condensateurs C₃ et C₄ offrent un passage facile à la composante alternative des courants de base et d’émetteur qui sinon devrait traverser les résistances R₃ et R₄.

L’enroulement de réaction a un nombre de spire beaucoup plus faible que celui de l’inductance L ; le nombre exact de spires de L₁ dépend du type du transistor utilisé, du point de fonctionnement choisi et de la fréquence de fonctionnement.

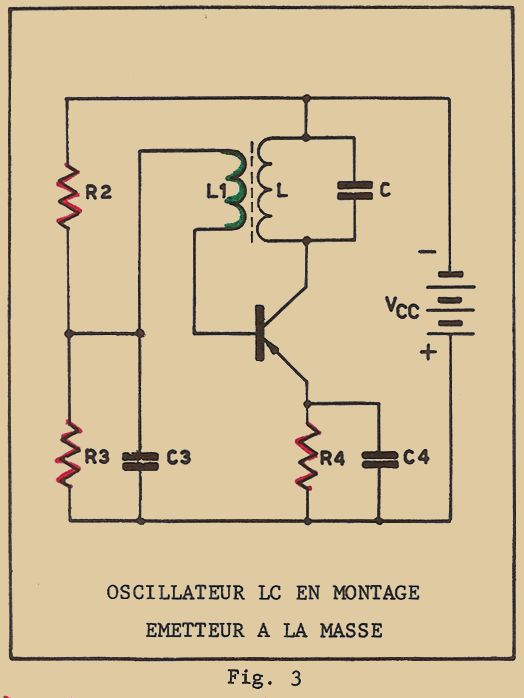
Lorsque l’oscillateur est du type HF et à fréquence variable, on utilise en général un condensateur variable et le nombre de spires de L₁ est déterminé expérimentalement de façon à obtenir un fonctionnement correct dans toute la gamme.

Quand le transistor fonctionne en montage base à la masse, le schéma de l’oscillateur est du type de la figure 4 ; un tel montage est souvent employé dans les oscillateurs changeurs de fréquence des récepteurs radio.

Le circuit de collecteur est couplé au circuit résonnant LC à travers l’enroulement primaire L₁. De cette manière on obtient le même résultat qu’avec la prise intermédiaire sur les transformateurs FI, c’est-à-dire qu’on peut réduire la valeur de la capacité C (comme déjà vu dans la précédente leçon), ce qui est d’une très grande importance surtout lorsqu’il s’agit d’utiliser un condensateur variable qui peut alors être de faible valeur et de petites dimensions.

Le circuit de réaction est constitué par le secondaire L₂ qui ramène un signal convenable en amplitude et en phase dans le circuit de l’émetteur au lieu que ce soit dans le circuit de la base comme c’était le cas dans la figure 3. Les résistances R₂, R₃, R₄ et le condensateur C₄ jouent le même rôle que dans le schéma de la figure 3. L’ordre de grandeur des valeurs des composants est donné en figure 4 (le transistor utilisé comme oscillateur est un SFT 308) Si on utilise un condensateur variable de 6pF 110pF, l’enroulement L comportera 43 spires, L₁-8 spires et L₂-2 spires. Ces enroulements sont bobinés sur un mandrin de 12 mm ; le fil est un fil de "litz" constitué de 32 conducteurs de 4/100mm.

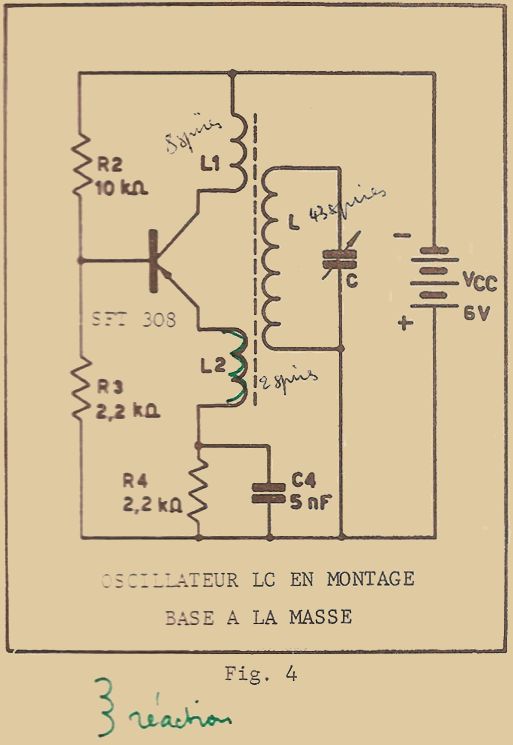
On peut s’arranger, dans le circuit de la figure 4, de façon à avoir la base du transistor "libre" c’est-à-dire de manière qu’aucune tension alternative n’y soit présente ; la seule tension présente est alors la composante continue de polarisation. Ceci peut être intéressant dans le cas où l’on doit appliquer un autre signal au transistor, lorsque ce dernier fonctionne en changeur de fréquence.

Un autre avantage du montage oscillateur en base commune est de pouvoir obtenir des fréquences beaucoup plus élevées. En effet, il suffit de se rappeler qu’au fond le transistor travaille toujours comme un amplificateur et que la fréquence de coupure est beaucoup plus élevée en montage base commune qu’en émetteur à la masse.

Un autre type d’oscillateur LC appelé Hartley, est représenté en figure 5. La particularité de ce circuit réside dans la manière d’obtenir la réaction.

Comme vous pouvez le voir d’après le schéma, l’inductance du circuit résonnant comporte une prise intermédiaire reliée à la pile d’alimentation.

L’inductance L se trouve ainsi partagée en deux sections : L_A qui constitue le circuit du collecteur et L_B celui de la réaction.

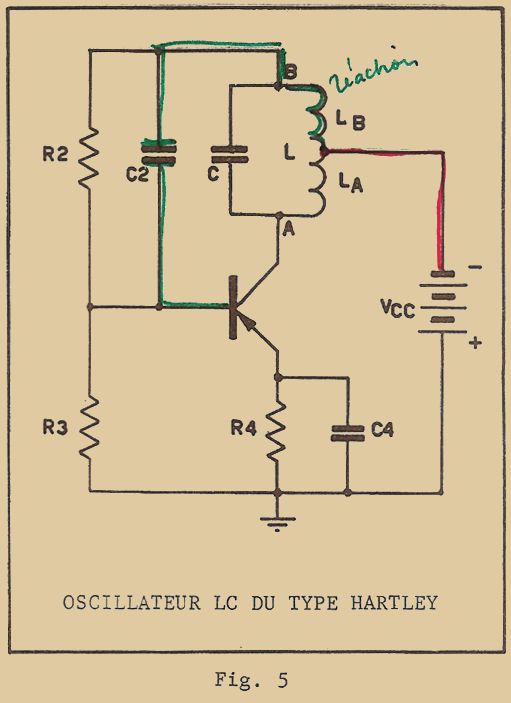
On peut en effet considérer L_A et L_B comme le primaire et le secondaire d’un transformateur ; aux bornes de L_B on obtient une tension en opposition de phase avec celle qui se développe aux bornes de L_A.

On peut aussi faire un raisonnement différent. Considérons la tension totale qui constitue le signal HF présent aux bornes AB du circuit résonnant de la figure 5 ; pendant l’alternance positive du signal, supposons que le point A est positif de 10 V par rapport au point B.

Supposons encore pour simplifier que la prise intermédiaire se trouve exactement au milieu de l’enroulement c’est-à-dire que le nombre de spires de l’enroulement L_A est le même que celui de L_B. Nous dirons alors que, pendant l’alternance positive, le point A se trouve à un potentiel positif de 5 V par rapport à la prise centrale et qu’à son tour, cette prise se trouve à un potentiel positif de 5 V par rapport au point B (le point A se trouve bien à un potentiel positif de : 5 + 5 = 10 V par rapport au point B.

Mais dire que la prise centrale se trouve à un potentiel positif de 5 V par rapport au point B revient à dire que le point B se trouve à un potentiel négatif de 5 V par rapport à la prise intermédiaire. La prise centrale se trouve d’autre part au potentiel de la masse (en effet elle est reliée à la masse par l’intermédiaire de la pile et cette dernière se comporte pour la composante alternative comme un court-circuit).

Nous en conclurons donc que le point A se trouve à un potentiel positif de 5 V par rapport à la masse tandis que le point B se trouve à un potentiel négatif de 5 V par rapport à cette même masse.

Ainsi, en reliant à la masse la prise centrale de L, les points A et B se trouvent constamment à des potentiels de sens opposé (en opposition de phase). On peut donc prélever à partir du point B le signal requis par la réaction.

Le signal de réaction prélevé du point B est ramené sur la base par l’intermédiaire du condensateur C2 : on évite ainsi qu’il ne soit atténué par la présence de R₂. Cette résistance (R₂) sert en effet à polariser la base et le courant de polarisation est prélevé au travers de l’enroulement de réaction L_B.

Un autre oscillateur, semblable au précédent, est appelé COLPITTS (du nom de son inventeur). Le principe de fonctionnement est identique en ce sens que l’on crée encore une prise intermédiaire sur le circuit résonnant pour prélever le signal de réaction.

La différence par rapport à l’oscillateur Hartley est la suivante : la prise intermédiaire est obtenue en divisant le condensateur d’accord du circuit résonnant en deux condensateurs en série C_A et C_B ; le point de jonction est directement mis à la masse (figure 6).

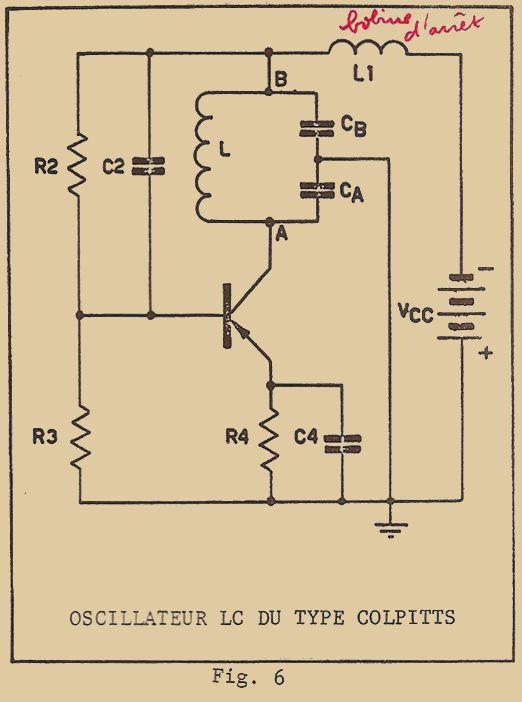
Comme il n’y a plus de prise intermédiaire sur l’inductance pour alimenter l’oscillateur, il faut maintenant l’alimenter par le point M. Mais comme au point B, on trouve le signal de réaction, il est nécessaire maintenant de l’alimenter à travers la self L₁ de forte valeur (self de blocage) dont le rôle est d’empêcher que le signal de réaction ne soit court-circuité vers la masse à travers la pile d’alimentation. On appelle encore L₁ "bobine d’arrêt".

La capacité d’accord C est maintenant :

C = (C_A x C_B)/(C_A + C_B )

Les oscillateurs Hartley et Colpitts présentés en figure 5 et 6 sont réalisés en montage émetteur à la masse. Ils peuvent aussi être réalisés en montage base à la masse en transposant les schémas.

De la position de la prise intermédiaire sur la bobine L (figure 5) et du choix des valeurs de C_A et C_B (figure 6) dépend l’amplitude du signal de réaction qui doit être d’une part suffisante pour amorcer les oscillations mais aussi d’autre part, "raisonnable" pour ne pas distordre les oscillations produites. La position "optimum" de la prise et les valeurs "correctes" des condensateurs sont en général déterminées expérimentalement.

2 – 2 OSCILLATEURS RC

Les oscillateurs dérivent en général d’un amplificateur de type apériodique (c’est-à-dire dont la charge est constituée par une simple résistance) à un ou plusieurs étages, et dont la sortie et l’entrée sont reliées au travers d’un réseau ne contenant que des résistances et des capacités. La fréquence des oscillations produites est déterminée, non pas par la fréquence de résonance d’un circuit résonnant, mais par les caractéristiques de ce réseau de réaction.

Illustrons tout ceci en examinant un type d’oscillateur RC très simple constitué par un seul transistor. Nous partirons donc d’un amplificateur normal à charge résistive et utiliserons un réseau de réaction qui effectuera l’inversion de phase.

Le schéma d’un tel type d’oscillateur est donné en figure 7. Vous y distinguez nettement l’amplificateur apériodique et le réseau de réaction.

L’amplificateur apériodique est constitué par le transistor polarisé à l’aide des résistances R₂, R₃ et R₄ et par la charge R_C.

Le condensateur C₄ a comme simple rôle de supprimer la contre-réaction en alternatif dûe à la résistance R₄ (ce qui ferait diminuer le gain). La charge étant purement résistive (RC), l’étage peut amplifier une large bande passante. Il n’est pas apte par contre à déterminer la fréquence de l’oscillation car il n’a pas de fréquence caractéristique propre, comme c’était le cas avant avec l’amplificateur sélectif.

Le réseau de réaction est constitué de trois cellules RC placées les unes derrière les autres entre le collecteur et la base (marquées I, II et II sur la figure 7.

Les trois condensateurs C ont la même valeur, ainsi d’ailleurs que les trois résistances R. A noter toutefois que la résistance R de la troisième cellule est composée en partie de la résistance R_e de l’étage en série avec la résistance R’ dont la valeur sera obligatoirement :

R – R_e. Ainsi par exemple si l’on prend R = 10kΩ et que la résistance R_e d’entrée de l’étage est 1kΩ, la résistance de la troisième cellule sera égale à : 10 – 1 = 9kΩ

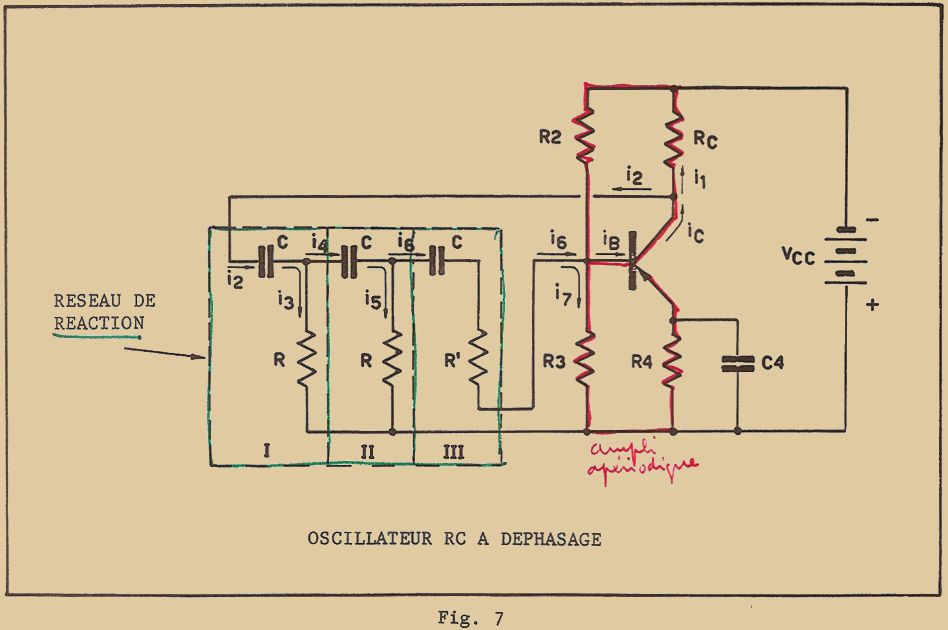
Un tel réseau a la propriété (à cause de la présence des condensateurs), de déphaser le courant alternatif qui le traverse. Ainsi le courant de sortie du réseau (c’est-à-dire le courant de commande de l’étage) est en opposition de phase par rapport au courant d’entrée du réseau (c’est-à-dire le courant alternatif de collecteur). C’est pour cette raison que l’oscillateur de la figure 7 prend aussi le nom "d’oscillateur RC à déphasage". Le déphasage introduit par la cellule de réaction dépend des valeurs de R et de C.

Ayant fixé les valeurs de R et C, on démontre qu’il n’existe qu’une seule valeur de fréquence pour laquelle le courant de sortie de la cellule est exactement en opposition de phase par rapport à celui d’entrée. Ce sera donc la fréquence d’oscillation.

La fréquence est donnée par la formule : f = 65/(R x C)

où la fréquence est exprimée en kHz si la résistance est en kΩ et la capacité en nF. Ainsi par exemple, si R = 10kΩ et la capacité = 5nF (= 5.000pF) la fréquence d’oscillation sera

f = 65/(10 x 5) = 65/50 = 1,3kHz

Cette valeur de la fréquence d’oscillation est théorique et peut différer sensiblement de la fréquence obtenue en pratique ; ceci est surtout dû au déphasage introduit par le transistor lui-même, qui est d’autant plus sensible que le transistor fonctionne plus près de sa fréquence de coupure.

En examinant le schéma de la figure 7, on pourra remarquer comment le courant i_c (c’est-à-dire la composante alternative du courant du collecteur ou en d’autres termes, le courant du signal de sortie du transistor) se partage en un courant i₁ qui traverse R_C et un courant i₂ qui constitue le courant d’entrée de la cellule de réaction.

A son tour le courant i₂ se partage en i₃ et i₄ qui lui-même se partage en i₅ et i₆. Le dernier enfin se partage en i₇ et i_B. A cause même de cette division, le courant qui atteint la base est notablement réduit par rapport à celui du collecteur.

La théorie annonce, que dans le meilleur des cas, le courant i_B ne peut être au maximum que le trentième du courant i_C.

Ceci signifie donc, que pour que le circuit puisse osciller, il faut que le courant i_C soit au moins trente fois plus grand que iB, ce qui équivaut à dire que le transistor doit avoir un coefficient d’amplification en courant d’au moins 30.

Le circuit de la figure 7 ne peut donc être utilisé en pratique que seulement avec des transistors dont le β est supérieur à 30.

De ce qui vient d’être dit, il résulte que le circuit de la figure 7 ne pourra être réalisé en montage base à la masse, car dans ce cas le coefficient d’amplification en courant est toujours inférieur à 1, et le courant de sortie du transistor est toujours inférieur à celui de commande ; aucun transistor ne peut satisfaire les conditions vues précédemment.

Le schéma de la figure 8 dérive directement de celui de la figure 7 en permutant capacités et résistances dans la cellule de réaction.

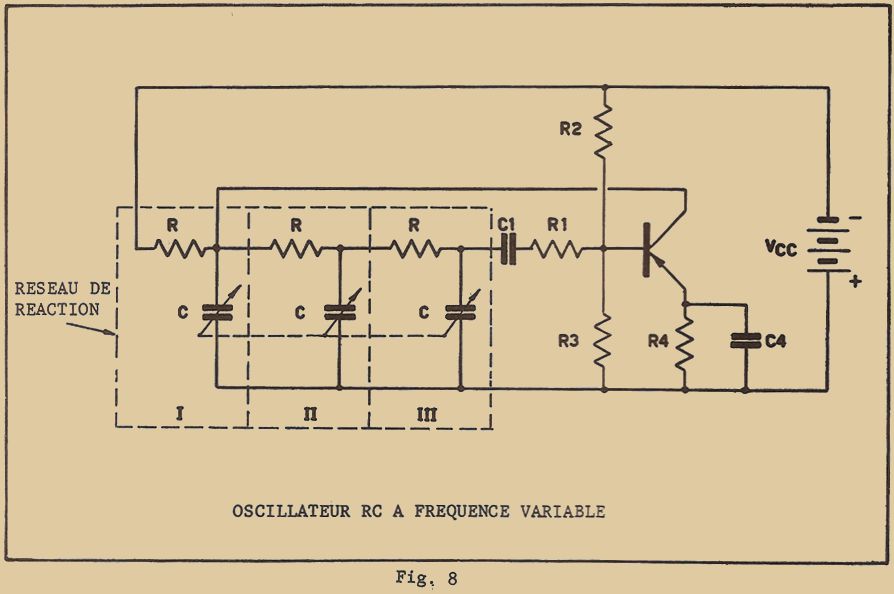
On aura donc trois résistances R d’égale valeur montées en série et trois condensateurs reliés vers la masse. Les rectangles en pointillés indiquent les trois cellules.

Vous noterez encore que la première résistance sert en même temps de résistance de charge collecteur. Le condensateur C1 joue seulement un rôle de liaison, et évite que la composante continue du courant de collecteur n’atteigne la base. La résistance R₁ a comme seul rôle d’éviter que la faible valeur de la résistance d’entrée R_e de l’étage ne perturbe le fonctionnement du réseau de réaction.

A part ces remarques, le fonctionnement du schéma de la figure 8 est identique à celui du schéma de la figure 7. La formule pour déterminer la fréquence d’oscillation avec les mêmes limitations qu’énoncées précédemment est la suivante :

f = 390/(R x C)

où f est encore exprimée en kHz si R est donné en kΩ et C en nF.

En reprenant l’exemple de la figure 7, où R = 10.000Ω = 10kΩ et C = 5.000pF = 5nF, la fréquence est maintenant :

f = 390/(R x C) = 390/(10 x 5) = 390/50 = 7,8kHz = 7.800Hz

On voit tout de suite que la fréquence avec cette disposition des éléments est six fois plus élevée que précédemment (7,8 = 6 x 1,3kHz).

Par rapport au schéma de la figure 7, le schéma de la figure 8 a l’avantage de délivrer un signal plus sinusoïdal et d’être mieux adapté dans le cas où l’on désire réaliser un oscillateur à fréquence variable. En effet, dans ce schéma, les trois condensateurs de la cellule de réaction ont une connexion commune reliée à la masse ce qui permet d’utiliser un condensateur variable à trois cages du type classique et où les armatures mobiles des trois sections sont commandées par un axe unique et reliées électriquement entr’elles (figure 8).

3 – STABILITÉ EN FRÉQUENCE ET EN AMPLITUDE

On appelle stabilité en fréquence d’un oscillateur, son aptitude à délivrer un signal dont la fréquence reste constante pendant son fonctionnement. La stabilité en fréquence dépend de la stabilité de tous les composants qui interviennent dans la détermination de la fréquence, c’est-à-dire stabilité des valeurs de l’inductance et de la capacité dans les circuits LC et stabilité des valeurs des résistances et des capacités dans les circuits RC.

Dans tous les cas, interviennent aussi (plus ou moins) les caractéristiques des transistors. La stabilité en fréquence dépend donc aussi de ces dernières.

Tandis que sur les valeurs de l’inductance, des capacités et des résistances, la température joue un rôle plus ou moins évident et sensible, cette dernière a une influence décisive sur les transistors. Le vieillissement des composants a aussi son mot à dire. Par contre, la variation des tensions d’alimentation joue un rôle déterminant sur la stabilité de la fréquence à cause des variations qu’elle entraine dans les paramètres des transistors.

Pour obtenir une bonne stabilité en fréquence, il faut en premier lieu faire en sorte qu’elle dépende le moins possible des transistors.

Il faut se rappeler en effet que le transistor intervient dans la détermination de la fréquence grâce au déphasage qu’il introduit ; il faut noter aussi que le signal sur le collecteur n’est jamais en parfaite opposition de phase avec celui qui existe sur la base et ceci d’autant moins que la fréquence d’oscillation se rapproche plus de la fréquence de coupure du transistor.

Ainsi, pendant le fonctionnement, le déphasage introduit par le transistor augmente ou diminue entrainant une variation de la fréquence. Comme ce déphasage s’ajoute à celui introduit par la cellule de réaction, il est évident que l’influence du transistor se manifeste plus dans le cas des oscillateurs RC que dans celui des oscillateurs LC.

En effet, comme nous l’avons vu, la fréquence d’oscillation des premiers est donnée par le réseau de réaction. Ainsi si l’on désire que la fréquence soit stable, il faut faire en sorte qu’une variation en sens contraire se produise de façon à maintenir constante la fréquence du signal.

Dans le cas des oscillateurs LC, au contraire, la fréquence est déterminée par la résonance du circuit accordé, qui dépend presque exclusivement des valeurs de L et de C et se ressent donc peu des déphasages introduits par le transistor.

De tout ce qui vient d’être dit, il ressort que les oscillateurs LC sont beaucoup plus stables que ceux en RC. D’autre part, pour réduire l’influence du transistor sur la fréquence d’oscillation il faut que ce dernier ne travaille pas trop près de sa fréquence de coupure et que ses paramètres restent aussi constants que possible. Pour cela, il faut le stabiliser en température et en tension d’alimentation.

En ce qui concerne les circuits LC, il faut encore ajouter que la fréquence sera d’autant plus stable que le facteur de qualité Q du circuit résonnant sera plus élevé.

On appelle stabilité en amplitude d’un oscillateur son aptitude à maintenir constante l’amplitude des oscillations produites, qui ne dépend que très peu des composants et presque exclusivement du gain du transistor.

Pour obtenir une bonne stabilité en amplitude, il faut stabiliser le plus possible le gain du transistor, ce que l’on obtient encore en stabilisant la température et les tensions d’alimentation et en utilisant des réseaux de contre-réaction qui ont la propriété comme nous le verrons ultérieurement de stabiliser le gain.

Il faut encore remarquer que l’amplitude des oscillations croît jusqu’à saturer l’étage. Ainsi plus l’étage est saturé, plus l’amplitude des oscillations est stable ; par contre le signal est alors distordu et est très loin de sa forme sinusoïdale.

Comme la saturation de l’étage dépend de l’amplitude du signal ramené à l’entrée, il est évident que l’on peut trouver un compromis entre une bonne stabilité en amplitude et une forme sinusoïdale correcte en agissant, soit sur l’amplitude du signal de réaction, soit sur le gain de l’étage. La stabilité en amplitude dépend donc en grande partie comme nous l’avons prévu de la cellule de réaction.

---

EXERCICES DE RÉVISION SUR LA 25^ème LEÇON THÉORIQUE

1 – Qu’appelle-t-on un oscillateur ?

2 –Quelle différence y a-t-il entre un oscillateur BF et un HF ?

3 – Quand dit-on qu’un oscillateur est LC et quand est-il RC ?

4 – Qu’appelle-t-on cellule (ou réseau) de réaction ?

5 – Quelles sont les propriétés d’un réseau à réaction ?

6 – Quelles sont les possibilités d’un étage dont le gain est supérieur à 1 ?

7 – Quel est l’avantage d’un oscillateur LC en montage base à la masse par rapport à celui en montage en émetteur commun ?

8 – Quelle est la différence principale entre un oscillateur Hartley et un Colpitts ?

9 – Pourquoi un oscillateur RC à déphasage ne peut fonctionner en base à la masse ?

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 24^ème LEÇON THÉORIQUE

1 – Le coefficient Q_o est donné par :

Q_o = X_o/R_f = 300/5 = 60

2 – R_p = Q_o² x R_f = (60)² x 5 = 18.000Ω = 18kΩ

3 – On sait que X_o = Lω_o et que Q_o = (Lω_o)/R_f (= X_o/R_f )

D’où :

R_p = Q_o² x R_f = (Lω_o/R_f)² x R_f

 = (L² ω_o²)/(R_f²) x R_f = (L²ω_o²)/R_f

4 – Calculons tout d’abord ω_o

ω_o = 2πf_o = 2 x 3,14 x 300Hz = 1884

(ω_o)² = (1884)2 = 3.550.000 environ

D’où R_p = (L² ω_o² )/R_f = (4 x 3.550.000)/100 = 142.000Ω = 142kΩ

5 – L’"effet pelliculaire" ou "effet de peau" est le phénomène dans lequel la résistance d’un conducteur augmente lorsque la fréquence du courant qui la traverse croît.

6 – Un fil dit de "litz" est un conducteur formé de plusieurs fils de faible section, torsadés entr’eux et isolés. Il est avantageux par rapport à un conducteur unique de section égale pour la résistance plus faible qu’il offre aux courants de fréquences élevées.

7 – Dans un transformateur où le primaire seul est accordé, le secondaire est bobiné directement sur le primaire. Dans le cas, où primaire et secondaire sont simultanément accordés, les deux enroulements sont bobinés séparés et à une certaine distance entr’eux.

8 – Par couplage critique, on indique que l’on atteint à la fréquence de résonance, la tension maximum possible.

9 – Lorsque le couplage est supérieur au couplage critique, la courbe de réponse présente un creux à la fréquence de résonance du primaire et du secondaire.

Fin de la leçon 25

---

LECON 26

1 – RÉCEPTEURS RADIO A TRANSISTORS

Nous avons étudié jusqu’à maintenant la physique des semi-conducteurs, puis le fonctionnement des transistors. Nous avons examiné aussi les amplificateurs en général : BF, préamplificateurs en tension et amplificateurs en puissance. Ensuite, nous avons vu les amplificateurs HF et les circuits oscillateurs. Nous avons ainsi réuni tous les éléments nécessaires pour commencer l’étude des récepteurs radio à transistors ; il suffit, en effet, de réunir pour ainsi dire tous les circuits élémentaires déjà étudiés pour réaliser un circuit plus complexe comme celui d’un récepteur.

Pour cela, il convient tout d’abord d’examiner la composition d’un récepteur à l’aide d’un schéma-bloc. Ainsi, les différentes parties du récepteur sont indiquées par convention, par un simple rectangle dans lequel est inscrite la fonction spécifique de l’étage.

En général, chaque rectangle représente un étage comprenant un seul transistor. Quelquefois cependant, le rectangle pourra englober deux transistors (comme par exemple dans le cas où l’étage de sortie est un push-pull) ou bien une diode (comme dans le cas d’un détecteur) ou bien ni transistor ni diode (quand il représentera un montage particulier ne comportant aucun semi-conducteur mais restant toutefois d’importance assez fondamentale pour être mis en évidence : par exemple le réglage du volume ou le contrôle de tonalité).

Un récepteur en modulation d’amplitude (AM) peut ainsi être représenté par le schéma-bloc de la figure 1. En suivant le signal de l’antenne vers le haut-parleur, nous rencontrerons les étages suivants.

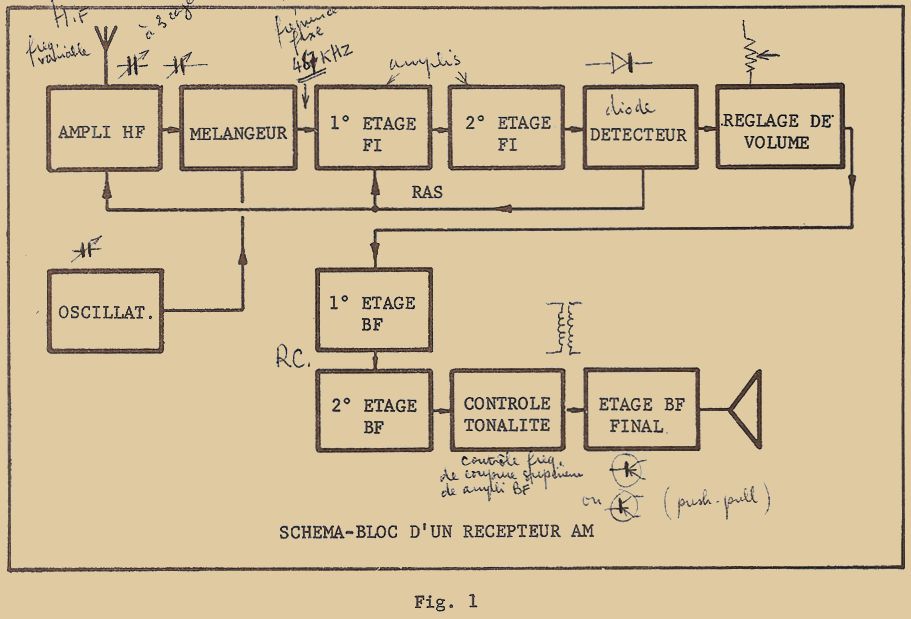
Le signal est capté par l’antenne et amplifié par l’étage HF qui sera donc du type sélectif à fréquence d’accord variable et pouvant être accordé sur la fréquence du signal que l’on désire recevoir.

On trouve ensuite l’étage mélangeur qui avec l’oscillateur constitue le changeur de fréquence dont le rôle est, comme son nom l’indique, de changer la fréquence du signal en une fréquence de valeur fixe qui est en général de 480kHz (ou 455kHz ou 467kHz selon les constructeurs). Cette fréquence fixe est appelée fréquence intermédiaire.

De cette manière quelle que soit la fréquence du signal reçu, le signal à la sortie du mélangeur aura toujours pour valeur 467kHz et pourra ainsi être énergiquement amplifié par les étages FI qui travaillant à fréquence fixe présentent de notables avantages par rapport à ceux qui fonctionnent à fréquence variable, tant du point de vue des caractéristiques électriques, que du point de vue de la réalisation et du prix de revient.

En effet, si l’on ne fait pas de changement de fréquence, tous les étages qui précèdent le détecteur doivent être accordés sur la fréquence du signal reçu de façon à pouvoir présenter les caractéristiques de sélectivité indispensable à la séparation de l’émetteur reçu parmi tous les autres.

Le circuit d’entrée du premier étage et tous les transformateurs de liaison placés entr’étages devront être du type à accord variable et réalisés par des inductances ou des condensateurs variables.

Ainsi, dans le cas de l’accord par condensateurs variables, des complications mécaniques apparaissent ; le condensateur variable devra être composé de plusieurs cages : autant de cages qu’il a d’étages, plus un pour le circuit d’entrée du premier étage. Si l’on voulait utiliser des transformateurs à primaire et secondaire accordés, le nombre de cages serait doublé.

La complication mécanique est encore plus grande, s’il s’agit d’accorder les circuits par des inductances variables, car il faut alors déplacer simultanément tous les noyaux des inductances. Cette complication devient infernale, si le récepteur comporte plusieurs gammes d’ondes car il faut alors prévoir la commutation de tous les transformateurs pour chaque gamme.

Les inconvénients de caractère électrique deviennent pratiquement insolubles si l’on désire que l’amplification reste constante dans toute une gamme. Ainsi, la sélectivité ne peut rester constante. Il en résulterait que le récepteur serait plus sensible sur certaines fréquences et sa capacité de sélection, c’est-à-dire sa capacité à séparer un émetteur parmi les autres, serait différente d’un point à l’autre de l’échelle.

Si on choisit au contraire la solution du changeur de fréquence, les difficultés se trouvent réduites (à part le circuit d’entrée et la liaison entre l’amplificateur HF et l’étage mélangeur). En effet, tous les autres étages sont à fréquence fixe, c’est-à-dire qu’ils ne nécessitent pas d’une part des systèmes d’accord compliqués et que d’autre part, ce qui est très intéressant, ils présentent des caractéristiques d’amplification et de sélectivité constantes pour les différentes fréquences reçues.

L’inconvénient est l’utilisation d’un changeur de fréquence ce qui nécessite un oscillateur à fréquence variable.

En effet, dans le changement de fréquence, le signal FI naît du battement entre le signal reçu et le signal de l’oscillateur, battement qui se produit dans l’étage mélangeur. Pour que le signal FI soit égal à 480kHz (par exemple), il faut que la fréquence de l’oscillateur diffère de celle du signal reçu de 480kHz exactement.

Dans le cas de la figure 1, la commande d’accord devra agir sur la fréquence d’accord du circuit d’entrée, du circuit de liaison entre l’étage HF et l’étage mélangeur et aussi sur la fréquence de l’oscillateur. On pourra donc utiliser par exemple un condensateur variable à trois cages et à commande unique.

Le signal amplifié par les étages FI est appliqué, comme on peut le voir à la figure 1, à l’étage détecteur, constitué en général par une simple diode quand il s’agit de détecter une onde modulée en amplitude.

Le détecteur délivre à sa sortie deux signaux distincts : un constitué par une tension alternative dont l’allure reproduit fidèlement celui de la modulation du signal reçu et représente le véritable signal basse-fréquence ; l’autre constitué par une tension continue d’amplitude d’autant plus grande que le signal reçu est plus intense, c’est-à-dire qu’il est proportionnel à l’intensité du signal HF capté.

Le signal BF est envoyé à un potentiomètre de volume qui règle l’amplitude du son qui sera émis par le HP. Ensuite ce signal basse fréquence est appliqué au premier étage BF.

Ce signal pourra ensuite être amplifié par un second étage BF qui délivrera un signal d’amplitude convenable pour piloter l’étage final de puissance, qui à son tour fournira la puissance nécessaire pour actionner le haut-parleur.

La liaison entre le premier et le second étage BF est normalement du type à résistance-capacité, tandis qu’entre le second étage et l’étage final, on trouve presque toujours un transformateur. L’étage final à son tour, peut-être du type à un seul transistor en classe A, ou à deux transistors push-pull en classe B.

Entre le second étage BF et le final, peut être placé un contrôle de tonalité comme indiqué sur la figure 1, dont le rôle est de contrôler la fréquence de coupure supérieure de l’amplificateur BF avec comme résultat d’atténuer plus ou moins les fréquences élevées. Dans certains cas, le réglage peut aussi se faire sur les fréquences basses par atténuation ou par expansion.

Le second signal délivré par le détecteur (c’est-à-dire la tension continue d’amplitude proportionnelle à l’intensité du signal reçu) est ramené vers les étages HF et première FI (figure 1). On réalise de cette façon un dispositif appelé réglage automatique de sensibilité (RAS) qui rend le récepteur d’autant moins sensible que le signal reçu est plus intense.

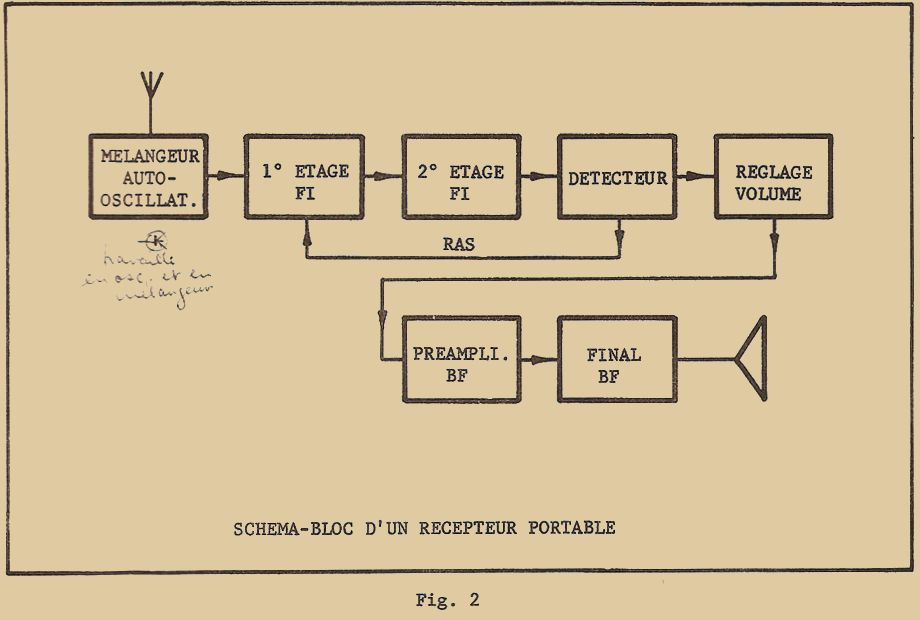
De cette façon, les signaux faibles sont amplifiés plus que les signaux forts. Ainsi, on applique au détecteur des signaux qui ont presque tous la même amplitude et on évite aussi de saturer les étages FI par des signaux forts qui auraient, sans cela, une trop forte amplitude. Avec ce RAS, on obtient une amplitude du signal BF à la sortie du détecteur quasiment constante.

Je vous ai représenté à la figure 2, un schéma-bloc d’un récepteur portable réduit au minimum de composants indispensables.

On a supprimé, dans ce schéma, l’amplificateur HF. Le changeur de fréquence est réalisé par un seul transistor, qui fonctionne simultanément en oscillateur et en mélangeur. Un seul préamplificateur BF est prévu. Le réglage de tonalité est supprimé et le RAS agit seulement sur le premier étage FI.

Nous allons examiner maintenant la constitution des circuits représentés dans le schéma-bloc.

2 – CIRCUIT D’ENTRÉE ET AMPLIFICATEUR HF

L’amplificateur HF, lorsqu’il existe (figure 1), est du type sélectif avec les circuits d’entrée et de sortie accordés sur la fréquence du signal que l’on reçoit.

Son schéma sera analogue à ceux que nous avons vus avec les amplificateurs sélectif_s : le transistor travaillera normalement en montage émetteur à la masse et sera du type adapté pour les gammes de fréquences que nous désirons recevoir, c’est-à-dire que sa fréquence de coupure f_β devra être supérieure à la fréquence maximum à recevoir.

Dans le cas de la réception des petites ondes, on prendra un transistor de fréquence de coupure f_β un peu supérieur à 1,5MHz ; au contraire pour la réception des ondes courtes, f_β devra être supérieur à 15 ou 20MHz.

Le schéma type de l’amplificateur sélectif peut être comme celui qui est représenté en figure 3. Comme à l’habitude les résistances R₂, R₃ et R₄ ainsi que les condensateurs C₃ et C4 servent pour le circuit de polarisation et la stabilisation thermique.

Le point de fonctionnement est choisi pour obtenir à la sortie un gain aussi élevé que possible. Les signaux présents dans le premier étage d’un récepteur sont toujours très faibles et il n’y a aucun danger de saturation.

Le point de fonctionnement est choisi en fonction du bruit de fond produit par le transistor même. En effet, le courant de collecteur d’un transistor quelconque n’est pas parfaitement constant dans le temps, mais subit continuellement des variations produites par la variation d’un instant. à l’autre du nombre de porteurs présents dans le semi-conducteur.

Les variations sont extrêmement faibles et aucun milliampèremètre placé dans le collecteur ne pourra les révéler. La valeur qu’indiquera le milliampèremètre est la valeur moyenne du courant collecteur, qui en réalité subit continuellement des accroissements et des diminutions autour de cette valeur, tout comme si on appliquait à la base un véritable signal.

Les petites variations du courant de collecteur du premier transistor sont transmises au transistor suivant et ainsi de suite. Amplifiés par tous les étages qui composent le récepteur, elles se traduisent dans le haut-parleur par un bruit de fond caractéristique qui ressemble à un souffle superposé à la musique et à la parole.

Il est évident que le souffle perçu dans le haut-parleur est dû presque exclusivement au premier transistor, parce que ce bruit de fond est amplifié par tous les étages successif_s, tandis que le bruit de fond produit par les autres transistors est moins important car il est amplifié par moins d’étages.

Pour réduire le souffle, qui se fait particulièrement sentir lors de la réception de stations lointaines (plus le signal reçu est faible et plus le bruit de fond devient gênant), il faut soigner tout particulièrement l’établissement du projet du premier étage.

Comme d’autre part le bruit de fond produit par un transistor est plus ou moins fort selon la valeur du courant de collecteur, il est clair qu’il faut faire travailler le transistor avec un courant de collecteur bien déterminé pour lequel le souffle est minimum.

Cette valeur du courant de collecteur est en général de l’ordre de 1 mA pour les transistors HF.

Le transformateur de liaison entre TR₁ et TR₂ est constitué par le primaire L₃ et le secondaire L5 et est très semblable aux transformateurs FI avec la seule différence qu’il est à fréquence variable au lieu de fixe. Ici encore, pour pouvoir utiliser un condensateur variable de capacité pas trop élevée, CV₂ n’est pas placé directement aux bornes de L₃, mais sur un prolongement de celle-ci, de la même manière que sur les transformateurs FI.

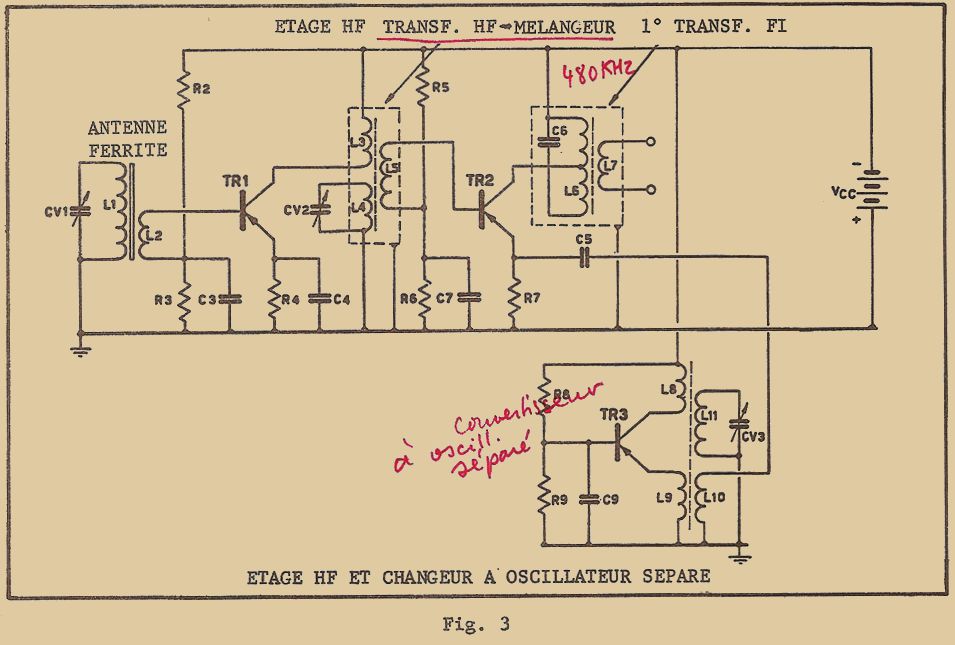
Par contre sur la figure 3, au lieu de prolonger L₃, on fait un troisième enroulement L₄ dont le nombre de spires est supérieur à celui de L₃. ; de cette manière on a l’avantage d’avoir L₄ complètement isolé de L₃ et de pouvoir brancher directement à la masse l’armature de CV₂. Ceci est très commode, car CV₂ forme avec CV₁ et CV3, un condensateur variable à trois cages, dont toutes les armatures mobiles sont réunies entr’elles, électriquement et mécaniquement et, d’autre part, il faut qu’elles soient toutes réunies à la masse.

Les enroulements du transformateur HF (comme ceux d’ailleurs des transformateurs FI) sont bobinés sur un même noyau en matériau ferromagnétique pour hautes fréquences et réglables en général pour pouvoir accorder le circuit sur la fréquence exacte. Le transformateur est enfermé dans un boitier métallique relié à la masse (il est représenté par les traits en pointillés sur la figure 3) ce qui évite des couplages capacitif_s parasites avec d’autres circuits.

Dans les récepteurs petites ondes et grandes ondes (gammes comprises respectivement entre 500kHz et 1500kHz et entre 150kHz et 300kHz environ) le circuit résonnant du premier étage fonctionne aussi comme une antenne, en ce sens qu’il capte directement les ondes radio sans être relié à une antenne extérieure.

On réalise ainsi les antennes dites "ferrite" du fait que l’inductance du circuit résonnant est bobinée sur un bâtonnet de ferrite dont les dimensions sont celles d’un crayon ordinaire.

Le ferrite est un matériau du type céramique constitué par des oxydes et des carbonates de fer et de manganèse ; il présente des propriétés magnétiques élevées mais, comme la céramique, il n’est pas conducteur du courant électrique. Ainsi ses propriétés restent inaltérées même aux fréquences élevées de l’ordre de quelques MHz et plus.

Si un barreau de ferrite est placé dans un champ électromagnétique, comme celui qui est rayonné dans l’espace par une antenne d’émission, de par ses propriétés de perméabilité magnétique élevée il va présenter une très faible réluctance (résistance) aux lignes de flux de la composante magnétique du champ électromagnétique : ces lignes de flux se concentrent donc à l’intérieur du barreau (figure 4a).

La présence du barreau ferrite a pour effet de "condenser" les lignes de flux et de faire en sorte qu’un nombre plus grand de celles-ci passent à l’intérieur du barreau. Le résultat est que l’on obtient aux bornes de la bobine une tension HF plus grande, comme si la bobine était placée dans un champ beaucoup plus intense. Cette tension induite est d’autant plus grande que les dimensions du ferrite sont plus grandes. L’efficacité de l’antenne dépend donc des dimensions du bâtonnet sur lequel est bobinée la self.

Le signal ainsi capté est suffisant pour commander le premier transistor sans avoir à recourir à l’antenne classique constituée par un morceau de fil tendu dans l’air et de longueur convenable.

L’antenne ferrite est en réalité moins efficace que celle formée d’un fil tendu, mais offre les avantages par rapport à cette dernière. Avant tout, il faut remarquer que l’antenne ferrite est appelée aussi "antenne magnétique", car comme on l’a vu elle est sensible uniquement à la seule composante magnétique du champ électromagnétique et la tension HF induite est dûe à une induction magnétique.

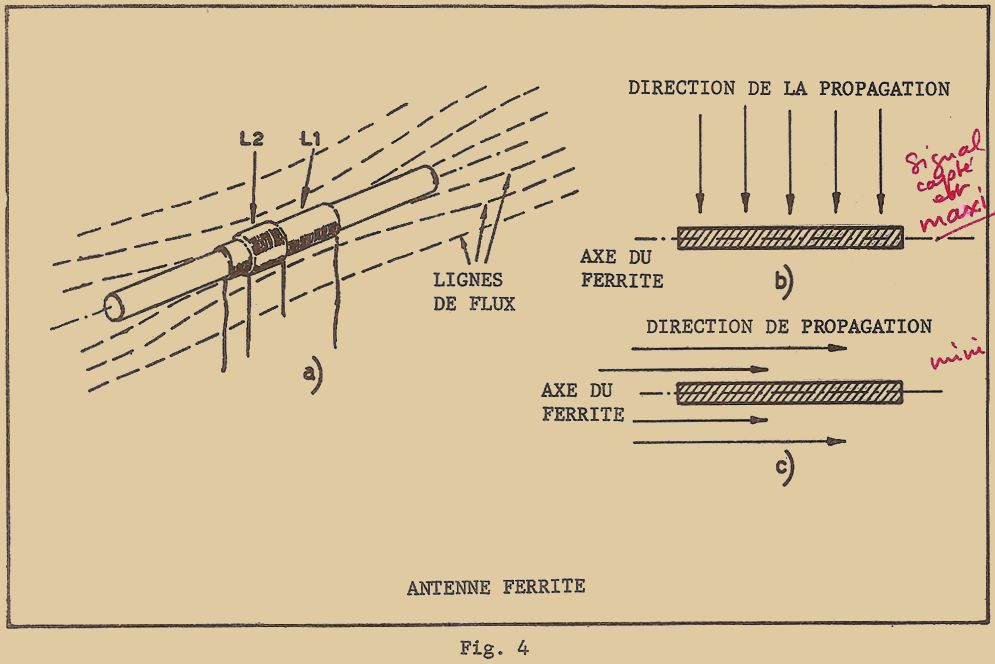
L’autre type d’antenne (fil aérien) s’appelle au contraire "antenne capacitive" car elle est sensible uniquement à la seule composante électrique du champ électromagnétique et la tension HF induite dans le fil l’est par effet capacitif entre le fil et l’espace environnant.

L’avantage que l’antenne magnétique présente par rapport à l’antenne capacitive est dû au fait que la première est sensible seulement à la composante magnétique et la seconde à la seule composante électrique.

Les appareils électriques tels que les moteurs, interrupteurs, etc… se comportent comme de véritables "émetteurs à étincelles" et rayonnant dans l’espace des ondes électromagnétiques discontinues qui se superposent aux ondes des émetteurs perturbent la réception (parasites).

Dans le voisinage de l’appareil qui les produit, la composante électrique du champ électromagnétique perturbateur émis par les étincelles, est beaucoup plus intenses que la composante magnétique ; il en résulte que les parasites induits dans une antenne capacitive sont beaucoup plus intenses que ceux induits dans une antenne magnétique.

En conclusion, nous dirons que l’antenne magnétique est beaucoup plus avantageuse, parce que le signal capté est peut-être moins intense qu’il ne le serait s’il était capté par une antenne capacitive, mais il se trouve moins perturbé ; en d’autres termes nous pourrons dire, (ce qui n’est d’ailleurs pas parfaitement exact) que l’antenne magnétique est moins sensible aux parasites qu’une antenne capacitive.

Une autre caractéristique intéressante de l’antenne ferrite est qu’elle est directionnelle. En effet, elle ne fonctionne correctement que si elle est placée dans la direction des lignes du flux, car, dans ce cas, le flux qui la traverse est maximum et le signal induit dans la bobine est maximum aussi.

Etant donné que la direction des lignes de flux de la composante magnétique du champ électromagnétique est orthogonale à la direction de propagation des ondes radio, on en déduit que le signal capté par l’antenne est maximum quand elle est disposée de façon à ce que son axe soit perpendiculaire à la direction de la propagation (figure 4b) et qu’il est minimum quand son axe est parallèle à la direction de propagation (figure 4c).

D’autre part, comme les lignes de flux sont horizontales (ceci provient du fait que les antennes d’émission sont des pylônes verticaux) les antennes ferrites devront toujours être disposées horizontalement c’est-à-dire orientées pour recevoir un signal d’intensité maximum.

En examinant à nouveau le schéma de la figure 3, il faut encore remarquer qu’en ce qui concerne le circuit d’entrée, le circuit résonnant est constitué par l’enroulement L₁ et par le condensateur variable CV₁. Comme on veut utiliser un condensateur variable, dont la capacité ne soit pas trop élevée, il faut que l’inductance L₁ soit par contre relativement grande. Il va en résulter que le circuit résonnant aura une résistance R_p (voir leçon théorique 21) élevée, et que l’on ne pourra pas le brancher directement sur la base du transistor, étant donné la faible résistance d’entrée.

Il faudra donc prévoir un transformateur entre le circuit résonnant d’antenne et le transistor ; on bobinera donc sur le même bâtonnet de ferrite, un secondaire L₂ constitué par un nombre de spires réduit.

Comme nous l’avons déjà dit, les antennes ferrites travaillent remarquablement dans la gamme des petites et grandes ondes, mais ont une efficacité trop faible pour être utilisées dans la gamme des ondes courtes.

Pour cette gamme de fréquence (et aussi si on veut ne pas utiliser d’antenne ferrite pour les autres gammes), on fait appel à l’antenne capacitive formée par un fil tendu verticalement, ou bien dans le cas des récepteurs portables, ou récepteurs auto, on utilise une antenne télescopique de 1 m de long environ.

Dans ce cas, le circuit d’entrée a l’aspect d’un transformateur HF classique. Le circuit résonnant est constitué par CV₁ et L₁ (figure 5). L’inductance est bobinée sur le noyau et couplée au transistor par l’intermédiaire du secondaire L₂ constitué de quelques spires. Comme l’antenne capacitive présente une impédance relativement basse, elle ne peut être reliée directement à l’extrémité supérieure de L₁, car elle amortirait trop le circuit résonnant et le rendrait peu sélectif. Pour obtenir un rendement maximum de l’antenne, il faut la relier à une prise intermédiaire de L₁, ou tout simplement à l’extrémité supérieure de L₂.

Dans le cas des récepteurs PO et GO, l’antenne capacitive peut encore être branchée directement à l’extrémité supérieure de L₁, par l’intermédiaire d’un condensateur C de faible capacité indiqué en pointillés sur la figure 5. Ce couplage est moins efficace que le précédent et donc peu utilisé.

Le transformateur d’antenne peut ou non être enfermé dans un blindage métallique, comme cela se fait pour les autres transformateurs.

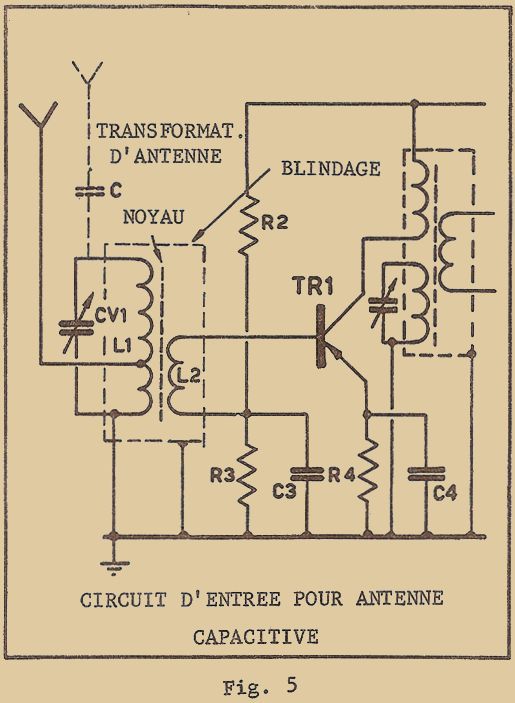
Il faut encore noter qu’on branche quelquefois une antenne capacitive (télescopique) au circuit d’entrée déjà constitué par une antenne magnétique, pour augmenter la faible sensibilité du récepteur, surtout s’il est du type portable.

2 – 1 CONVERTISSEUR A OSCILLATEUR SÉPARÉ

Le convertisseur est formé par un étage oscillateur, constitué par le transistor TR 3 qui fonctionne comme nous l’avons vu dans la précédente leçon et d’un étage mélangeur. Ce dernier est encore principalement un étage amplificateur du type sélectif, quoiqu’un peu particulier.

En effet, son circuit d’entrée est à fréquence variable et accordé sur la fréquence du signal reçu (il est constitué en effet du transformateur de couplage entre TR₁ et TR₂). Le circuit du collecteur est au contraire accordé sur une fréquence fixe (480kHz par exemple) et est constitué par le primaire du premier transistor FI.

On injecte sur l’émetteur de TR₂, par l’intermédiaire de C5, le signal prélevé sur l’oscillateur par l’enroulement spécial L₁₀.

Ainsi, TR₂ est piloté simultanément par le signal reçu, de fréquence f_s, sur sa base et par le signal de l’oscillateur, d’amplitude beaucoup plus grande et de fréquence f_o injecté sur son émetteur.

Le courant de collecteur est ainsi formé de plusieurs composantes : la première composante aura la fréquence f_s du signal appliqué sur la base ; la seconde composante aura la fréquence f_o (en général plus élevée que f_s) du signal appliqué à l’émetteur. Aucune autre composante ne devrait être présente si le transistor fonctionnait dans des conditions normales d’amplification.

Mais, comme je vous l’ai dit plus haut, le signal délivré par l’oscillateur est de très grande amplitude, et amène le point de fonctionnement de TR₂ à l’interdiction pendant les crêtes positives, et à saturation pendant les crêtes négatives.

Il devient donc évident que le transistor dans ces conditions ne peut fonctionner sans distordre les signaux qui lui sont appliqués. Le résultat de ces distorsions se traduit par l’apparition de deux autres composantes : une de fréquence égale à la somme des fréquences des deux signaux appliqués, c’est-à-dire f_o + f_s, l’autre de fréquence égale à la différence de ces deux fréquences, c’est-à-dire f_o – f_s.

Ces deux composantes sont appelées "composantes de battement" en ce sens qu’il naît un battement entre les deux signaux appliqués à l’étage mélangeur.

Si l’on s’arrange de façon qu’en faisant varier le condensateur variable, (c’est-à-dire que CV₁, CV₂ et CV3 varient simultanément) la fréquence f_o de l’oscillateur reste toujours supérieure (de 480kHz par exemple) à celle d’accord des deux autres circuits (c’est-à-dire du circuit d’antenne et du transformateur HF) correspondant à la fréquence f_s du signal que l’on désire recevoir, la fréquence de la composante de battement f_o – f_s gardera toujours la valeur de la fréquence intermédiaire c’est-à-dire 480kHz dans notre exemple.

Supposons, en effet, que nous désirions recevoir un signal dont la fréquence f_s = 1MHz = 1000kHz. En accordant le circuit d’antenne sur cette fréquence, la fréquence de l’oscillateur aura donc pour valeur 1000 + 480 = 1480kHz. La composante de battement f_o – f_s aura comme fréquence 1480 – 1000 = 480kHz

Les autres composantes du courant de collecteur auront des fréquences de : 1000kHz, 1480kHz, 2480kHz, égales respectivement à la fréquence f_s du signal reçu, à celle f_o de l’oscillateur et à celle du battement f_s + f_o.

De ces quatre composantes présentes dans le circuit du collecteur de TR₂, une seule vient à être amplifiée et précisément celle de 480 kH, parce que le circuit de collecteur de TR₂ est accordé sur cette fréquence.

De cette manière, le signal reçu (dont la fréquence est 1000kHz) après l’étage mélangeur, aura pour fréquence 480kHz. Vous voyez facilement en refaisant les calculs simples vus ci-dessus, que toute fréquence f_s sera convertie en une valeur fixe de 480kHz. Vous voyez aussi que si le signal reçu est modulé en amplitude, le signal à la sortie du mélangeur sera modulé de façon identique, puisque son amplitude variera proportionnellement à celle du signal reçu.

Le signal de fréquence intermédiaire conservera donc toutes les caractéristiques de la modulation du signal reçu et ne diffèrera de celui-ci que par la valeur de la fréquence porteuse.

Du secondaire L₇ du premier transformateur FI (dont le primaire accordé est constitué par C₆ et L₆), le signal à 480kHz passe dans les étages FI successifs.

2 – 2 CHANGEUR DE FRÉQUENCE AUTO-OSCILLANT

Dans les récepteurs portables, le circuit de la figure 3 est simplifié : l’amplificateur HF est supprimé et l’étage oscillateur et mélangeur est constitué par un seul transistor.

Ainsi un seul étage travaille comme changeur de fréquence, comme mélangeur et comme oscillateur. Le circuit est appelé "Convertisseur auto-oscillant" et son schéma est indiqué en figure 6.

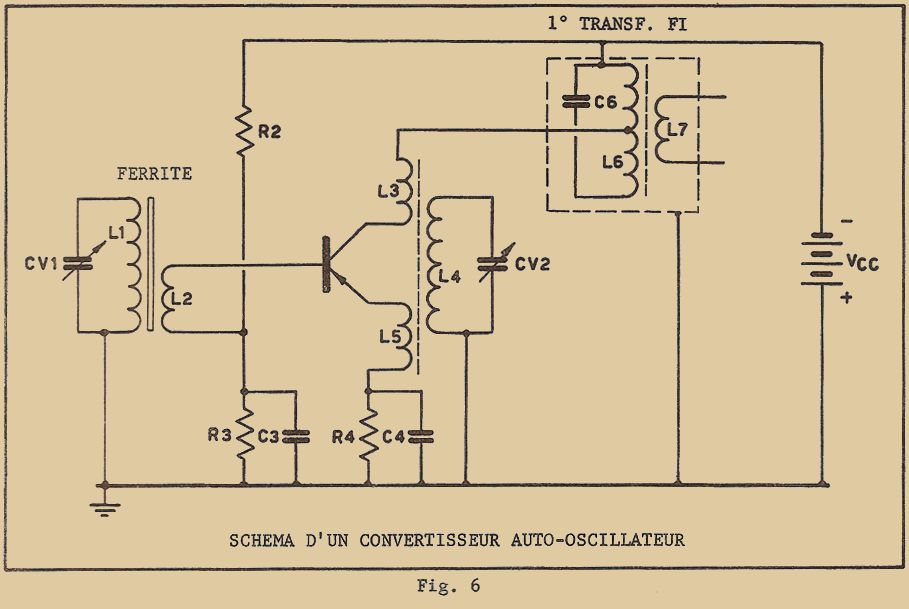
En examinant la figure 6, vous pouvez remarquer qu’étant donné que l’étage HF n’existe plus, le circuit d’antenne (toujours du type à ferrite quand il s’agit d’ondes longues et d’ondes moyennes) est directement relié à la base du changeur de fréquence.

Vous pouvez voir en comparant les schémas des figures 3 et 6 que ce dernier peut être considéré comme l’ensemble de l’oscillateur et du mélangeur de la figure 3. En effet, on retrouve le circuit de l’oscillateur (identique à celui de la figure 4 de la théorie 25) formé par le circuit résonnant L₄ et CV₂ auquel on vient coupler l’inductance L₃ de collecteur et L5 de réaction de l’émetteur.

De cette manière, le transistor fonctionne comme un oscillateur monté en base commune.

On retrouve encore le circuit mélangeur de la figure 3, constitué par le circuit d’entrée L₁ et CV₁ accordé sur la fréquence du signal reçu et couplé à la base du transistor par le secondaire L₂. Le couplage au premier transformateur FI est formé par C₆ et L₆ avec prise intermédiaire pour la liaison au collecteur. Le secondaire L₇ sert à la liaison avec l’étage suivant.

Le transistor fonctionne aussi comme mélangeur, de la même façon que le circuit de la figure 3 et se trouve monté en émetteur commun.

C’est le cas typique d’un transistor fonctionnant simultanément selon deux types de montage et accomplissant deux fonctions différentes.

L’utilisation du montage en émetteur commun pour accomplir la fonction de mélangeur et celle en base commune pour la fonction d’oscillateur permet au transistor de travailler simultanément sans qu’une fonction perturbe l’autre.

Le convertisseur auto-oscillant présente encore d’autres avantages par rapport à celui de l’oscillateur séparé. Les résultats sont pratiquement identiques dans les deux cas, et on fait l’économie d’un transistor.

Par contre, l’absence de l’étage HF amène obligatoirement le récepteur à être moins sensible et de sélectivité moindre, puisqu’il manque le circuit résonnant de transformateur de liaison entre TR₁ et TR₂ de la figure 3.

La simplification obtenue par l’intermédiaire de l’amplification HF (outre le fait qu’il y a un transistor en moins), permet encore d’utiliser un condensateur variable à deux cages seulement (CV₁ et CV₂ de la figure 6) beaucoup moins coûteux et encombrant que celui à trois cages de la figure 3.

En conclusion nous dirons que l’étage amplificateur HF donne une sensibilité élevée au récepteur (nécessaire par exemple dans le cas des auto-radios), et une forte atténuation de la fréquence-image comme nous allons le voir dans le chapitre suivant. Par contre le changeur de fréquence avec oscillateur séparé ne présente aucun avantage par rapport à celui auto-oscillant ; c’est un luxe inutile.

2 – 3 FRÉQUENCE-IMAGE

Nous avons examiné jusqu’à maintenant les aspects positif_s des circuits changeur de fréquence, c’est-à-dire les avantages que ceux-ci présentaient par rapport aux circuits classiques. Nous allons voir maintenant un aspect négatif, c’est-à-dire un inconvénient non négligeable et dont les conséquences peuvent être très importantes dans certains cas.

Rappelez-vous ce qui a été dit au sujet du mécanisme du changement de fréquence ; le signal à fréquence intermédiaire naît du battement entre le signal reçu f_s et le signal de fréquence f_o de l’oscillateur.

En général, pour des raisons pratiques, la fréquence de l’oscillateur est toujours supérieure à celle du signal reçu, mais ce n’est pas une condition impérative pour obtenir le changement de fréquence ; la fréquence de l’oscillateur peut être inférieure aussi à celle du signal.

La condition indispensable pour obtenir un signal de fréquence intermédiaire à 480kHz est que la différence entre f_s et f_o soit exactement de 480kHz et peu importe laquelle des deux fréquences est plus élevée.

Reprenons si vous le voulez bien, l’exemple de la réception d’un signal de 1MHz : pour plus de clarté, je vous l’ai illustré à la figure 7.

Si le récepteur est accordé pour recevoir un signal de 1MHz, le circuit d’entrée est accordé lui aussi sur cette fréquence (f_s = 1000kHz) et l’oscillateur sur une fréquence plus élevée de 480kHz (f_o = 1480kHz). Supposons maintenant, qu’il y ait un autre signal, de fréquence supérieure à f_o et qui soit plus élevée de 480kHz, c’est-à-dire que la fréquence de ce signal soit : 1480 + 480 = 1960kHz. Ce signal est indiqué par f_i sur la figure 7.

Comme nous l’avons vu précédemment, ce signal va battre avec l’oscillateur et donnera naissance à un signal de fréquence intermédiaire de 480kHz.

En effet, la différence entre les fréquences de ces signaux et celle de l’oscillateur sont respectivement :

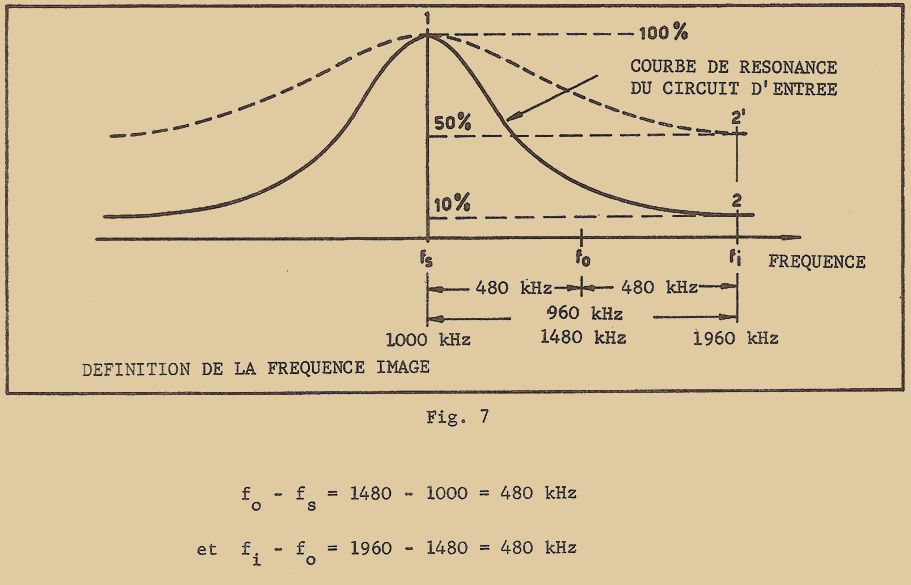
Les deux signaux vont être alors amplifiés simultanément par les amplificateurs FI qui suivent l’étage changeur de fréquence, et il n’y aura plus aucune possibilité de séparer les signaux puisqu’ils sont maintenant de même fréquence.

L’inconvénient dont je vous ai parlé tout à l’heure apparaît maintenant. Le changeur de fréquence ne peut séparer les deux signaux, qui se superposent et donnent une réception distordue soit par l'un, soit par l’autre.

En examinant la figure 7, nous pourrons affirmer ce qui suit : en accordant le récepteur sur une fréquence donnée f_s, on peut recevoir en plus un autre signal, de fréquence f_i supérieure à f_s exactement du double de la fréquence intermédiaire FI. Ce second signal prend le nom de signal image et sa fréquence est dite fréquence image.

Dans le cas des récepteurs dont la FI est de 480kHz comme cela arrive souvent, la fréquence image est toujours plus élevée que la fréquence d’accord de : 2 x 480 = 960kHz

Dans l’exemple considéré, on a en effet :

f_i = f_s + 960 = 1000 + 960 = 1960kHz (figure 7).

Pour éviter que le signal image interfère avec le signal que l’on désire recevoir, il faut lui interdire l’entrée du récepteur.

Pour éliminer le signal image, on ne peut jouer que sur les circuits sélectif_s qui précèdent le changeur de fréquence, c’est-à-dire sur le circuit résonnant d’antenne et sur celui (quand il existe) qui constitue le transformateur de liaison entre l’amplificateur HF et le changeur.

En effet, si le récepteur est accordé sur la fréquence f_s = 1000kHz comme nous l’avons supposé, le circuit d’entrée est accordé lui aussi sur cette fréquence et sa courbe de résonance peut être représentée avec le maximum en correspondance de f_s (figure 7).

Sur la même figure vous pouvez voir que le signal image tombe sur un flanc de la courbe de résonance (point 2) et que son amplitude résultante peut être plus ou moins réduite selon la forme de la courbe de résonance. Si le circuit d’entrée est très sélectif (courbe en traits pleins sur la figure 7), le signal f_i est très atténué : son amplitude se trouve réduite par exemple à 10%.

Si au contraire la sélectivité du circuit d’entrée est faible (courbe en pointillés sur la figure 7), le signal image se trouve peu atténué (point 2’) et pourra encore perturber fortement le signal que l’on désire recevoir en interférant avec lui.

Dans la gamme des petites ondes et encore plus dans celle des grandes ondes, les inconvénients de la fréquence image ne sont en réalité pas toujours aussi graves que l’on pourrait penser au premier abord.

Il suffit tout d’abord de penser qu’il n’y a pas forcément toujours, lorsque l’on désire recevoir un signal, un autre signal présent exactement sur la fréquence image ; et même si ce signal existe, il n’est pas du tout certain que son amplitude sera telle qu’elle perturbe le signal utile.

Dans ces gammes d’ondes, la fréquence image résultante est toujours très élevée par rapport à celle du signal (dans le cas de l’exemple, f_i est presque double de f_s). Dans la majorité des cas, la sélectivité du circuit d’antenne suffit pour réduire l’amplitude du signal image à des valeurs non dangereuses. Il suffit de faire un simple calcul pour établir que si le circuit d’antenne a un coefficient de qualité Q de 40 par exemple (ce qui peut être réalisé très facilement avec les antennes ferrite), le signal image se trouve réduit à un centième environ : on a obtenu ainsi une grande marge de sécurité contre les interférences.

Par contre, en onde courtes, les résultats sont un peu moins bons. En effet, plus la fréquence du signal reçu est élevée, plus la fréquence image est proche, et plus il est difficile de la séparer.

Supposons en effet que le signal à recevoir est de 10MHz. La fréquence-image est alors : 10 + 0960 = 10,960MHz, c’est-à-dire qu’elle est très près des 10MHz (figure 8).

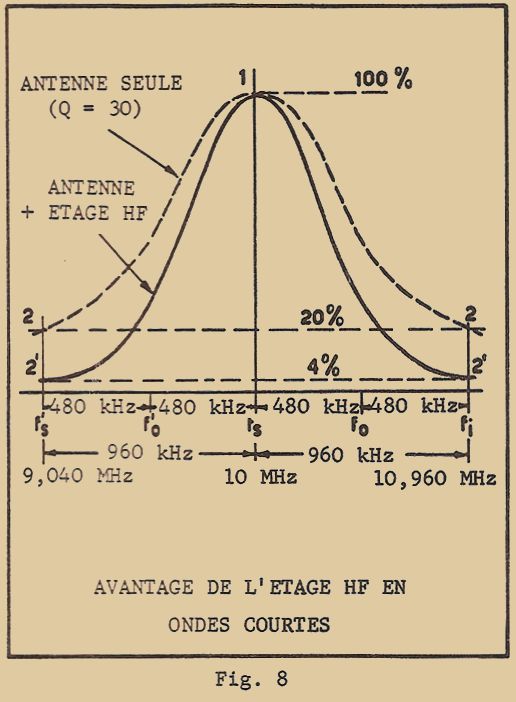
Si nous dessinons la courbe de résonance du seul circuit d’antenne (en supposant qu’il n’y a pas d’étage HF) et si nous supposons que la valeur de Q est de l’ordre de 30 (ce qui en pratique est facilement réalisable à ces fréquences) nous obtenons la courbe en pointillés de la figure 8. Nous voyons alors que le signal image est réduit à environ 20% par la sélectivité du circuit.

Si au contraire, il y a un étage HF et si nous admettons encore que le Q du circuit est de 30, la courbe résultante est celle qui est tracée en traits pleins (figure 8). Le signal image est alors réduit à 4% environ.

L’avantage d’un étage HF est évident par cet exemple : il y a réduction du signal image et une sensibilité plus grande du récepteur.

La réception du signal image, dans la gamme des ondes courtes en général (et dans quelques cas particuliers en petites ondes) donne lieu, outre à des interférences éventuelles, à la possibilité de recevoir le même signal, c’est-à-dire la même station, en deux points différents du cadran.

Il suffit en effet d’observer la figure 8, pour voir que le signal de fréquence f_s, peut être reçu, non seulement lorsque le récepteur est accordé sur cette fréquence, mais aussi quand il est accordé sur une fréquence f’s inférieure à f_s exactement du double de la valeur FI, c’est-à-dire de 960kHz. Dans ces conditions, le signal f_s est reçu comme signal image, étant donné que f_s se trouve distante de la fréquence f’o de l’oscillateur de 480kHz exactement et qu’elle se trouve convertie à la valeur précise de la FI.

CONCLUSION :

Le changement de fréquence a l’inconvénient de permettre la réception simultanée de deux stations (signal utile et signal image) ou, ce qui revient au même, permettre la réception de la même station en deux points du cadran distincts de 960kHz (si la FI = 480kHz) ou de 910kHz (si la FI = 455kHz).

Ces inconvénients ne peuvent être atténués que par la sélectivité des circuits qui précèdent le changeur ; pour cela, il faut choisir un circuit d’antenne dont le facteur de qualité Q soit suffisamment élevé ; quand cela n’est pas possible, il faut avoir recours à un étage amplificateur HF.

---

EXERCICES DE RÉVISION SUR LA 26^ème LEÇON THÉORIQUE

1 – En quoi consiste le changement de fréquence ?

2 – Quels sont les avantages que l’on obtient avec le changeur de fréquence ?

3 – De quel type est l’amplificateur HF ?

4 – Sur quel critère doit-on se baser pour choisir le point de fonctionnement du premier étage ?

5 – Qu’est le ferrite ?

6 – Quels sont les avantages de l’antenne magnétique (c’est-à-dire à ferrite) par rapport à l’antenne capacitive ?

7 – Comment obtient-on la fréquence intermédiaire ?

8 – Comment définit-on la fréquence image ?

9 – Comment peut-on réduire la réception du signal image ?

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 25^ème LEÇON THÉORIQUE

1 – On appelle oscillateur un circuit capable d’engendrer des oscillations.

2 – Il n’y a pas, à proprement parler de différence, entre un oscillateur BF et HF, à part la valeur de la fréquence. Les premiers sont du domaine acoustique, les autres des fréquences Radio.

3 – Un oscillateur est dit LC quand la fréquence des oscillations est déterminée par la résonance d’un circuit résonnant ; il est dit au contraire RC, quand la fréquence des oscillations est déterminée par un réseau, constitué uniquement de résistances et de capacités.

4 – On appelle réseau de réaction, le circuit qui sert à ramener le signal de sortie à l’entrée de l’étage.

5 - Un réseau de réaction fait en sorte de ramener le signal à l’entrée avec la phase et l’amplitude convenable, pour que l’étage puisse osciller.

6 – Quand le gain complexe de l’étage est supérieur à 1, le circuit est capable d’engendrer des oscillations.

7 – Un transistor utilisé en oscillateur base à la masse est capable d’engendrer des oscillations de fréquence beaucoup plus élevée qu’en montage émetteur à la masse.

8 – Dans le montage Hartley, le signal de réaction est obtenu en utilisant une self à prise intermédiaire ; dans le montage Colpitts on utilise au contraire deux capacités en série et une self sans prise.

9 – Un oscillateur RC à déphasage ne peut être réalisé en montage base à la masse, parce qu’avec un tel montage, on ne peut obtenir un gain en courant suffisant pour le fonctionnement d’un tel type d’oscillateur.

Fin de la leçon 26

---

LECON 27

AMPLIFICATEUR FI

Le signal à fréquence intermédiaire, prélevé à la sortie de l’étage changeur de fréquence que nous avons étudié dans la précédente leçon est appliqué à l’amplificateur FI de façon à pouvoir être amplifié énergiquement. Comme on a affaire à un signal qui est toujours de même fréquence (480kHz par exemple), il est évident que l’amplificateur FI sera du type sélectif à fréquence fixe, comme celui que nous avons étudié dans la 23ème leçon théorique.

Etant donné qu’en général un seul étage ne suffit pas à amener l’amplitude du signal à niveau convenable pour être détecté, l’amplificateur FI sera normalement constitué par deux étages identiques placés en cascade, couplés entr’eux et, au circuit détecteur qui les suit par l’intermédiaire de transformateurs accordés. Ces derniers pourront être du type à primaire seul accordé, ou bien à primaire et secondaire accordés.

Le schéma de principe d’un amplificateur FI pourra alors être du type de l’étage représenté en figure 9 de la théorique 24. Il sera constitué de deux étages en cascade.

Il va en résulter le schéma reporté en figure 1, où je vous ai représenté le primaire et le secondaire des transformateurs FI accordés tous les deux.

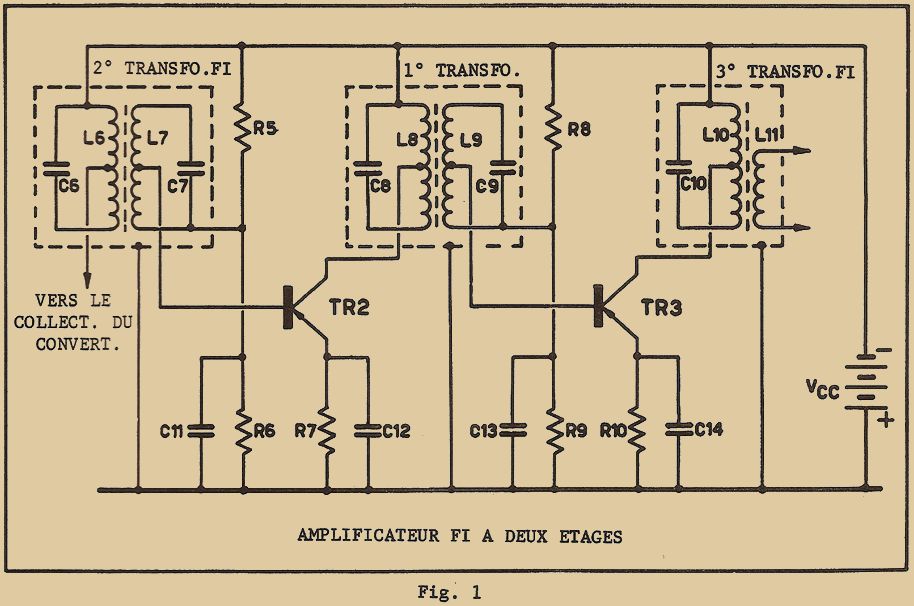
Le troisième transformateur FI a seulement son primaire accordé ; mais il est du même type que les deux premiers.

Comme nous l’avons vu en son temps (théoriques 23 et 24), le fait d’avoir les secondaires accordés confère au récepteur une meilleure sélectivité, c’est-à-dire une aptitude meilleure à séparer entr’elles deux stations voisines ; mais ceci entraine des transformateurs plus coûteux. C’est ainsi que les récepteurs du type portable n’ont en général que le primaire accordé.

Le premier transformateur FI sert à relier l’étage changeur de fréquences au premier étage amplificateur FI constitué par le transistor TR₂. La prise intermédiaire de ce transformateur est reliée à la sortie du transistor qui fonctionne comme changeur de fréquences.

Le premier transformateur FI, représenté en figure 1, est le même que celui qui a été représenté en figures 3 et 6 de la leçon théorique 25.

Les étages FI sont composés des transistors TR₂ et TR₃ montés en émetteur à la masse. Ils sont polarisés et stabilisés du point de vue thermique par l’intermédiaire respectivement des résistances R₇ et R₁₀. Les bases sont polarisées à l’aide des ponts de résistances R₅ et R₆ pour TR₂ et R₈ – R₉ pour TR₃ ; les polarisations se font à travers les enroulements secondaires L₇ et L₉ des transformateurs de liaison.

Les condensateurs C11, C12, C13 et C14 servent comme à l’habitude à supprimer les effets de contre-réaction des circuits de polarisation sur les signaux FI.

Du secondaire L11 du troisième transformateur FI on prélève le signal FI amplifié, pour l’appliquer au circuit détecteur non représenté en figure 1.

Selon le type des transistors utilisés, le schéma de la figure 1 peut encore être complété par des circuits de neutrodynage (non dessinés sur la figure) comme nous l’avons vu dans la théorie 24.

Les points de fonctionnement de TR₂ et TR₃ sont choisis encore en se basant sur la notion du "bruit de fond" : en général ils sont choisis pour que les courants de collecteur soient de l’ordre de 0,5 à 1mA.

Les transformateurs FI sont toujours enfermés dans des boitiers métalliques (indiqués par des rectangles en pointillés sur la figure 1) qui sont réunis à la masse. La réalisation pratique des transformateurs est faite selon l’un des deux schémas illustrés en figure 5 de la théorique 24.

1 – 1 CIRCUIT DE DÉTECTION

A la sortie de l’amplificateur FI, le signal a une amplitude de l’ordre de 0,5V à 1V (ou même plus) selon l’intensité du signal reçu et une fréquence de 480kHz quelle que soit la fréquence du signal reçu : mais ce signal sera toujours constitué par une porteuse (à 480kHz) modulée en amplitude exactement comme le signal capté par l’antenne.

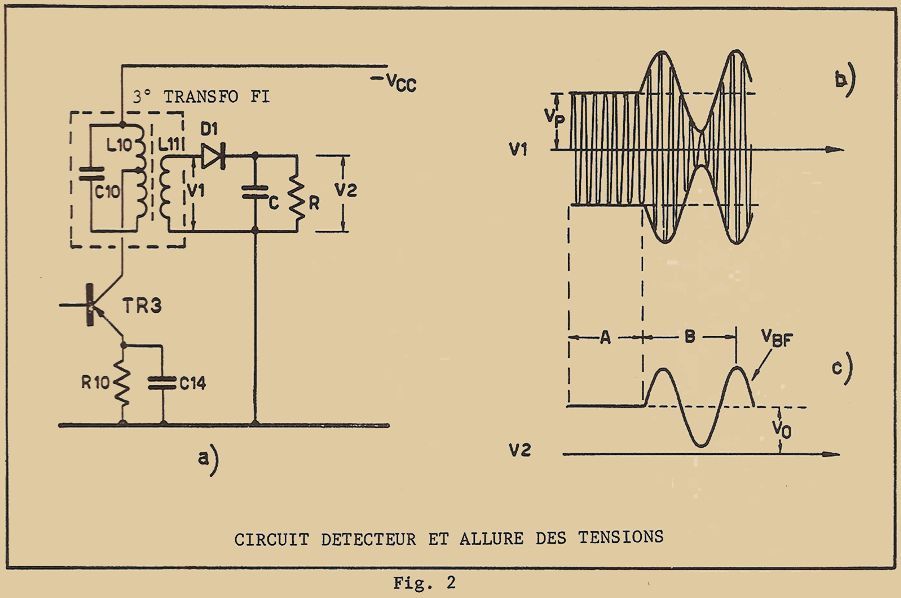
Pour obtenir le signal de basse fréquence, c’est-à-dire celui qui constitue "l’information" transmise (ou en d’autre termes, le signal qui a été utilisé pour moduler la porteuse), il faut démoduler le signal FI à l’aide d’un circuit détecteur (ou démodulateur).

Ce dernier est constitué comme on peut le voir en figure 2a, par une diode dite Diode de détection (ou détecteur) et par un condensateur et une résistance placés en parallèle et formant le circuit RC de détection ; la diode et l’ensemble RC, sont placés en série et sont reliés directement aux bornes du secondaire L11 du dernier transformateur FI.

Pour étudier le comportement du circuit détecteur, il faut avant tout considérer l’allure du signal qu’on lui applique, c’est-à-dire la forme du signal que l’on trouve à la sortie de l’amplificateur FI. Celui-ci, comme nous l’avons déjà vu, est constitué par une porteuse à 480kHz, modulée en amplitude. Cette porteuse est représentée par une onde sinusoïdale dont l’amplitude reste constante en l’absence de modulation (région A de la figure 2b) et qui varie autour de cette valeur quand elle est modulée (comme par exemple dans la région B (figure 2b). Dans ce dessin pour simplifier j’ai considéré que la modulation était sinusoïdale.

Comme la diode ne conduit que lorsque son anode est positive par rapport à la cathode, il est évident qu’elle ne laissera passer que l’alternance positive du signal à fréquence intermédiaire, et chargera le condensateur C à la valeur de crête. La tension aux bornes de C aura donc comme valeur V_c égale à la valeur de crête V_p de l’alternance positive.

Dans la région A de la figure 2b, la tension V_c reste de valeur constante, parce que l’amplitude des crêtes du signal FI est elle-même constante. Dans la région B par contre, la tension aux bornes de C augmente et diminue autour de cette valeur en suivant l’allure de la modulation.

Aux bornes de C, ou mieux, aux bornes du circuit de détection RC, nous avons un signal qui peut être considéré comme composé d’une composante continue Vo (figure 2c) de valeur constante et égale à la valeur de crête de la porteuse non modulée à laquelle vient se superposer une composante alternative qui est l’enveloppe de la modulation et qui constitue à proprement parler le signal basse fréquence, indiqué VBF sur la même figure.

En réalité le phénomène de la détection est plus compliqué en ce sens qu’il faut encore tenir compte du comportement du circuit de détection dans l’intervalle de temps qui s’écoule entre une alternance positive et la suivante.

Il est bon de se rappeler brièvement comment se fait la décharge d’un condensateur sur une résistance. Considérons pour cela le circuit de la figure 3a lorsque l’on ferme l’interrupteur S, le condensateur C se trouve branché directement aux bornes de la pile et se trouve donc chargé à la tension de cette dernière. Supposons que la pile ait une tension V_cc de 10 V : la tension V_c aux bornes du condensateur sera donc de 10V.

Ouvrons maintenant l’interrupteur : le condensateur va commencer par se décharger dans la résistance R et la tension V_c à ses bornes va diminuer.

Au fur et à mesure que le condensateur se décharge, la tension V_c (qui est aussi la tension aux bornes de R, puisque Ret C sont en parallèle) diminue et suit l’allure représentée en figure 3b.

La tension V_c décroît d’abord très rapidement, puis toujours de plus en plus lentement et tend graduellement à s’annuler. On démontre que l’allure de la tension V_c suit une loi bien déterminée, que les mathématiciens appellent "exponentielle" : c’est pour cette raison que l’on dit que la tension suit une "loi exponentielle".

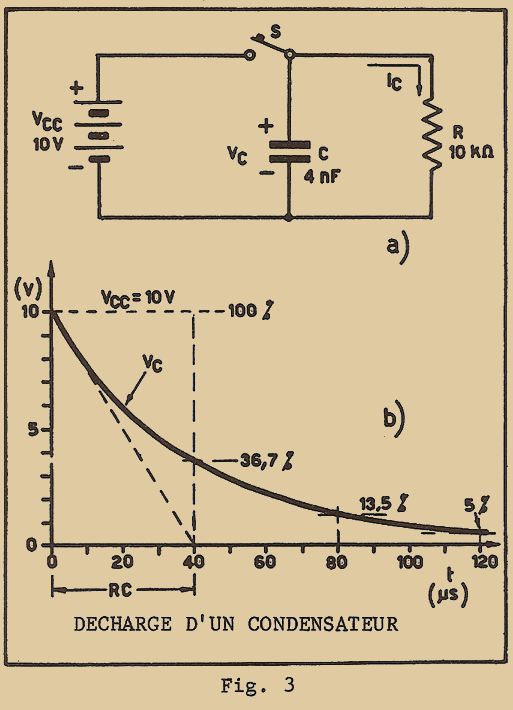
Par intuition, on "sent" que la décharge du condensateur sera d’autant plus rapide que la capacité est plus faible, parce que la charge accumulée est elle-même faible, ou bien que la résistance est plus petite, parce qu’alors le courant de décharge du condensateur est plus grand.

D’une façon plus exacte, la décharge dépend du produit de la valeur de C par la valeur de R, produit qui prend le nom de constante de temps : si l’on exprime C en nF et R en kΩ, le produit RC sera donné enµS (microsecondes, c’est-à-dire en millionième de seconde). Par exemple, si C = 4 nF et R= 10kΩ, on aura RC = 4 x 10 = 40µS.

La valeur de la constante de temps RC détermine exactement la décharge du condensateur, en ce sens que dans chaque intervalle de temps égal à la valeur RC, la tension aux bornes de C diminue de 2,72 fois. Ainsi dans le cas de l’exemple, comme RC = 40µS, la tension aux bornes de C part de la valeur de 10V et se réduira à la valeur de 10 / 2,72 = 3,67V au bout d’un temps égal à la valeur de RC, c’est-à-dire en 40µS. Au bout d’un autre temps de 40µS, la tension va encore diminuer de 2,72 fois et deviendra : 3,67 / 2,72 = 1,35V et ainsi de suite.

D’une façon plus générale, nous dirons que la tension V_c part d’une valeur de charge égale à 100% et se réduit à 100 / 2,72 = 36,7% de sa valeur en un intervalle de temps égal à RC. Dans un second intervalle de temps égal à RC, la tension se réduit à 36,7 / 2,72 = 13,5% de sa valeur primitive. Après un troisième intervalle de temps égal à RC, la tension est devenue : 13,5 / 2,72 = 5% de ce qu’elle était au départ, et ainsi de suite.

Le courant qui traverse la résistance suit une loi semblable ; quand l’interrupteur est fermé, le courant est :

V_cc / R=10V / 10kΩ = 1mA.

Ensuite, il décroit en suivant une loi semblable à celle de la tension V_c lorsque l’on a ouvert l’interrupteur.

Après cette parenthèse sur le comportement de la décharge du condensateur, nous pouvons revenir au circuit de détection de la figure 2a.

Nous remplacerons seulement la pile de la figure 3a par le secondaire du transformateur FI qui délivre une tension alternative à la fréquence de 480kHz.

La diode pourra être assimilée à un interrupteur qui est fermé quand la diode conduit, c’est-à-dire lorsque l’anode est positive par rapport à la cathode, et ouvert quand l’anode est négative par rapport à la cathode. En première approximation, nous pourrons donc dire que la diode se comporte comme un interrupteur fermé pendant l’alternance positive et comme un interrupteur ouvert pendant l’alternance négative.

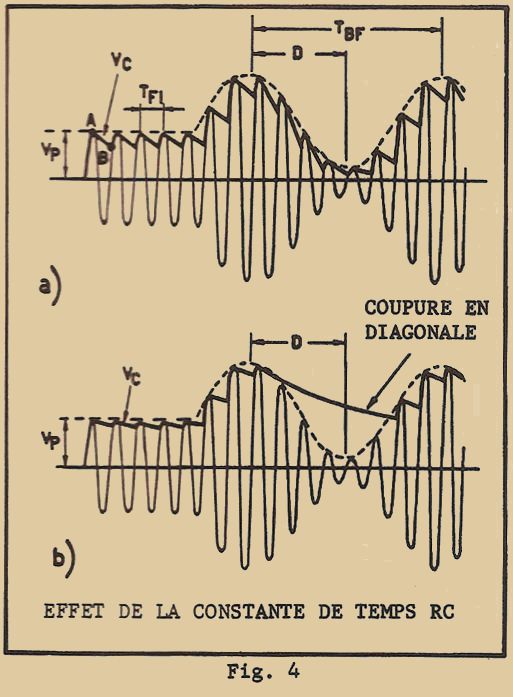
Si l’on considère alors la tension délivrée par L11 et appliquée à l’anode de la diode (je vous refais le dessin de la figure 2b à la figure 4a), on peut dire que pendant l’alternance positive, la diode conduit et le condensateur se charge à la valeur de crête V_p quand l’alternance atteint sa valeur maximum.

A partir ce cet instant (A sur la figure 4a), la tension appliquée sur l’anode diminue rapidement en suivant une loi sinusoïdale, tandis que la tension aux bornes du condensateur diminue plus lentement en suivant une loi exponentielle que nous venons de voir.

Comme la tension aux bornes de C est celle-là même qui se trouve sur la cathode de la diode, vous voyez que la tension sur la cathode est positive et plus élevée que celle qui se trouve sur l’anode : pour cette raison, la diode ne conduit plus et le circuit se comporte comme celui de la figure 3a quand l’interrupteur a été ouvert.

La décharge de C va se produire jusqu’à l’instant B (figure 4a) : à cet instant la tension appliquée sur l’anode de la diode va se trouver de nouveau légèrement plus élevée que celle sur la cathode ; la diode va conduire à nouveau et va recharger C à la valeur de crête de la tension FI. Le phénomène va se répéter à chaque cycle de la fréquence intermédiaire ; la tension aux bornes du circuit RC va donc se présenter en dents de scie (ligne dessinée en gras sur la figure 4a), et suivant aussi l’enveloppe de la modulation.

L’amplitude de la "dentelure" dépend évidemment de la proportion dont se décharge le condensateur dans l’intervalle de temps qui s’écoule entre une alternance et l’autre ; elle est d’autant moins grande que le condensateur se décharge moins, c’est-à-dire que la constante de temps du circuit de détection RC est elle-même plus grande.

Pour obtenir ainsi une tension détectée qui suit parfaitement l’allure de l’enveloppe de modulation, comme indiqué en figure 2c, il s’agit de choisir une constante de temps élevée, c’est-à-dire très grande par rapport à l’intervalle de temps qui s’écoule entre deux crêtes successives de la tension FI ; cet intervalle de temps n’est autre que la période de la fréquence intermédiaire, dont la valeur est :

T_FI = 1/f_FI = 1/0,480 = 2,08µS

La constante de temps du circuit RC ne peut toutefois être rendue trop grande : sinon un phénomène particulier apparait.

Considérons la région D (figure 4a) où l’enveloppe de la modulation décroît rapidement ; si le condensateur se décharge trop lentement, il peut arriver que la tension aux bornes du circuit RC, au lieu de suivre l’enveloppe de modulation comme en figure 4a, décroisse comme en figure 4b.

Dans ce cas, la tension détectée est loin d’avoir la forme de l’enveloppe ce qui indique que la tension basse fréquence résultante est distordue. Ce type de distorsion est appelé "distorsion en diagonale".

Pour éviter cet inconvénient, il faut encore que la constante de temps du circuit de détection soit petite par rapport à l’intervalle de temps qui s’écoule entre deux crêtes successives de l’enveloppe de modulation.

Cet intervalle de temps n’est autre que la période de la fréquence de modulation. Il faut donc prendre en considération la période de la fréquence maximum de modulation que l’on désire transmettre.

Dans le cas des transmissions en modulation d’amplitude, la valeur maximum de la fréquence est de 4,5kHz ; la valeur de T_BF à considérer est :

T_BF = 1/(4,5kHz) = 0,222mS = 222µS

Pour un bon détecteur, la valeur de la constante de temps devra donc être beaucoup plus grande que 2,08µS pour réduire la dentelure, et beaucoup plus faible que 222µS pour éviter la distorsion. En pratique on prend pour RC une valeur comprise entre 20µS et 60µS. En prenant par exemple, une constante de temps de 50µS, celle-ci pourra être réalisée en prenant C = 10 nF et R= 5kΩ.

On démontre encore que le circuit de détection se comporte, vis-à-vis du transformateur FI, comme une charge dont la valeur est égale à R/2 ; ainsi dans l’exemple précédent où Rétait égale à 10kΩ, le rapport de transformation du transformateur FI devra être calculé comme si l’on devait charger le secondaire L11 par une résistance de 10/2 = 5kΩ.

Le signal présent à la sortie du détecteur se partage en ses deux composantes : la composante alternative est envoyée vers les étages basse fréquence ; la composante continue dont l’amplitude est proportionnelle à l’amplitude du signal HF reçu (elle est en effet égale à l’amplitude de crête de la porteuse non modulée) sert pour le circuit RAS (régulateur automatique de sensibilité) que nous allons voir maintenant.

La séparation des deux composantes peut être faite très simplement à l’aide des circuits représentés en figure 5.

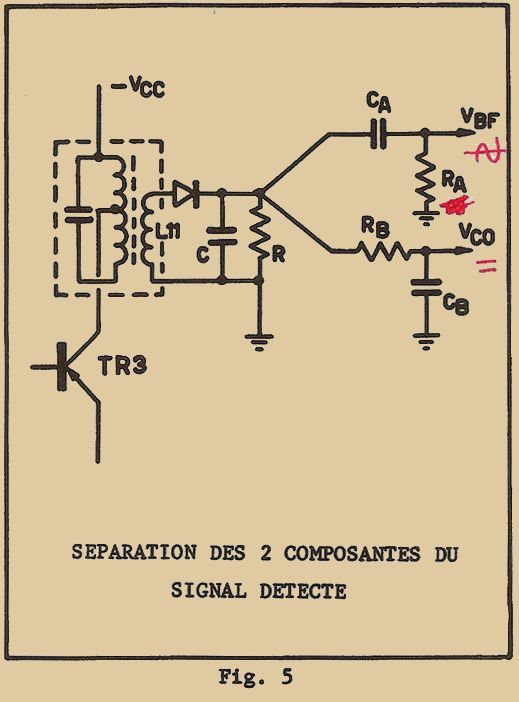
Pour obtenir seulement la composante alternative, on peut en effet bloquer la composante continue par une liaison RC, comme dans le cas des liaisons entre étages des amplificateurs. Le condensateur C_A va bloquer en effet, la composante continue et aux bornes de R_A on ne trouvera plus que la composante alternative, c’est-à-dire le signal de basse fréquence.

Pour éliminer au contraire la composante alternative et récupérer uniquement la seule composante continue, il suffit d’utiliser le circuit R_B C_B.

De cette manière, le condensateur va se comporter comme un filtre de nivellement et rendra la tension à ses bornes constante c’est-à-dire insensible aux variations dûes à la modulation, se comportant de la même manière que le condensateur d’émetteur d’un transistor qui rend la tension de polarisation constante.

1 – 2 CIRCUIT RAS

Le circuit RAS, comme nous l’avons déjà vu, a pour rôle de régler de façon tout à fait automatique la sensibilité du récepteur en se basant sur l’intensité du signal reçu, de façon qu’il soit très sensible lors d’une réception faible et peu sensible en présence d’un signal fort.

On a ainsi l’avantage d’avoir à la sortie du détecteur un signal qui reste pratiquement constant quand on passe d’une station forte à une faible. Ainsi, le volume sonore reste constant quand on écoute une station dont l’intensité varie pour des raisons de propagation, comme le fameux phénomène dit de "fading" propre à la propagation ionosphérique et qui est typique dans les transmissions en ondes courtes.

Un autre avantage du RAS est d’éviter qu’avec des signaux forts, on ne sature le dernier étage FI : l’enveloppe de modulation serait distordue avec comme conséquence une distorsion du signal basse fréquence.

Le réglage de la sensibilité du récepteur se fait en agissant sur le gain du premier étage FI et sur celui de l’étage HF quand ce dernier existe. Pour ce réglage, on exploite la composante continue délivrée par le détecteur (qui comme nous l’avons vue, est d’autant plus grande que le signal reçu est plus intense).

Le schéma le plus simple d’un circuit RAS est indiqué en figure 6.

La résistance R₆ du pont de résistances de polarisation de la base de TR₂ est branchée à la sortie du détecteur au lieu d’être reliée à la masse comme sur la figure 1. De cette manière, la tension de polarisation de la base de TR₂ dépend aussi de la composante continue délivrée par le détecteur.

En l’absence de signal, TR₂ est polarisé normalement : en présence d’un signal au contraire, le point A (sortie du détecteur de la figure 6) devient positif par rapport à la masse et, en conséquence, le point B (auquel est reliée la base de TR₂ à travers le secondaire L 7) devient moins négatif.

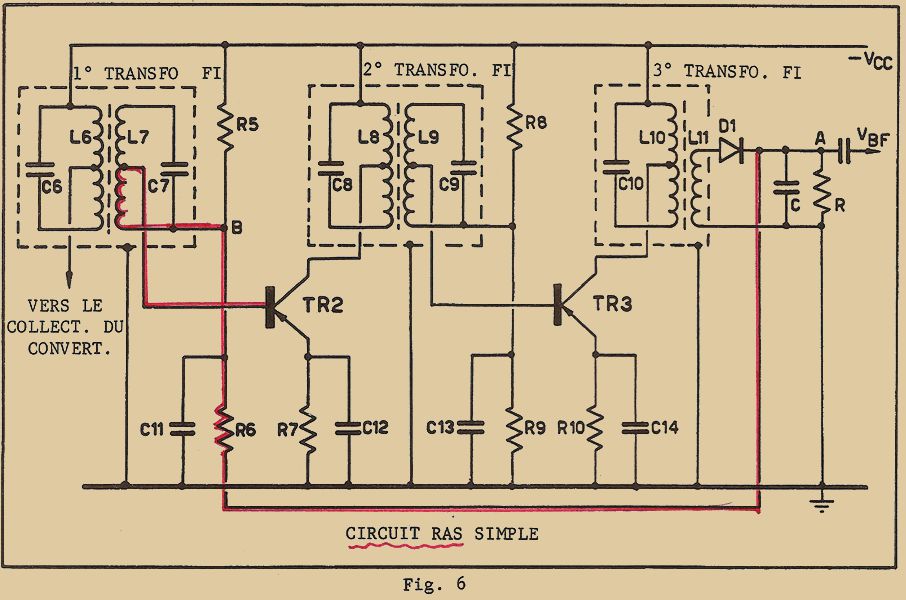
Ceci correspond à une réduction du courant de polarisation de la base de TR₂, réduction qui est d’autant plus forte que la tension positive est plus grande, c’est-à-dire que le signal reçu est plus intense.

La réduction du courant de polarisation de la base comporte une réduction du courant du collecteur, c’est-à-dire une variation des paramètres du transistor. Si, en l’absence du signal, le transistor travaille dans des conditions de gain maximum, il est évident qu’une variation quelconque de ces conditions a pour effet de réduire le gain.

En comparant le circuit de la figure 6 avec celui de la figure 5, on peut remarquer que la fonction de filtrage accomplie précédemment par R_B C_B est maintenant réalisée par la résistance R₆ elle-même et le condensateur C 11.

Le circuit de la figure 6 n’est pas très efficace et on pourrait penser l’améliorer en faisant agir aussi le RAS sur TR₃. Mais ce système n’est pas utilisé en général, pour éviter qu’avec de forts signaux, c’est-à-dire quand les transistors sont amenés à travailler avec de faibles courants de collecteur et très près du cut-off, TR₃ ne puisse distordre le signal qu’on lui applique car celui-ci est déjà d’une amplitude notable.

Une amélioration du circuit est cependant obtenue en modifiant ultérieurement le schéma comme indiqué en figure 7 ; on ajoute une diode D2 qui prend le nom de diode d’amortissement et dont le fonctionnement est le suivant.

En l’absence de signal, le courant de collecteur de TR₂ est fort, ainsi que la chute de tension aux bornes de R₁₂ (si par exemple elle est de 2V et que V_cc = 9V, la tension au point M sera de 7 V).

Dans ces conditions, en choisissant convenablement la valeur de R₁₁ on peut obtenir aux bornes de celle-ci une chute de tension qui serait par exemple seulement de 1V, c’est-à-dire que la tension du collecteur de TR₁ (ainsi que le point N) serait de 8V.

La diode, branchée avec son anode au point N et sa cathode au point M, a son anode à – 8V, tandis que la cathode se trouve à – 7V. La polarisation de la diode est donc telle que l’anode est plus négative que la cathode ; la diode est donc bloquée, elle se comporte comme un interrupteur ouvert et n’a aucune influence sur le fonctionnement du circuit.

Si maintenant on reçoit un signal, comme nous l’avons vu dans le schéma de la figure 6, le courant de TR₂ diminue : la chute de tension aux bornes de R₁₂ diminue aussi et le point M monte vers des valeurs négatives plus élevées (devient plus négatif), tandis que la tension au point N reste toujours à la même valeur, car le courant de TR₁ n’est pas contrôlé par le circuit RAS.

Lorsque l’intensité du signal reçu augmente, la tension du point M augmente aussi, c’est-à-dire la tension de la cathode de la diode. Dès que la valeur de la tension de la cathode atteint celle de l’anode, la diode commence à conduire (la cathode devient en effet plus négative que l’anode). La diode se comporte alors comme une résistance de valeur d’autant plus faible que la tension de la cathode est plus grande, c’est-à-dire que le signal reçu est plus intense.

Comme la diode se trouve branchée, en ce qui concerne la composante alternative du signal amplifié par TR₁, en parallèle sur le circuit résonnant L 6 – C 6 celui-ci sera amorti d’autant plus que l’intensité du signal reçu sera plus forte : ainsi le gain de l’étage se trouvera d’autant plus réduit.

L’action de la diode d’amortissement s’ajoute à celle obtenue directement avec TR₂ qui se comporte de la même manière que précédemment (cas du schéma de la figure 6). Le circuit de la figure 7 se trouve être beaucoup plus efficace que précédemment, mais en revanche il est plus complexe et plus onéreux.

Nous en avons ainsi terminé avec l’étude des amplificateurs FI et des circuits de commande automatique de sensibilité (CAS ou RAS). Nous commencerons dans la prochaine leçon l’étude des circuits amplificateurs à basse fréquence.

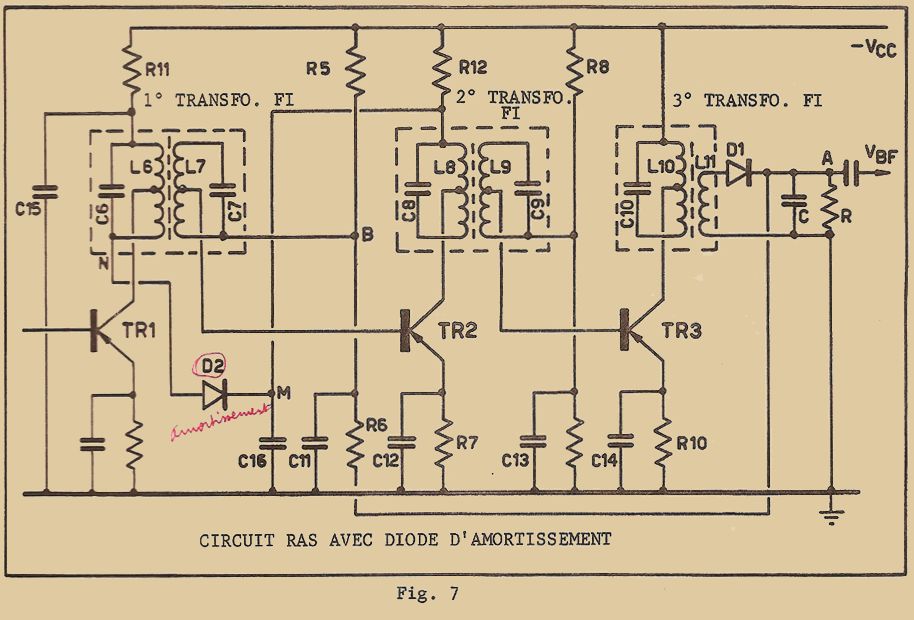
Dans ces conditions, en choisissant convenablement la valeur de R₁₁ on peut obtenir aux bornes de celle-ci une chute de tension qui serait par exemple seulement de 1V, c’est-à-dire que la tension du collecteur de TR₁ (ainsi que le point N) serait de 8V.

La diode, branchée avec son anode au point N et sa cathode au point M, a son anode à – 8V, tandis que la cathode se trouve à – 7V. La polarisation de la diode est donc telle que l’anode est plus négative que la cathode ; la diode est donc bloquée, elle se comporte comme un interrupteur ouvert et n’a aucune influence sur le fonctionnement du circuit.

Si maintenant on reçoit un signal, comme nous l’avons vu dans le schéma de la figure 6, le courant de TR₂ diminue : la chute de tension aux bornes de R₁₂ diminue aussi et le point M monte vers des valeurs négatives plus élevées (devient plus négatif), tandis que la tension au point N reste toujours à la même valeur, car le courant de TR₁ n’est pas contrôlé par le circuit RAS.

Lorsque l’intensité du signal reçu augmente, la tension du point M augmente aussi, c’est-à-dire la tension de la cathode de la diode. Dès que la valeur de la tension de la cathode atteint celle de l’anode, la diode commence à conduire (la cathode devient en effet plus négative que l’anode). La diode se comporte alors comme une résistance de valeur d’autant plus faible que la tension de la cathode est plus grande, c’est-à-dire que le signal reçu est plus intense.

Comme la diode se trouve branchée, en ce qui concerne la composante alternative du signal amplifié par TR₁, en parallèle sur le circuit résonnant L 6 – C 6 celui-ci sera amorti d’autant plus que l’intensité du signal reçu sera plus forte : ainsi le gain de l’étage se trouvera d’autant plus réduit.

L’action de la diode d’amortissement s’ajoute à celle obtenue directement avec TR₂ qui se comporte de la même manière que précédemment (cas du schéma de la figure 6). Le circuit de la figure 7 se trouve être beaucoup plus efficace que précédemment, mais en revanche il est plus complexe et plus onéreux.

Nous en avons ainsi terminé avec l’étude des amplificateurs FI et des circuits de commande automatique de sensibilité (CAS ou RAS). Nous commencerons dans la prochaine leçon l’étude des circuits amplificateurs à basse fréquence.

---

EXERCICES DE RÉVISION SUR LA 27^ème LEÇON THÉORIQUE

1 – Quel est le type de l’amplificateur FI ?

2 – Quelle sorte de signal le détecteur délivre-t-il ?

3 – Par quoi est donnée la constante de temps d’un circuit RC ?

4 – Qu’exprime la constante de temps RC ?

5 – Calculer la constante de temps d’un circuit RC où R= 1 MΩ et C = 250 pF.

6 – A quoi sert le RAS ?

7 – A quelle tension se charge le condensateur du circuit de détection en l’absence de modulation ?

8 – Quelle doit être la polarité de la tension RAS dans un récepteur à transistors ?

9 – Lorsqu’un condensateur C se décharge dans une résistance quelle est la valeur de la tension atteinte au bout d’un intervalle de temps égal à la constante de temps ?

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 26^ème LEÇON THÉORIQUE

1 – Le changement de fréquence consiste à convertir la fréquence du signal reçu, quel qu’il soit, en une valeur fixe de 480kHz (par exemple).

2 – Les avantages du changement de fréquence résident en une plus grande simplicité des circuits des récepteurs et dans une meilleure sélectivité obtenue.

3 – L’amplificateur HF est du type sélectif et à accord variable.

4 – Le point de fonctionnement du premier étage est choisi de façon à ce que le "bruit de fond" produit par le transistor soit le plus faible possible.

5 – Le ferrite est un matériau céramique dont les qualités magnétiques restent bonnes même aux fréquences élevées ; de plus il n’est pas conducteur.

6 – L’antenne magnétique (à ferrite) est plus avantageuse par rapport à l’antenne capacitive parce qu’elle est moins sensibles aux parasites.

7 – La fréquence intermédiaire est donnée par la différence entre la fréquence du signal reçu et celle de l’oscillateur.

8 – On appelle fréquence-image, la fréquence qui diffère de la fréquence d’accord (et lui est supérieure) du double de la valeur de la fréquence intermédiaire.

9 – Le signal-image ne peut être réduit que par des circuits sélectifs qui précèdent le changeur de fréquence.

Fin de la leçon 27

---

LECON 28

CIRCUITS AMPLIFICATEURS A BASSE FRÉQUENCE

Nous avons déjà étudié les amplificateurs basse fréquence dans les cours théoriques 17 à 22 ; nous n'avons donc pas besoin de les réétudier.

Nous allons examiner seulement comment ils s’insèrent dans le circuit général du récepteur.

Un schéma type de la partie basse fréquence d’un récepteur peut être celui indiqué en figure 1. Vous pouvez y voir un premier étage préamplificateur couplé capacitivement à un second étage, qui délivre une puissance suffisante pour commander l’étage final qui est en général du type push-pull fonctionnant en classe AB.

Ces différents étages sont en tout point identiques à ceux que nous avons étudiés séparément dans les leçons précédentes. La seule nouveauté réside dans les contrôles manuels de volume et de tonalité.

Le contrôle manuel de volume sert au réglage du volume sonore de la parole ou de la musique reproduites dans le haut-parleur. Il est en général constitué par un potentiomètre (P1 de la figure 1) à l’aide duquel on vient prélever une fraction plus ou moins grande du signal basse fréquence délivré par le détecteur.

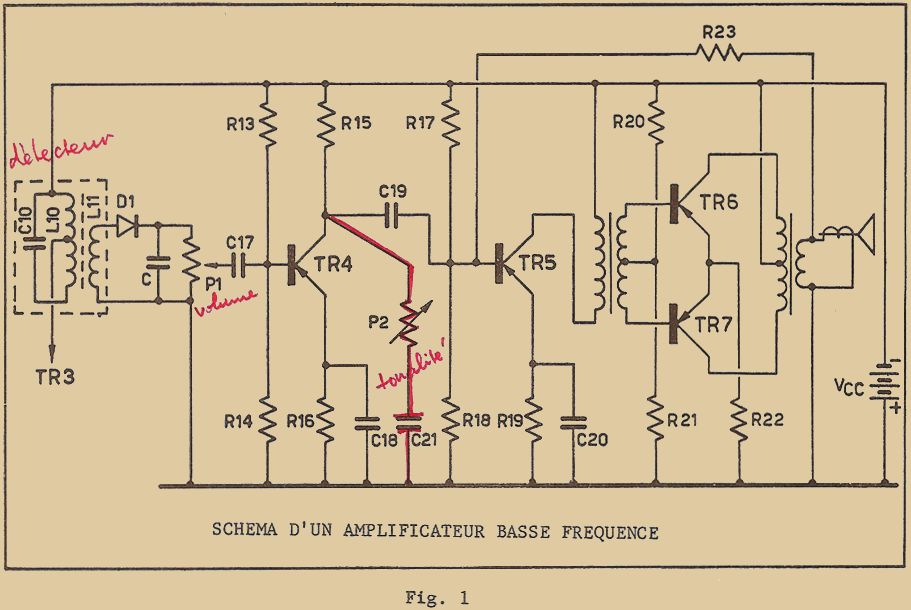
En effet, comme on peut le voir d’après le schéma de la figure 1, quand le curseur de P₁ se trouve en position haute, toute la tension présente aux bornes du potentiomètre (c’est-à-dire toute la tension délivrée par le détecteur) est appliquée sur la base de TR₄ et on obtient ainsi un volume sonore maximum.

En déplaçant le curseur vers le bas, la tension appliqué sur la base de TR₄ se trouve de plus en plus réduite et s’annule complètement quand le curseur de P₁ se trouve en position basse (minimum de volume).

Le contrôle de tonalité s’effectue en général à la sortie de l’étage préamplificateur (TR₄ de la figure 1) et comme je l’ai déjà dit, agit sur la bande passante de l’amplificateur basse fréquence.

Le type le plus couramment utilisé agit seulement sur les fréquences élevées, c’est-à-dire sur la fréquence de coupure supérieure de l’amplificateur ; s’il est du type à réglage continu, il peut être réalisé à l’aide d’un potentiomètre en série avec un condensateur (P₂ et C₂₁ de la figure 1) branchés entre le collecteur du transistor et la masse.

Le fonctionnement en est très simple. Quand le potentiomètre est tourné du côté de la résistance minimum, le condensateur se trouve branché directement entre le collecteur et la masse. La fréquence de coupure supérieure est alors réduite à une certaine valeur, déterminée par la capacité C₂₁ (revoir la leçon théorique 22). Dans ces conditions, les fréquences élevées subissent une certaine atténuation et la reproduction sonore est plus ou moins sourde.

En tournant au contraire P₂ de façon que sa résistance soit maximum, l’action de C₂₁ est pratiquement annulé ; et le circuit se comporte comme si C₂₁ n’existait pas. La fréquence de coupure supérieure reprend sa valeur maximum, définie par les caractéristiques des transistors utilisés. Dans ces conditions, les fréquences élevées ne sont pas atténuées et la reproduction se fait dans toute la gamme des fréquences acoustiques.

Il est évident d’autre part, qu’en tournant l’axe du potentiomètre sur des positions intermédiaires, l’action de C₂₁ sera plus ou moins limitée et qu’ainsi la fréquence de coupure supérieure pourra être réglée à volonté entre les valeurs maximum et minimum indiquées ci-dessus. Les fréquences élevées seront atténuées d’une manière plus ou moins prononcée.

Le contrôle de tonalité, au lieu d’être continu peut aussi être réalisé sous une forme "par bonds". On peut même le réaliser sous la forme extrême à deux possibilités seulement : atténuation maximum ou nulle. Dans ce cas, le potentiomètre P₂ est remplacé par un interrupteur qui met en service ou hors service, C₂₁ en le reliant ou non au collecteur de TR₄.

D’autres circuits plus complexes peuvent aussi être réalisés pour contrôler l’atténuation ou l’expansion des fréquences basses. Etant donné, qu’ils ne sont pas en général utilisés dans les récepteurs radio, mais seulement dans des chaines à haute fidélité (Hi-Fi), nous ne les traiterons pas dans cette leçon.

1 – 1 CONTRE-RÉACTION OU RÉACTION NÉGATIVE

Nous allons considérer un amplificateur, qui a un certain gain en courant (par exemple G_i = 100) et qui alimente une certaine charge R_c (par exemple un haut-parleur).

A l’aide d’un générateur, relié aux bornes d’entrée de l’amplificateur (figure 2a), nous allons injecter un signal de commande, constitué par le courant ie.

En agissant sur le potentiomètre P, nous pouvons régler la valeur du courant de commande qui attaque l’amplificateur au travers de la résistance R de forte valeur (cette valeur élevée est nécessaire précisément pour obtenir une commande en courant comme nous l’avons vu précédemment).

Réglons donc le potentiomètre pour avoir un courant de 1mA. Le courant de sortie sera alors cent fois plus grand c’est-à-dire qu’il sera de 100mA.

Supposons que nous pouvons prélever maintenant une certaine partie du signal de sortie et que nous le reportions à l’entrée de l’amplificateur. Ceci est possible en plaçant entre la sortie et l’entrée une résistance R_r comme indiqué en figure 2b. En choisissant convenablement la valeur de R_r, nous pouvons obtenir un courant i_r ramené à l’entrée qui est égal à une certaine fraction du courant de sortie i_u.

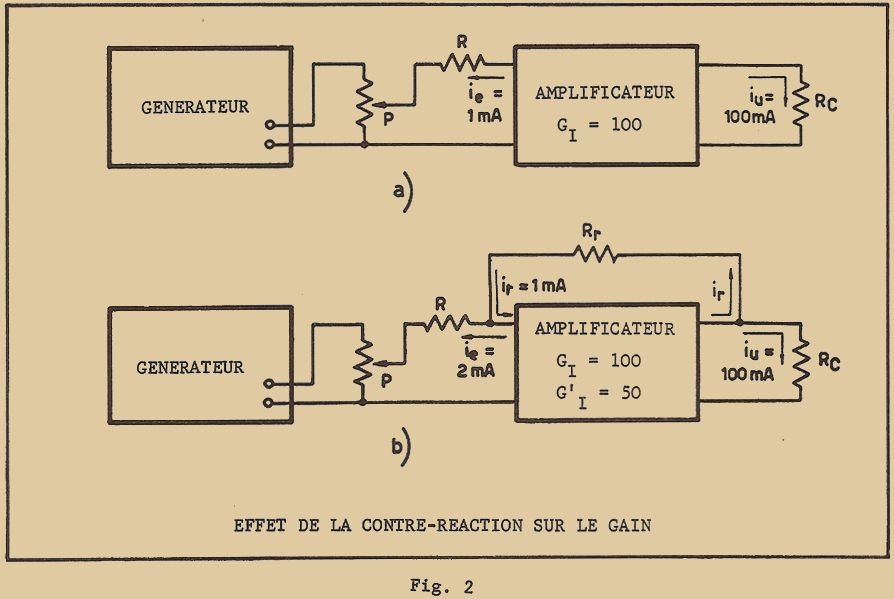
Si par exemple, nous faisons en sorte que i_r soit égal au centième de i_u, nous aurons i_r égal à 1mA. Nous dirons alors que le coefficient de réaction b est égal à 1/100, c’est-à-dire que b = 1/100. Nous avons donc :

i_r = b x i_u = 1/100 x 100 = 1mA

Supposons maintenant que le courant i_r, que nous appellerons courant de réaction, soit en opposition de phase avec le courant de commande ie délivré par le générateur.

De cette manière, le courant d’entrée de l’amplificateur, résultant de ie et de i_r, sera donné par la différence entre les deux courants ci-dessus et la réaction est appelée Réaction négative ou Contre-réaction.

Si nous voulons, comme dans le cas de la figure 2b, que le courant de sortie soit encore de 100mA, il faudra faire en sorte que le courant effectif de commande de l’amplificateur (c’est-à-dire la différence entre ie et i_r) soit encore de 1mA. Or comme i_r = 1mA il est absolument nécessaire que ie soit égal à 2mA. Le courant effectif de commande sera alors :

i_e – i_r = 2mA – 1mA = 1mA

Nous voyons maintenant, que le gain effectif en courant de l’amplificateur (défini comme étant le rapport i_u/i_e) est dans le cas de la figure 2b (avec contre-réaction) réduit par rapport au cas de la figure 2a (sans contre-réaction). Nous avons en effet maintenant :

G'_i = i_u/i_e = 100/2 = 50

au lieu de G_i = 100 comme auparavant.

Le gain G'_i avec contre-réaction est donc d’autant plus petit par rapport au gain G_i sans contre réaction que le coefficient de contre-réaction est plus grand.

On démontre que le gain G'_i est donné par la formule :

G'_i = G_i/D

où D, appelé Degré de contre-réaction, est donné à son tour par la formule :

D = 1 + (b x G_i)

Dans le cas de notre exemple, nous aurons :

D = 1 + (1/(100 ) x 100) = 1+ 1 = 2

Le degré de contre-réaction est donc égal à 2 et le gain G'_i est :

G'_i = G_i/D = 100/2 = 50

Le degré de contre-réaction exprime donc de combien de fois le gain d’un amplificateur contre-réactionné est plus petit que le gain qu’aurait l’amplificateur en l’absence de la contre-réaction.

Jusqu’à maintenant nous avons vu qu’en appliquant une contre-réaction à un amplificateur, le gain de celui-ci diminuait, et ce d’autant plus que le degré de contre-réaction était plus élevé. Nous n’avons pas encore vu quels en étaient le ou les avantages. Il semblerait en effet à première vue, que la contre-réaction soit un non-sens, puisqu’elle réduit le gain d’un amplificateur.

L’utilisation de la contre-réaction est cependant plus que justifiée en pratique par les énormes avantages qu’elle présente.

On démontre en effet, qu’en appliquant à un amplificateur un degré de contre-réaction D, les distorsions du signal de sortie sont réduites de D fois par rapport à celles qui existent en l’absence de la contre-réaction.

On démontre encore que la fréquence de coupure supérieure d’un amplificateur contre-réactionné est d’environ D fois plus élevée que celle du même amplificateur sans contre-réaction. De même, la fréquence de coupure inférieure est D fois plus petite. Ceci signifie donc qu’en appliqaunt une contre-réaction à un amplificateur, on améliore notablement sa courbe de réponse aux fréquences basses et élevées.

Soit un amplificateur qui délivre un signal de sortie avec 10% de distorsion et dont la courbe de réponse s’étend de 100Hz à 5kHz. Appliquons à cet amplificateur, un degré de contre-réaction égal à 2 ; la distorsion va être réduite à 5% ; les fréquences de coupure vont être maintenant aux environs de 50Hz et 10kHz respectivement.

D’autre part, l’utilisation de la contre-réaction présente encore un autre avantage qui est celui d’obtenir un amplificateur moins sensible aux variations des caractéristiques, comme par exemple dans le cas du remplacement d’un transistor par un autre du même type. Ceci permet une production en série plus homogène et uniforme, sans avoir à recourir à une sélection des transistors.

On applique en général la contre-réaction sur un ou deux étages d’un amplificateur au maximum.

Si on veut appliquer la contre-réaction à plus de deux étages, on peut le faire bien sûr, mais il faut prendre de grandes précautions pour éviter des accrochages qui peuvent se produire aux fréquences élevées ou au contraire pour des basses fréquences.

Ce n’est que dans un amplificateur à un seul étage que l’on peut appliquer un fort degré de contre-réaction sans risque d’accrochage. C’est pour cette raison que l’on préfère en général contre-réactionner séparément les étages d’un amplificateur, au lieu d’appliquer une seule contre-réaction à tout l’amplificateur.

Dans les récepteurs radio, on applique très souvent la contre-réaction aux étages de basse fréquence. Pour cela, on insère une résistance entre le secondaire du transformateur de sortie et la base du transistor driver (R₂₃ figure 1). Le degré de contre-réaction que l’on utilise en général est de l’ordre de quelques unités (5 à 10 au maximum) pour éviter une réduction trop importante du gain.

---

BATTERIES D'ALIMENTATION

Les circuits étudiés jusqu’à maintenant, et en général tous les appareils à transistors, peuvent être alimentés indifféremment soit par des batteries basse tension, soit par des redresseurs de courant alternatif ; mais l’utilisation des batteries est plus généralisée parce que les appareils à transistors d’emploi courant sont presque tous du type portable et les puissances absorbées pour leur alimentation sont faibles.

On peut toutefois faire remarquer que l’energie délivrée apr une batterie est beaucoup plus onéreuse que celle du réseau électrique. Ainsi par exemple, l’énergie d’une batterie de 4,5Volts que l’on utilise dans les montages expérimentaux "coûte" environ cinq cent fois celle du réseau électrique.

D’autre part, le coût est encore plus élevé pour les piles ordinaires des récepteurs portables du commerce. Il semblerait pour cette raison qu’il soit ridicule d’utiliser une batterie pour alimenter un appareil là où il y a une prise de courant alternatif et qu’il serait plus économique d’employer une alimentation redressée.

En réalité cependant, si l’on fait le calcul du taux d’amortissement d’une alimentation à redresseur, on trouve un délai d’environ trois ans, en utilisant le récepteur en moyenne deux heures par jour. Si on alimente par contre à l’aide d’une batterie un récepteur à sept transistors, on trouve une dépense de l’ordre de grandeur de celle qui est nécessaire pour alimenter en courant alternatif un récepteur classique à quatre tubes plus une valve : le prix d’une alimentation redressée ne se justifie donc pas.

C’est pour cette raison que l’emploi des piles et des batteries est largement diffusé dans les récepteurs transistorisés. C’est pour cela que je terminerai l’étude des circuits à transistors en passant en revue les principaux types de batterie.

Elles peuvent être subdivisées dans les groupes suivants :

• batteries électrochimiques primaires : représentées surtout par les piles sèches.
• batteries électrochimiques secondaires : représentées par les accumulateurs hermétiques au nickel-chrome.
• batteries spéciales : du type batteries solaires ou radio-actives. Chacune des batterie est constituée en général de plusieurs éléments identiques entr’eux.

Ces éléments sont reliés en série lorsque l’on a besoin d’une tension supérieure à celle formée par un seul élément. Ils peuvent être reliés aussi en parallèle si on a besoin de tension et de courant plus important.

Pour terminer l’étude des circuits, nous examinerons brièvement le principe de fonctionnement et la constitution des éléments des principales batteries utilisées dans les appareils à transistors selon la subdivision indiquée ci-dessus.

2 – 1 BATTERIES ÉLECTROCHIMIQUES PRIMAIRES (PILES AU CARBONE-ZINC ET AU MERCURE)

Les batteries de ce groupe se distinguent entr’elles selon la substance chimique qui les compose et suivant les réactions chimiques qui se produisent pendant leur fonctionnement, mais toutes dérivent de la pile Volta dont je vais rappeler le fonctionnement.

Si l’on immerge deux électrodes, une de zinc et l’autre de cuivre (ou de carbone), dans une solution acide (ou saline), on obtient entre ces électrodes une différence de potentiel capable d’alimenter en courant continu un circuit électrique extérieur. En d’autres termes, on peut dire que l’on a réalisé un dispositif qui fonctionne comme un "générateur de courant continu" et que ce dernier est parfaitement autonome en ce sens que l’énergie électrique est extraite des proprités chimiques des différents matériaux utilisés dans la réalisation de cette pile.

L’inconvénient principal de cette pile réside dans sa brève durée, car le courant ne se maintient pas constant, mais diminue graduellement jusqu’à s’annuler complètement et ceci très rapidement. On dit alors que la pile s’est polarisée.

Cette polarisation persite tant que l’on a pas éliminé l’hydrogène qui s’est formé sur l’électrode de cuivre (ou de carbone) pendant le fonctionnement. Cette polarisation a provoqué un accroissement considérable de la résistance inrerne de la pile et la diminution crrespondante du courant délivré.

Dans ce type de pile, pour éliminer l’hydrogène, on utilise des subtances chimiques dépolarisantes, c’est-à-dire qui sont avides du gaz qui se forme pendant le processus de polarisation. De cette façon, si on ne peut empêcher la production de l’hydrogène, on élimine cependant au fur et à mesure qu’il se forme dans la réaction chimique normale ; on assure ainsi à la pile une durée de vie beaucoup plus longue.

Les dépolarisants chimiques peuvent être liquides, solides, gazeux. Il est évident que dans les piles employées dans les appareils portables, on utilisera des dépolarisants solides ou gazeux. On peut aussi immobiliser, à l’aide de composés spéciaux, la solution acide ou saline (que l’on appelle électrolyte) interposée entre les deux électrodes, de façon à ce qu’il n’y ait pas de liquides libres susceptibles de se déplacer. On peut à ce moment utiliser la batterie sans précautions spéciales.

Les piles formées par des éléments à dépolarisant solide ou gazeux et par un électrolyte immobilisé, sont appelées dans le langage courant, des piles sèches.

La figure 3 représente un élément d’une pile sèche du type LECLANCHE, très uilisée dans les appareils portables.

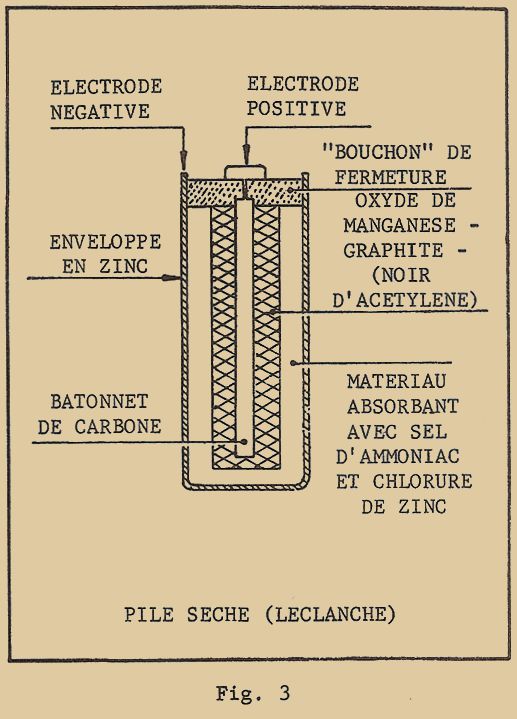
L’électrode positive est constituée par un bâtonnet de carbone tandis que l’électrode négative est constituée par l’enveloppe même qui est en zinc. Comme électrolyte, on utilise une solution d’ammoniac et de chlorure de zinc immobilisée par un matériau absorbant.

On entoure l’électrode positive (carbone), par une enveloppe qui contient un mélange d’oxyde de manganèse, de graphite en poudre et de noir d’acétylène. Ce mélange fonctionne comme dépolarisant.

En général, un tel type d’élément délivre une tension de 1,5V.

Pour obtenir des tensions plus élevées, il faut relier un certain nombre d’éléments en série. Pour avoir une tension de 3V, il faut réaliser une batterie de deux éléments en série, pour 4,5V, une batterie de 3 éléments, pour 6V , 4 … et ainsi de suite.

Semblables aux précédentes du point de vue de fonctionnement, sont les batteries à éléments superposés, appelés encore WAFER ou à Eléments Pastilles représentées en figure 4.

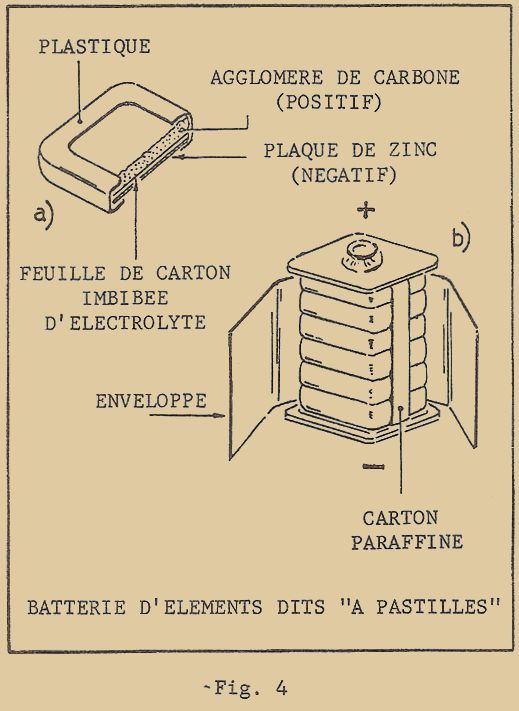
Chaque élément d’une telle batterie (figure 4a) est constitué par une plaque de zinc de forme carrée ou rectangulaire qui constitue l’électrode négative, un papier imprégné de l’électrolyte et appliqué sur la face supérieure du zinc, et un aggloméré de carbone et de dépolarisant qui constitue l’électrode positive.

La face inférieure du zinc est recouverte par une couche de vernis noir conducteur qui a pour rôle d’empêcher les réactions chimiques entre le zinc et les pastilles successives de la batterie.

Chaque pastille est recouverte sur les côtés par du plastique isolant qui sert à empêcher l’electrolyte de s’évaporer.

Un tel élément délivre une tension constante de 1,5V ; on superpose donc un certain nombre d’éléments comme indiqué en figure 4b, et en reliant en série les différents éléments, on peut obtenir toutes les tensions requises pour alimenter les appareils à transistors.

La figure 5 représente un autre type de batterie sèche qui est la pile au mercure ; cette pile est constituée essentiellement par du zinc, de l’oxyde de mercure et de l’hydrate de potassium (soude caustique).

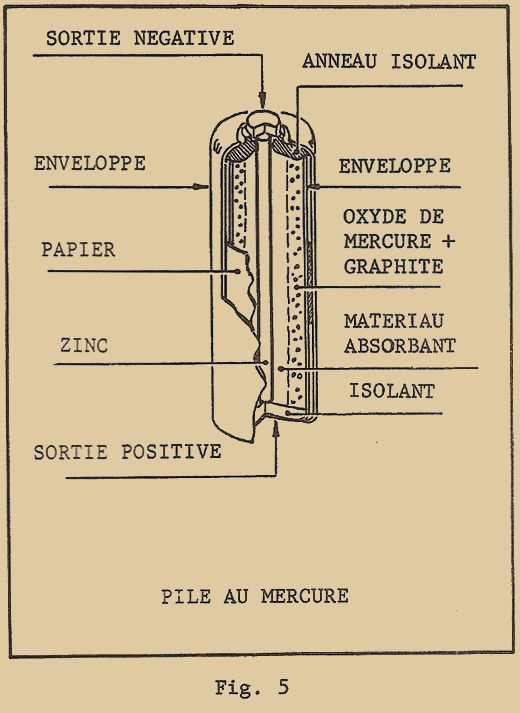
Les réactions chimiques ont lieu sur le zinc qui s’oxyde au contact de l’hydrate et sur l’oxyde de mercure qui est réduit en donnant du mercure métallique.

L’électrode de zinc (négatif) peut être préparée de différentes façons ; elle peut être constituée par des poudres fortement pressées en forme de cylindre creux (comme sur la figure 5), ou en disques ou sous forme de rubans de zinc très pur enroulés de façon à augmenter au maximum la surface de réaction.

L’oxyde de mercure dans le type de batterie de la figure 5, est disposé sur la couche la plus externe en contact avec l’enveloppe ; il est en général mélangés avec une fine poudre de graphite qui a pour rôle d’augmenter la conductibilité de l’électrode (positive).

L’electrolyte, l’hydrate de potassium, est immobilisé dans un matériau poreux et absorbant qui sépare l’électrode négative de l’électrode positive.

Le tout est enfermé dans une enveloppe en acier nickelé. La tension délivrée par les éléments au mercure est légérement inférieure à celle des éléments au carbone-zinc ; elle est de l’ordre de 1,3 V environ. On peut aussi réaliser avec ces éléments des batteries pour alimenter tous les appareils classiques à transistors.

2 – 2 BATTERIES ÉLECTROCHIMIQUES SECONDAIRES – (ACCUMULATEURS HERMÉTIQUES AU NICKEL CADMIUM)

Les batteries secondaires diffèrent des primaires en ce sens qu’après avoir cédé leur énergie électrique (décharge), elles peuvent à nouveau être rechargées si on les relie à un générateur approprié de courant continu.

Dans les batteries électrochimiques primaires, l’énergie électrique est obtenue à partir d’une énergie chimique par un processus irréversible : les opérations de transformation se font en sens unique.

Dans les batteries secondaires, des transformations analogues aux précédentes ont lieu, mais par contre il est possible de les inverser c’est-à-dire de reconstituer la substance chimique dans les mêmes proportions qu’au début de la décharge.

Il est à remarquer que les batteries de ce groupe, mieux connues sous le nom d’accumulateurs, sont beaucoup plus lourdes et plus encombrantes que les piles sèches. D’autre part, elles nécessitent des opérations de manutention, comme par exemple la vérification du niveau et l’addition périodique d’eau distillée ainsi que des précautions de manutention qui constituent un obstacle à leur utilisation dans les appareils du type portable.

La solution de ces problèmes ne pouvait être trouvée que dans la réalisation d’un accumulateur léger et absolument hermétique de façon à ce qu’il puisse être utilisé dans une position quelconque sans risque d’écoulement de l’électrolyte et sans obligation de retoucher périodiquement le niveau de ce dernier.

L’herméticité des accumulateurs classiques est pratiquement impossible à cause de l’apparition des gaz (oxygène et hydrogène) surtout vers la fin de la charge. Il faut donc chercher à supprimer la formation des gaz ou bien d’obtenir leur recombinaison de façon qu’il ne soit plus nécessaire de laisser ouvert les bacs.

La solution du problème a été trouvée par un nouveau procédé qui supprime complètement la libération de l’hydrgène et qui réalise la recombinaison de l’oxygène libéré avec les masses actives des électrodes ; par ce système, on évite la formation d’une pression excessive à l’intérieur de l’accumulateur et on peut fermer hermétiquement l’enveloppe.

Les électrodes sont du type nickel-cadmium, déjà employés dans d’autres types d’accumulateurs. La masse active de l’électrode positive est constituée par de l’hydroxyde de nickel, tandis que celle de l’électrode négative est formée par du cadmium et du fer finement broyés et mélangés. L’electrolyte est contituée par une solution de potasse caustique très pure.

La figure 6 illustre trois types d’accumulateurs hermétiques. Le type de la figure 6a se présente sous la forme d’une capsule métallique et qui par simple superposition permet de réaliser des batteries de tension quelconque ; ces éléments, de capacité relativement faible, peuvent remplacer les piles sèches à éléments plats utilisés surtout dans de petits appareils de prothèse auditive.

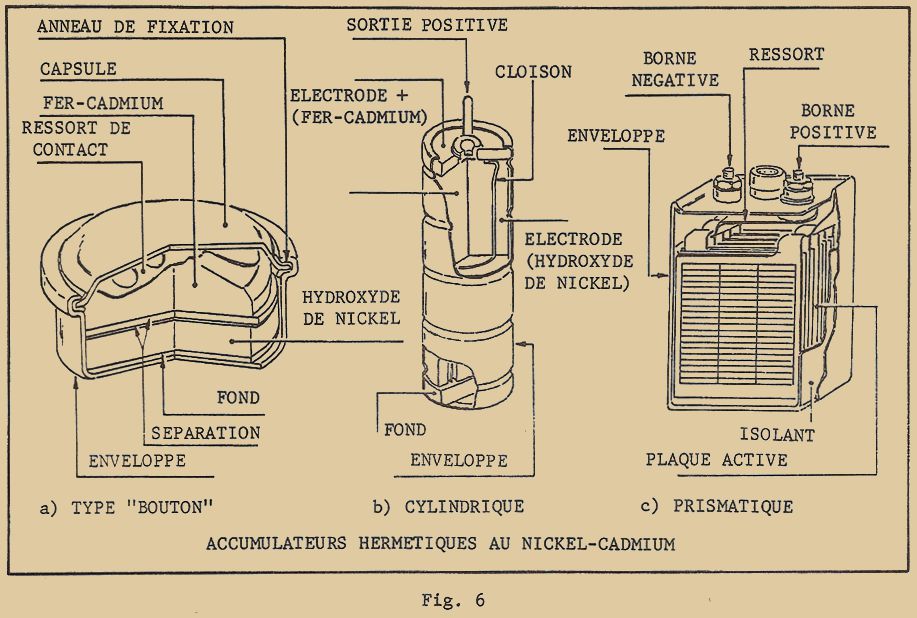
Le type de la figure 6b se présente sous la forme cylindrique et est contitué par des éléments de capacité un peu plus grande que celle du type précédent ; ce type peut remplacer les piles cylindriques classiques utilisées dans les récepteurs radio.

Le type de la figure 6c en forme de prisme à section carrée ou rectangulaire possède une capacité encore plus grande que celle des types précédents ; il peut donc servir à alimenter des appareils portables qui absorbent déjà une certaine puissance, beaucoup plus importante que celle qui est consommée dans les récepteurs à transistors classiques.

On peut voir en figure 6, par des coupes appropriées, les détails de construction des différents types ; le principe de fonctionnement ne diffère pas d’un type à l’autre. Tous délivrent en régime de décharge, une tension de 1,22V, et sont rechargés sous une tension comprise entre 1,35 à 1,50V.

2 – 3 BATTERIES SPÉCIALES – (PILES SOLAIRES ET RADIO-ACTIVES)

Pour conclure cette brève étude sur les batteries, nous allons examiner la constitution des piles solaires et des piles radio-actives (figure 7), qui actuellement ont trouvé des applications dans les appareillages transistorisés des missiles, des satellites artificiels et des navires cosmiques.

Le principe de fonctionnement de ces deux types de batterie est semblable ; on les appelle d’ailleurs quelquefois des "Radio-batteries".

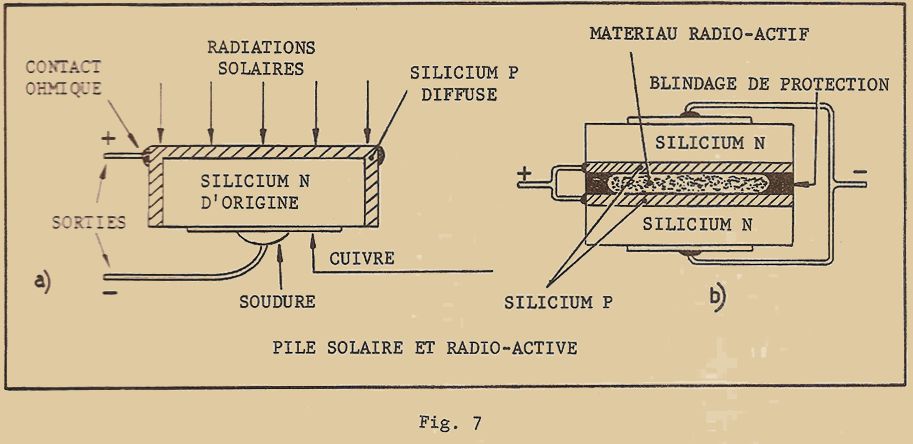
Une radio-batterie est constituée essentiellement d’une jonction P-N de silicium ou d’un autre semi-conducteur, ou bien d’un système de jonctions P-N reliées en série entr’elles, ou en parallèle, ou en série-parallèle.

Si la jonction P-N est exposée à la lumière, ou en général à des radiations (comme par exemple celles qui sont émises par une substance radio-active), il apparait à ses bornes une différence de potentiel qui peut être utilisée comme force électromotrice.

En se basant sur ce principe, il a été possible de trouver la solution à un problème posé depuis tous les temps, c’est-à-dire d’utiliser en partie l’énorme réserve d’énergie constituée par la lumière solaire (il suffit en effet de penser que l’énergie solaire rayonnée sur la terre a une puissance moyenne de quelques 1000 W par mètre carré).

Il a été d’autre part possible de réaliser sur le même principe des piles de durée très grande, en utilisant des matériaux radio-actifs produits artificiellement par des procédés de physique atomique.

On a réalisé récemment aux Etats-Unis une petite batterie radio-active dont la durée, calculée théoriquement, devrait être de l’ordre de trente ans.

On peut prévoir facilement qu’avec les progrès techniques actuels, on pourra réaliser bientôt des batteries solaires et radio-actives utilisables dans les appareils d’usage courant. Pour le moment cependant, de telles batteries sont encore trop coûteuses et ne peuvent être utilisées couramment.

---

EXERCICES DE RÉVISION SUR LA 28^ème LEÇON THÉORIQUE

1 – Que provoque la contre-réaction sur le gain de l’amplificateur ?

2 – Comment appelle-t-on encore la contre-réaction ?

3 – Quels sont les avantages de la contre-réaction ?

4 – Qu’indique le degré de contre-réaction ?

5 – Si le gain d’un amplificateur en l’absence de contre réaction est de 1000 et si le degré de contre-réaction est 10, quelle est la valeur du coefficient de réaction ?

6 – Un amplificateur en l’absence de contre-réaction, a un gain de 80, une bande passante s’étendant de 50Hz à 10.000Hz et une distorsion de 5%. On lui applique un degré de contre-réaction de 5. Quelles sont les nouvelles valeurs du gain, de la distorsion et de la bande passante ?

7 – Quels sont les éléments essentiels d’une pile sèche ?

8 – Par quoi les accumulateurs se distinguent-ils des batteries dites primaires ?

9 – Comment est constituée une batterie solaire ?

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 27^ème LEÇON THÉORIQUE

1 – L’amplificateur à fréquence intermédiaire (FI) est du type sélectif et accordé sur la fréquence de la FI (par exemple 480kHz).

2 – Le détecteur délivre un signal constitué d’une composante continue proportionnelle à l’intensité du signal reçu et d’une composante alternative dont l’allure suit celle de l’enveloppe de modulation ; cette dernière composante constitue le véritable signal BF utile.

3 – La constante de temps d’un circuit RC est donnée par le produit de la valeur de R, par la valeur de C.

4 – La constante de temps exprime le temps qui s’écoule pour que la tension aux bornes de C se réduise de 2,72 fois, quand C se décharge dans R

5 – R = 1 MΩ = 106 Ω

C = 250 pF = 250.10-12

d’où RC = 106 x 250.10-12 = 250.10-6 seconde = 250µS.

6 – Le RAS sert à régler de façon automatique la sensibilité du récepteur en fonction de l’intensité du signal reçu.

7 – En l’absence de modulation le condensateur C du circuit de détection se charge à la valeur crête de la porteuse FI.

8 – Dans un récepteur à transistors, la tension RAS doit être positive par rapport à la masse de façon à réduire le gain du transistor HF en présence d’un signal intense.

9 – Au bout d’un temps égal à la constante de temps, la tension aux bornes du condensateur s’est réduite à 36,7% de sa valeur primitive de départ.

Fin de la leçon 28

---

LECON 29

CIRCUITS D’ALIMENTATION

Après l’étude des circuits à transistors, il convient d’examiner aussi les circuits que l’on peut réaliser avec des diodes cristal en vue de certaines applications en technique radio.

Je vous ai dit dans la sixième leçon théorique que la diode cristal pouvait être utilisée en Redresseur en la faisant travailler dans sa caractéristique directe et dans la partie horizontale de sa caractéristique inverse ; elle pouvait aussi être utilisée en Stabilisatrice de tension si on la faisait travailler dans la partie verticale de sa caractéristique inverse, c’est-à-dire à la tension Zener. Elle pouvait aussi être considérée comme un condensateur variable, si elle travaillait dans la région horizontale de sa caractéristique inverse.

Mais ce ne sont pas les seules applications possibles. On peut encore utiliser la diode comme une Résistance variable en la faisant travailler dans la région coudée de la caractéristique directe où la résistance varie avec le point de fonctionnement. Si on exploite sa propriété appelée "Effet Tunnel", on peut l’utiliser comme mélangeuse, oscillatrice ou comme élément de commutation dans les circuits à deux positions stables. Elle peut enfin être utilisée comme une diode photorésistante dans un circuit de commande si on exploite sa sensibilité à la lumière.

Entre toutes ces applications possibles, les deux plus importantes en pratique radio-électrique sont les deux premières, c’est-à-dire comme redresseuse et stabilisatrice.

Les redresseurs à cristal de silicium ou de germanium sont devenus de nos jours d’un emploi courant, étant donnés leur sécurité dans le fonctionnement, leur rendement élevé et leur encombrement réduit.

Toutefois ils présentent des limitations et en particulier ils sont très sensibles aux surcharges ; il convient donc d’examiner soigneusement leur fonctionnement, afin de savoir comment les utiliser avec toute la sécurité nécessaire.

Les diodes Zener sont devenues d’un emploi courant comme stabilisateur de tension et comme éléments aptes à délivrer des tensions de référence dans les alimentations stabilisées. Nous étudierons donc un régulateur de tension simple, dans lequel nous mettrons bien en évidence les caractéristiques électriques générales de la diode Zener et les limitations qui lui sont propres.

Avant de commencer l’étude des circuits redresseurs les plus simples il faut se rappeler que la tension alternative du secteur a une fréquence de 50 Hz, correspondant à une période de 20 mS (son allure sinusoïdale a été représentée en figure 1 de la théorique 15).

En général, cette tension est exprimée par sa valeur efficace ; la valeur de crête (ou valeur maximum ou valeur de "pic") et la valeur de crête-crête sont données par les formules suivantes :

v_p = 1,41 V_eff   et v_pp = 2 vp

Si la tension du secteur est de 220 V (efficace), on aura :

v_p = 1,41 x 220 = 310 V (environ)

v_pp = 2 x 310 = 620 V (environ)

Si la tension alternative est 4,5 V (en utilisant par exemple un transformateur abaisseur) on aura :

v_p = 1,41 x 4,5 = 6,3 V (environ)

v_pp = 2 x 6,3 = 12,6 V (environ)

La valeur de crête d’une tension alternative que l’on peut redresser peut servir, par exemple, à déterminer la valeur maximum du courant direct de la diode dans ses conditions de fonctionnement normales, tandis que la valeur de crête-crête servira à déterminer la tension inverse maximum qui sera appliquée aux bornes de cette même diode.

Rappelons brièvement les définitions relatives aux tensions et aux courants dans une diode.

La tension qui apparait pendant le fonctionnement sur l’anode (figure 1, Théorique 6) peut être positive ou négative par rapport à la cathode. Quand la tension est positive, on dit que la polarisation est directe et que la diode travaille dans la région de sa caractéristique directe (figure 3, Théorique 6) : elle présente dans ce cas, une résistance minimum au passage du courant. Quand au contraire la tension de l’anode est négative par rapport à la cathode on dit que la diode est polarisée en inverse : elle travaille alors dans la région de sa caractéristique inverse et offre au passage du courant, une résistance maximum.

Pour se souvenir facilement de ces définitions, il suffit de remarquer que la tension directe est celle qui est positive et que la tension inverse est celle qui est négative, en prenant toujours comme référence le potentiel de la cathode.

Comme pour les tensions, on distingue le courant direct et le courant inverse ; le premier va de l’anode vers la cathode lorsqu’une tension directe est appliquée ; le second va en sens opposé du premier (cathode-anode) lorsqu’une tension inverse est appliquée.

Nous allons passer maintenant à l’étude des circuits.

1 - REDRESSEUR A UNE ALTERNANCE

Le circuit redresseur le plus simple que l’on puisse imaginer est constitué par une diode en série avec un condensateur ou une résistance (figure 1).

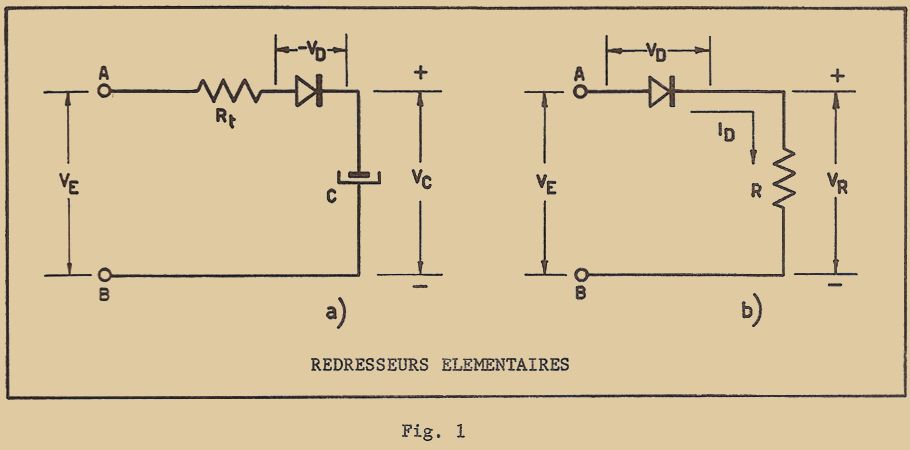
En pratique, il n’existe pas de charges purement résistives ou capacitives ; mais il convient d’examiner séparément ces deux cas, car ainsi nous pourrons bien mettre en évidence les limites de tension et de courant entre lesquelles la diode devra fonctionner.

1 – 1 REDRESSEUR A CHARGE CAPACITIVE

On considère le schéma de la figure 1a, où sont représentés une diode et un condensateur reliés en série par rapport au générateur délivrant la tension alternative V_E.

Entre ces éléments on a placé une résistance Rt qui a pour rôle de limiter le courant de charge du condensateur au moment de la fermeture de l’interrupteur (ce courant au départ est très intense et peut détruire la structure de la diode).

Lorsque l’alternance positive de la tension V_E arrive au point A, la diode se rouve polarisée dans le sens direct et le courant direct qui en résulte charge le condensateur à la tension continue V_C. Cette tension s’accroît lorsqu’arrivent les alternances positives successives (étant donné que la charge du condensateur augmente) et au bout d’un certain temps elle atteint une valeur égale à la valeur crête de la tension d’entrée. Ainsi, si la tension d’entrée est de 220 V (volts efficaces), V_C atteindra 220 V x 1,41 = 310 V (continus) environ. Cette dernière valeur correspond, comme nous l’avons vu tout à l’heure à la valeur de crête de la tension alternative.

Supposons que la tension à la sortie V_C a atteint sa valeur de régime, c’est-à-dire qu’elle est continue et constante comme le montre le graphique de la figure 2.

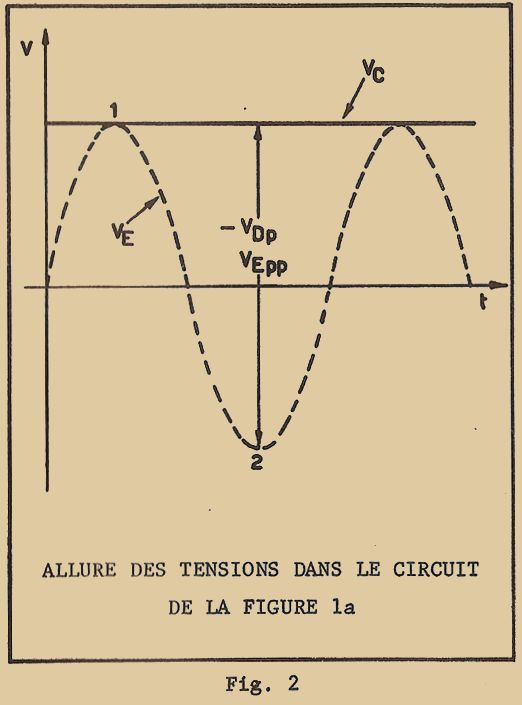
Dans ces conditions, lorsque V_E après avoir atteint la valeur de crête positive (point 1), commence à diminuer, la tension V_Dp appliquée à la diode (figure 1a) commence à croître parce que du côté de la cathode, le condensateur maintient le potentiel (qui est positif) tandis que sur l’anode le potentiel décroît : la tension appliquée à la diode se trouve être négative ; c’est donc une tension inverse (-V_Dp).

La tension inverse -V_Dp continue à croître pendant l’alternance négative et atteint sa valeur maximum (-V_Dpp) lorsque la tension d’entrée prend sa valeur de crête négative (point 2).

Sur le graphique de la figure 2, on peut voir immédiatement que –V_Dpp est égal à la valeur de crête à crête (V_Epp) de la tension d’entrée V_E. Ainsi, lorsque l’on connait la valeur efficace (ou la valeur de crête) de V_E, on peut calculer facilement la valeur maximum de la tension inverse qui sera appliquée à la diode.

La tension inverse maximum qu’une diode peut supporter est toujours indiquée dans les données techniques des constructeurs.

Celle-ci correspond à un point de la caractéristique inverse qui est choisi avec une certaine marge de sécurité par rapport à la région où se produit le phénomène de ZENER (théorique 6) et où il y aurait un accroissement rapide du courant inverse et une destruction interne de la diode.

Lorsque l’on connait la valeur maximum admissible – V_DpM, on peut calculer facilement la valeur efficace de la tension maximum d’entrée V_EM par la formule :

V_EM (valeur efficace) = -V_DM/2,82

Ainsi pour la diode au silicium OA 211, la valeur maximum admississible est de 800 V et pour la diode au germanium OA 95 elle n’est que de 115 V. En appliquant la formule précédente, nous obtenons :

V_EM  = 800/2,82 = 283 (volts efficaces) pour la diode au silicium

V_EM  = 115/2,82 = 41 (volts efficaces) pour la diode au germanium

Si nous utilisons une diode OA 211, nous pourrons appliquer à l’entrée du redresseur sous charge capacitive, une tension secteur quelconque inférieure à 283 V , avec une diode OA 95, la tension d’entrée ne devra en aucun cas dépasser 41 V.

Il est intéressant de remarquer, que dans le circuit de la figure 1a, la diode se trouve toujours polarisée en inverse à partir de l’instant où la charge du condensateur est terminée ; à ce moment, le circuit n’est parcouru que par un très faible courant inverse, pratiquement négligeable. Ceci est dû au fait que le condensateur conserve sa charge et que la tension de sortie V_C se maintient à une valeur que l’on peut considérer comme étant la valeur de crête de la tension positive d’entrée.

1 – 2 REDRESSEUR CHARGÉ PAR UNE RÉSISTANCE PURE

Nous considérons maintenant le schéma de la figure 1b, où la charge est constituée par la résistance R.

Dans le projet d’utilisation de la diode sous charge capacitive, le problème le plus important était la tension maximum inverse, -V_DpM ; maintenant que la charge est une résistance pure, le problème est de connaître le courant maximum direct que peut supporter la diode en fonctionnement. En effet, tandis que dans le premier circuit on avait passage du courant direct seulement pendant la charge du condensateur, dans le second, on a passage du courant direct (I_d) chaque fois qu’arrive sur l’anode une alternance positive de la tension d’entrée V_E. En effet, tandis que la tension de sortie V_C se maintient continue et variable (en ce sens qu’elle suit exactement l’allure du courant I_d) dans le cas de la figure 1b.

Quand sur la borne A (figure 1b) arrive l’alternance positive de V_E, la diode se trouve polarisée en sens direct ; le courant qui traverse le circuit est le courant direct I_d. Ce courant parcourt la résistance R et détemine une chute de tension VR aux bornes de celle-ci.

Quand par contre sur la borne A arrive l’alternance négative, la diode se trouve en polarisation inverse ; toute la tension d’entrée s’établit aux bornes de la diode en provoqaunt un courant inverse très faible ; donc la chute de tension aux bornes de R est négligeable devant la tension de sortie VR.

Pour étudier le fonctionnement de ce circuit, il faut encore tenir compte de ce que l’intensité du courant direct dépend des valeurs de la tension d’entrée et de la résistance totale du circuit. Cette résistance totale est donnée par la résistance de charge et par la résistance dynamique de la diode.

Nous allons recourir, dans l’étude qui va suivre, à la méthode graphique (figure 3) qui permet de réunir en une seule représentation les lois qui régissent les grandeurs caractéristiques du circuit lorsque celui-ci fonctionne en polarisation directe de la diode. Nous étudierons après les conditions en polarisation inverse.

Le circuit de la figure 1b est représenté complètement dans le graphique de la figure 3, par les données suivantes :

• Caractéristique directe (qui est celle d’une diode au germanium, à la température ambiante de 25 °C).
• Tension d’entrée (V_eff  = 4,5 V ; V_Ep = 6,3 V).
• Résistance de charge (représentée par les droites qui passent par les points de fonctionnement L, L’, L’’ et L_o ; R = 210Ω

La caractéristique directe a été dessinée selon les données du constructeur.

La tension d’entrée est représentée par l’alternance positive d’un signal sinusoïdal par rapport à l’axe des temps t (axe vertical) et à l’axe horizontal V_Dp (commun, lui, avec l’axe V_Dp de la caractéristique). Les droites de charge sont toutes parallèles puisqu’elles représentent la même résistance (R = 210Ω) et que par conséquent elles ont toutes la même pente.

Pour vérifier que ces droites de charge représentent effectivement la résistance de 210Ω, il suffit de prolonger l’une d’elle, par exemple celle qui passe par le point de fonctionnement L jusqu’à ce qu’elle coupe laxe I_d au point D ; on peut lire ainsi la valeur de la tension au point A sur l’axe V_Dp et la valeur du courant au point D sur l’axe I_d.

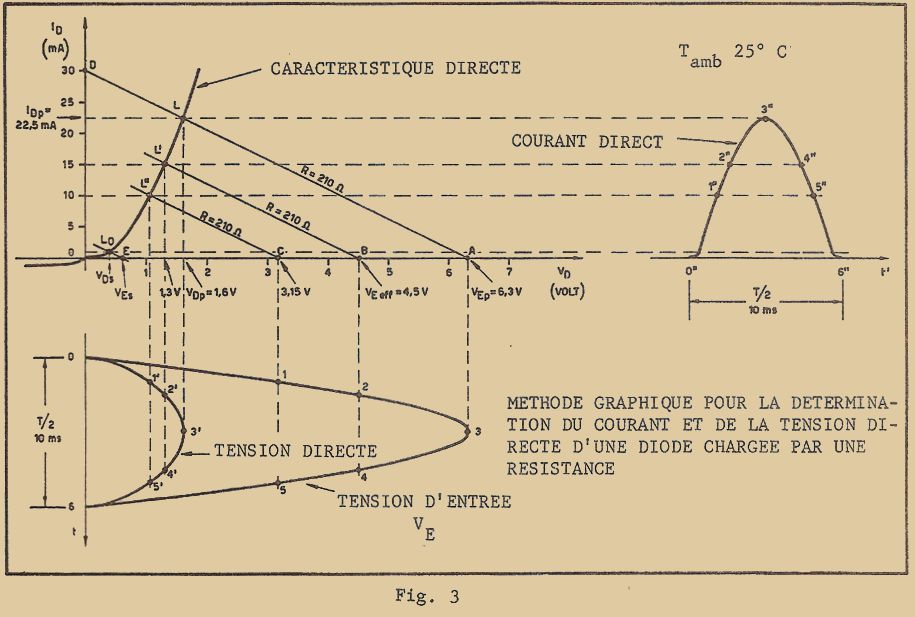
Dans le cas de l’exemple, la tension est égale à la valeur de crête, (V_Ep = 6,3 V) de la tension d’entrée et le courant est de 30mA environ.

Cette opération équivaut à supposer que la diode est en court-circuit et que toute la tension d’entrée (valeur de crête) est appliquée à la résistance R = 210Ω ; le courant qui est ainsi déterminé est celui qui passerait dans la résistance de charge si on appliquait à cette dernière, une tension de 6,3 V.

Connaissant les valeurs de la tension (6,3 V) et du courant (30mA = 0,03 A) on peut vérifier que la valeur de R est bien donnée par la formule de la loi d’ohm :

R = V/I = 6,3/0,03 = 210Ω

Vous pouvez vérifier facilement que la valeur correspondant aux autres droites de charge parallèles reste la même : en effet, toutes les droites parallèles à la droite AD déterminent des segments proportionnels sur les axes ce qui fait que le rapport tension/courant (V/I) reste le même (R = 210Ω).

On peut maintenant déterminer facilement sur la caractéristique directe les points de fonctionnement de la diode pour chaque valeur de la tension d’entrée V_E.

Entre les différentes valeurs de V_E, quelques-unes sont particulièrement importantes, comme celles par exemple qui correspondent aux points 0 et 6 (zéro volt), 1 et 5 (3,15 V), 2 et 4 (4,5 V = V_Eeff), 3 (6,3 V = V_Ep). Ces points sont ceux de l’alternance positive du signal d’entrée.

Aux points 0 et 6 correspond le point de fonctionnement 0 de la caractéristique ; pour ces points, la tension et le courant direct sont égaux à zéro.

Aux points 1 et 5 correspond le point de fonctionnement L’’, pour lequel la tension directe V_Dp est égale à 1 V environ et le courant direct I_d à 10mA environ.

Aux points 2 et 4 correspond le point de fonctionnement L’ pour lequel la tension directe V_Dp est égale à 1,3 V environ et I_d à 15mA.

Enfin au point 3 correspond le point de fonctionnement L qui est le maximum en ce sens qu’il correspond à la tension de crête de la tension d’entrée. Pour ce point, on obtient la valeur maximum de la tension directe (V_Dpp = 1,6 V) et la valeur maximum du courant direct (I_Dp = 22,5mA).

Nous pouvons représenter la tension directe sur le même graphique que celui représentant la tension d’entrée ; les points correspondant sont repérés 0, 1’, 2’, 4’, 5’ et 6. Cette courbe donne l’allure de la tension directe aux bornes de la diode.

Nous pouvons aussi représenter le courant direct I_d en reportant les points 0’’, 1’’, 2’’, 3’’, 4’’, 5’’ et 6’’. Cette courbe donne l’allure du courant direct dans la diode.

Outre les points de fonctionnement L’’, L’ et L, il convient de considérer encore le point de fonctionnement L_o qui se trouve dans la région de courbure de la caractéristique.

En correspondance avec le point L_o, on lit la tension directe de la diode V_Dps, dite tension de Seuil qui est une donnée caractéristique de chaque type de diode, car elle indique la limite inférieure de la tension V_Dp où le rendement du redresseur est pratiquement égal à zéro. Connaissant V_Dps (pour les diodes au germanium, elle est au maximum égale à 0,5 V, tandis que pour les diodes au silicium elle est de l’ordre de 0,8 V), on peut déterminer L_o ; ensuite, à l’aide de la droite de charge qui passe par L_o, on trouve la valeur de V_Es qui correspond au point d’intersection de cette droite de charge avec l’axe V_Dp. La valeur de V_Es indique la valeur de la tension d’entrée qui détermine aux bornes de la diode une tension directe égale à la valeur du seuil.

La détermination de V_Es est très importante dans le cas où l’on veut redresser une tension très basse (de quelques volts) comme dans l’exemple vu ci-dessus ; en effet, plus la tension appliquée à la diode est faible, plus son rendement sera bas (le rendement est le rapport entre la tension de sortie et la tension d’entrée du circuit).

En général, pour que le rendement du redresseur soit élevé, il faut que la valeur de crête de la tension sinusoïdale d’entrée soit à peu près dix fois la valeur de V_Es. Dans le cas de l’exemple, V_Es est de l’ordre de 0,6 V (environ) et la valeur de crête de la tension d’entrée est supérieure à 6 V (V_Ep = 6,3 V).

Encore plus importante que la tension de seuil, est la valeur maximum du courant direct admissible (I_DM), pour une marge de sécurité suffisante pour la diode.

Les renseignements techniques sur la diode OA 95 donnent un courant I_DM = 150mA, valeur déterminée pour une tension V_E sinusoïdale ; ainsi, dans le cas de notre exemple, où le courant maximum est I_Dp = 22,5mA, la marge de sécurité est très grande.

Nous avons étudié jusquà maintenant le fonctionnement du circuit de la figure 1b pendant la polarisation directe de la diode ; pour conclure cette étude, encore faut-il voir ce qui se passe lorsque ce même circuit se trouve en polarisation inverse, c’est-à-dire lorsque sur son anode arrive l’alternance négative de la tension d’entrée.

Quand la diode est polarisée en inverse, la chute de tension aux bornes de R est pratiquement négligeable, car le courant inverse qui traverse la résistance est lui-même extrêmement faible ; ainsi presque toute la tension d’entrée se touve aux bornes de la diode et correspond à la tension inverse. Dans ces conditions, nous pourrons retenir que la tension inverse maximum est égale à la valeur de crête de V_E (V_Ep = 6,3 V) comme il en résulte sur le graphique de la figure 4.

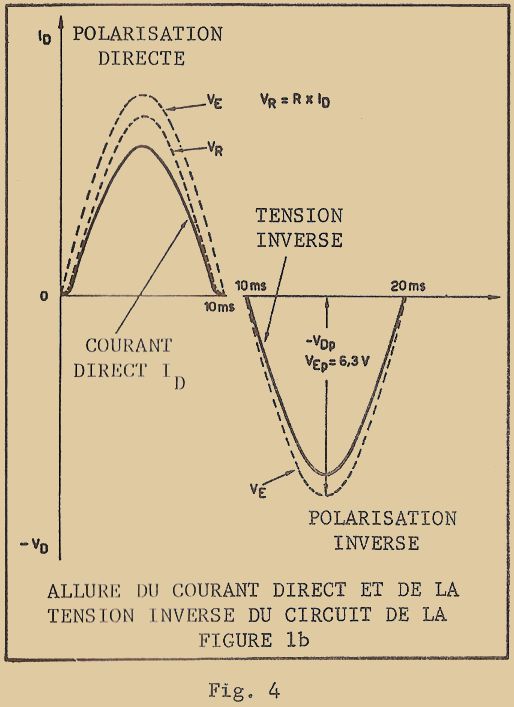
En nous rappelant ce qui advenait pour un circuit chargé par une capacité pure, nous voyons immédiatement que dans ce dernier cas, la tension inverse maximum est plus faible (en effet dans le circuit à charge capacitive, - V_Dpp était égale à la valeur de crête à crête de V_E (figure 2). Nous en déduirons que dans le circuit actuel, nous pourrons appliquer une tension d’entrée maximum double de celle que l’on pouvait admettre lorsque la charge était purement capacitive. Nous pourrons ainsi appliquer une tension de 82 volts efficaces au lieu des 41 V calculés précédemment pour la diode OA 95 et 566 volts efficaces au lieu de 283 V pour la diode au silicium OA 211.

Si nous voulions ainsi augmenter la tension d’entrée de 4,5 V à 82 volts (pour la diode OA 95), nous devrions aussi augmenter la valeur de la résistance de charge jusqu’à 546Ω afin d’éviter que le courant direct (I_d) ne dépasse la valeur maximum admissible.

Je vous ai représenté aussi dans le graphique de la figure 4 l’allure de la tension de sortie VR ; il suffit de remarquer que son allure est la même que celle du courant I_d, puisqu’elle est constituée par la chute de tension dûe au passage de I_d dans la résistance R (VR = R x I_d). Ainsi, sa valeur est proportionnelle à tout moment à l’intensité du courant et les deux formes d’ondes sont donc parfaitement identiques.

1 – 3 REDRESSEUR CHARGÉ PAR RÉSISTANCE ET CAPACITÉ

Le circuit de la figure 1a peut être modifié comme indiqué à la figure 5a où une résistance R a été placée en parallèle sur le condensateur C. Le transformateur qui délivre la tension d’entrée V_E a été représenté aussi.

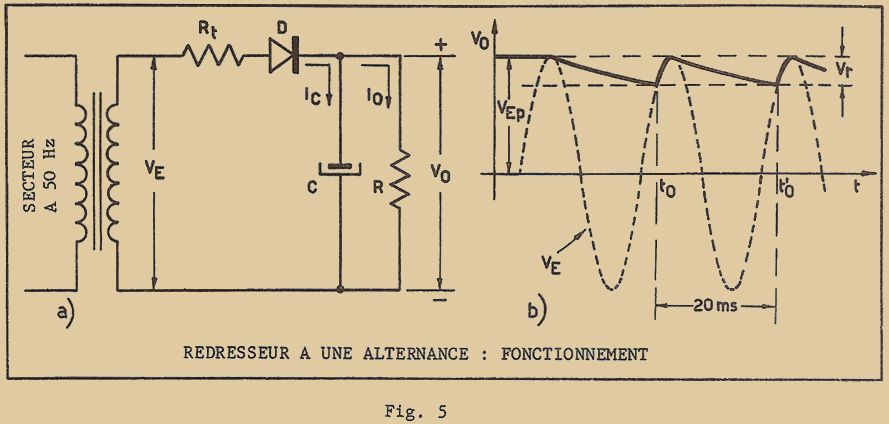
La résistance R peut-être remplacée par l’appareil que l’on désire alimenter par le courant redressé (I_o).

Si R est infiniment grand, le courant I_o est pratiquement négligeable : on retrouve alors les conditions de fonctionnement décrites dans le circuit à charge purement capacitive. Dans ce cas, la tension de sortie Vo est continue et constamment égale à la valeur de crête de la tension d’entrée V_E. Ces conditions peuvent être vérifiées chaque fois que la charge n’absorbe pas de courant et que le redresseur fonctionne à vide. Dans ce cas, il faut tenir compte dans le projet de la tension inverse maximum (-V_DpM) admissible par la diode.

Lorsque la charge absorbe un certain courant, la tension à la sortie ne reste plus parfaitement constante, mais présente une ondulation V_r (figure 5b) appelée Tension de ronflement ; d’autre part, la valeur de Vo est inférieure à la valeur de crête de la tension à l’entrée à cause de la chute de tension aux bornes de la diode et de la résistance Rt qui représente la résistance du transformateur.

On peut dire que ces nouvelles conditions de fonctionnement sont intermédiaires entre celles des circuits chargés par une capacité seule ou par une résistance seule. Toutes les limitations que nous avons vues au sujet des circuits de la figure 1 restent évidemment valables.

Pour expliquer l’allure particulière de la tension de sortie Vo et surtout la présence de la tension de ronflement V_r, il faut considérer le fonctionnement du condensateur après l’adjonction de la résistance R dont la valeur est notablement plus faible que celle de la résistance inverse de la diode.

Nous allons suppposer qu’au départ la tension de sortie Vo est continue et égale à la valeur de crête V_Ep de la tension d’entrée, c’est-à-dire que le redresseur fonctionne à vide.

Lorsque l’on branche la résistance R, le condensateur commence à se décharger dans R et la tension diminue à une vitesse qui est fonction de la valeur de la constante R x C (où la résistance est exprimée en ohms et la capacité en farads) jusqu’à ce qu’elle devienne égale à nouveau à la valeur de la tension alternative V_E. On suppose que cette égalisation a lieu à l’instant to. Comme les tensions d’entrée et de sortie sont égales, la tension appliquée aux bornes de la diode est nulle et le courant I_d est nul lui aussi. Mais à partir de to, la tension V_E augmente en suivant une allure sinusoïdale ; la diode se trouve alors polarisée dans le sens direct et un courant I_d traverse le circuit. Le courant se partage en IC qui recharge le condensateur et I_o qui alimente la charge résistive et fait ainsi croître la tension de sortie Vo. Quand, après avoir atteint la valeur de crête, la tension V_E va commencer à décroître, le courant I_d va diminuer aussi, et va finir par s’annuler en même temps que va s’annuler la différence existant entre les tensions d’entrée et de sortie.

A partir de cet instant et pendant toute la durée du cycle, la diode va se trouver polarisée en inverse et il n’y aura plus passage de courant de l’entrée vers la sortie (I_d = 0).

Cependant le courant I_o qui alimente la charge résistante ne va pas s’annuler et la tension Vo non plus, car intervient alors la décharge du condensateur. Celui-ci en effet ne peut se décharger dans la résistance inverse de la diode (qui est très élevée) ; il ne peut donc se décharger que dans la résistance de charge R.

La tension à la sortie continue à diminuer et atteint une valeur d’autant plus basse que la constante de temps (égale au produit R x C) est plus faible. A un certain moment arrive une nouvelle alternance positive de V_E ; la tension inverse de la diode s’annule et commence un nouvel intervalle de temps où il y a à nouveau passage du courant direct. La tension à la sortie recommence à augmenter suivant l’allure déjà vue.

Si l’on observe le graphique de la figure 5b, on remarque que pour chaque cycle de la tension d’entrée V_E, c’est-à-dire pendant les 20 mS qui séparent to et t’o, on a un cycle complet de la tension de ronflement V_r ; on en déduit que V_E et V_r ont même fréquence (f = 50 Hz).

Si l’on veut obtenir à la sortie une tension à faible ondulation (comme celle qui est nécessaire pour alimenter un amplificateur basse fréquence ou un récepteur radio), il faut que la constante de temps de la charge (R x C) soit inférieure ou au plus égale au rapport 10/f, où f est la fréquence de la tension alternative V_E.

Pour un réseau à 50 Hz, la valeur de la constante de temps nécessaire doit être de :

10/50 = 0,2 s (= 200.000 µS).

Si la résistance de charge est de 500Ω, la capacité du condensateur doit-être :

C = 0,2/R = 0,2/500 = 0,0004 F (= 400 µF).

En connaissant C, R et la fréquence de V_E (qui en général est 50 Hz), on peut déterminer le pourcentage de la valeur efficace de la tension de ronflement V_r par rapport à la valeur moyenne Vo (figure 5b) de la tension de sortie, en prenant la formule suivante :

X = 6,28 x f x C x R

où f est en hertz, C en farad, R en ohm.

et en utilisant le graphique pour redressement à une alternance représenté en figure 6.

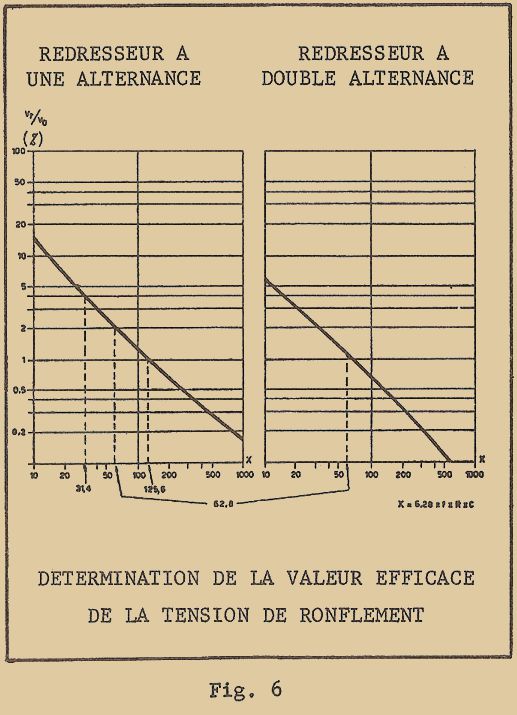
Pour une fréquence de 50 Hz, une capacité de 0,0004 F (=400 µF) et une résistance de 500Ω, on obtient :

X = 6,28 x 50 x 0,0004 x 500 = 6,28 x 0,02 x 500 = 6,28 x 10 = 62,8

En reportant cette valeur sur l’axe horizontal du graphique, on déterminera la valeur de la tension de ronflement, en pourcent par rapport à la tension continue de sortie. Dans l’exemple, la tension de ronflement est égal à 2% (environ) de la tension Vo qui alimente la charge.

Si l’on augmente la capacité du condensateur, on peut diminuer la valeur de la tension de ronflement.Ainsi, si l’on prend un condensateur de 800 µF, à la place de 400 µF, la valeur de X est doublée (125,6 au lieu de 62,8) et on trouve que la tension de ronflement n’est plus que de 1% environ.

Inversement, si la résistance de charge diminue, c’est-à-dire que le courant délivré par le redtresseur augmente, la valeur de la tension de ronflement augmente. Ainsi, si le courant délivré est doublé (lorsque la résistance de charge est deux fois plus faible) la valeur de X est divisée par 2 (31,4 au lieu de 62,8) ; la tension de ronflement passe de 2% à 4% environ.

Une caractéristique importante de la diode est la valeur maximum I_DM du courant direct. Dans le cas du redresseur à charge capacitive et résistive, la valeur de crête du courant redressé (pour une valeur égale de la tension moyenne), augmente notablement ; on doit donc réduire le courant moyen redressé de façon que le courant de crête dans la diode ne dépasse la valeur maximum admissible. Il peut aussi arriver que le courant continu maximum que l’on peut obtenir avec un circuit déterminé soit limité par la valeur I_DM ou bien que la limitation provienne de la tension inverse maximum –V_DpM.

Les deux limitations ne sont pas indépendantes ; de plus, il faut encore tenir compte de l’échauffement de la diode, produit par le passage du courant direct et inverse. Par effet de cet échauffement, les deux valeurs –V_DpM et I_DM subissent des réductions sensibles ; il faut donc en tenir compte aussi dans le calcul du courant continu maximum que l’on doit admettre dans la charge.

En pratique, pour utiliser correctement la diode dans un circuit redresseur il convient de considérer la caractéristique de charge qui représente l’allure de la tension continue (V_o) en fonction du courant continu délivré (I_o).

La caractéristique de charge est donné par le constructeur pour un circuit d’utilisation type. Elle permet d’établir immédiatement la valeur maximum de la tension d’entrée que l’on peut appliquer au circuit, la valeur maximum du courant moyen redressé, la chute de tension qui se produit aux bornes de la diode et la résistance de protection Rt qu’il faut utiliser pour toute valeur du courant délivré. Ainsi, par un simple calcul basé sur la loi d’ohm, on peut déterminer rapidement la résistance de charge minimum admissible.

Je vous ai reporté en figure 7, le schéma d’un redresseur à une alternance et la caractéristique de charge qui s’y rapporte.

La diode utilisée est une OA 214 ; elle admet une tension inverse maximum (-V_DpM) de 700 V et un courant redressé maximum (I_o) de 500mA.

La valeur de I_o peut être vérifiée immédiatement en lisant la valeur maximum reportée sur l’axe horizontal (500mA)

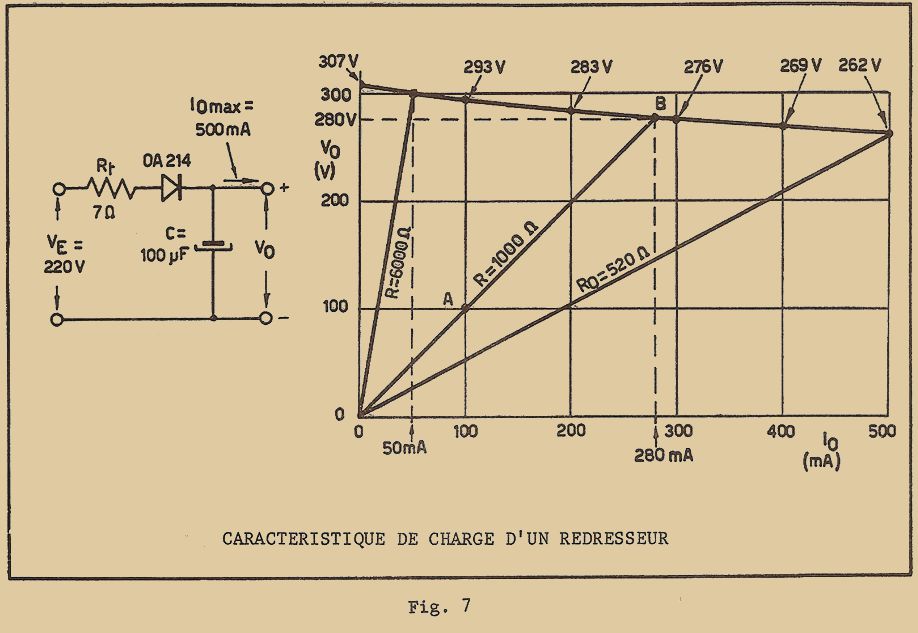
D’autre part, sur l’axe vertical, on peut lire la valeur de la tension maximum présente à la sortie (307 V) quand le redresseur fonctionne à vide.

En doublant cette valeur (2 x 307 = 614 V) on trouve que la valeur de la tension inverse maximum appliquée à la diode est nettement inférieure aux 700 V (= -V_DpM) qu’indique le constructeur de la diode. Je signale que 307V correspond à peu de chose près à la valeur de crête d’une tension secteur de 200 V_eff .

Il est intéressant de calculer maintenant la valeur de la résistance de charge qui correspond à un courant délivré I_o.

Pour cela, il suffit d’appliquer la formule R = V/I (loi d’ohm).

Par exemple, si I_o = 0,05 A (= 50mA) et Vo = 300 V, la résistance de charge sera :

R = 300/0,05 = 6000Ω

On déterminerait de la même manière que dans le circuit de la figure 7, la résistance de charge minimum que l’on peut admettre et qui correspondrait à un courant I_o maximum, est égale à 520Ω environ.

Inversement, si l’on connait la valeur de la résistance de charge, on peut déterminer directement sur le graphique la valeur de la tension et du courant de sortie.

Pour tracer la droite de charge R, il suffit de déterminer un seul point et de joindre celui-ci à l’origine 0 du système d’axes.

Ainsi, si R = 1000Ω, on détermine le point A de la droite de charge qui représente R, en se fixant par exemple la tension V = 100 V et en calculant le courant qui y correspondrait.

I = V/R = 100/1000 = 0,1 A = 100mA

Ayant déterminé le point A (qui appartient obligatoirement à la droite de charge), il suffit de le joindre à l’origine 0 et de prolonger la droite jusqu’à son intersection B avec la caractéristique.

Les valeurs qui correspondent au point B indiquent respectivement la tension de sortie (Vo = 280 V) et le courant de sortie (I_o = 280mA) qui alimentent la charge de 1000Ω.

En examinant la caractéristique d’un redresseur, il est important de remarquer comment varie l’allure de la tension de sortie lorsque le courant absorbé par la charge augmente.

En passant de 0 à 100mA, la chute de tension est de 14 V ; de 100mA à 200mA, la chute de tension est de 10 V ; de 200 à 300mA, elle est de 7 V ; de 300 à 400, puis de 400 à 500mA, elle reste à 7 V.

En comparant ces valeurs, on voit immédiatement que la chute de tension est plus importante dans le début de la caractéristique ; ceci est dû à la courbure de la caractéristique de la diode ; on a donc une résistance dynamique plus grande lorsque l’on travaille avec des tensions directes proches de la valeur du seuil. Plus loin, la chute de tension diminue et tend à se stabiliser à une valeur de 7 V pour chaque intervalle de 100mA.

La variation de la tension de sortie en fonction de la charge peut être indésirable si l’on désire alimenter un circuit à tension constante. On est souvent obligé de recourir à des systèmes particuliers de stabilisation qui réduisent ces variations à des limites fixées à l’avance.

Dans la prochaine et dernière leçon, nous étudierons les circuits redresseurs à double alternance, les doubleurs de tension et le circuit fondamental de stabilisation des tensions par utilisation des propriétés des diodes Zener.

---

EXERCICES DE RÉVISION SUR LA 29^ème LEÇON THÉORIQUE

1 – Comment calcule-t-on la valeur maximum de la tension inverse appliquée à une diode redresseuse à charge purement capacitive (ou à capacité et résistance), lorsque l’on connait la valeur de crête de la tension à l’entrée ?

2 – Quelle est la valeur maximum de la tension inverse appliquée à une diode redresseuse à charge purement capacitive, lorsque la tension à l’entrée est donnée en volts efficaces ?

3 – Qu’appelle-t-on tension de seuil d’une diode ?

4 – Lorsque l’on connait la valeur maximum admissible (-V_DpM) de la tension inverse d’une diode, comment peut-on calculer la valeur efficace de la tension maximum d’entrée V_EM ?

5 – Lorsque l’on diminue la résistance de charge d’un redresseur, est-ce que la tension de ronflement diminue aussi ?

6 – On désire obtenir un taux de ronflement de 1% (redresseur à une seule alternance). Quelle est la capacité que l’on doit utiliser si la résistance de charge est 1000Ω (secteur à 50 Hz) ?

7 – Quelle est la tension de ronflement dans le circuit précédent, si la tension de sortie est 250 V ?

8 – En utilisant le graphique de la figure 7, déterminer le courant I_o et la tension Vo pour une charge de 667Ω ?

9 – Est-ce que la tension de sortie d’un redresseur dépend du courant qui alimente la charge ?

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 28^ème LEÇON THÉORIQUE

1 – La contre-réaction diminue le gain d’un amplificateur.

2 – La contre-réaction est encore appelée Réaction négative. La réaction positive, rappelons-le, est utilisée dans les oscillateurs.

3 – Les principaux avantages de la contre-réaction sont : réduction des distorsions introduites par l’amplificateur et extension de la bande de fréquence.

4 – Le degré de contre-réaction indique de combien de fois est réduit le gain de l’amplificateur contre-réactionné par rapport au gain qu’il présenterait en l’absence de contre-réaction

5 – Il suffit d’appliquer la formule :

D = 1 + (b x G)

où D = 10 et G = 1000

d’où D – 1 = b x G

et b = (D-1)/G = (10-1)/1000  = 9/1000

6 – Le degré de contre-réaction est D = 5

Le gain de l’amplificateur avec contre réaction est :

G’ = G/(D ) = 80/5 = 16

La distorsion est maintenant réduite à (5%)/5 = 1%

La bande passante s’étend de 10 Hz à 50.000 Hz

7 – La pile sèche est constituée en général par deux électrodes (une positive et une négative) par un électrolyte, par un matériau absorbant qui sert à immobiliser l’électrolyte, par un matériau dépolarisant et par un bac enveloppe.

8 – Les accumulateurs se distinguent des batteries primaires par les matériaux qui les composent, par les transformations chimiques qui s’y produisent et par le fait qu’ils peuvent être rechargés en les reliant à un générateur approprié de courant continu.

9 – Une batterie solaire est constituée par un certain nombre d’éléments reliés entr’eux en série, ou en parallèle, ou en série-parallèle ; chaque élément est formé par une simple jonction PN que l’on expose aux radiations solaires.

Fin de la leçon 29

---

LECON 30

REDRESSEURS DOUBLE ALTERNANCE
MULTIPLICATEURS DE TENSION

Je vous donne en figure 1, les schémas de principe des redresseurs les plus courants et qui dérivent du redresseur à une seule alternance, étudié dans la dernière leçon.

Il s’agit ici de circuits classiques, très largement utilisés dans les montages à tubes.

Le montage de la figure 1a est constitué par deux circuits identiques et semblables à celui de la figure 1a de la précédente leçon théorique. Ces deux circuits ont en commun la charge (représentée par le condensateur C) et la résistance de protection R_t.

Si l’on se rappelle que lorsque la tension V_E est positive sur D1, elle est alors négative simultanément sur D2 (et inversement), on voit immédiatement que pendant une alternance c’est D1 qui travaille et D2 est bloquée, et que pendant l’alternance suivante, c’est D2 qui conduit et D1 est bloquée.

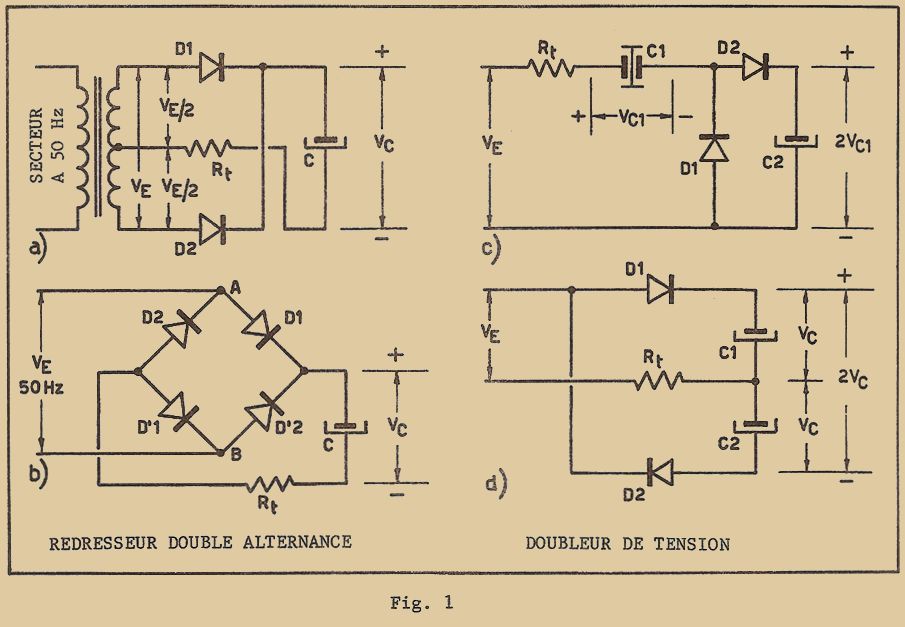
Nous dirons en d’autres termes, que l’onde entière est appliquée à la charge, la moitié au travers de D1 et l’autre moitié au travers de D2.

Il faut encore préciser qu’à chacune des diodes est appliquée non pas toute la tension V_E, mais seulement V_E/2 qui apparait entre la prise centrale et les extrémités du secondaire du transformateur. En conséquence, la tension de sortie VC qui en résulte est diminuée elle aussi par rapport à celle que l’on pourrait obtenir avec la même tension V_E que l’on appliquerait à une seule diode. L’avantage de ce circuit réside en une réduction sensible de la tension de ronflement dans des mêmes conditions de charge, comme vous pouvez le constater en examinant les graphiques de la figure 6, Théorique 29. En effet, pour la même valeur de X, c’est-à-dire pour la même fréquence et la même constante de temps de la charge (par exemple pour R x C = 62,8) on trouve que le pourcentage de la tension de ronflement a été diminué de moitié et est passé de 2% à 1% environ.

Le circuit en pont de la figure 1b est analogue au précédent et accomplit les mêmes fonctions et donne les mêmes résultats en ce qui concerne la tension de ronflement. Le principal avantage de ce circuit, consiste dans la possibilité de le brancher directement sur le secteur et éliminer ainsi le transformateur d’alimentation, puisque l’on n’a plus besoin d’avoir un secondaire à prise médiane.

Quand le point A du circuit est positif et B négatif, l’alternance positive de V_E traverse les diodes D1 et D’1 car elles se trouvent polarisées, en sens direct. Inversement quand le point A est négatif et B positif, l’alternance négative de V_E traverse les diodes D2 et D’2.

La tension d’entrée V_E, se répartit toujours aux bornes de deux diodes reliées en série : ainsi, la tension inverse maximum que l’on peut appliquer est égale à la somme des tensions inverses maxima que peut supporter chacune des diodes. Ceci constitue donc un avantage en ce sens que l’on peut utiliser des diodes moins chères et compenser ainsi en partie, la dépense supplémentaire occasionnée par D’1 et D’2. En pratique, les quatre diodes du redresseur en pont sont vendues déjà reliées et enfermées dans une enveloppe de protection (qui fait office aussi d’ailette de refroidissement).

De cette façon, on réalise une diminution du coût de fabrication.

Les figures 1c et 1d représentent les schémas de deux redresseurs-multiplicateurs de tension.

Les capacité C1 du circuit de la figure 1c est obtenue en reliant en série (sortie positve avec sortie négative) deux condensateurs électrochimiques ; on évite ainsi que les électrochimiques ne soient détruits par le passage du courant alternatif et on obtient en même temps, une capacité plus grande que celle de deux condensateurs au papier et qui serait insuffisante.

Supposons qu’initialement C1 soit déchargé et que la tension V_E soit négative du côté R_t – C1. Dans ces conditions, la diode D1 est polarisée dans le sens direct et le condensateur C1 se charge à la valeur de crête Vc1. Pendant l’alternance positive, c’est la diode D2 qui se trouve être polarisée dans le sens direct, tandis que D1 est maintenant bloqué. La tension Vc1 s’ajoute à la tension V_E, de façon que la valeur de crëte de la tension directe qui se trouve appliquée à D2 soit double de celle de la tension du secteur appliquée à D1 : de cette façon, le condensateur C2 se charge à la tension 2 Vc1.

Le circuit de la figure 1d est légèrement différent quoique le but à atteindre (doubler la tension de sortie Vc) reste le même.

Dans ce circuit, les deux diodes travaillent alternativement : D1 pendant l’alternance positive de V_E et D2 pendant l’alternance négative. Le condensateur C1 se charge à la même valeur de crête Vc au travers de la diode D1 ; de même C2 se charge à la même valeur de crête Vc au travers de la diode D2 ; ainsi la tension à la sortie, qui est donnée par la mise en série des deux tensions Vc, est égale à 2 V_c.

Les doubleurs de tension du type de ceux que je viens de vous décrire sont surtout utilisés dans les alimentations des téléviseurs.

Ils sont surtout avantageux du fait qu’ils permettent d’éliminer un transformateur et de réduire aussi poids, encombrement et prix.

Je vous donne en figure 2 les principales caractéristiques moyennes sur les redresseurs d’utilisation courante.

En comparant les valeurs admissibles en densités de courant, on voit que la diode au silicium offre des possibilités plus grandes par rapport à n’importe quelle autre diode à semi-conducteur, tandis que celles à oxyde de cuivre ne peut être utilisée que pour alimenter des appareils qui n’absorbent que peu de courant (comme par exemple un contrôleur universel).

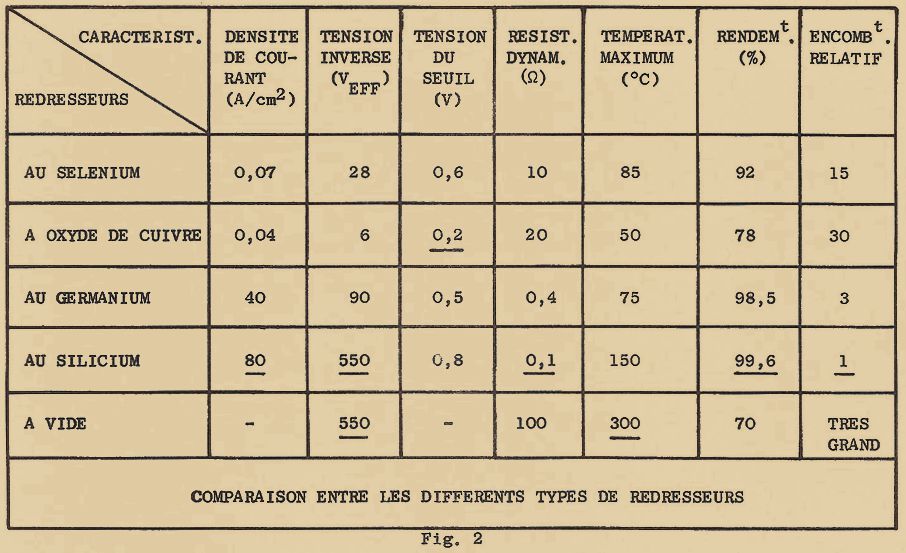
Comme vous pouvez le voir d’après ce tableau, la diode au silicium est supérieure ou tout au moins égale par rapport à toutes les autres diodes, en ce qui concerne la tension inverse admissible, le rendement maximum, la résistance dynamique minimum, l’encombrement minimum à puissance égale. Elle est supérieure aux autres diodes à semi-conducteur en ce qui concerne la température maximum admissible.

On peut donc prévoir facilement une diffusion de plus en plus grande de la diode au silicium en remplacement ses tubes redresseurs classiques et même des autres redresseurs, spécialement ceux au silicium et au germanium.

Les diodes à l’oxyde de cuivre continuent à être utilisées dans les appareils qui nécessitent une faible tension d’alimentation (et un faible courant), mais qui ont besoin d’une faible tension de seuil. Les diodes sont d’ailleurs bon marché.

2 – STABILISATION DE TENSION A DIODE ZENER (ET A TRANSISTORS)

Nous avons vu dans la 6ème leçon théorique que l’allure de la caractéristique inverse d’une diode à jonction se modifiait notablement quand la tension inverse qu’on lui appliquait, dépassait une certaine valeur (V_Z), même de quelques dizièmes de volt ; il suffit d’un très léger accroissement de V_Z pour déterminer une augmentation très sensible du courant inverse ; ainsi la caractéristique tension-courant prend une allure presque verticale, pendant que V_Z reste presque horizontal.

La figure 3 représente l’allure typique de la caractéristique d’une diode au-delà du point de Zener.

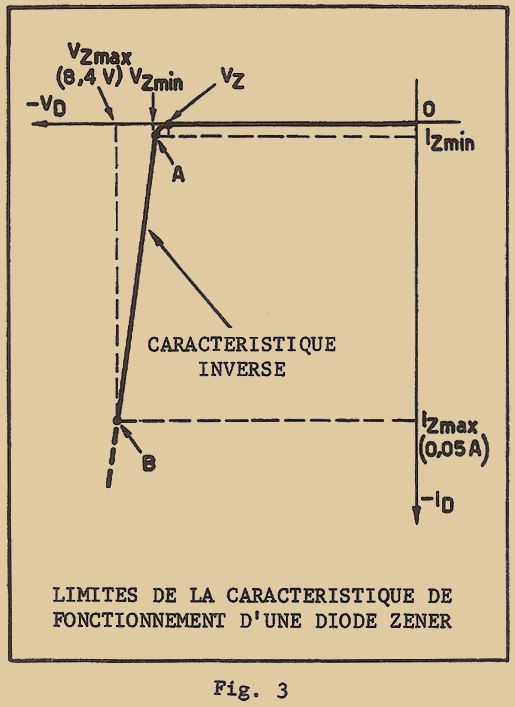
Vous remarquerez, que la courbe comprise entre les points A et B n’est pas verticale, mais qu’elle est inclinée sur l’axe –V_D (d’ailleurs plus que ne l’est en réalité la caractéristique d’une diode Zener) : ceci a été fait pour bien montrer l’intervalle entre V_Zmax et V_Zmin où doit fonctionner normalement la diode Zener.

La tension V_Z indique le point où commence à se manifester le phénomène de Zener. Entre V_Z et V_Zmin, la courbe présente un coude où l’on note le passage progressif d’une résistance inverse très grande (de l’ordre du mégohm) à une résistance très faible (de quelques ohms).

Les diodes redresseuses que nous avons vues précédemment ne peuvent en général fonctionner à la tension V_Z qui représente la limite maximum absolue de la tension inverse. Elles ne peuvent non plus fonctionner à des tensions inverses supérieures, car le courant I_Z qui traverserait alors la diode détruirait irrémédiablement la jonction. Les diodes Zener par contre, sont réalisées, pour fonctionner à des tensions supérieures à V_Z, C’est-à-dire dans la région rectiligne de la caractéristique comprise entre les points A et B (figure 3). Pour des tensions inverses inférieures à V_Z et pour les tensions directes, leur caractéristique est semblable à celle des redresseurs.

Les diodes Zener sont obtenues par un procédé d’alliage entre une plaquette de silicium N et un fil d’aluminium. On obtient ainsi une jonction PN ayant toutes les propriétés d’une jonction redresseuse, mais dans laquelle le phénomène de Zener apparait pour des tensions V_Z relativement faibles (pour quelques volts à quelques dizaines de volts).

Comme semi-conducteur, on utilise du silicium, étant donné qu’avec ce dernier, on peut atteindre des températures relativement élevées (150°C) c’est-à-dire supérieures à celles que l’on peut obtenir dans les jonctions par effet du courant important de Zener.

Pendant le montage, la diode est enfermée d’une façon hermétique dans une enveloppe métallique de quelques millimètres de diamètre ; cette enveloppe, outre son rôle d’offrir une grande robustesse, permet de dissiper toute la chaleur qui se forme dans la jonction pendant le fonctionnement au-delà du point Zener.

Pour cette raison le constructeur indique dans ses données techniques la valeur de la puissance maximum à ne pas dépasser. Ainsi, lorsque l’on s’est fixé le point B (figure 3), c’est-à-dire le point de fonctionnement correspondant à la tension maximum appliquée (V_Zmax) faut-il encore vérifier sur le graphique de la caractéristique, la valeur du courant maximum I_Zmax et calculer que le produit V_Zmax x I_Zmax ne dépasse pas la puissance maximum que l’on peut dissiper.

Si par exemple, la puissance maximum que l’on peut dissiper à 25°C, est 0,5W, que la tension maximum inverse appliquée est de 8,4 V et que I_Zmax, (lu sur le graphique de la caractéristique de la diode) correspondant est de 50mA (0,05A), la puissance est :

V_Zmax x I_Zmax = 8,4 x 0,05 = 0,42 W

La valeur ainsi trouvée (0,42 W) ne dépasse pas la valeur maximum indiquée (0,5W) ; le point de fonctionnement prévu est donc correct.

Outre le point B, il faut encore déterminer sur la caractéristique, le point A, qui délimite la région rectiligne au voisinage du coude. En effet, à partir du point A et jusqu’au point 0, les variations de tension ne correspondent pas à de grandes variations du courant, et comme nous le verrons plus tard, on perd le bénéfice de l’effet stabilisateur de la diode dans les circuits de régulation.

En général, au point A correspond une tension minimum V_Zmin, qui est supérieure de quelques dizièmes de volts à la tension de Zener V_Z et pour lequel, le courant I_Zmin est de quelques dizièmes de milliampères.

Les limites que nous venons de voir, V_Zmax et I_Zmax (qui sont déterminées en fonction de la puissance maximum et que l’on peut dissiper) et V_Zmin et I_Zmin (qui sont déterminées en considérant sur la caractéristique le point extrème A dans la région rectiligne au-delà du point de Zener, sont très importantes pour étudier le fonctionnement des circuits classiques de régulation qui constituent les applications principales des diodes Zener.

Je vous ai dessiné en figure 4, le schéma de principe d’un régulateur de tension avec diode Zener.

En série avec la diode D_Z, figure la résistance R_d qui représente la résistance dynamique de cette même diode, c’est-à-dire la résistance qui est offerte au passage du courant I_Z, quand ce dernier varie dans les conditions normales de fonctionnement entre I_Zmax et I_Zmin.

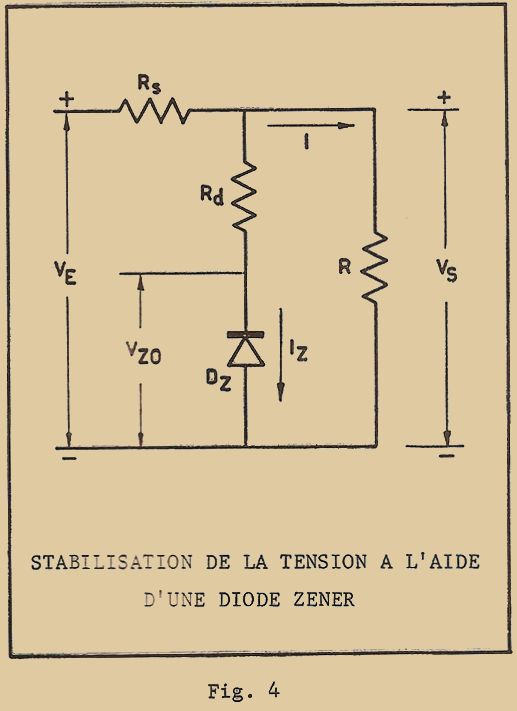
La résistance dynamique d’une diode Zener qui travaille comme stabilisatrice de tension, est de l’ordre de quelques ohms. D’autre part, la tension V_Zo, présente aux bornes de la diode quand le courant I_Z est presque nul, est de l’ordre de quelques volts à quelques dizaines de volts.

Etudions par exemple la variation de V_S en supposant que R_d = 2 Ω

et que : I_Zmin = 2mA ; I_Zmax = 30mA ; V_Zo = 8 V

Avec ces données, nous pouvons calculer la valeur de V_S en tenant compte de la relation : V_S = V_Zo + (I_Z x R_d)

dans laquelle le produit I_Z x R_d représente la chute de tension aux bornes de la diode dûe à la résistance dynamique R_d.

Pour I_Zmin = 2mA = 0,002A et I_Zmax = 30mA = 0,030 A on obtient respectivement les valeurs suivantes :

V'_S = 8 + 0,002 x 2 = 8,004 V

V''_S = 8 + 0,03 x 2 = 8,06 V

En effectuant la différence entre les valeurs ainsi trouvées :

V''_S - V'_S = 8,060 – 8,004 = 0,056 V

on détermine la variation maximum de la tension V_S correspondant à une variation du courant I_Z de 2mA à 30mA. On peut voir rapidement que cette variation de la tension est très faible par rapport à la valeur de la tension présente initialement aux bornes de la diode. En effet, la variation de 0,056 V par rapport à 8,004 représente une variation inférieure à 1% de la tension disponible (pour une variation du courant très grande).

La diode Zener du circuit stabilisé de la figure 4 se comporte un peu comme une soupape de sécurité dans une enveloppe où existe une certaine pression. Quand la tension à l’entrée V_E augmente, la tension V_S tend à augmenter aussi : Le courant absorbé par la charge tend à augmenter aussi. Mais c’est à ce moment qu’intervient la diode : à un accroissement de V_S, elle absorbe un courant I_Z plus grand qu’initialement ; une chute de tension plus grande aux bornes de R_S se produit et s’oppose ainsi à l’accroissement de V_E ; la valeur de la tension de sortie V_S reste ainsi pratiquement inaltérée.

On obtient des résultats semblables à ceux où la tension de sortie est stabilisée, si c’est le courant I dans la charge qui varie.

En effet, si le courant I diminue, la chute de tension aux bornes de la résistance R_S diminue aussi et la tension V_S tend à augmenter ; mais comme on l’a vu, à un accroissement de V_S correspond un accroissement sensible de I_Z qui compense la diminution du courant absorbé par la charge et maintient ainsi constante la chute de tension aux bornes de R_S et donc la tension de sortie V_S.

Si maintenant, au lieu de considérer un accroissement de la tension d’entrée V_E, ou une diminution du courant absorbé par la charge, on considère une diminution de V_E (ou bien un accroissement de I), on retrouve le même effet de stabilisation, avec comme seule différence que la tension V_S tend maintenant à diminuer et provoque ainsi une notable diminution de V_E et d’un autre côté peut compenser l’accroissement de I.

Soit que l’on considère la variation de la tension d’entrée V_E, soit que l’on considère la variation du courant I absorbé par la charge, on voit le rôle primordial de la résistance R_S, qui est appelée résistance de stabilisation ou résistance de limitation. Chacune de ces deux dénominations met en évidence la fonction fondamentale de la résistance R_S et chacune d’entr’elles peut être mise en avant.

Comme résistance de stabilisation, R_S recueille toutes les variations du courant I_Z et du courant I (figure 4) ; ainsi, la chute de tension qui apparait à ses bornes, fait varier légèrement la tension V_S qui suit l’allure des deux courants et règle en même temps, le courant I_Z de la diode. Comme résistance de limitation, R_S sert à protéger la diode des surcharges en maintenant le courant I_Z entre les limites de la valeur maximum admissible (puissance dissipable maximum à ne pas dépasser).

Quand on utilise une diode Zener pour stabiliser une tension d’alimentation ou pour délivrer une tension constante de référence (comme nous le verrons tout à l’heure) : faut-il encore choisir pour une tension d’entrée V_E donnée, la valeur appropriée de R_S.

De R_S, dépend en premier lieu, le facteur de "variation". C’est le rapport entre la variation de la tension d’entrée que l’on désire stabiliser et la variation résiduelle de la tension de sortie stabilisée. On démontre, qu’il existe entre ces différentes grandeurs, la relation suivante :

(Variation de V_E)/(Variation de V_S ) = 1 + R_S/R_d

Ainsi, en connaissant la résistance dynamique (R_d) de la diode au point de fonctionnement prévu, en connaissant aussi la variation maximum de V_E à l’entrée et les variations de V_S stabilisée que l’on peut accepter, on pourra calculer facilement la valeur correspondante de R_S. Avant d’aller plus loin il faut faire quelques remarques.

La relation précédente est seulement valable, si l’on considère que le courant I absorbé par la charge reste constant. La relation ne définit donc pas totalement la "qualité" du circuit stabilisé.

Ainsi, pour mieux définir le circuit, on fait appel à un autre facteur, appelé Facteur de stabilisation S qui peut être traduit par la relation suivante :

S = (1 + R_S/R_d ) x V_S/V_E

En comparant cette relation avec la précédente, on remarquera tout de suite que S dépend du facteur de "Variation", de la tension d’entrée V_E et de la tesion de sortie V_S. On peut démontrer aussi, que ce facteur n’est autre que le rapport entre la variation en pourcent de la tension d’entrée à la variation en pourcent de la tension de sortie stabilisée.

La valeur de S croît avec l’augmentation de R_S jusqu’à atteindre une valeur maximum, à partir de laquelle, un accroissement ultérieur de R_S reste pratiquement inefficace. On peut donc en conclure, que pour obtenir une bonne stabilisation, il faut que R_S soit suffisament élevée pour faire "sentir" son efficacité, c’est-à-dire qu’il faut que R_S soit très grande par rapport à R_d ; mais il ne faut pas non plus que R_S soit infiniment grande, parce qu’à partir d’un certain point, son efficacité pratique serait presque négligeable. Son efficacité pourrait même devenir néfaste, si à cause de la chute de tension aux bornes de R_S, la diode se trouvait à travailler en deçà du point A (figure 3), c’est-à-dire dans le coude de la caractéristique au lieu de la région rectiligne comprise entre les points A et B.

En pratique, pour trouver la valeur appropriée de R_S, on commence par déterminer tout d’abord la valeur minimum I_Zmin du courant dans la diode, de façon que pour cette valeur de courant, le point de fonctionnement se trouve au-delà du coude de la caractéristique (figure 3). Ensuite, en connaissant la tension minimum à l’entrée (V_Emin), la tension de Zener (V_S) et le courant maximum dans la charge (I_max) on calcule R_S à l’aide de la formule :

R_S = (V_Emin-V_S)/(I_Zmin+ I_max )

Par exemple, pour V_Emin = 36 V, V_S = 24V, I_Zmin = 0,002 A et I_max = 0,05A, on trouve :

R_S = (36-24)/(0,002+0,05) = 12/0,052 = 230 Ω

De cette façon, on peut déterminer la valeur maximum de la résistance de stabilisation pour protéger efficacement la diode et de façon que pour cette valeur l’effet négatif dû à la courbure de la caractéristique au voisinage du point de Zener ne se fasse pas encore sentir.

Le circuit régulateur de la figure 4 est prévu pour des montages à faible ou moyenne puissance ; pour des puissances plus élevées, la stabilisation ne peut être meilleure que 5%. Pour obtenir des stabilisations meilleures à de faibles tensions et de forts courants, on utilise les diodes Zener comme éléments qui délivrent des tensions de référence dans des circuits à transistors (ou à tubes).

En figure 5, je vous ai reporté deux schémas de principe qui illustrent l’utilisation des diodes Zener dans des circuits stabilisés à transistors.

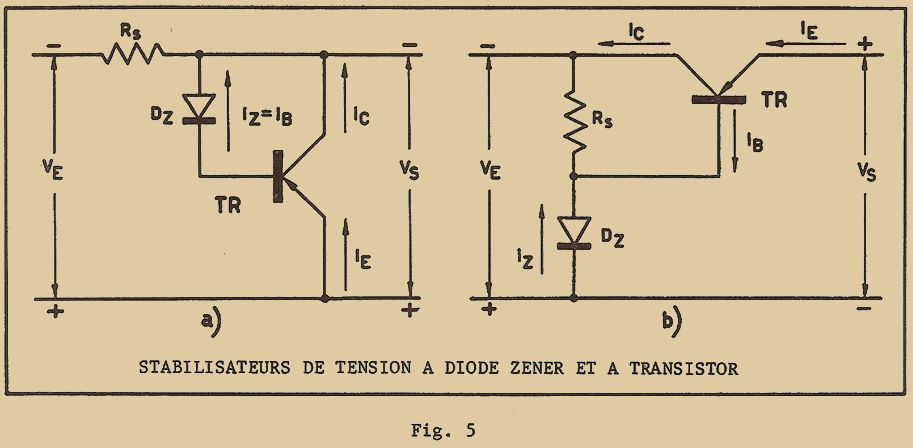
La figure 5a représente un circuit simple qui utilise un transistor de puissance comme élément stabilisateur placé en parallèle sur la charge. La tension de collecteur est prélevée à la sortie du régulateur constitué par la diode D_Z, la résistance de limitation R_S et par la résistance directe de la diode émetteur-base du transistor TR.

L’effet stabilisateur est accru par la présence du transistor. En effet, supposons que le courant I_Z augmente par suite d’un accroissement de la tension d’entrée V_E. Ceci va se traduire par un accroissement du courant de base (I_Z = I_B) qui va entraîner une augmentation du courant de collecteur I_C. Ceci va correspondre en définitive à une chute de tension plus grande aux bornes de R_S qui tendra à s’opposer à l’accroissement initial de V_E. Le mécanisme de la stabilisation est encore le même que dans le circuit de la figure 4, avec la seule différence que la stabilisation est beaucoup plus énergique en ce sens que les variations du courant I_Z (déjà assez importantes par elles-mêmes) sont ici encore plus grandes puisqu’elles sont amplifiées par le transistor.

Le montage de la figure 5b, à la différence du précédent, utilise le transistor stabilisateur en série avec la charge, et tout le courant d’émetteur I_E traverse la charge.

Dans ce circuit, la diode Zener sert à stabiliser la tension de base de façon à ce que le courant I_E (et par conséquent la tension V_S) reste constant malgré les variations possibles de la tension d’entrée V_E.

Avec les circuits simples dérivés directement de ceux de la figure 5 on peut obtenir des stabilisations meilleures que 2% pour des basses tensions et de forts courants ; en augmentant le nombre de transistors, c’est-à-dire en rendant plus complexes les circuits, mais en se basant toujours sur les mêmes principes, on peut obtenir des stabilisations de l’ordre de 1% ou même moins.

---

EXERCICES DE RÉVISION SUR LA 30^ème LEÇON THÉORIQUE

1 – Parmi les différentes diodes à semi-conducteurs, quelle est la meilleure à utiliser en tant que redresseur ?

2 – Dans quels appareils utilise-t-on le redresseur à oxyde de cuivre à faible courant ?

3 – Si on devait utiliser un redresseur à une température de 200°C quelle sorte de diode faudrait-il choisir ?

4 – Dans quelle région de la caractéristique, doit-on faire travailler la diode Zener en stabilisatrice de tension ?

5 – Qu’appelle-t-on "facteur de variation" ?

6 – Comment définit-on le "facteur de stabilisation" S d’un régulateur simple à diode Zener ?

7 – Comment calcule-t-on la résistance de stabilisation R_S dans un régulateur simple à diode Zener ?

8 – Quel est l’avantage dans l’utilisation d’un transistor associé à une diode Zener dans un régulateur plus complexe ?

9 – Quel est l’ordre de grandeur de la résistance dynamique d’une diode Zener au point de fonctionnement ?

---

RÉPONSES AUX EXERCICES DE RÉVISION SUR LA 29^ème LEÇON THÉORIQUE

1 – La valeur maximum de la tension inverse qui se trouve appliquée à une diode à charge capacitive (ou à résistance et capacité) est égale à la valeur de crête à crête (V_pp) de la tension d’entrée ; ainsi, en connaissant la valeur de crête (V_p) de la tension d’entrée, on calcule la valeur maximum de la tension inverse en multipliant par 2 cette valeur (V_pp = 2 V_p)

2 – Si la tension à l’entrée est donnée en volts efficaces, il faut la multiplier par 2,82 pour obtenir la valeur crête-crête :

(V_pp = 2,82 V_eff)

3 – La tension de seuil d’une diode est la valeur maximum de la tension directe pour laquelle le rendement du redresseur est encore pratiquement égal à zéro

4 – La valeur efficace de la tension d’entrée maximum que l’on peut admettre est donnée par

V_EM = -V_DM/2,82

5 – Non ; en diminuant la résistance de charge, la tension de ronflement augmente.

6 – En reprenant la figure 6 (Théorique 29) on voit que pour 1% de ronflement X = 125,6.

Comme X = 6,28 x f x C x R

On trouve C= 125,6/(6,28 x 50 x 1000) = 0,0004F (= 400µF)

7 – Le taux de ronflement étant de 1% nous avons :

t = 1/100 = V_r/V_o  d’où V_r = V_o/100 = 250/100 = 2,5V

8 – Déterminons un point A’ de la droite de charge en prenant par exemple un courant de 300mA. La tension est alors V = RI = 666 x 0,3 = 200 V (environ). Joignons le point A’ à l’origine 0. Prolongeons cette droite qui coupe la caractéristique au point B’. La valeur du courant est 400mA (environ) et la tension est 269V (environ)

9 – Oui ; la tension de sortie d’un redresseur diminue lorsque le courant absorbé par la charge augmente, à cause de la chute de tension qui se produit aux bornes : de la résistance interne de la diode, de la résistance de protection et de la résistance du transformateur (ou aux bornes de la résistance interne du générateur).

Fin de la leçon 30

---